航空发动机叶片自适应磨抛定量去除研究*

王 辉，赵 欢，罗来臻

(华中科技大学数字制造装备与技术国家重点实验室，武汉 430074)

0 引言

航空发动机叶片是航空发动机内部的核心零部件之一，其在航空发动机内部种类多、数量大且关系着航空发动机的工作性能与寿命。航空发动机叶片的工作环境复杂、温度高、压强大，风速快[1]。叶片加工后的尺寸与形状达不到理论设计的要求，则可能导致航空发动机出现影响发动机工作性能的现象[1-2]，如失速、气喘和紊流等，甚至在非常严重时影响到飞行的安全性，因此在加工制造时必须保证加工后的发动机叶片具有严格的型面完整性以及精度很高的截面尺寸[1]。

目前工业上对所有批次叶片采用相同的磨抛工艺参数对叶片进行磨抛，可能会导致叶片某些部位出现过磨或者欠磨的情况。针对该问题，工业界提出自适应加工的概念[3-5]，通过加工前的测量数据，对特定叶片的加工工艺进行修调。

自适应加工主要分为两种，一类是尺寸自适应，一类是形状自适应。尺寸自适应主要通过修调磨抛过程中的工艺参数，对叶片型面轮廓度进行控制；形状自适应主要通过修调磨抛刀路，对叶片形状进行控制。本文主要按以下思路对尺寸自适应进行研究：首先根据测量数据进行叶片表面的余量计算与分析，与此同时可以在前期试验中，构建该叶片材料的去除率模型，利用该先验的材料去除率模型，对已经规划好的刀路点进行工艺参数规划。

1 NURBS曲面重构

1.1 NURBS曲线曲面概述

采用有理多项式与基函数表达m次NURBS曲线[6]时，曲线方程的表达式如式(1)所示。

(1)

式中，m为曲线的次数；p为曲线的控制顶点；w为曲线的控制顶点权因子；u为曲线方程参数值；Ni,m(u)是按照节点向量U构造的样条基函数。

B样条基函数是在每个节点向量U区间内建立的一种参数多项式，De-Boor Cox递推算法给出了m次规范B样条基函数的表达式如式(2)所示。

(2)

式中，i表示基函数的序号；m表示基函数的次数。

m×l次NURBS曲面的表达式如式(3)所示。

(3)

式中，u、v为两个方向的参数值，其他变量含义与式(1)中相应变量的含义相同。

1.2 NURBS样条曲线曲面重构方案

根据给定的型面数值点反求NURBS曲线的方法有拟合和插值，采用拟合的方式得到的曲线并不完全通过给定的型值点，而是通过给定的允许误差构造最逼近、最光顺的曲线[5-6]，这种方式通常应用于测量数据误差较大的情况；采用插值的方式得到的曲线完全通过给定的型值点，这种方式通常应用于测量数据精度很高的情况。本文采用高精度三坐标测量仪进行型值点的测量，测量精度高，因此选用插值的方式重构叶片表面。

本文在叶片截面内u向上采用二次NURBS曲线插值，且该曲线为闭曲线；在截面间v向上对每个截面相同节点控制区域的控制点采用三次NURBS曲线插值，该曲线为clamped曲线。

1.3 型值点参数化与节点向量的生成

(4)

(5)

式中，d为曲线的总弦长。

本文采用常用的平均节点向量的方式建立规范化的节点向量U，如式(6)所示。

(6)

当有n+1个数据点qi时，对数据点参数化之后可以得到n+2m+1个节点向量，可以反求出n+m个控制顶点。对clamped曲线，一般使首末节点的重复度为m+1，反求得到的控制顶点不重复，且首末控制顶点与曲线首末端点重合；而对闭曲线，则起始与末尾各m+1个节点的重复度为1，且u0-um与un-m-un、up+1-u2p与un+1-un+p+1之间的对应值相差1，得到的首末m个控制顶点重合。

1.4 构造系数矩阵与反求控制顶点

利用得到的参数点与节点向量可以利用n+1个型值点构造出n+3个控制点，因此在反算控制点时，需要额外添加两个边界约束条件。

(1)对于C1连续的二次闭曲线，边界条件为最后两个控制点及其支撑区间长度与初始的两个控制点及其支撑区间长度相同。根据控制顶点相同可以消除两个方程，再根据对应的支撑区间长度相同由此导致的首尾对应的基函数相等，可以作为补充的2个边界条件，如式(7)所示。根据式(5)、式(6)与生成的节点向量U可以得到反求控制顶点的方程如式(8)所示。

(7)

(8)

(2)对于三次clamped曲线，其边界条件可以使首尾的控制点与曲线的首尾端点重合，为了使插值曲线形状更加自由，数据点不作为曲线的首尾端点，在本文所处环境中，首末端点的切向不易获得，因此可以在首末局部根据式(9)作直线插值得到曲线的首尾端点。

(9)

式中，λ1、λ2是两个端点的延长比例系数，理论取值范围为(0,+∞)，为保证端点插值曲线形状误差较小，一般取值区间为[0.01,0.05]。

得到首末端点后，NURBS曲线的有效区间不再规范化，因此仍要重新生成数据点参数与节点向量。最后根据生成的节点向量V可以得到反求控制顶点的方程如式(10)所示。

(10)

2 叶片表面余量计算方法

2.1 与理论法线相交三角网格的寻找方法

用NURBS样条重构出的曲面为参数方程形式，而空间法线为三维直线方程，两组方程联立时很难得到解析解法，一般情况下只能通过数值解法进行求解，造成运算消耗过大，因此本文采用将参数化后的NURBS方程离散化的方式，将参数方程在有效定义域内等距采样，转化为三角网格形式。此时问题转化为空间之间与空间平面的求交问题，这样使得问题简化很多，本节主要介绍了寻找与法线相交的三角面片方法。

网格格式的表面数据，如式(11)所示。通常由空间点坐标P与由点序列构成的面片V两部分组成。

S={P={p0,…,pn},V={v0,…,vi}}

(11)

式中，n表示离散化后的点的数量；i表示离散点组成的三角面片的数量。

通常寻找三角面片的方式可以概括为如下步骤：先在P中寻找到与点q最近的测量重构表面上的离散点pj，在面片序列V中寻找包含pj的所有序列，判断该序列中是否包含与法线相交的三角面片，如果包含则寻找过程结束；如果不包含则重新在P中寻找与点q距离第二位的重构表面上的离散点pj*，重复上述过程，直至找到相交的三角面片。

判断直线是否与三角面片相交时，如果实际计算每一个平面与直线的交点，再判断交点是否在面片之内，这样的方法虽然很简单，但是遇到如图1所示的情况时，导致程序运算交点的运算过程较多，使得程序计算效率较低。

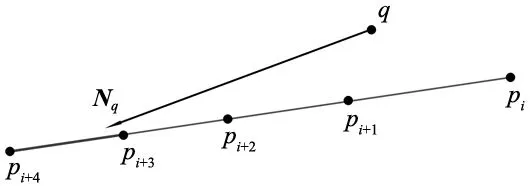
图1 求与直线相交的三角面片时的极端情况

本文采用一种快速判断直线是否与三角面片相交的方法，假设目前需要判断点q与面片v={pα,pβ,pγ}是否相交，构造面片三点与路径点的向量矩阵B，如式(12)所示。

B=[pα-q,pβ-q,pγ-q]

(12)

首先判断矩阵B是否为满秩，如果矩阵B不满秩，则点q在面片v所在的平面上，但不一定在面片v上，需要判断点q是否在三角形内部，此过程可参照有关书籍，本文不再叙述；如果矩阵B满秩，则点q与面片v不共面，此时将矩阵B的列向量视为一组斜空间坐标系的基向量，如图2所示，将点q的法向量Nq向基坐标系投影，为使判断求得的余量正负的简便，需在向基坐标系投影之前判定法向为表面朝外的方向，若投影值均为正，则该面片为所求的相交面片。

图2 判断直线与三角面片是否相交

为了减少判断直线与三角面片是否相交的次数，本文提出一种向单位球面投影点排序的寻找与直线相交的三角面片的加速算法。根据经验确定点q的K近邻内一般会出现与法线相交的三角面片的顶点，先取点q的K近邻点集为M，将点集M向以点q为球心的单位球面上投影，得到M的映射点集M′，如图3所示，将搜索中心点由点q变为q+Nq，再对点集M′内进行上述方法的遍历寻找，可以加快找到所求的三角面片的速度。该方法的优势是将所有的点映射到同一个尺度下进行寻找，这样可以避免由于点集P相对于点q的尺度不一致，导致的计算量的增加。

图3 向单位球面投影的加速算法示意图

2.2 沿空间直线方向的点到平面的距离公式

通过上节的方式，找到了与点q的法线Nq相交的三角面片v={pα,pβ,pγ}，接下来计算法线Nq与三角面片v的交点pacross与点q的距离λ。空间平面的三点式方程的形式较为复杂，且用该方程与空间直线求交的运算量也较大。因此，本文跳过求交点pacross的过程，通过向量关系，直接求解距离。

根据图4所示，先根据式(13)求三角面片v的法向量Nplane，并单位化，而余量向量pacross-q满足式(14)，点q到面片v上一点的向量可以构造为pα-q，将余量向量与点面向量投影到法向量Nplane，则两个向量的投影长度均为点q到面v的垂直距离，两个投影相等可以得到最终的加工余量λ，如式(15)所示。

图4 向量法计算直线上点到平面的直线方向距离

Nplane=(pβ-pα)×(pγ-pα)

(13)

pacross-q=λNq

(14)

λNq·Nplane=(pα-q)·Nplane

(15)

3 材料去除率模型建模

3.1 材料去除率模型概述

一种非线性的砂带磨削的数学模型被提出，该模型中材料的磨削去除量与工艺参数之间的关系是指数关系，在线性公式上进行了修改，使其更加符合真实加工场景[8-9]，其模型如式(16)所示。

(16)

式中，r为材料的去除量；KA为阻力系数；Vb为砂带的线速度；kt为砂带的磨损系数；Lw为砂带宽度；Vw为工件的进给速度；FA为系统施加在接触轮上的力。

崔一辉[9]综合考虑了砂带磨损因素、润滑条件、接触轮特征条件和温度因素，提出一种适用于砂带接触轮磨削的磨削量与加工参数的数学模型，如式(17)所示。

(17)

式中，A为匹配系数，与工件材料和砂带有关；pt、pc、pl分别为与温度有关的系数、与接触轮的特征相关的系数和与润滑有关的系数；Blife为砂带寿命系数；vr、vg为机器人进给速度与砂带线速度；Fb为法向磨削力；pB1、pB2为与磨削力相关的系数；pR1、pR2为与机器人进给速度相关的系数，且pR1为负数。

本文采用的实验平台为砂带力控磨抛机，因此可以采用上式进行本文的材料去除率建模，为了简化模型，本文只采用控制砂带线速度来控制去除量，因此式(16)和式(17)可以整合简化为式(18)所示。

(18)

3.2 材料去除率模型拟合

本节主要介绍利用上节中简化后的材料去除率模型，在恒力恒进给速度的情况下，对实验得到的材料去除量进行材料去除率模型的拟合。

采用最小二乘法对模型进行拟合，但是未知数中存在指数的情况，因此本文采用一种迭代求解的方法进行实数幂函数的拟合求解，给定迭代误差ε，迭代过程如图5所示。

图5 材料去除率拟合算法

4 叶片定量去除实验

4.1 表面重构与余量计算实验

采用某商用三坐标测量仪，对某型号叶片进行三坐标测量，获得的数据如图6所示。

图6 三坐标测量仪测量的原始数据 图7 重构的叶片表面

采用本文第1节所述方法，在C++语言平台上进行重构实验，得到的叶片表面如图7所示。

采用理论截面数据与测量数据重构出的表面采用本文第2章所述的方法计算理论截面的余量，计算获得的余量结果与商用三坐标测量仪进行对比，如表1所示(Ⅲ，Ⅳ，Ⅴ截面)。

表1 余量计算结果对比

结果表明本文所采用的余量计算方法与商用的三坐标测量仪所给测量报告的结果相近，最大误差绝对值为0.003 205 mm，最小误差绝对值为0.000 168 mm，远远小于叶片公差带范围，验证了本文所提出的余量计算方法的有效性。

4.2 航发叶片材料去除率模型建模

材料去除率模型与多种因素有关，本文为简化实验因素，针对式(18)进行材料去除率模型的建立。实验装置采用带有精准力控的砂带磨抛装置，其稳态力控制精度可以达到±0.1 N，砂带线速度可在0～3000 r/min内实现动态调节。

实验前，本文对砂带特性进行评估，实验进行期间所选用砂带均处于稳定磨损期内，采用恒定3 N正压力进行磨抛实验，根据加工经验，在实际加工中，砂带线速度处于500～1500 r/min内可以达到一次磨抛成型的去除余量范围，因此我们选用500 r/min、800 r/min、1000 r/min、1200 r/min、1500 r/min五种砂带线速度进行材料去除率的建模。

为避免机器人运动学插补运算带来工件进给速度的差异，本文在实验中忽略每条刀路首尾部位的去除余量，将去除量平均值作为该速度下的去除量。同时由于叶盆与叶背的曲率分布具有较大差异，砂带轮与叶片的接触状态也有较大差异，因此本文分别对叶盆与叶背进行建模。建模结果如图8所示。

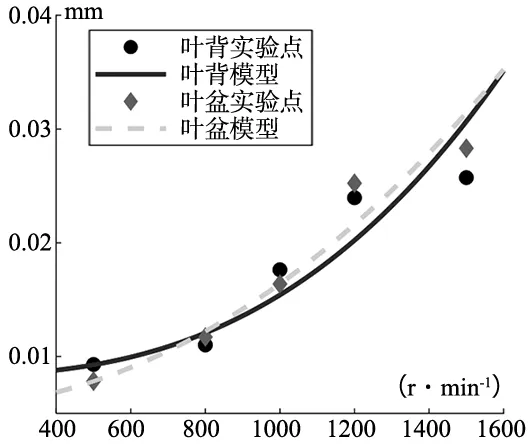
图8 叶片材料去除率建模结果

4.3 定量去除实验

本文4.1节与4.2节分别对余量计算与材料去除率建模进行了实验，为自适应定量去除加工提供了先验基础条件，本节将4.2节中拟合得到的材料去除率模型应用于实际加工中，仍采用恒定接触正压力3 N，通过调节砂带线速度进行磨抛实验，控制刀路点处的去除量。

磨抛实验前，本文先对一片未进行磨抛加工的叶片进行三坐标测量，通过计算叶片加工前的余量信息，结合已拟合得到的材料去除率模型，对砂带线速度进行规划。由于在靠近叶缘部位的刀路点处，叶片驻留时间较长，因此在拟合材料去除模型时，忽略该部位的点，为使刀路连续，本文将靠近叶缘部位的点的速度规划为理论值的0.5倍，如图9所示为规划得到的叶背与叶盆刀路上的砂带线速度分布。

(a) 叶背速度规划 (b) 叶盆速度规划图9 规划得到的刀路点上的砂带线速度

利用该刀路工艺进行磨抛加工，对加工后的叶片进行三坐标测量，某截面叶背与叶盆的轮廓度误差分布如图10所示。

(a) 叶背轮廓度误差 (b) 叶盆轮廓度误差图10 加工后某截面轮廓度误差

由图可知，利用本实验规划得到的砂带线速度数据进行磨抛加工后的轮廓度误差分布相对于理论线更加均匀，在余量较大的部位，去除量也较大，由此验证本文所提出理论的可行性与有效性。

5 总结

本文针对航空发动机叶片加工磨抛工序中的定量去除技术进行了研究，利用三坐标测量得到的数据计算加工余量。通过将砂带线速度作为加工时的控制因素，对航发叶片的材料去除率模型进行了建模。最后针对该方法进行了实验，结果表明本文所提出与采用的方法，能够可信地作为加工余量的计算方法，同时可以建模出了叶片两型面的材料去除率模型。针对未经过磨抛加工的叶片进行了磨抛加工，最终经测量，本文所提出的方法可以在加工余量分布不均匀的情况下，使最终的型面轮廓度误差更接近于理论规划量，从而验证了本文方法的可行性。但由于本文所开展实验次数的限制，未得到更加准确的材料去除模型，以及未对靠近叶缘部位的材料去除模型进行建模，因此本文实验效果未达到最佳。