改进NSGA2算法求解柔性作业车间调度问题*

杜晓亮，张 楠，孟凡云，王金鹤

(青岛理工大学信息与控制工程学院，青岛 266000)

0 引言

车间调度是车间生产制造的一个重要环节，能够充分利用现有的资源，合理的分配生产工序，减少加工时间和加工成本，优化生产目标，保证生产过程稳定运行。随着先进设备的出现，传统的作业车间调度已经不能满足社会发展的需求，柔性车间调度问题则被大多数学者研究。由于在实际的生产活动中需要考虑完工时间、总拖期时间、加工负载、最小成本等多个性能指标，因此单目标的柔性车间调度很难再反映实际的生产过程。

对于多目标优化问题，国内外学者提出了多种求解该问题的算法。如DEB等[1]提出的NSGA2算法，ZITZLE等[2]提出的SPEA算法，KNOWLES等[3]提出的PESA算法等。目前，NSGA2算法使用较为广泛。蒋浩等[4]在DEB提出的NSGA2算法的基础上，提出了一种基于快速排序的非支配集构造方法，并改进了其种群构造策略，设计了一类新的多目标遗传算法。

针对多目标柔性作业车间调度问题，张超勇等[5]使用NSGA2算法并改进其在非支配排序和精英选择策略上的不足，设计了改进的非支配排序遗传算法，并用层次分析选出最优妥协解。张守京等[6]针对NSGA2算法种群多样性低，运算速度慢等缺点，提出了基于拥挤度的自适应交叉算子。陈辅斌等[7]引入免疫平衡原理改进NSGA2算法的选择策略和精英保留策略。陈明等[8]考虑了粒子最大、最小收敛速度及相应边界条件，设计了一种应用于解决柔性生产调度的多目标粒子群算法。

另外,PENG等[9]提出了基于遗传算法的双资源柔性作业车间调度问题，在考虑机器柔性的同时加入了工人柔性，使问题更加实际化。ZHANG等[10]提出了基于遗传算法的可变邻域搜索方法求解该问题。吴树景等[11]提出了变邻域保优遗传算法，将遗传算法、变邻域搜索算法与精英保留策略相结合，得到了运算效率和求解性能均较好的混合算法。董海等[12]针对多目标柔性作业车间调度中的工人柔性、机器柔性和并行工序柔性，结合入侵肿瘤生长优化算法的算法结构和NSGA3中解的筛选机制，提出了一种多目标优化算法求解模型。

本文对传统的NSGA2算法提出改进，将工件的交货期定为硬约束，针对最小化完工时间、最小总负载、最小成本三个目标函数进行优化，避免了种群多样性降低造成的局部收敛同时加入邻域搜索提高了算法的局部搜索能力。

1 多目标柔性作业车间调度优化模型

1.1 问题描述

柔性作业车间调度问题可以描述为有n个待加工工件在m台机器上加工，工件集表示为J={J1,J2,…,Ji,…,Jn}，机器集为M={M1,M2,…Mk,…,Mm}。其中Ji表示第i个工件，Mk表示第k个加工机器。Ji工件有Oj道加工工序可以在不同的加工机器上进行加工，每个工件内的工序加工顺序已定。Oij表示第i个工件的j道工序。选择不同的加工机器会有不同的加工时间和能耗，因此调度的目标就是将工序合理安排到各机器，使得完工时间、加工成本等目标最小化。

同时，在加工过程中还应满足如下约束：一个工件内前一道工序加工结束后才能开始下一道工序；一道工序一旦开始不能终止；一道工序同一时间只能被一个机器加工；一个机器同一时间只能加工一道工序；工件间优先级是相同的；所有机器在0时刻都可用。

1.2 优化目标函数

在实际的生产车间中，能够及时完成车间任务、降低车间的生产成本并且使机器负载最小才能保证企业的经济效益。本文综合了完工时间、加工成本、机器总负载多个目标建立如下模型：

(1)

(2)

(3)

式(1)～式(3)中，目标函数f1～f3分别为最小化最大完工时间、最小化机器总负载、最小化加工成本；Cj为Jj的完工时间；pijk为Oij在机器k上的加工时间；xijk为决策变量；Oij在第k个加工机器上加工时，xijk=1，否则为0；CMk为第k个机器的单位时间加工费用。

2 基于改进NSGA2的多目标柔性作业车间调度算法

2.1 求解过程

基于改进NSGA2算法的多目标柔性作业车间调度算法流程图如图1所示。

图1 多目标柔性作业车间调度问题求解流程图

首先初始化种群，设置种群数量为200，然后进行非支配排序和拥挤度计算，把种群中的个体按照非支配排序的等级进行分级并计算出个体的拥挤度，之后进行选择交叉变异产生新种群，将父代种群和子代种群合并后再进行非支配排序和拥挤度计算，采用改进的精英保留策略生成新的种群，再进行邻域搜索，提高算法的局部搜索能力，最后非支配快速排序完成后进行下一次迭代，直到满足终止条件。

达到终止条件后，所得结果为一个包含多个解的Pareto最优解集。根据不同目标函数的权重进行归一化后选出最满意的解。对最满意解进行解码输出调度甘特图。

2.2 算法设计

2.2.1 解码和编码

本文采用的是基于实数的双层编码方式。编码结果如图2所示。第一层编码是对工序进行编码。基因为[0,1]之间的实数，经过排序后得到排序编码并对工序顺序编码重排后得到工序编码。如：有两个工件，第一个工件有两道工序，第二个工件有三道工序。

图2 基于实数的双层编码

工序顺序编码为S0=[1,1,2,2,2]。

第一层编码首先产生[0,1]之间的实数为：

0.540.120.680.330

那么排序后的排序编码为：S=[4,2,5,3,1]，用S对S0进行重排后得到工序编码为：S2=[2,1,2,2,1]。

第二层编码是为工序选用加工机器编码。基因向下取整后表示该工序采用其第几个可用加工机器。如：

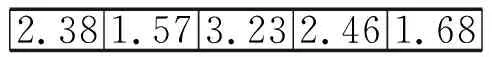
2.381.573.232.461.68

向下取整后为：

21321

第一位的2表示第一个零件第一个工序用它的第二个可用机器加工；第二位的1表示第一个零件的第二个工序用它的第一个可用机器加工，以此类推。

解码采用贪婪式解码算法。具体如下：首先按照工序在序列上的顺序进行解码，然后将每道工序安排到该工序的加工机器上的尽可能早的时刻进行加工，直到所有的工序都安排在最佳可行的地方为止。

2.2.2 Pareto排序

本文采用文献[1]提出的快速非支配排序算法，时间复杂度为O(MN2)。

2.2.3 选择交叉变异

本文采用二元联赛选择算法，优先选择快速非支配排序过程中等级低的个体，当等级相同时，选择拥挤度小的个体。交叉方式为两点交叉，变异方式为单点变异。

2.2.4 改进的精英保留

原始的NSGA2算法中，根据支配关系，将支配等级低的个体加入到新种群中，等级相同时将拥挤度小的个体放入种群中，直到种群规模达到N。这种精英保留策略是将所有的精英进行保留，可能会导致快速收敛或者收敛于局部最优解。因此，本文设计了改进的精英保留策略如图3所示。设置参数α，将前N×α个个体直接加入到新种群中，剩余的N×(1-α)个个体从次优平面上随机选择。

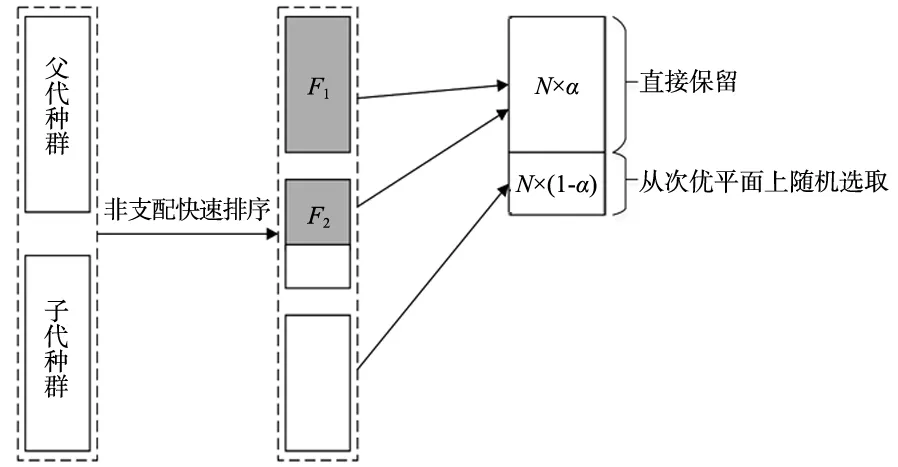
图3 改进的精英保留策略

2.2.5 邻域搜索

根据编码结构的特点，对种群中的个体进行邻域搜索。邻域搜索方式为单点变异，如图4所示，若选择变异基因位于工序部分，则对变异后所有工序编码部分基因按2.2.1节描述的方式重排后进行解码计算目标函数值；若变异基因位于机器编码部分，则从该工序可选机器中随机选取其他机器代替，而后计算目标函数值。将邻域搜索前后的值进行比较，将最优值进行保留。

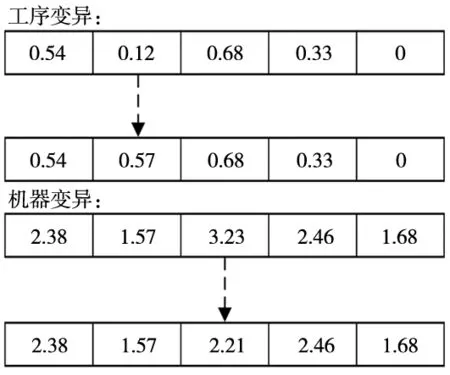
图4 基于单点变异的邻域搜索

3 仿真与结果分析

3.1 标准实例实验测试

为了验证本文算法的有效性，采用文献[13]不带释放时间的8×8标准实例进行测试。测试结果如表1所示，表中给出了GA、SPT[14]、张算法[5]的结果和本文算法的结果。由于Pareto解有多个，选取其中一个进行对比。从表中可以看出，本文算法在最大完工时间和机器最大负载两个性能指标上优于或等于其他算法；在总负载时间上仅次于张算法。由此可见，本文算法在求解多目标柔性作业车间调度上能得到比较好的结果。

表1 8×8实例测试结果的比较

3.2 实例仿真

为进一步体现算法的实用性，采用文献[6]中的数据如表2所示，并合理加入机器生产成本数据进行仿真。优化目标为最大完工时间、最大负载、最大加工成本。参数设置如下：种群规模设置为200，迭代次数为80，交叉概率为0.8，变异概率为0.1，邻域搜索次数为4，精英保留系数为0.9，目标函数的权重分别为0.6、0.2、0.2。通过MATLAB对以上实例进行仿真分析，得到各个调度目标进化过程曲线图、Pareto解集图、最优调度甘特图。

表2 6×6柔性作业车间调度问题实例数据

图5中随着迭代次数增加，各个目标函数值不断进行优化，算法具有良好的收敛性。在迭代次数达到50次之后，目标函数值趋于平稳。为了体现改进的NSGA2算法的有效性，绘制了如图6所示的帕累托前沿对比图。图中可以较明显的看出经改进的NSGA2算法可以得到更好的一组解。

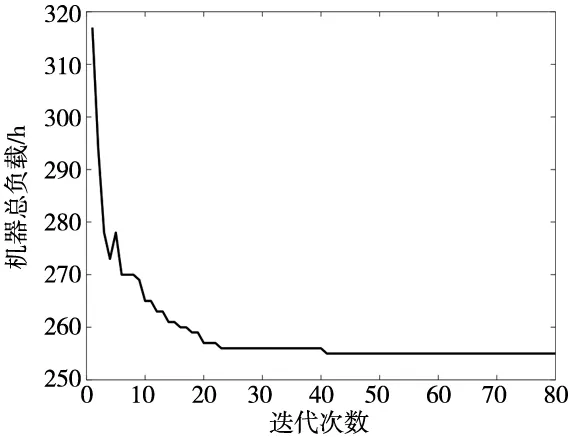
(c) 机器总负载的迭代曲线图5 种群进化迭代图

(a) 完工时间的迭代曲线 (b) 生产成本的迭代曲线

图6 帕累托前沿图 图7 改进后最优调度甘特图

本文算法在迭代完成后，会得到一组Pareto解集，去掉重复解后得到如表3所示的最优解集表。表中每个解均为最优解，且各个解之间互不支配。为了考虑问题的实际性，为每个目标函数设置不同权重，完工时间、机器总负载、生产成本分别为0.6，0.2，0.2。对各个目标函数进行归一化处理后，得到最优调度甘特图。图7为改进后算法得到的最优调度甘特图。图中6-1表示第6个工件的第1道工序；3-2表示第3个工件的第2道工序。算法改进前后各个目标函数值对比如表4所示，原始NSGA2算法中最大完工时间为69，机器总负载为260，生产成本为1 011.5。改进后算法最大完工时间为61，机器总负载为260，生产成本为995。经对比发现，完工时间优化了8个单位，优化了11.6%；机器总负载相同；生产成本优化了16.5个单位，优化了1.6%。

表3 Pareto最优解集

表4 算法改进前后各个目标函数值对比分析

4 结束语

针对多目标柔性作业车间调度问题，本文设计了改进的NSGA2算法。算法设计了一种基于实数的双层编码方式，避免了种群中的个体在交叉变异过程中产生不可行解。针对原始NSGA2算法在种群迭代过程中出现的提前收敛或局部收敛问题，设计了改进的精英保留算法，另外增加了邻域搜索提高了算法的局部搜索能力。通过仿真实验分析，验证了算法的有效性和可行性。此外还可以考虑将本文算法应用于实际车间生产过程中，以满足实际生产的需求。