分段线性刚度能量阱及在端铣加工中的分析*

李浩田，王海芳，李凌轩，陈晓哲

(东北大学秦皇岛分校控制工程学院，秦皇岛 066004)

0 引言

端铣加工中，刀具的振动会增大误差，严重时甚至会损坏机床。目前，减少刀具振动的主要方法是限制主轴转速，背吃刀量，进给速度等加工参数。托贝斯[1]研究了不同种类机床加工时的振动。ALTINTAS[2]研究了切削力和加工参数的关系。单文桃、邬舟平、雷涛等[3-5]研究了加工中机床主轴的稳定性。TLUSTY 、廖伯瑜等[6-7]研究了不同机床在加工中的模态。但是限制加工参数会带来一些问题，如：降低加工效率、加工成本提升等。故考虑用动力吸振器来进行端铣加工的制振。

动力吸振器可以被分为三类：被动型动力吸振器，半主动型动力吸振器，主动型动力吸振器。当动力吸振器的固有频率和主系统的激励频率相近时，动力吸振器的制振效果才能达到最优。张震坤、郎君、贾富淳等[8-10]做了此方面的研究。非线性刚度能量阱本质上是一种被动型动力吸振器。但是它的刚度可以随位移改变。因此其具有简单的结构和带宽制振能力。YAO等[11-12]将能量阱分为两类：接地能量阱和不接地能量阱。对于端铣制振，优先选用接地能量阱，因为能量阱的参数在很大程度上影响整体刚度矩阵的特征值，进而影响刀具端点的振动。背户一登等[13]发现了可以优化动力吸振器参数的定点原理。

端铣加工中会出现不同的主轴转速，机床的结构也比较特殊。这要求安装在机床上的动力吸振器要具备对刀具端点的带宽制振能力且结构简单。非线性刚度能量阱是最佳选择。随着非线性微分方程求解方法的发展，CHEUNG、LAU等[14-15]将增量谐波平衡法应用于越来越多的非线性系统。

上述研究使得用分段线性刚度能量阱降低端铣加工中刀具端点的振幅成为可能。相较于传统的限制加工参数的制振方式，其可以提高生产效率，简化加工流程。故提出了一种可以用于端铣工况的分段线性刚度的能量阱结构，建立了其振动表达式并求解，最后对其带宽制振能力进行了数值仿真。仿真结果表明其至多可以削减刀尖点40%的振幅。

1 能量阱结构

如图1所示，分段刚度能量阱被安装在端铣机床上，连接盘由套筒定位并由机床外壳上的螺纹固定。能量阱质量通过角接触球轴承和刀柄连接。轴承轴向间隙可以通过调整套筒轴向长度消除。为了增大零件刚度，机床外壳、套筒、连接盘和能量阱质量都合金钢制成。在连接盘和能量阱质量之间有9根围绕机床主轴均布的铅制等长杆。杆被分为3组，同组杆的直径相同。杆组2的直径是杆组1的直径的1.732倍，杆组3的直径是杆组2的直径的1.414倍。杆组2与连接盘之间的轴向间隙为Δ，杆组3和连接盘之间的轴向间隙为2Δ。

图1 分段线性刚度能量阱的结构

这样设置杆组的原因有两个，其一是3个杆组为1组可以防止能量阱质量产生转动；其二是根据文献[12]的研究，这样的3个杆组可以在连接盘和能量阱质量之间实现一个类二次方刚度的分段刚度。

角接触球轴承可以被视为一个刚度为kl，阻尼为cl的弹簧。能量阱质量为m，位移为ue。连接盘和能量阱之间的刚度为kn，阻尼为cn。杆组一中单个杆的刚度的1.5倍为kns，主轴-刀柄-刀具系统的质量矩阵，阻尼矩阵和刚度矩阵分别为M、C和K。刀具受到的切削力f。刚度kn和位移ue的关系如图2所示。主轴-刀柄-刀具-能量阱系统的简图如图3所示。

图2 刚度kn和位移ue的关系 图3 主轴-刀柄-刀具-能量阱系统的简图

2 振动表达式的建立

用最小势能原理结合有限元分析建立系统的振动表达式。简化系统并建立有限元模型如图4所示。x1～x12是节点坐标。1～6为单元编号，其中，1、2、3、4为机床主轴的轴段，5为刀柄，6为刀具。主轴上轴承的刚度和阻尼为k1和c1。机床拉杆的刚度和阻尼为k2和c2。此外，第i个单元的外径为Ri，内径为ri，密度为ρi，弹性模量为Ei。

图4 系统的有限元模型

系统上任意点坐标为x，时间为t。系统上任意点在主轴方向上的位移为u。根据拉格朗日插值：

u(x,t)=A(x)q(t)

(1)

式中，

应力σ和应变ε的关系为：

σ=Eε

(2)

ε和u(x,t)的关系为：

(3)

系统应变能为：

(4)

对应变能求变分：

δP(t)=LqT(t)δq(t)

(5)

式中，

惯性力对系统的虚功为：

δT1(t)=B1(t)δq(t)

(6)

式中，

轴承对系统的虚功为：

δT2(t)=B2(t)δq(t)

(7)

式中，

拉杆对系统的虚功为：

δT3(t)=B3(t)δq(t)

(8)

式中，

作用在能量阱上的非线性弹力为fn，则：

(9)

根据文献[12]的研究，如果Δ=0.01 mm，fn可以被近似视为ue的三次函数，且按分段线性的fn与近似的位移的三次函数的fn计算出的系统的响应基本是一致的。

(10)

弹力fn和位移ue的关系如图5所示。

图5 弹力fn和位移ue的关系

能量阱的力平衡方程为：

(11)

能量阱对系统所做虚功为：

δT4(t)=B4(t)δq(t)

(12)

式中，

切削力f的位置可近似视为在刀具端点。切削示意图如图6所示。h为实际切削深度，h0为刀具额定每齿进给，φ为切削角。h和h0的关系可近似为：

图6 切削示意图

h=h0cosφ

(13)

式中，

φ=ωst+φ0

ωs为机床主轴角速度；φ0为初始切削角。根据图6，只有(2k-0.5)π≤φ≤(2k+0.5)π(k是自然数)时，单个刀齿受到的切削力fi不为0：

fi=kFcosβ(a-u7)h

(14)

式中，kF为切削力系数；β为刀具螺旋角；a为切削宽度。刀具有两刃,所以f是f1和f2的和。u7相对h非常小，可以忽略，则：

f(t)=kFcosβah0cos(ωst+φ0))|

(15)

切削力对系统做的虚功为：

δT5(t)=B5(t)δq(t)

(16)

式中，

B5(t)=f(t)A(x7)

根据最小势能原理：

δP(t)-δT1(t)-δT2(t)-δT3(t)-δT4(t)-δT5(t)=0

(17)

将式(5)、式(6)、式(7)、式(8)、式(12)、式(16)带入式(17)，得：

(18)

式(18)可以被写为：

(19)

式中，

联立式(10)、式(11)、式(19)，有：

(20)

式中，

3 振动表达式的求解

根据傅里叶变换：

ui=ai0+ai1cosωt+ai2cos2ωt+ai3sinωt+ai4sin2ωt
ue=ae0+ae1cosωt+ae2cos2ωt+ae3sinωt+ae4sin2ωt
f(t)=b0+b1cosωt+b2cos2ωt+b3sinωt+b4sin2ωt

(21)

设：

S(t)=[1 cosωtcos2ωtsinωtsin2ωt]
Cs(t)=dia[S(t)S(t)S(t)
S(t)S(t)S(t)S(t)S(t)]

(22)

Ai=[ai0ai1ai2ai3ai4]
Ae=[ae0ae1ae2ae3ae4]
A=[A1A2A3A4A5A6A7Ae]T
B=[0(1×30)b0b1b2b3b40(1×5)]T

(23)

故：

(24)

另τ=ωt，则关于t的微分方程组(20)可以被写为关于τ的微分方程组：

(25)

根据增量谐波平衡法对式(25)设置增量：

(26)

忽视二阶小量，根据泰勒公式，式(26)可被写为：

N=R-ΔωH

(27)

式中，

根据式(24)：

(28)

根据式(22)、式(24)、式(28)和伽辽金法，式(26)可被化为：

NsΔA=Rs-ΔωHsA

(29)

式中，

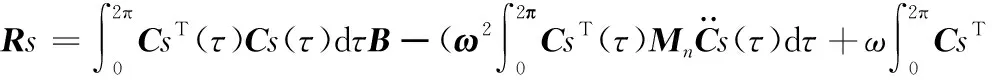
式(29)是ΔA和A的关系式。其可以被用于求解式(20)。给A一个初值，并根据式(29)计算ΔA的值。之后，令A=A+ΔA，用新的A计算新的ΔA，再令A=A+ΔA。重复此过程直到Rs的范趋近零。带入式(24)得到式(20)的解。

令：

(30)

为了求得A，每次迭代都需要求出Ns和Rs。如果每次都用常规方法计算I，计算会十分麻烦。计算流程可以按下述方式简化：

(31)

式中，

g1～g15的表达式如表1所示。

表1 g1～g15的表达式

I1～I15是常数矩阵，先算出值再带入式(31)，迭代过程会简化。机床主轴和刀柄的材料为40Cr，刀具材料为高速钢W14Cr4VMnRE，变量取值如表2所示。

表2 变量取值

4 数值仿真

根据文献[12]的研究，在计算系统的响应时，可以将能量阱质量受到的分段线性的弹力近似成位移的三次方函数的弹力。用MATLAB软件的脚本功能建立仿真模型，先将表2的变量取值带入式(20)，可以得到一个八元非线性微分方程组，根据此方程组可以得到Mn、Cn、Kn、Gn；再将这4个八阶矩阵代入式(29)，可以得到ΔA与A的迭代关系；在式(29)中，只有Hs是常值矩阵，为简化仿真时的迭代计算量，先由表1求I1-15，之后在每次迭代时，用式(31)求I再求Rs与Hs。迭代时，矩阵A中各变量初始值取0.01，即可求得刀具端点和能量阱的时域响应，由各频率下的时域响应可得其频域响应。

常规的端铣机床的主轴转速ns在1000 r/min和5000 r/min之间。刀具端点的频域响应a7如图7所示。主轴转速为1000 r/min、3000 r/min和5000 r/min时，无能量阱时刀具端点振幅分别为0.42 mm、0.33 mm和0.27 mm，有能量阱时刀具端点振幅分别为0.26 mm、0.24 mm和0.20 mm。能量阱质量的频域响应ae如图8所示。主轴转速为1000 r/min、3000 r/min和5000 r/min时，能量阱时质量的振幅分别为0.31 mm、0.27 mm和0.22 mm。根据图2，当能量阱的位移达到0.01 mm、0.02 mm时，二、三阶刚度生效，故能量阱在振动中，三阶刚度都发挥了作用。

图7 刀具端点的频域响应 图8 能量阱质量的频域响应

5 结论

提出了一种可以应用于端铣加工的分段线性刚度能量阱结构；其可以实现主轴转速介于1000 r/min～5000 r/min之间时对刀具端点的带宽制振；其可以在一定程度上解决传统限制加工参数的制振方法带来的限制；其制振能力总体上随着主轴转速增加而降低，至少可以降低刀具端点25%的振幅，至多可以降低刀具

端点40%的振幅；只有当能量阱的位移足够大时，带宽制振能力才能体现。