基于固有频率的丝杠预紧力衰退检测技术研究

谢经伦，顾祎程，冯虎田，周长光，张向东，顾 頔

(南京理工大学机械工程学院，南京 210094)

0 引言

滚珠丝杠副进给系统目前多被应用于机床行业，而滚珠丝杠作为滚珠丝杠副进给系统的核心部件，其性能质量直接决定了进给系统定位精度、承载能力的高低，目前行业提升丝杠性能的主要方式为对丝杠施加预紧力，因此预紧力可认为是滚珠丝杠副最重要的参数指标之一[1-3]。目前对滚珠丝杠预紧力进行检测的方法多需将丝杠从工作环境中脱离并搭架于试验台上，这不仅大大提高了检测成本，频繁的拆装也会降低进给系统整体刚度。因此实现一种对进给系统中滚珠丝杠副预紧力的快速简便检测方法是有必要的。

目前，针对滚珠丝杠预紧力方面的研究有很多。VERL等[4]研究了丝杠转速与丝杠预紧力间的关系，发现转速升高会使丝杠预紧力值增加。FENG等[5]研究了不同丝杠预紧力下的进给系统固有频率变化情况，发现随着预紧力的提高，进给系统固有频率会随之增加。ZHOU等[6]通过设计的预紧力可调滚珠丝杠，实现了对不同预紧力下滚珠丝杠副的振动信号的测量，并进一步的研究了振动信号与预紧力之间的关系。王志荣等[7]研究了丝杠不同预紧力对运行温升的影响，对丝杠实际使用的温度补偿具有重要意义。ZHANG等[8]建立了三种不同状态下的丝杠预紧力退化模型并通过跑和磨损试验进行了验证。ZHANG等[9]提出了一种新的预紧力计算公式并设计了新型的阻力矩测量系统，实现了对预紧力更高精度的测量，然而对丝杠阻力矩的测量需要将丝杠置于专用的测量试验台。聂从辉等[10]提出了一种将EMD与MSE结合的信号处理办法，能够从振动信号中实现对滚珠丝杠预紧力的判断，然而该方法难以在高背景噪声的试验条件下对丝杠预紧力进行测量。

综上所述，目前国内外针对滚珠丝杠副预紧力的检测方法虽然也有一定的研究，但多数都是通过离线检测动态转矩来间接获得滚珠丝杠副预紧力。本文从预紧力与固有频率之间的关系出发，通过建立动力学方程来得到固有频率与丝杠预紧力之间的关系，再利用动力学方程获得固有频率-预紧力特征集并用于训练决策树支持向量机，最后通过锤击法来获取实际进给系统的固有频率值并代入决策树支持向量机中，从而实现对滚珠丝杠预紧力值的在线测量。

1 动力学方程的构建

为了能够分析丝杠预紧力与进给系统固有频率的关系，本文基于集总参数法建立滚珠进给系统的动力学模型[11]。建立的滚珠丝杠进给系统动力学模型如图1所示，图中工作台与驱动电机分别被等效为集中质量单元与集中转动惯量单元；丝杠按工作台位置被划分为三个等效的集中质量单元与集中转动惯量单元，相邻部分由弹簧与阻尼连接；滚珠丝杠副中的螺母、滚珠分别被等效为质量单元、弹性元件；轴承、导轨分别被等效为弹簧、阻尼。

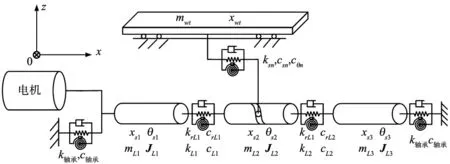
图1 滚珠丝杠副进给系统动力学模型

图1标注了进给系统的部分参数，完整的进给系统参数及定义如表1所示。

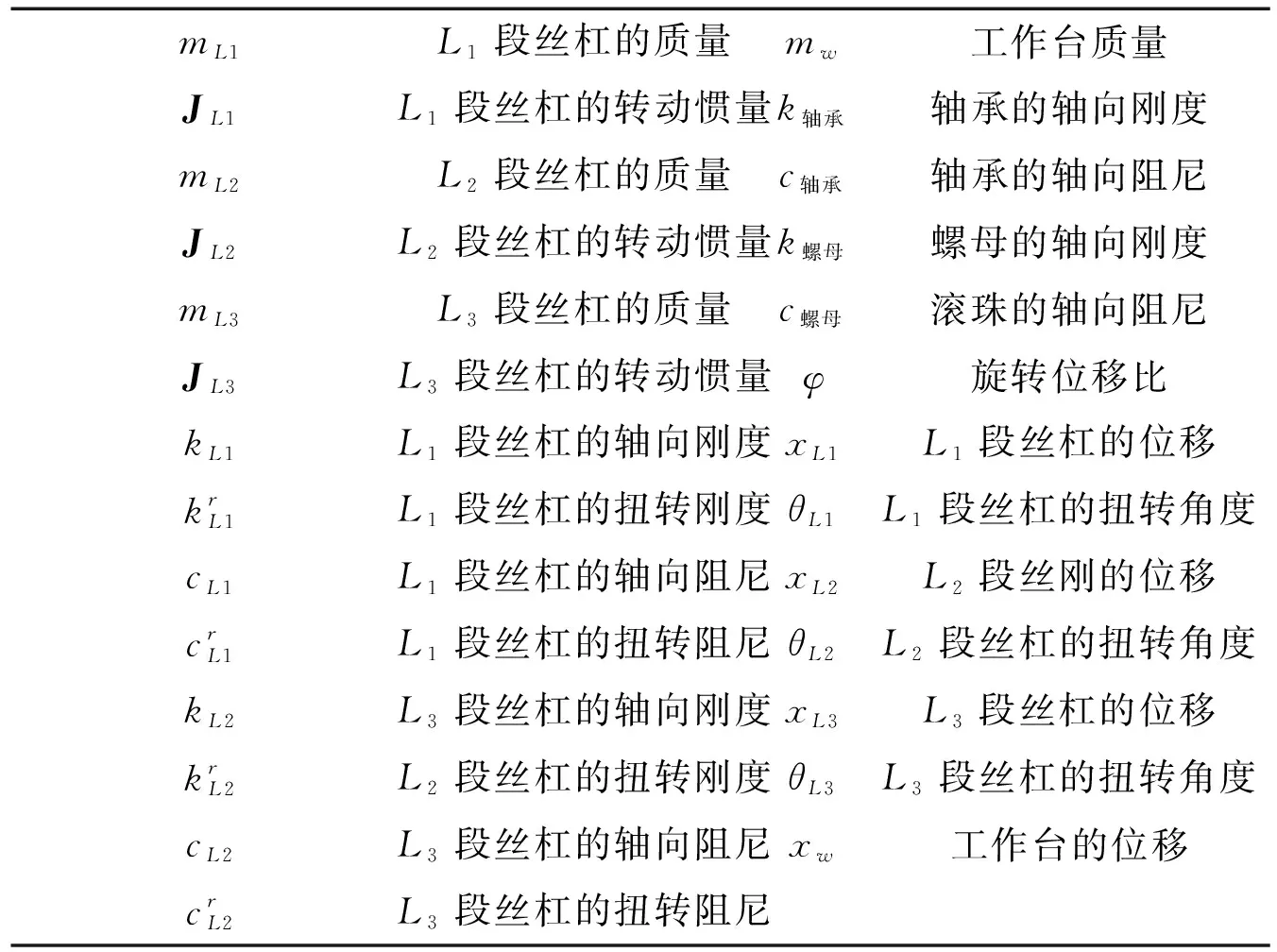
表1 符号说明

系统的总动能主要由丝杠动能、工作台动能组成，其中丝杠被分为了3段，其动能也按3段分别计算。当工作台工作到距左端位置为L1时，计算得到此时的系统动能为：

(1)

再由势能定理，可得到该进给系统的弹性势能与扭转势能分别为：

(2)

(3)

求得进给系统的动能、势能后，可通过拉格朗日第二类方程来求解进给系统的动力学方程。拉格朗日第二类方程的标准形式为：

(4)

式中，L为拉格朗日函数，L=V-P；qi为系统的广义坐标；Qi为在第i个广义坐标下的系统承受的广义力，在本文的试验条件下，电机未驱动，因此可认为Qi=0。联立式(1)～式(4)，可解得进给系统的动力学方程为：

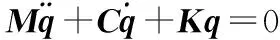
(5)

式中，M、C、K分别为进给系统的质量矩阵、阻尼矩阵以及刚度矩阵；q为进给系统的广义坐标向量，其中q=[xs1,xs2,xs3,xw,θs1,θs2,θs3]。对式(5)求解可得到系统的固有频率值，在实际的机床系统中，由于阻尼对进给系统固有频率的影响较小，因此求解时通常会令C=0，本文为简化计算同样令系统阻尼取0[11]，最终得到进给系统的详细动力学方程如下：

(6)

建立完成进给系统的动力学方程后，分析丝杠预紧力与系统固有频率的关系。由式(6)所示的动力学方程可知，丝杠预紧力主要通过影响刚度矩阵K中的螺母刚度k螺母来影响进给系统的固有频率值。螺母刚度与丝杠预紧力的关系由下式可知：

(7)

式中，K′为与丝杠螺母副有关的固定参数，在文献[12]中有详细介绍；Fp为丝杠预紧力；z为螺母副内的滚珠数量；α为滚珠与滚道接触角；β为丝杠螺旋升角。

2 基于固有频率与决策树SVM的丝杠预紧力识别方法

2.1 支持向量机算法

SVM，即支持向量机，是现阶段一种常见的机器学习方法[13]。SVM基于统计学理论，基本思路是通过非线性变换将空间高维化，从而得到一组新的高维复杂空间，在此空间中寻找最优的线性分类面，从而使空间正负类之间有最大的分类间隔。SVM问题可以分为线性可分和线性不可分[14]，对于线性可分问题，若假设现有训练样本(xi,yi),i=1,2,…,n,x∈Rm,y∈{+1,-1},n为样本数量,m为输入维数，则可定义最优分类超平面的公式为：

wx+b=0

(8)

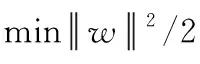
(9)

而当测试样本线性不可分时，线性可分问题转为线性不可分问题，此时可通过引入非负松弛变量与核函数进行解决。对于因噪点存在导致的线性不可分情况，通过引入非负松弛变量即可解决，基于式(9)可建立该情况下最优分类面的寻找公式：

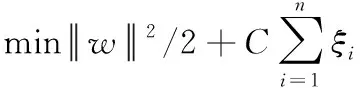
(10)

式中，ξi为松弛变量；C为惩罚函数，表示错误分类的严重程度，其值越大，对错误分类的惩罚越大。再基于Lagrange乘子法对式(9)、式(10)求解，便可得到最优的决策函数为：

(11)

式中，a为Lagrange系数。然而在大部分情况下，仅通过添加松弛变量仍无法解决样本的线性不可分问题，此时需要额外引入核函数，核函数的主要思想是将低维线性不可分的样本转至高维，从而在高维空间实现对样本数据的线性划分，核函数K(x,y)的主要作用是用于计算高维空间下的内积，根据Mercer条件，基于式(11)可建立线性不可分情况下的最优决策函数为：

(12)

2.2 基于决策树的支持向量机

传统SVM方法只能够利用分类面将样本数据分类成两类，即一组为正类别，另一组为负类别。当样本数据对分类数量有更高的要求时，传统的SVM方法便无法再适用了。借助于传统SVM方法的分类思想，本文提出了决策树SVM方法。决策树SVM可以看作是对传统SVM方法的叠加使用。令原始未分类的样本数据记父类样本，决策树SVM首先使用传统SVM方法对原始样本数据，即父类样本进行分类，得到两个类别，分为两类的样本数据记为子类样本。接下来再对子类样本进行二分类，得到4个次子类样本，以此类推，直至获得叶子节点，即无法再进行分类，最终形成决策树。以四分类问题为例，通过决策树SVM得到的树状图如图2所示。

图2 基于决策树的支持向量机多分类树状图

2.3 丝杠预紧力检测方法

本文提出了一种基于固有频率与决策树SVM来测量滚珠丝杠副预紧力的方法。首先通过式(6)和式(7)，以250 N为步进计算预紧力从1250 N～9000 N时的进给系统固有频率值变化情况，再将通过理论模型得到的预紧力值用于训练决策树SVM，训练完成后，通过试验采集丝杠不同预紧力下的进给系统固有频率值变化情况，将实际采集得到的固有频率值代入优化后的决策树SVM中，将输出的丝杠预紧力值与实际值对比，从而验证模型方法的准确性，具体流程如图3所示。

图3 丝杠预紧力检测流程

3 实例验证

为验证本文模型与检测方法的准确性，首先通过理论模型仿真不同丝杠预紧力下的固有频率值来训练决策树SVM，其次测量已知丝杠预紧力的滚珠丝杠进给系统固有频率值并代入决策树SVM中，通过将决策树SVM输出的丝杠预紧力值与实际丝杠预紧力值作对比，来实现对本文模型的验证。为提高准确性，本文使用前四阶固有频率来进行决策树SVM的训练，利用前四阶固有频率值分别对丝杠预紧力预测。

3.1 实验条件与流程

本文使用的滚珠丝杠副进给系统装置是基于工业和信息化部重点实验室自主研发的滚珠丝杠副综合性能测试试验台，如图4所示。在滚珠丝杠副综合性能测试试验台中，滚珠丝杠副会带动工作台运动，随着运动时间的不断增加，滚珠与螺母内滚道、丝杠滚道之间的磨损会不断加剧，导致滚珠丝杠副的预紧力和刚性不断下降，从而模拟实际工况下滚珠丝杠副预紧力的衰退，为确认发生衰退后的丝杠预紧力值，本文根据JBT13814-2020规范的丝杠预紧转矩公式，通过测量丝杠的动态预紧转矩来计算丝杠当前状态下的预紧力值。

图4 滚珠丝杠副综合性能测试试验台

滚珠丝杠副综合性能测试试验台选用的试验丝杠为山东博特产GD4010丝杠。试验时使用的测试设备有力锤(PCB/086C03，灵敏度2.358 mV/N)、数据采集系统(Prosig/P8012)、加速度传感器(M35B17/单轴加速度传感器，灵敏度501.33 mV/g)以及数显推拉力计(AFG200，量程±100 N，±0.25 FS)。通过力锤给予试验台一个冲击信号，再利用加速度传感器来对进给系统的响应进行采集，最后通过数据采集系统得到滚珠丝杠进给系统的频响曲线FRF并识别出当前状态的固有频率值。数显推拉力计用于获取丝杠的动态预紧转矩数据。测试设备的外观结构以及传感器的布置如图5所示，试验台的结构参数如表2所示。

图5 试验设备与流程

表2 进给实验台参数值

试验的具体操作过程如下：

(1)将加速度传感器沿丝杠轴向方向粘贴在待测丝杠法兰端面处；

(2)连接好加速度传感器、力锤、数据采集设备和计算机，在法兰端面选定锤击点，距离传感器尽可能远，并保证每次锤击位置和传感器位置不变；

(3)用力锤沿丝杠轴向方向敲击法兰端面锤击点处，给该进给系统输入一个激励信号，然后通过加速度传感器获取激励所对应的响应信号，并由计算机进行分析输出该进给系统的各阶特征频率大小；

(4)将锤击测出的主特征频率输入至优化后的SVM，记录此时滚珠丝杠副预紧力的数值大小，并与真实预紧力大小作比较。

3.2 预紧力特征集的采集与决策树SVM的训练

(1)构建预紧力特征集。根据上诉动力学方程计算不同预紧力下所对应的特征频率，构建预紧力特征集，用于后续的训练、预测，具体步骤如下：

步骤1：确定预紧力的变化范围为1250～9000 N；

步骤2：由二分类问题，取预紧力的间隔值为250 N，此时共有32组不同的预紧力值；

步骤3：将不同的预紧力值代入动力学方程中，计算并记录该预紧力下的进给系统前四阶固有频率值，记录结果如表3所示。

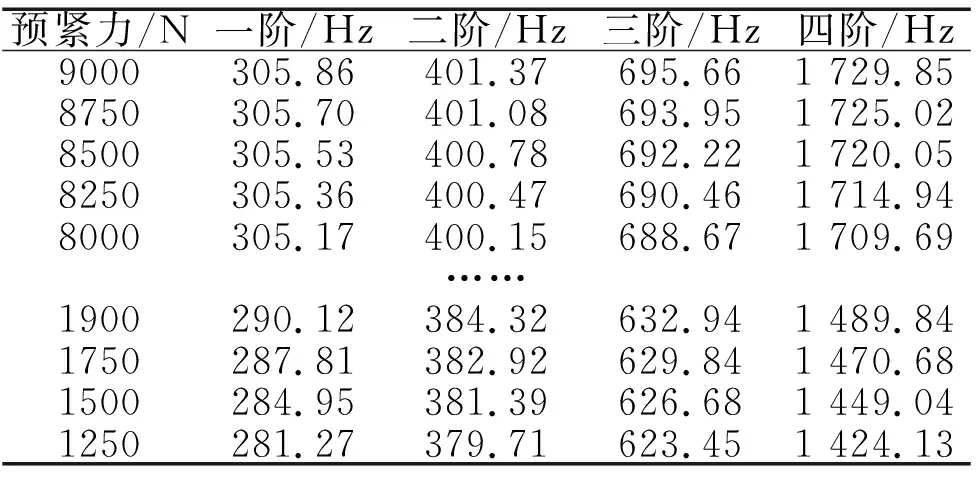
表3 预紧力变化范围内对应的各阶固有频率

(2)支持向量机训练预测。为提高预测的准确度，本文将计算得到的前四阶固有品频率作为输入，预紧力作为输出对决策树SVM进行训练。采用径向基核函数(RBF)对SVM的特征参数进行优化，当惩罚函数c和高斯核系数g分别为2和0.25时，测试集的预测效果最好。

3.3 实验验证

滚珠丝杠进给系统作为一个连续系统，其理论上其具有无穷多阶的固有频率值，然而考虑到在实际工况下难以采集到进给系统较高阶的固有频率值，因此本文仅取具有较大能量的前四阶固有频率，并分别利用这四阶固有频率对丝杠预紧力进行预测，取它们的均值作为最终的丝杠预紧力预测值。将工作台运行至行程的中间位置，锤击得到不同丝杠预紧力下的进给系统频响曲线如图6所示，其中固有频率在频谱图中以尖峰的形式存在。

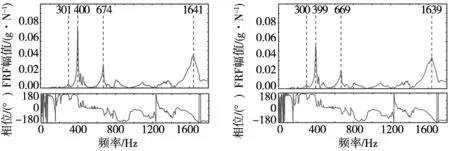
(a) 6497 N (b) 6021 N

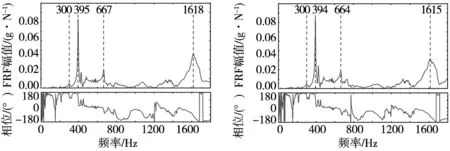
(c) 5494 N (d) 5167 N

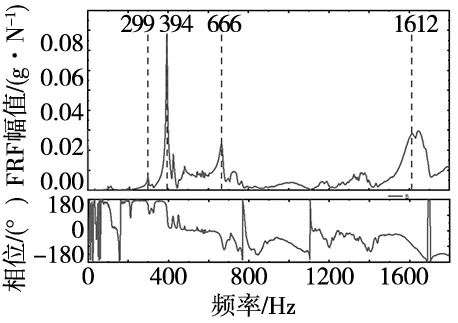
(e) 4984 N图6 不同预紧力下进给系统频谱曲线

将实测得到的固有频率值代入优化好的决策树SVM中，得到的丝杠预紧力预测值及均值如表4所示。对比可发现，通过固有频率与决策树SVM能够较好的对丝杠预紧力进行预测，最终预测得到的计算误差在10%以内，由此认为该方法可行。

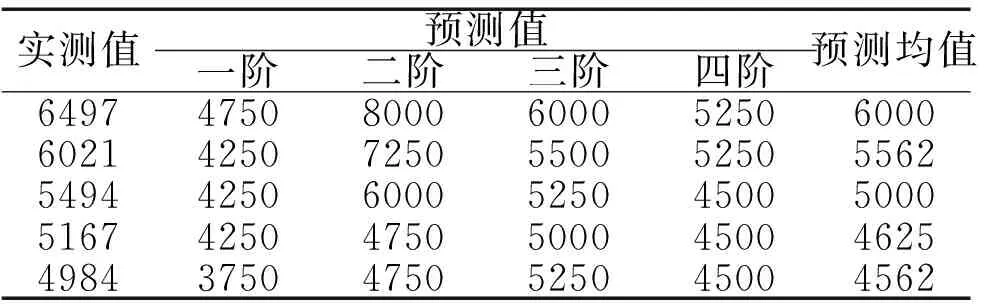
表4 丝杠预紧力实测值与预测值的对比 (N)

4 结论

本文从现有对滚珠丝杠预紧力检测方法的缺陷出发，提出了一种在线滚珠丝杠预紧力检测方法。首先通过建立的动力学模型寻找到了丝杠预紧力与进给系统固有频率的关系，再通过动力学模型获得不同丝杠预紧力下的进给系统固有频率值，并用于对决策树SVM进行训练，最后将实际测量得到的滚珠丝杠进给系统固有频率值代入决策树SVM中来对丝杠预紧力进行预测，将预测值与实际值进行对比，发现最终误差在10%之内，证明了本文提出的丝杠预紧力在线检测方法的可行性。