电磁轨道发射装置动态电感梯度分析
2022-06-08翟小飞李鑫航彭之然
翟小飞,李鑫航,刘 华,彭之然
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
电磁轨道发射装置是利用电磁力推动电枢在膛内高速运动的新型发射装置,由于没有传统火药武器的声滞制约,可以突破传统火药武器的出口速度限制,实现超高速[1-2]。电感梯度是电磁轨道炮的重要参数之一,其大小直接影响电枢电磁推力的大小,并对电磁轨道发射装置的发射效率和出口动能有着直接影响[3-5]。导轨中的电流分布以及导轨间的磁场分布是电感梯度直接决定因素,除了发射装置的结构、导轨截面形状、几何尺寸、导轨间距和材料属性等因素会影响电流密度分布,输入电流波形、导轨电流扩散过程以及速度趋肤效应等因素也会对导轨电流密度和空间磁场分布产生直接的影响,进而影响电感梯度大小[6]。
Kerrisk提出的高频电感梯度计算方法,以电流完全趋于表面为假设,而Grover提出的低频电感梯度计算方法,假设电流均匀分布于整个导轨,因此这两种方法计算出的电感梯度都不会随电枢发射过程而变化[7-9]。但是,电枢发射过程中导轨中的电流密度分布和空间磁场不断变化,导致装置储能电感和电感梯度是时变的,因此电枢发射过程中获得准确电感梯度变化值是获得推力变化过程的关键,也是提高系统仿真精度的关键。通过有限元软件进行电磁场仿真从而获得电感梯度等电磁参数,并将电感梯度等参数代入系统电气仿真模型与实际发射试验进行对比分析,是当前常用的一种做法。文献[10]进行了二维模型仿真分析,将获得的电感梯度用于电气系统仿真模型中,电枢出口速度的仿真值高于试验值。文献[11]根据三维模型中电枢推力曲线获得的电感梯度用于系统仿真,仿真结果与试验误差较大。
本文分别推导了导轨间磁场均匀分布和非均匀分布情况下电感梯度L′a数学计算模型。引入速度频率fv,能够在电枢静止的有限元仿真模型中,对电枢运动产生的趋肤效应进行仿真,从而获得动态电感梯度参数。建立了全系统仿真模型,将二维模型获得的单位长度电感Lu用于系统电感参数计算。将三维模型获得的电枢动态电感梯度L′a用于电枢推力计算。仿真结果与试验结果吻合较好,提高了系统仿真精度,表明提出的电感梯度分析方法和参数提取方法的正确性。
1 工作原理
电磁轨道发射装置工作原理是通电电枢在磁场中产生电磁推力从而推动电枢直线运动,电枢和导轨受力情况如图1所示。通电导轨在导轨内侧空间中形成了垂直纸面向里的磁感应强度B1,在导轨外侧空间形成了垂直纸面向外的磁感应强度B2。电枢在B1磁场区域产生向前电磁推力Fa,导轨中电流水平分量产生导轨外扩力Fo。由于速度趋肤效应和邻近效应,电流向导轨内侧汇集,电流密度在导轨长度方向呈三角形分布,这种三角形分布所产生的垂直分量会在导轨上产生前向推力。与此同时,电流从导轨“拐弯”流向电枢处,除了产生外扩力也会产生向前的分力,上述两部分前向分力之和构成了导轨总前向力Fr。
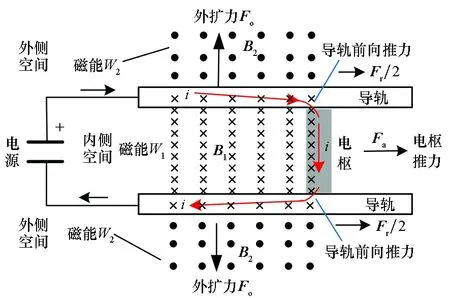
图1 电枢和导轨受力示意图Fig.1 Force diagram of the armature and the rail
电枢电磁推力大小的计算公式为:
Fa=L′ai2/2
(1)
根据式(1)给出的电枢推力与电流之间的关系,类似地设定导轨前向推力大小的计算公式为:
Fr=kri2/2
(2)
其中,L′a=dLa/dx定义为电感梯度,kr为导轨推力系数,i为导轨电流。通电导轨和电枢均受到了向前的电磁力,且两个电磁力均与电流平方i2成正比。
2 电感梯度理论分析
2.1 导轨间磁场均匀分布时电感梯度
电磁发射装置主要关心电枢推力大小,因此主要研究电枢推力对应的电感梯度的影响因素。
图2为两根矩形导轨构成的发射装置示意图。假设稳定电流I在导轨内均匀分布,电流密度为J,且导轨间的磁感应强度B均匀分布,导轨位于空气中。由于导轨沿y轴左右对称,导轨间中线处的磁感应强度B在z轴方向相互抵消,因此只有y轴分量By。根据毕奥-萨法定律,可以求解出坐标原点O处的磁感应强度为:
By=fB(J,h,w,s)
(3)
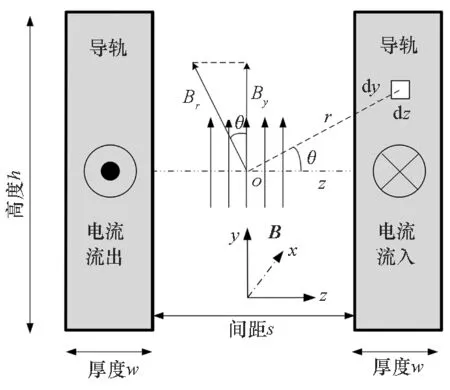
图2 矩形导轨结构形式Fig.2 Rectangle rail structure state
电枢电流为I,其推力大小的计算公式为:
Fa=ByI·s=L′aI2/2
(4)
推导出电感梯度表达式为:
(5)
由式(5)可以看出,电感梯度除了受到磁导率μ0影响外,只与导轨尺寸w、h以及导轨间距s相关。
式(5)表示了电流均匀分布条件下的电感梯度计算公式,这是一种电流扩散充分的“低频”电感梯度。导轨间磁感应强度实际情况是,z轴方向呈中间小、两边大的分布规律,在y轴方向上呈中间大、两边小的分布规律,低频时这种空间分布差异并不大可近似认为均匀分布,因此可以近似采用式(3)~(5)表示。
电枢发射过程中,由于电流扩散、邻近效应以及速度趋肤效应,电流在矩形导轨截面近似呈回形分布,且电流更集中在导轨内表面,这种电流分布效果与高频时电流分布效果类似。
根据上述特点,构建了电流回型分布模型,如图3(a)所示,左右电流分布是相同的,而导轨内侧比外侧的电流密度集中区域厚度更大。根据电流密度回型分布特点,将导轨拆分为4组等效导轨[12],每组导轨中的电流认为是均匀分布且相等的,其厚度由频率引起趋肤深度决定,如图3(b)所示。
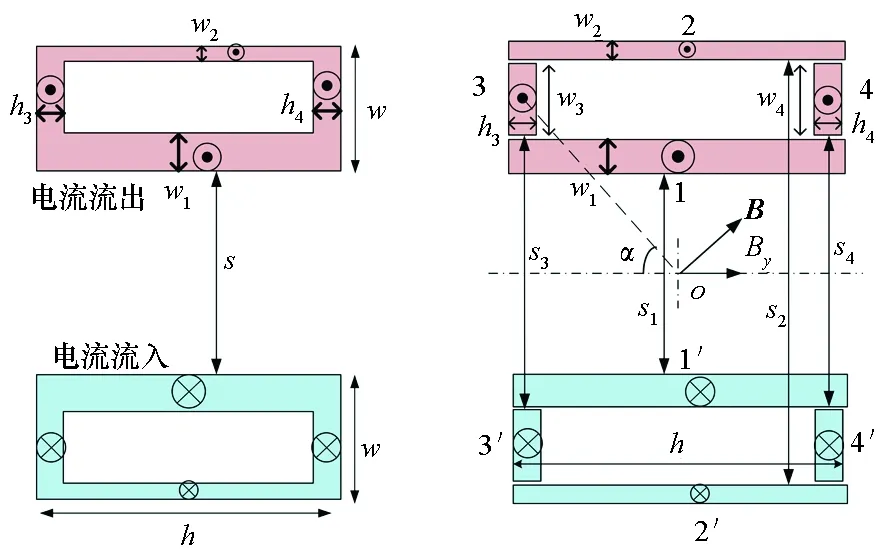
图3 高频电流回型分布导轨模型Fig.3 Model of the high-frequency current rounding distribution
将4组导轨的几何尺寸w、h和间距s以及各组导轨电流密度Jk代入式(3),可以分别得到4组导轨在中心O点处产生的磁感应强度大小为Byk。根据图3(b)所示的几何关系,第1和第2组导轨可直接使用式(3),而第3和第4组导轨则用α对式(3)进行修正:
(6)
其中,tanα=(s+w)/h。根据4组导轨电流密度相等的假设,且考虑到趋肤深度远小于w、h和s,原点O处的合成磁感应强度近似为:
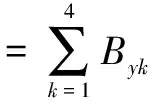
(7)
式中,Ax、Jx分别为4组导轨总面积和对应的电流密度,Kα为式(7)的中括号内容。按照轨道间磁场均匀分布的假设,根据式(4)可得高频电枢推力大小为Fahf对应的电感梯度为:
(8)
2.2 导轨间磁场非均匀分布时电感梯度
式(3)是导轨间磁感应强度B均匀分布条件下得到的近似公式,但电枢运动过程中导轨间磁感应强度随空间x-y-z位置和时间t不断变化。为了获得更加精确的磁感应强度分布情况,需要引入磁扩散方程。
忽略位移电流,根据麦克斯韦方程组得:
(9)
在空气环境的线性系统中,可以得到导轨间磁扩散方程:
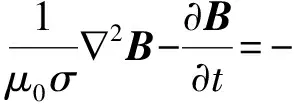
(10)
参考图2所示的坐标轴,忽略x、z两个方向分量,即磁感应强度只有y轴分量B=Byj,在x-z二维坐标系统中,导轨速度为零,电枢速度沿x轴方向大小为v,代入式(10)中得到磁感应强度的扩散方程式:
(11)
其中,σr为导轨电导率,σa为电枢电导率,Bry为导轨空间磁感应强度y轴分量,Bay为电枢磁感应强度y轴分量。根据式(11)以及相应的边界条件,可以计算出Bry和Bay。电枢推力沿x轴方向,其体积力密度计算式[13]为:
(12)
对电枢的体积力密度fa进行体积分可以得电枢推力和对应的电感梯度。
(13)
电枢发射过程中,电流密度J和磁感应强度B均随时间和空间不断变化,因此要获得精准的磁感应强度分布和电磁推力数值,需要引入有限元模型进行数值仿真[14-15]。
3 电感梯度仿真分析
3.1 二维模型有限元仿真
3.1.1 速度引起的趋肤效应分析
设定轨道厚度w=10 mm,轨道高度h=30 mm,轨道间距s=20 mm,导轨二维有限元仿真模型如图4所示。
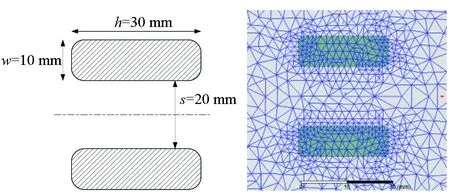
(a) 导轨尺寸(a) Dimension of the rails (b) 网格剖分图(b) Meshing graph图4 二维轨道模型Fig.4 Model of 2D rails model
根据文献[16]可知,电流频率和电枢速度所产生的趋肤效应可以在模型中采用扫频的方式进行涡流场分析,从而获得单位长度电感值。在ANSYS电磁场仿真软件系统中进行涡流场分析,首先需要确定电流频率范围。电枢在导轨高速运动过程中,不断将导轨新部分接入导电回路中,因此新接入的导轨就需要采用阶跃电流在导轨中扩散的模式进行分析,将阶跃扩散过程用稳态正弦电流所引起的频率趋肤效应来等效。式(14)给出了正弦电流趋肤深度δsin以及阶跃电流在导体中的扩散深度δstep的表达式[16-17]。
(14)
令δstep=δsin,可以得到电枢运动过程中速度趋肤效应所对应的频率fv(称为速度频率)的计算公式。
(15)
式中,v为电枢速度,λ为电枢与导轨接触的长度,fe为交流电流频率。当v=2 000 m/s、λ=20 mm时,对应的速度频率fv=10.13 kHz。
3.1.2 单位长度电感值
由于ANSYS电磁场仿真软件的二维涡流场采用模型空间磁场储能W来计算模型单位长度的电感值Lu=2W/I2,简称电感系数。根据输入电流频率(电流基波频率约为200 Hz)和速度频率(2 000 m/s对应速度频率为10 kHz),二维涡流场扫描频率范围定为100 Hz~10 kHz。导轨电流密度分布随频率fv变化的二维电磁场仿真结果如图5所示。
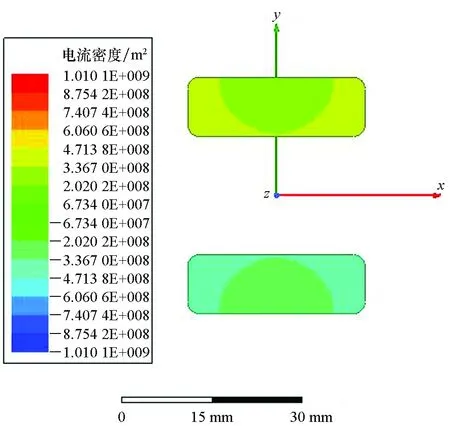
(a) fv=100 Hz
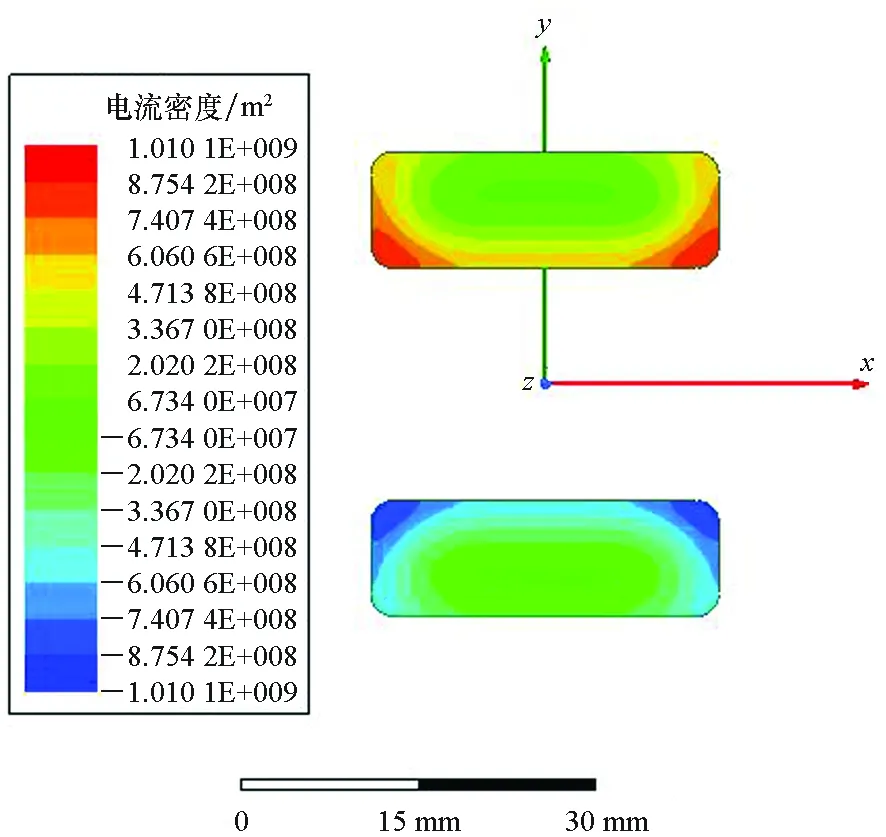
(b) fv=500 Hz
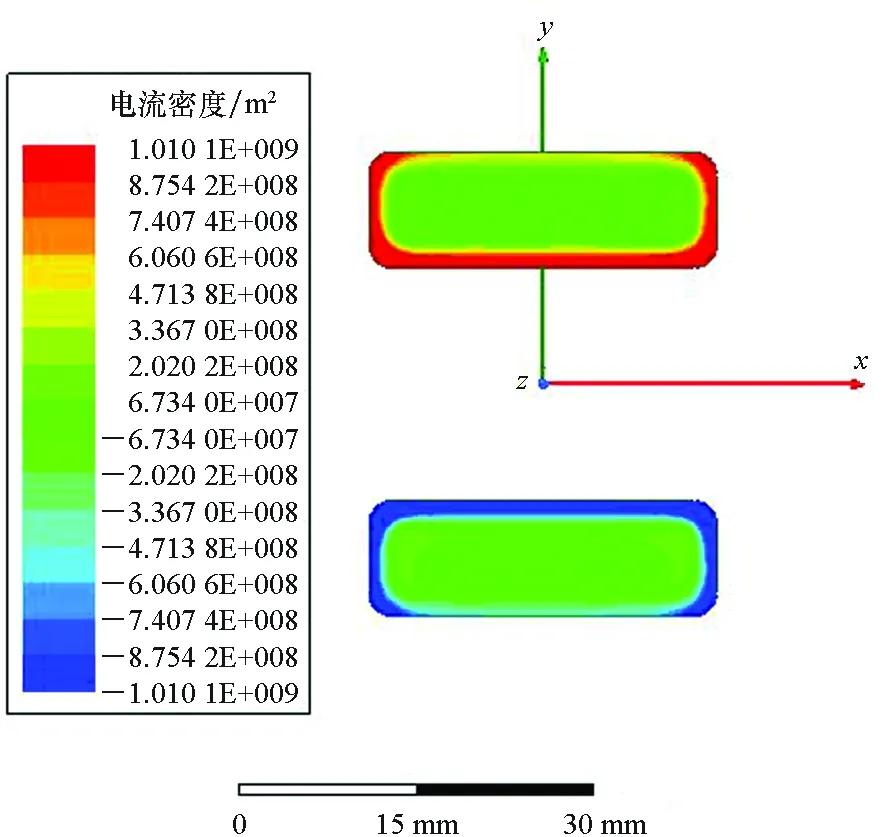
(c) fv=4 kHz
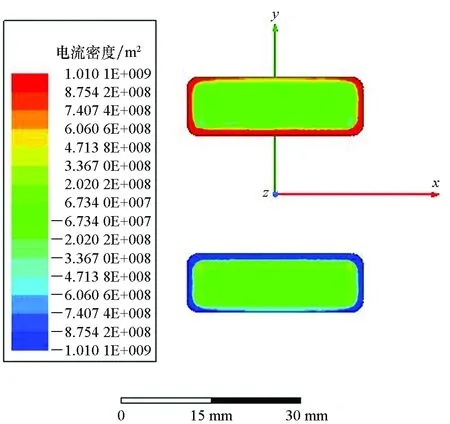
(d) fv=10 kHz图5 导轨的电流密度分布云图Fig.5 Cloud chart of the rail current
从图5可以看出,由于趋肤效应和邻近效应电流主要分布在导轨四个边且更集中在导轨内侧,频率越高电流越趋于导轨表面,也更集中在导轨内表面[18-19]。电流密度在导轨中的空间分布直接影响了导轨间的磁感应强度B的大小和分布情况,从而影响了空间磁场储能以及对应的电感系数Lu。图6给出了不同频率导轨中轴线上的磁场变化曲线图,图7给出了电感系数随频率变化曲线。
(a) 导轨中轴线(a) Middle line between rails
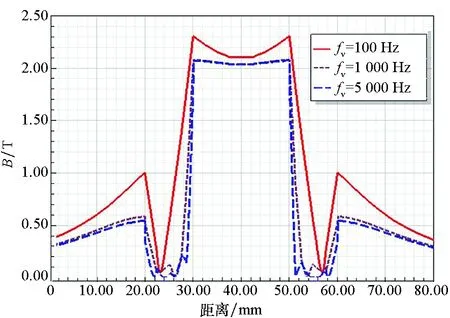
(b) 磁感应强度曲线(b) Curve of magnetic flux density图6 导轨中轴线磁感应强度随位置变化曲线Fig.6 The curve of B in rail middle line
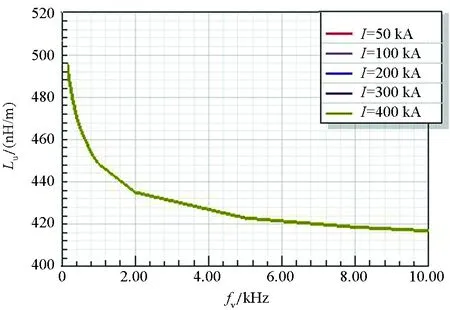
图7 电感系数随频率变化曲线Fig.7 Inductance coefficient varied with frequency
从图6可以看出,导轨间磁感应强度远高于导轨外空间,且无论是在导轨之间的内侧空间还是外侧空间,100 Hz条件下的磁感应强度大于1 kHz和5 kHz工况,同时1 kHz工况与5 kHz磁感应强度分布情况非常接近。可见fv较小时,导轨中电流扩散充分,导轨间磁感应强度越高,相应的电感梯度越高,即低频电感梯度(扩散充分程度)要大于高频电感梯度(趋肤明显),这种规律和Kerrisk高频电感梯度以及Grover低频电感梯度的规律是一致的。从图7可以看出,电感系数随着频率(即电枢速度)增加而逐步减小并趋于稳定,从式(14)、式(15)可以看出,v越高,fv越大,δsin越小,表明发射过程中,电流越来越集中在导轨内表面且趋肤深度逐步稳定,所以电感系数Lu逐步趋于稳定。分析可知,二维模型获得的电感系数反映了装置储能大小,因此根据电感系数和电枢位移可以计算出系统动态电感数值。
3.2 三维模型有限元仿真
采用ANSYS电磁场仿真软件对三维模型进行涡流场(eddy field)仿真,并根据电枢和导轨的电磁推力反推出对应的电感梯度。装置三维模型结构如图8所示。
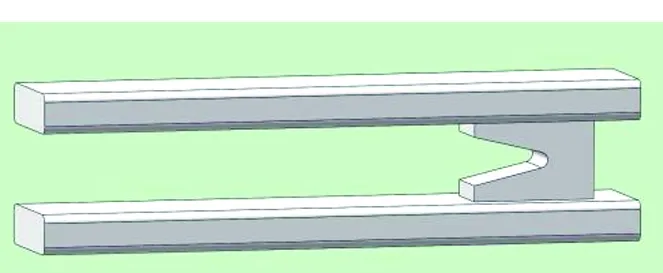
图8 装置三维模型结构Fig.8 3D structure of the launcher
涡流场扫描频率同样采用二维场的频率范围100 Hz~10 kHz。导轨和电枢上的电流密度J随频率的分布情况如图9所示。
推力随频率变化曲线如图10所示。从图10可以看出,电枢推力Fa和两根导轨前向推力Fr均随着输入电流频率增加而不断减小并趋于稳定。根据电枢推力Fr和输入电流i可以反推出电感梯度L′a。
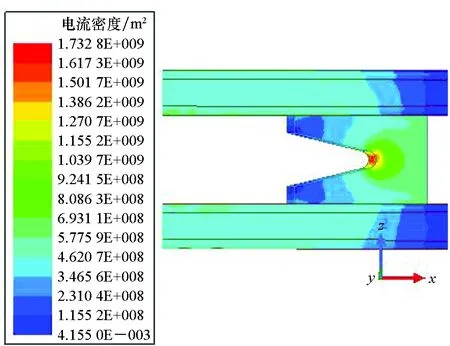
(a) fv=100 Hz

(b) fv=500 Hz
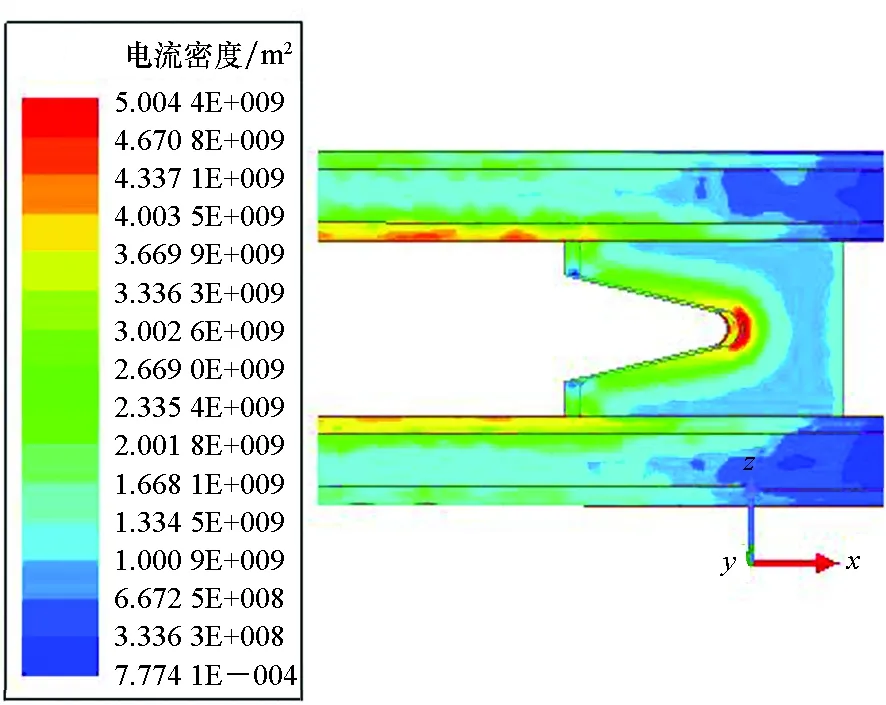
(c) fv=4 kHz
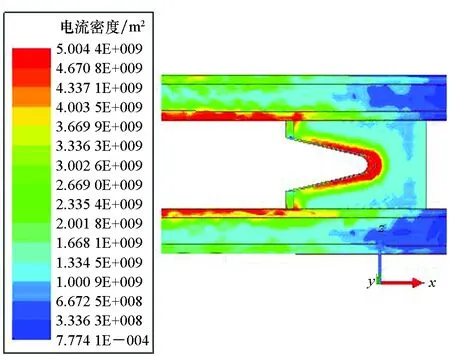
(d) fv=10 kHz图9 三维涡流场电流密度云图Fig.9 Cloud chart of the eddy 3D simulation
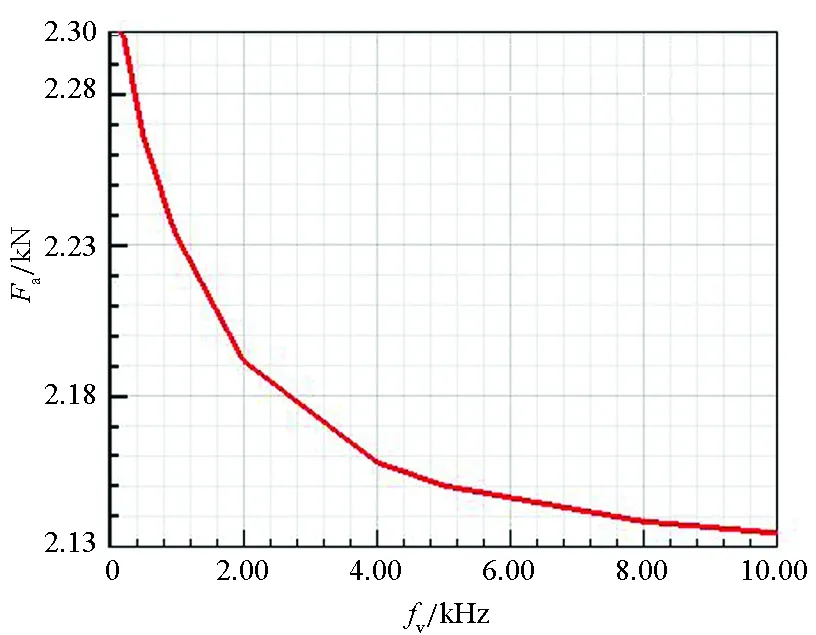
(a) 电枢推力曲线(a) Curve of armature thrust
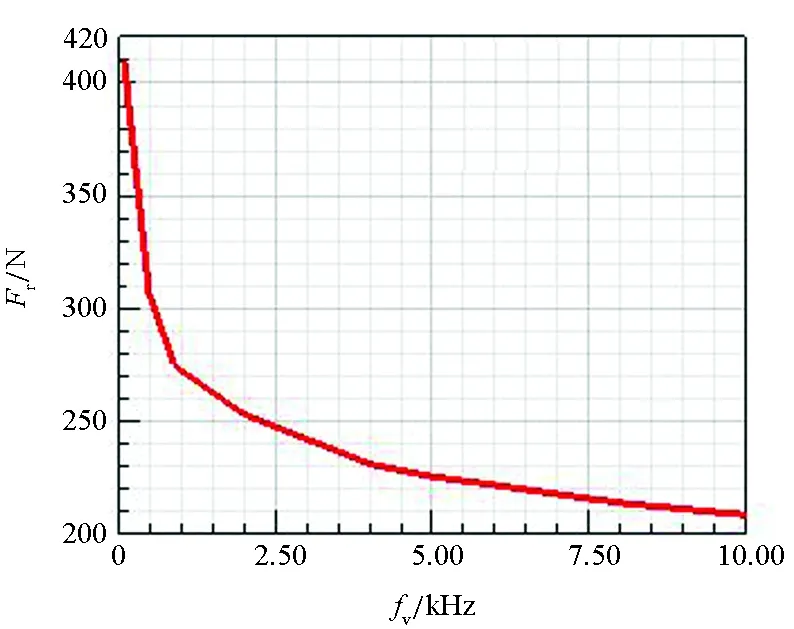
(b) 导轨前向推力曲线(b) Curve of forward thrust of rail图10 推力随频率变化曲线Fig.10 Curve of the thrust versus frequency
4 系统仿真和试验
发射过程中,由于电枢运动将导轨不断接入电气回路中,发射装置可以等效为电阻、电感随电枢位移不断增加的动态阻感性负载。Ra为电枢加枢轨接触电阻,其数值曲线是采用装置口部电压与电流实测波形计算拟合得到。发射过程中动态电感梯度L′a采用了三维模型仿真获得随速度频率fv变化的电感梯度,而系统储能所对应的电感Lm=L0+Lux,其中L0为电枢起点位置对应的初始电感,Lu为随速度频率变化的装置电感系数。根据装置动态阻感电气模型,构建如图11所示全系统电气仿真框图。
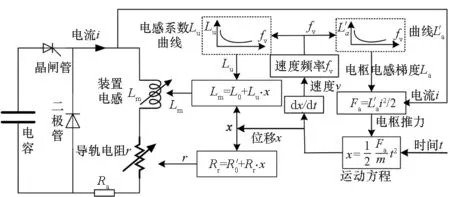
图11 电磁发射装置电气仿真系统框图Fig.11 Diagram of the electrical system simulation
从图11中可以看出,根据仿真得到的Lu曲线和L′a曲线,以速度频率fv为输入可以得到发射过程中实时的电感系数Lu以及电感梯度L′a,代入装置电感和电枢推力计算模型中,分别进行电气和运动模型仿真计算。根据电枢推力和运动方程得到电枢位移x,微分后得到电枢速度v,并代入式(15)得到速度频率fv,如此循环可以得到电枢运动过程中各物理量的变化曲线。利用Simplorer软件构建了电磁发射装置电气仿真模型并与发射试验结果进行对比。图12所示为电磁发射试验装置,图13为仿真和试验对比波形。

图12 电磁发射试验装置Fig.12 Electromagnetic launcher

(a) 电流曲线(a) Electric current curve
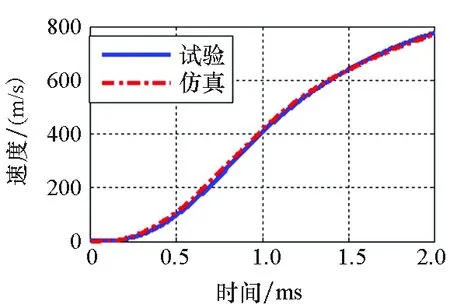
(b) 速度曲线(b) Velocity curve图13 发射试验与仿真对比Fig.13 Comparison of test and simulation
本次试验电枢质量为23 g左右,电枢出口速度为773 m/s,仿真出口速度为763 m/s。从试验和仿真对比可以看出,仿真和试验的电流峰值误差为0.8%,出口速度误差为1.29%。
5 结论
由于电枢发射过程中导轨电流密度和磁感应强度是动态变化的,引入速度频率fv参数,在有限元电磁仿真模型通过时谐分析提取了发射过程中动态变化的电感系数Lu和动态变化的电感梯度L′a。将Lu和L′a分别应用于电气仿真模型的电感和推力计算,极大提高了全系统的仿真精度。
