基于解析模式分解和随机减量技术的桥梁模态参数识别

2022-06-08杨勇宁平华王晟华旭刚温青

铁道科学与工程学报 2022年5期

杨勇，宁平华，王晟，华旭刚，温青,3

(1.广州市市政工程设计研究总院有限公司，广东广州510095；2.湖南大学风工程与桥梁工程湖南省重点实验，湖南长沙410082；3.湖南科技大学土木工程学院，湖南湘潭411201)

环境振动动力试验是工程结构模态参数识别应用最为广泛的方法[1-7]。该方法不影响工程结构的正常运营，测试结构在风、车辆和人群等随机荷载下的振动响应，采用随机子空间法、增强频域分解法等一些时域和频域方法识别结构模态振型、频率和阻尼比。随机减量技术(RDT)是一种常用的环境振动信号处理方法，通过该方法处理，可以获得类似于自由振动的随机减量信号。从随机减量信号中可有效提取结构的频率和阻尼比。该方法能较好的处理单模态环境振动信号，但处理多模态环境振动信号时，难以获得理想的结果[8]。为了克服随机减量技术在多模态振动信号处理中的缺陷，可提前对振动信号进行分解。经验模态分解(EMD)[9]是一种常用的、有效的信号分解方法，可将结构环境振动信号分解成一系列准稳态的本征函数(IMFs)。YANG等[8]利用EMD在信号分解方面的优势，提出了基于经验模态分解和随机减量技术(EMD-RDT)的结构模态参数识别，并用该方法识别一座高耸建筑的频率和阻尼比。华旭刚等[7,10]采用基于经验模态分解和随机减量技术的参数识别方法识别了南京长江桥梁的模态参数。经验模态分解筛选出来的本征函数有时并非单频率成分，存在模态混淆现象。为了避免模态混淆，WU等[11]通过改进EMD，提出了集成经验模式分解(EEMD)。然而，EMD和EEMD难以处理密频系统的振动信号分解，如大跨异型桥梁[6]。针对频率分布密集的振动信号，CHEN等[12]提出了解析模式分解(analytical mode decomposition，AMD)。该方法能将频率分布密集的振动信号分解成一系列单模态的子信号。WANG等[13-16]对该方法开展了系统研究。大跨异型桥梁具有频率分布密集、模态振型多方向耦合等特征，实测环境振动响应的频率分布会更加密集，直接利用随机减量技术难以有效识别多阶模态参数，基于EMD-RDT方法的识别效果也不理想。鉴于此，本文分析基于解析模式分解和随机减量技术(AMD-RDT)的桥梁模态参数识别方法。该方法首先利用AMD在信号分解方面的优势，将环境振动响应信号分解成一系列单模态子信号；然后，利用随机减量技术在随机振动信号处理方面的优势，从分离的子信号中提取随机减量信号；最后，采用最小二乘法按照单自由度系统自由振动函数从随机减量信号中识别结构的固有模态频率和阻尼比。本文首先详细阐述了AMD-RDT模态参数识别方法。然后通过三自由度振动系统仿真分析验证该方法的可行性，分析各参数对识别结果的影响，确定最优参数选择。最后，采用该方法识别了一座大跨度曲梁人行拱桥的固有频率和阻尼比。

1 模态参数识别方法

1.1 解析模式分解

解析模式分解是基于希尔伯特变换的一种信号分解方法[12]。该方法假设信号x(t)由n个具有相互独立频率区间的子信号x(d)i(t)(i=1,2,…,n)组成，如式(1)所示。

每个子信号具有显著的频率成分(ω1,ω2,ω3,…,ωn)。每个子信号在独立频率区间(ωb(n−i−1)<|ωi|<ωb(n-i))的傅里叶变换值与原信号的傅里叶变换在此区间的傅里叶变换值相等。基于解析模式分解的信号分解计算如式(2)和式(3)所示。

式中：s0(t)=0，H[.]表示希尔伯特变换，ωbj∈(ωi,ωi+1)(j=1,2,…,n-1)是n−1个二分点频率。

文献[12-16]对解析模式分解进行了详细论证和分析。通过解析模式分解，一个实测环境振动信号可以被分解为一系列单模态子信号，用于随机减量技术处理。该方法对频率密集的信号也能很准确的进行信号分解。

1.2 随机减量技术

式中：y(0)为初始位移；D(t)为单位初始位移、零初始速度的自由振动响应；ẏ(0)为初始速度；V(t)

为零初始位移、单位初始速度的自由振动响应；h(t)为单自由度系统单位脉冲响应函数；f(t)为外部激励。

对结构振动响应y(t)进行常数y0截取，获得交点时刻tr(r=1,2,3,…)。以时刻t r为起点的响应y(t-t r)可以视为由tr时刻的位移y(tr)和速度ẏ(t r)分别引起的自由振动响应、以tr时刻为起点的外部激励f(t-t r)引起的强迫振动响应的线性叠加，可表示为：

所有子样本函数y(t-tr)构成子响应过程Y(t-tr)，所有子激励函数f(t-tr)构成激励子过程F(t-tr)。假设f(t)是零均值平稳高斯过程，则y(t)是零均值平稳高斯过程，ẏ(t)也是一个零均值平稳高斯过程。因此，E[ẏ(t)]=0，E[f(t)]=0，将时间起点tr移至坐标原点(tr=0)，由此可得

由式(7)可知，子响应过程Y(t)是一个初始位移为E[y(0)]、初始速度为0的自由振动过程。由于实际测试中采样长度的限制，可将式(7)表示为

式中：N为子样本数，τ=t-ti。

1.3 参数识别

基于解析模式分解和随机减量技术的结构模态参数识别流程如图1所示。首先，根据实测环境振动响应功率谱，确定结构频率成分，使用解析模式分解(AMD)获得n个单模态的子信号y(d)i(t)。然后，对分解出来的n个子信号y(d)i(t)分别进行随机减量技术(RDT)处理，获得n个单模态的随机减量信号E(Y(d)i)。最后，从随机减量信号中识别结构频率和阻尼比。获得的随机减量信号具有单自由度系统自由振动的特征。单自由度系统自由振动函数可以表示为：

图1 基于AMD-RDT模态参数识别方法流程图Fig.1 Flowchart of AMD-based RDT modal parameters identification

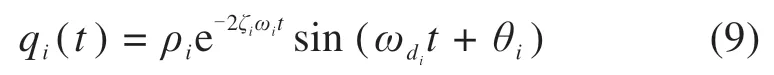
式中：ρi，ζi，ωi，ωdi和θi分别是第i个自由振动的振幅、阻尼比、固有频率、阻尼频率和相位角。其中阻尼频率由固有频率和阻尼比计算得到，故式中共有4个未知数。采用最小二乘法按公式(10)所示最优目标函数，可以得到4个未知数的最优解，由此实现结构模态频率和阻尼比的识别。

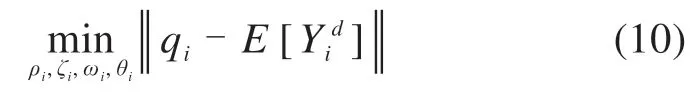
2 参数分析

2.1 振动系统模型

假设一个3自由度质量−弹簧−阻尼系统[11]，如图2所示，其中，m1=m2=m3=1 000 kg，k1=k4=40 kN/m，k2=k3=15 kN/m，c1=c4=120 Ns/m，c2=c3=45 Ns/m。上述系统的固有频率分别为f1=0.673 Hz，f2=1.180 Hz，f3=1.304 Hz，阻尼比分别为ζ1=0.63%，ζ2=1.11%，ζ3=1.23%。第2阶和第3阶模态的频率较接近。

图2 3自由度振动系统Fig.2 3-DOF representation of a mechanical system

2.2 环境振动仿真

在3个质量块上分别作用均值为0的高斯白噪声激励，模拟环境激励，计算得到3个质量块的位移响应，为了更好的模拟实际情况，对计算得到的位移响应加入零均值高斯白噪声模拟的测量噪声后作为实测振动信号。噪声水平由噪信比确定，R=σy/σx，σy和σx分别为噪声和信号的均方根值。

数值分析时，采样频率为100 Hz，采样时间为1 600 s，前200 s位移时程如图3所示，位移响应的功率谱如图4所示。

图3 质量块位移时程Fig.3 Displacement histories of m1，m2，m3

图4 位移响应的功率谱Fig.4 Power spectrum densities of the displacements

2.3 参数识别流程

采用基于解析模式分解和随机减量技术的结构模态参数识别方法开展了模态参数识别。首先，对实测信号进行功率谱分析，确定结构的频率成分；然后，进行基于解析模式分解的信号分解。二分点频率取相邻模态频率的中点0.93 Hz和1.242 Hz。为了消除实测信号中低频成分和高频成分对参数识别的影响，增加了低频和高频截止二分点频率，分别是0.3 Hz和1.60 Hz。通过解析模式分解，将信号分解成5个子信号，其中第2，3，4个子信号分别为包含第1阶、第2阶和第3阶模态频率的单模态信号，m1质量块前200 s的信号如图5所示，第1和第5个信号分别为滤除的低频和高频信号；第3步，采用随机减量技术分别对第2，3，4个子信号进行处理，获得第1阶、第2阶和第3阶模态的随机减量信号，分别如图6所示；最后，采用最小二乘法按照单自由度自由衰减振动理论函数分别拟合这3个随机减量信号，识别频率和阻尼比，拟合的自由衰减振动曲线如图6所示。

图5 AMD从m1响应中分离出来的单模态子信号Fig.5 Single-mode sub-signals decomposed by AMD

图6 RDT提取的和LSM拟合的衰减减量信号Fig.6 Random decrement signature extracted by RDT and fitted by LSM

2.4 随机减量技术参数分析

在模态参数识别过程中，影响识别结果的因素有：1)常数x0的取值；2)随机减量信号长度的选择。常数x0通常取信号均方根的a倍，即y0=a×std(y(d)i(t))。随机减量信号长度的取值与结构的阻尼比有关，当阻尼比较大时，振动很快就会衰减，过长的随机减量信号会减弱识别的精度，本文提出了随机减量信号长度取L倍模态周期的方法。进行了常数y0和随机减量信号长度最优取值分析。因系统的阻尼比差异不同，不同模态采用相同的L倍模态周期。不同a和L的参数识别结果如表1所示，识别时未加入测试噪声。常数y0取值对识别结果的影响较小，随机减量信号长度的取值对识别结果影响明显，通过分析，常数y0取1.5倍信号均方根、衰减信号长度取10倍模态周期能更准确的获得模态参数。

表1 参数a和L对识别结果的影响Table 1 Effects of parameter a and L on modal parameters identification

2.5 振动信号的选择

在环境振动动力试验时，会在不同位置布置多个测点。各阶模态在不同测点的响应与模态振型有关，因此，测点位置也会影响参数识别。分别对3个质量块的位移响应进行了模态参数识别，分析测点位置对识别结果的影响，识别结果如表2所示，由于第2阶模态振型m2的振幅为0，故m2识别的第2阶模态不准确，其他测点识别的模态参数都较准确。因此，当需要分析某阶模态的频率和阻尼比时，测点应尽可能布置在该阶模态振型位移较大的位置。

表2 由不同质量块响应识别的模态参数Table 2 Modal parameters identified by the responses of m1,m2 and m3

2.6 噪声干扰分析

分析噪声对参数识别结果的影响。取a=1.5，L=10，分析不同的噪声信比R=0，10%和20%对识别精度的影响，如表3所示，结果表明：测量噪声不影响识别结果。

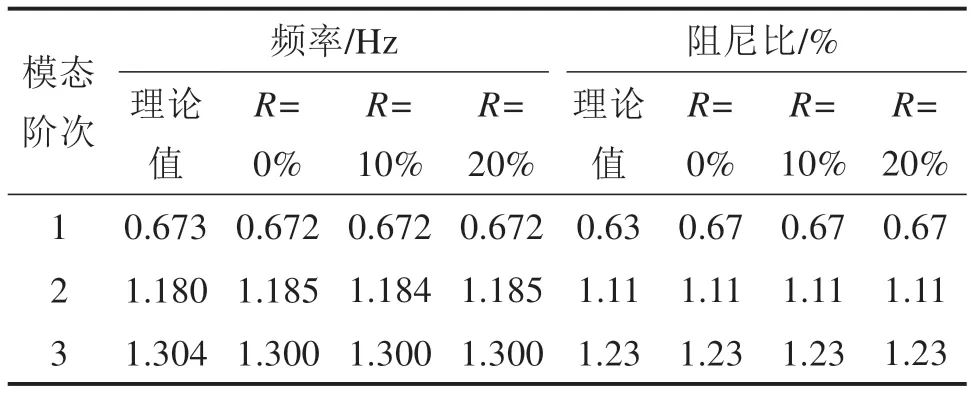
表3 噪信比R对识别结果的影响Table 3 Effects of noise to signal ratio on modal parameters identification

3 工程应用

3.1 工程概况

海心桥位于广州市新中轴线西侧，横跨珠江河。桥梁总体布置为主桥+4个引桥+接岸平台[17]。主桥为曲梁斜拱结构，拱跨为198.152 m，矢高为57.95 m，矢跨比为1/3.4，拱轴线采用二次抛物线的形式并向外倾斜10°。大桥主桥平面和立面图如图7所示。

图7 海心沙人行景观桥主桥立面和平面图Fig.7 Elevation and plan view of Haixingsha Footbridge

该桥梁位于沿海强风区，桥址周围经济发达、人口稠密，人流交通量大，因此，抗风稳定性和人致振动舒适性是该桥梁必须解决的关键问题。该桥梁为异型空间结构，主梁为曲线线型，通过有限元模态特征可知，该桥模态振型各方向耦合严重，其中第1阶和第2阶模态振型如图8所示。准确获得桥梁主要模态的频率和阻尼比对桥梁抗风性能校核和人致振动舒适度评价及减振设计至关重要。

图8 第1阶和第2阶模态振型图Fig.8 Mode shapes for the first and second mode

3.2 环境振动动力试验

为了分析人行桥主要模态的动力特征，在桥面布置了10个测点，测点布置如图9所示。因施工条件限制，结合动力试验目标，进行了3个工况的环境振动动力试验，每个工况布置8个单向拾振器，测试方向包括竖向和水平向。采样频率为100 Hz，采样时间超过1 600 s，实测加速度响应如图10所示。实测环境振动响应功率谱如图11所示。

图9 传感器测点布置图Fig.9 Instrumented sections of the accelerometers

图10 实测主梁环境激励响应Fig.10 Acceleration Responses of main girder under ambient excitation

3.3 模态参数识别

根据图11所示功率谱，确定了AMD的二分点频率，加上低频和高频滤波频率，二分点频率共5个，分别是0.50，0.80，1.12，1.38和1.80 Hz。然后对每个测点的实测响应进行相同二分点频率的AMD处理和a=1.5，L=10的RDT处理，最后对每个测点获得的4个随机减量信号进行模态参数识别。通过以上处理，每阶模态将获得多组识别参数，结合功率谱图，剔除虚假模态，最终确定合理模态参数。当某阶模态存在多个合理识别参数时，以合理识别参数的均值作为综合结果。基于AMD-RDT的模态参数识别结果如表4所示。第2阶和第3阶模态振型在1号测点处为驻点，故无法从1号测点中获得这两阶模态的信息。同时，采用随机子空间法进行了模态参数识别，识别结果也如表4所示。通过比较AMD-RDT与SSI识别的结果，两者识别的频率和阻尼比均吻合非常好，说明AMD-RDT识别的频率和阻尼比均较为可靠，可应用于实际工程。