基于孤立森林算法的风电齿轮箱轴承故障检测方法

汤婷，张岩，安宗文

(1.甘肃省特种设备检验检测研究院，兰州 730050；2.兰州理工大学 机电工程学院，兰州 730050)

风电机组大多安装在自然环境恶劣的偏远或近海地区，随着服役时间增加，大部分风电机组逐渐进入故障高发和事故频发阶段。齿轮箱故障是导致风电机组停机时间长，维修费用高的原因[1-3]。美国国家可再生能源实验室研究表明76%的齿轮箱故障由轴承故障引起[4]，因此对齿轮箱轴承进行故障检测可尽早发现隐患，保证齿轮箱安全运行以避免重大经济损失。

在工程实际中，振动信号和声发射信号常用于表征轴承状态[5-6]。在基于振动信号的轴承故障检测中，文献[7]提出了一种基于人工神经网络的风电机组主轴承故障预测方法，并具备自动报警功能；文献[8]建立了一种基于孤立森林算法的多维离群列车动车组轴箱轴承温度异常状态监测方法；文献[9]采用小波滤波对弱信号进行增强故障识别并基于自组织映射神经网络进行滚动轴承性能退化评估。除振动信号外，声发射信号对轴承故障同样敏感[10]，文献[11]针对多工况下滚动轴承故障声发射信号智能识别问题，提出了一种长短时记忆网络与迁移学习相结合的故障识别新方法。虽然声发射和振动信号对轴承的故障特征十分敏感，但相应的设备造价高昂，风电机组监测控制与数据采集系统(Supervisory Control and Data Acquisition,SCADA)大多配备的是温度传感器，在不增加外在硬件设备成本的前提下，如何有效利用丰富的温度监测数据进行故障检测成为风场关注的问题。

国内外学者以温度为出发点展开了一系列研究：文献[12]提出一种基于风电机组主轴承SCADA状态监测数据逐层编码网络的深度学习方法；文献[13]提出了一种将相关系数法、主成分分析法以及极限学习机相结合的主轴承状态监测方法；文献[14]建立了一种基于轴承温度的风电机组物理监测模型；文献[15]提出了一种利用风电机组轴承温度残差的贝叶斯推断和高斯过程的统计方法，用于预测风电机组状态。由于齿轮箱轴承通常在噪声和干扰较大的恶劣环境中工作，为提高诊断性能，需要从原始信号中提取故障敏感特征。与传统的学习方法相比，深度学习能够更好地提取特征[16-18]。

为了在不新增额外硬件成本的前提下，有效利用丰富、海量的SCADA监测数据，减少资源浪费，同时提高风电齿轮箱轴承的故障检测精度，本文以齿轮箱轴承为研究对象，温度参数为故障检测模型的输出变量进行研究。首先，使用多尺度图相关(Multiscale Graph Correlation,MGC)算法[19]选择输入变量以保证选择过程相对客观、合理；然后，采用自组织映射(Self-Organizing Map,SOM)神经网络，将提取的故障敏感特征值进行特征融合以改善输入变量的数据质量；最后，运用孤立森林(Isolation Forest,iForest)算法[20]进行异常点检测，并与多个模型进行检测精度对比，验证本模型的有效性。

1 齿轮箱轴承故障检测模型构建

如图1所示，首先，将SCADA历史运行数据进行预处理，采用MGC算法选择与输出变量——轴承温度非线性相关程度最高的9个输入变量；其次，提取输入变量的均方根和包络线并进行SOM特征融合，得到融合指标；最后，将融合指标作为样本集，以随机不放回抽取的方式构建孤立树进一步形成孤立森林，通过计算孤立树上测试样本的路径长度得出每个样本的异常分数进而判断是否为故障。

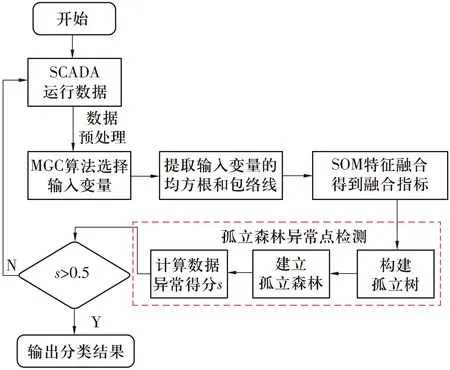
图1 故障检测流程

1.1 基于多尺度图相关算法选择输入变量

为提高风电齿轮箱轴承故障检测模型精度，需合理选择模型输入变量。MGC作为距离相关算法的推广，在非线性、多变量和噪声依赖等综合仿真上均更具优势，一个原始样本的MGC可定义为所有样本局部相关性的最大值，即

(1)

对于作为输入的一对数据集(Xn,Yn)，MGC算法的具体步骤如下：

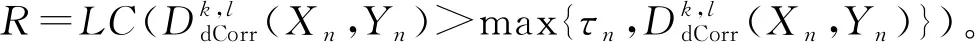
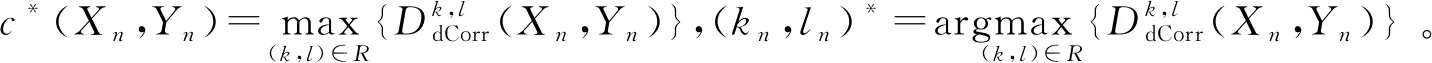
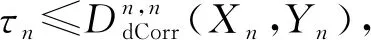
1.2 基于自组织映射神经网络的特征融合

将输入向量的故障敏感特征值进行SOM特征融合是提高齿轮箱轴承故障检测精度的关键。首先，随机设置初始权值，对m个输入神经元的连接权值赋予较小值；然后，将输入向量X=(x1,x2,x3,…,xm)T置于输入层；最后，计算映射层各神经元的权值向量和输入向量间的欧氏距离，距离计算公式为

(2)

式中：ωij为输入神经元i与映射神经元j之间的权值。将最小距离的神经元称为最佳匹配单元；然后更新最佳匹配单元的权重向量及其拓扑邻域，使其在输入空间中更接近输入向量。其中，输入向量在映射层形成一组一维融合值，用最小量化误差[21](Minimum Quantization Error，MQE)表示为

eMQE==X-mBMU=，

(3)

式中：X为输入数据向量；mBMU为最佳匹配单元的权重向量。eMQE值越小，表明当前齿轮箱轴承状态离基准健康状态越近；反之则越可能接近故障状态。

1.3 基于孤立森林算法的异常点检测

孤立森林算法无需计算样本之间的距离，实现简单且可快速区分出异常数据，对群体异常数据以及离散异常数据都有很好的检测能力。

1.3.1 构建孤立树

1.3.2 建立孤立森林

设定孤立树的限制高度l近似于平均高度，l与子样本数量ψ的关系为l=ceiling(log2ψ)，当孤立树生长至平均高度即停止，n棵互不影响且相互独立的孤立树组成孤立森林。孤立森林算法的构建过程为：首先，初始化孤立森林，设置孤立树最大高度l=ceiling(log2ψ)；然后，在待监测样本集X中随机抽取容量为ψ的样本集，将采样样本放入集合X′并将X′作为根节点，按照孤立树算法得到孤立树；最后，将孤立树放入孤立森林。

1.3.3 确定路径长度

样本点x的路径长度h(x)为从孤立树的根节点到叶子节点所经过的边的数量。路径长度越短隔离敏感性越高，反之则越低。h(x)的计算步骤为：如果测试样本点x是叶子结点或树的当前高度h大于其最大高度l，则返回至h+c(T)；如果xq≤p，则返回至路径长度PathLength(x,Tleft,h+1)处，反之则返回至路径长度PathLength(x,Tright,h+1)处。

孤立森林算法进行异常检测的本质是将被检测点的反应异常程度进行排序，根据样本点的路径长度计算异常得分。排序越靠前，得分越高。异常点得分s定义为

(4)

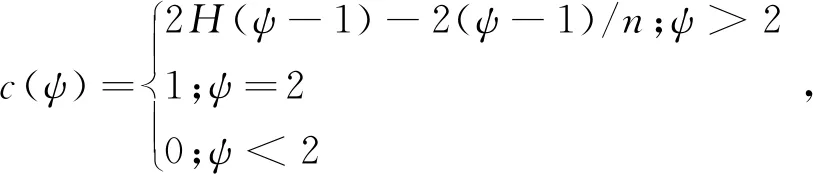
(5)

H(n)=lnn+ε，

式中：h(x)为待检测样本x在孤立树中的路径长度；E[h(x)]为h(x)的期望值；c(ψ)为孤立树的平均路径长度；ψ为子采样大小；n为T的根节点所包含的样本量；H(n)为调和函数；ε为欧拉常数，ε=0.577 215 664 9。

根据s与E[h(x)]的关系确定异常点判定方法：当E[h(x)]→c(ψ)时，s→0.5，无法判定是否异常；当E[h(x)]→0时，s→1，判定为异常；当E[h(x)]→n-1时，s→0，判定为正常。其中，异常点得分0≤s≤1。

2 齿轮箱轴承故障检测模型验证

风电机组SCADA数据具有丰富的类型和海量的存储，但由于系统技术不成熟或其他环境因素导致有用信息十分匮乏，仅根据历史运行数据(表1)无法判别是否故障以及何处发生故障。因此，为保障风电机组的故障检测、诊断与预测精度，需借助数据挖掘技术及其相应算法从原始数据中获取有效信息和优质数据。

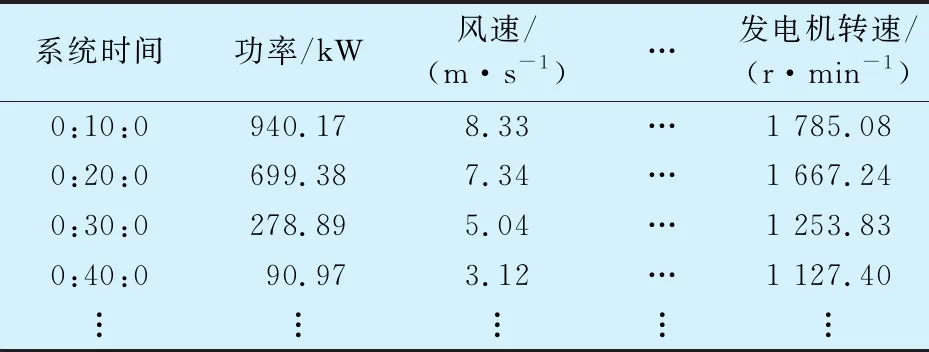
表1 SCADA原始数据样式

2.1 轴承故障监测点

SCADA系统可对齿轮箱的轴承温度、润滑油温度等参数进行监测和记录。配置有不同轴承的3级行星齿轮箱如图2所示[22]，其中A和B分别为行星齿轮架两端轴承。C，D和E分别为齿轮箱高速轴上的轴承。本文选取的齿轮箱轴承温度监测点是位于齿轮箱高速轴靠近发电机侧的轴承E。

图2 齿轮箱轴承位置示意图

2.2 选择输入变量

根据SCADA数据可以绘制风电机组各参数随时间的变化以及不同参数之间的相互关系图。齿轮箱轴承温度的变化以及有功功率与风速之间的关系如图3、图4所示，SCADA参数自相关和互相关均成非线性且复杂的关系，难以直接定性分析或得出明确物理关系。

图3 齿轮箱轴承温度

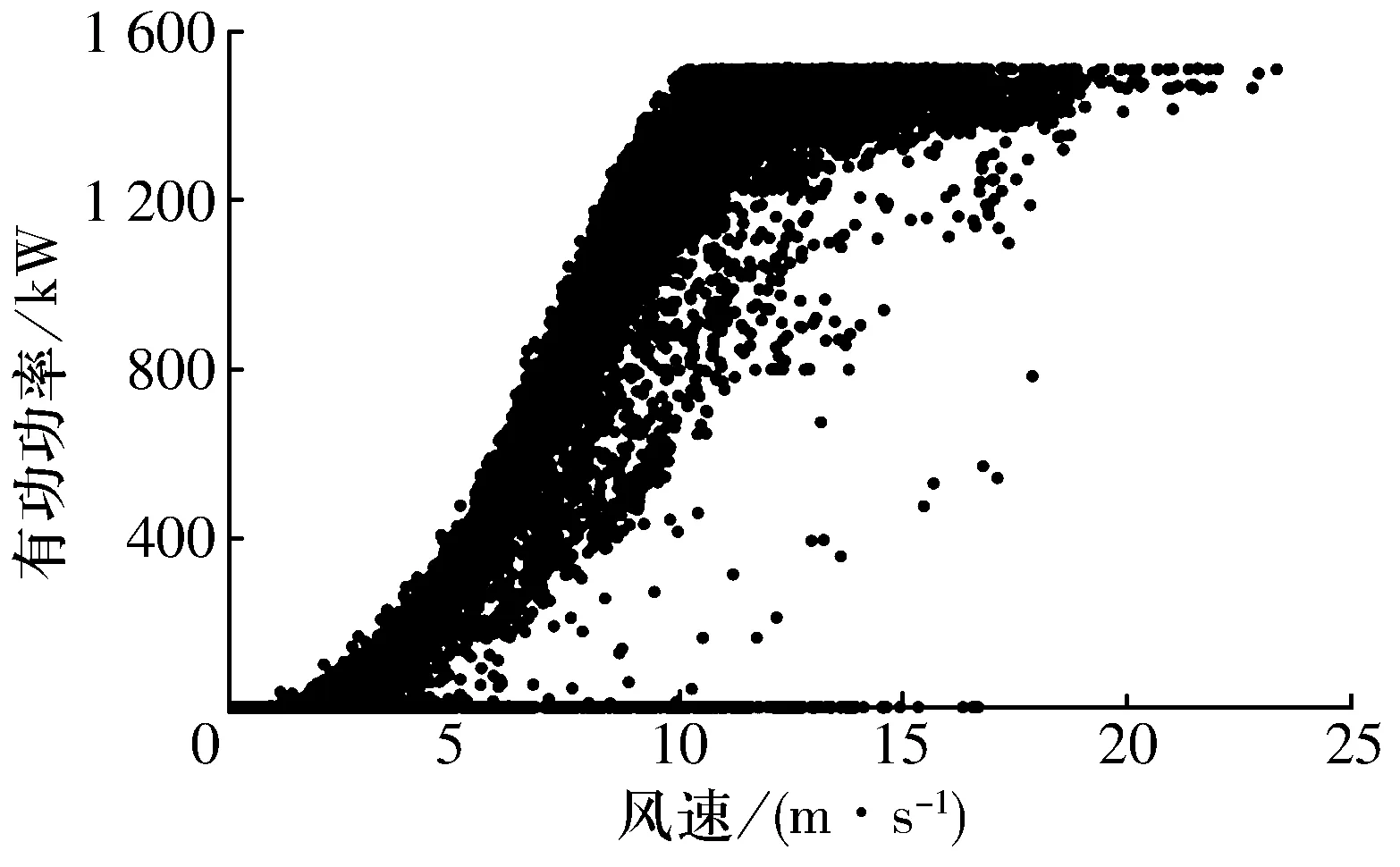
图4 风速-有功功率

为避免因人工选择或线性相关算法导致的主观臆断或参数选择不合理，采用MGC算法选择与轴承温度非线性相关程度较高的参数,结果见表2，从中选择前9个非线性相关程度较高的参数作为轴承故障检测模型的输入变量。

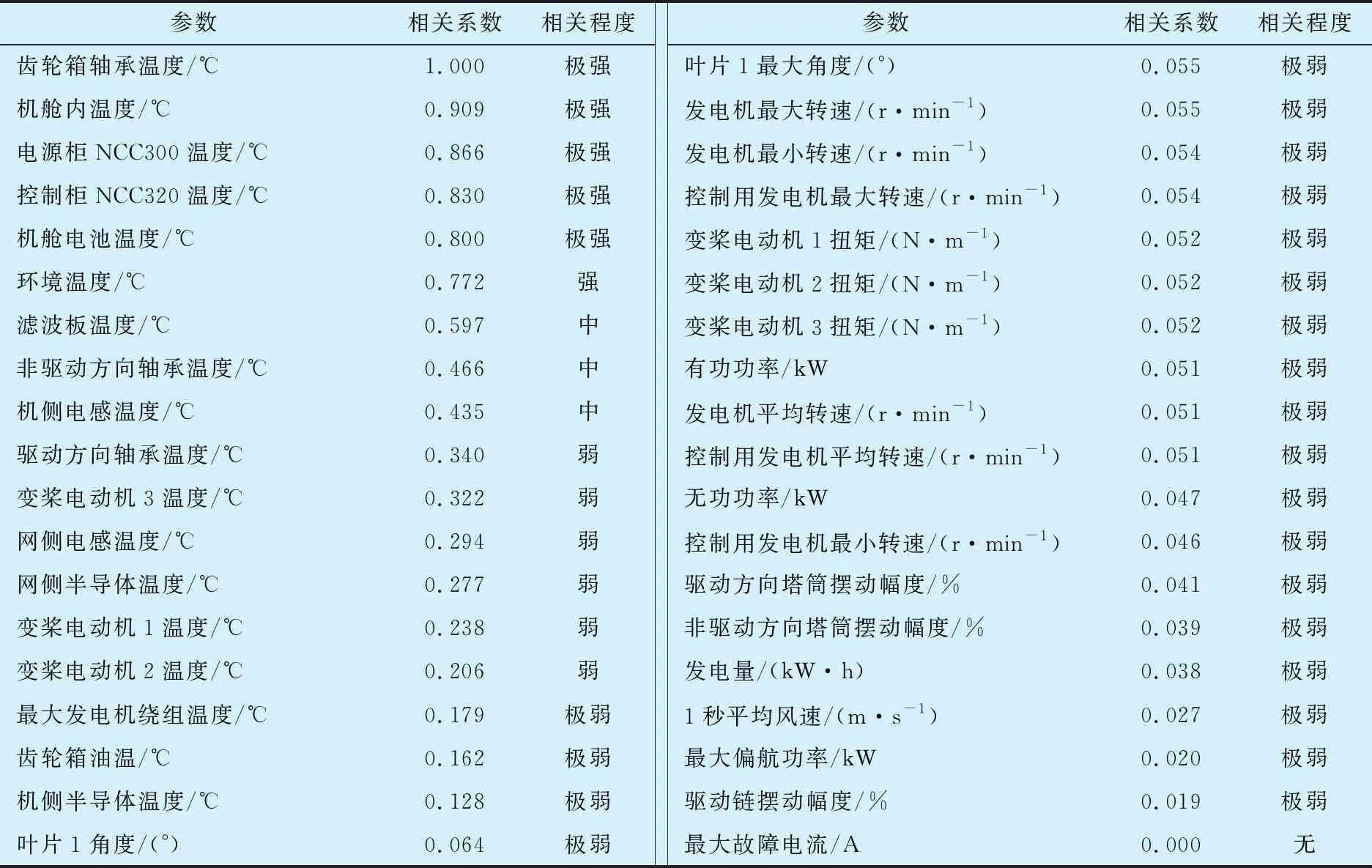
表2 轴承温度与输入变量的相关程度

2.3 输入变量进行SOM特征融合

为进一步提高故障检测的性能和精度，从9个输入变量中分别提取均方根和包络线这2种故障敏感特征，并将其进行SOM特征融合，使故障趋势更为明显。以输入变量电源柜NCC300温度为例，其均方根和包络线如图5所示，经过SOM特征融合后得到的最小量化误差如图6所示，由图可知电源柜NCC300的温升异常且有3处超过阈值。

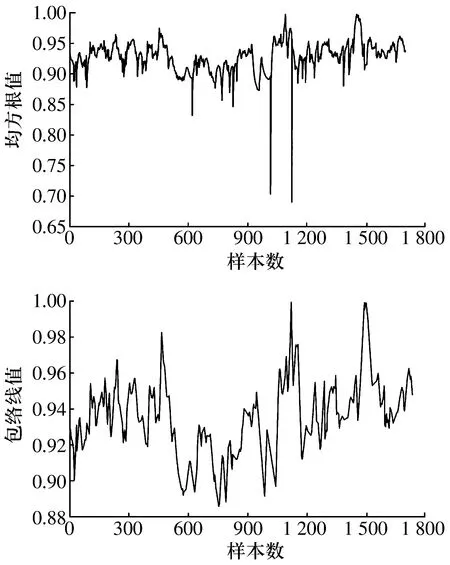
图5 电源柜NCC300温度的均方根和包络线

图6 电源柜NCC300温度的最小量化误差

阈值根据输入变量正常范围的上限值确定，即在数据样本最后处设置上限值，将其一同按照数据处理步骤进行处理，最终得到的位置即为阈值，图6中电源柜NCC300温度的阈值约为1.1。由于不同输入变量的正常范围值不同，因此均需与样本点一同做量纲一化预处理。由于风速长时间小于切入风速导致风电机组停机，风速虽已慢慢超过3 m/s，但为保护风电机组，仍处于停机保护状态而非故障停机。

进一步，将所有输入变量的均方根和包络线进行SOM特征融合，即输入变量由3 400×9组原始数据变为1 700×1组融合值最小量化误差eMQE，融合结果如图7所示。将9组输入变量进行特征融合后，故障异常点明显，超过阈值的异常点一共有4处，其中所有输入变量融合值的阈值约为1.0。

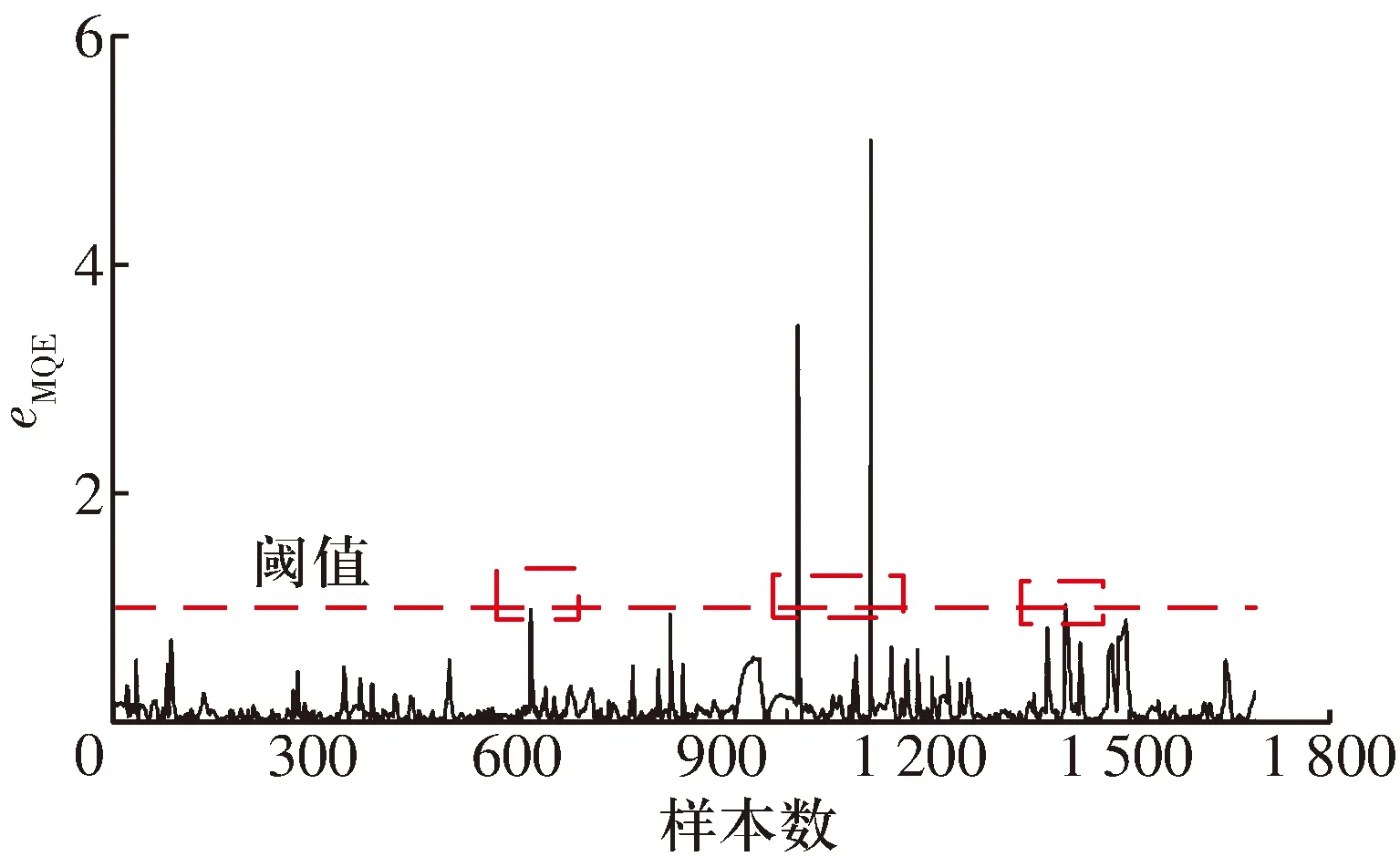
图7 所有输入变量的最小量化误差

2.4 基于孤立森林算法的故障检测

基于孤立森林算法的异常值检测方法可将数据样本的特征通过无监督学习方式存储在森林中，稳定性高且能准确检测出数据样本中的异常值，因此以孤立森林算法作为齿轮箱轴承故障检测的核心算法，其流程如图8所示，具体步骤如下：

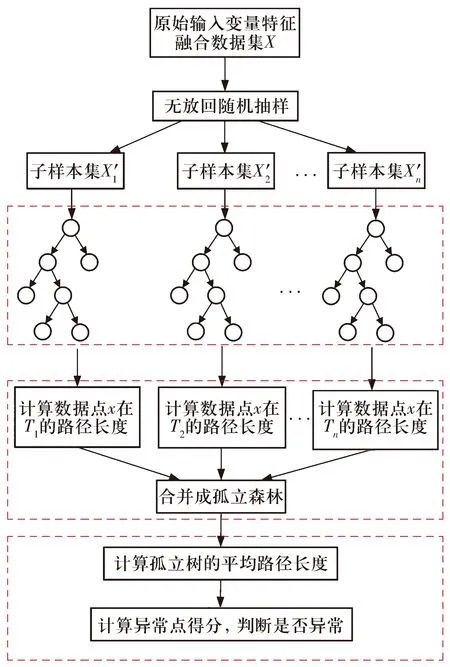
图8 基于孤立森林算法的齿轮箱轴承故障检测流程图

1)建立输入变量的特征融合数据集X′，SOM融合指标eMQE为数据集第1列，对应的标签为第2列，正常和异常数据点分别以“0”和“1”作为标签，共1 700条。由于异常点仅有4处，在数据集中占比太小，故人为加入260组异常值以平衡数据比例。

2)采用随机不放回取样方式，抽取n个训练子样本构建孤立树，合并成孤立森林。孤立森林中孤立树为100棵，每棵树所含的样本数为256。

3)计算每个子样本集中的数据点在孤立树中的路径长度，并计算孤立树的平均路径长度。

4)综合所有数据点的路径长度，计算相应的异常点得分，判断是否异常。

3 算例分析

考虑到西北地区的四季气温变化巨大，为保证模型精度，以2013年3月23日至4月底甘肃某风场第56台风电机组的SCADA数据作为研究对象，该数据每10 min记录一次，共包含38个监测参数，共计3400×38组。风电机组在3～20 m/s的风速范围内正常运行和发电，当小于切入风速(3 m/s)时，风电机组处于停机状态；当大于额定风速(20 m/s)时，会因转速过快损伤风电机组。因此首先剔除风速范围外的相关参数，同时对SCADA数据进行量纲一化处理以消除各参数变量的量纲和数量级不一致问题，以更好地研究各参数间相关关系。

取包含自然异常点的4月15日11点30分、4月17日21点20分、4月17日21点30分和4月25日17点20分共4组数据进行故障检测，根据上述训练过程得到的基于孤立森林算法的异常点检测结果如图9所示，基于孤立森林算法的风电齿轮箱轴承故障检测方法准确识别出了4个自然异常点。

图9 某风场风电齿轮箱轴承故障检测结果

为验证基于孤立森林算法的风电齿轮箱轴承故障检测方法的有效性，在使用相同数据集的前提下，分别采用反向传播神经网络(BPNN)、随机森林(RF)和支持向量机(SVM)进行齿轮箱轴承故障检测，各检测模型的参数见表3。

表3 各检测模型的参数选取

每种模型测试10次后取平均值表征其检测性能，检测结果见表4，孤立森林算法的故障检测平均精度为100.0%，平均运行时间为0.207 s，整体表现最优。

表4 故障检测模型效果对比

为验证SOM特征级融合的有效性，将量纲一化后的输入变量直接进行10次孤立森林算法异常点检测，SOM融合前、后模型的检测性能如图10所示。曲线下的面积可以表征精度，明显发现数据融合后的面积更大，说明其检测精度更高。定量分析得到SOM融合前的平均检测精度为78.44%，平均运行时间为0.330 s。因此，对输入变量进行SOM特征级融合处理后，平均检测精度提高21.56%，平均运行时间缩短0.123 s。

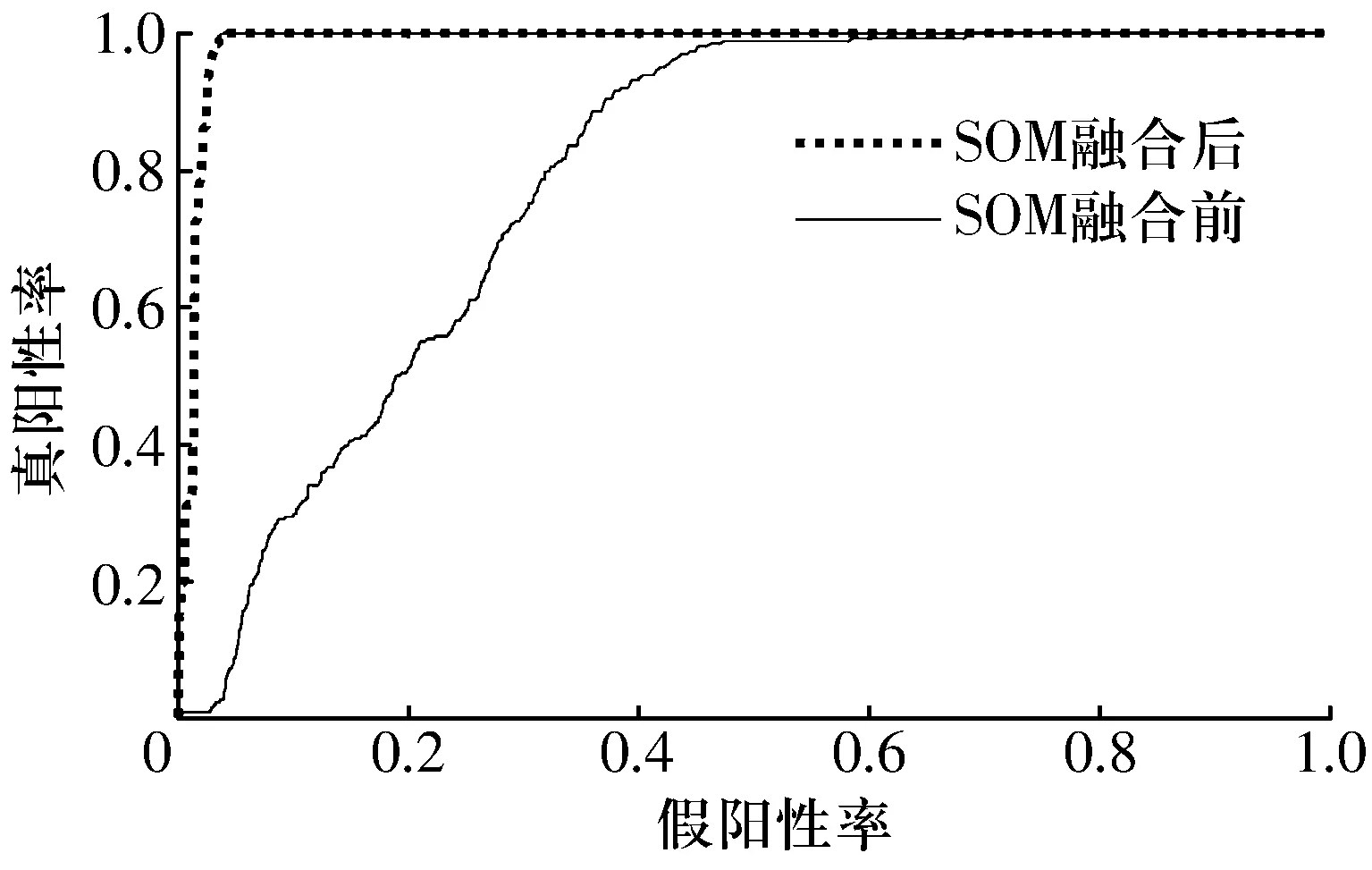
图10 孤立森林算法检测性能对比图

4 结束语

以风电齿轮箱轴承为研究对象，引入MGC算法选择输入量，采用SOM神经网络特征融合获得输入值eMQE，构建了一种基于孤立森林算法的风电齿轮箱轴承故障检测方法。本方法可在不新增外部硬件的前提下，通过一段关键部件的历史运行数据准确获取故障信息。与BPNN，RF，SVM模型相比，本方法综合性能最优,采用信息融合技术使检测时间缩短了0.123 s，检测精度提高了21.56%。