以高压CO2为介质的推力箔片轴承静特性分析
2022-06-08车国铚杨启超张克龙高志成
车国铚,杨启超,张克龙,高志成
(1.青岛科技大学 机电工程学院,山东 青岛 266061;2.中国船舶重工业集团公司 第719研究所,武汉 430064;3.广东智空动力科技有限公司,广东 佛山 528216)
超临界二氧化碳布雷顿循环作为传统蒸汽动力循环的替代方案,使用超临界区的CO2作为循环介质,比氦气布雷顿循环以及蒸汽朗肯循环的效率更高[1],而且超临界二氧化碳(S-CO2)的密度更大,使系统设备尺寸减小,具有良好的经济性,因此在核电、火电、太阳能发电等能源利用领域具有良好的发展前景[2]。
压缩机作为超临界二氧化碳布雷顿循环中的核心关键设备,其安全高效运行对布雷顿循环效率有至关重要的影响。对S-CO2压缩机及其关键轴承零部件的设计是目前透平机领域研究的热点[3]。
目前,对推力箔片轴承的研究多以空气为润滑介质,而对采用较高压力的CO2为润滑介质的研究较少,且性能还没有太多明确的结果[4]。与空气相比,高压CO2为润滑介质对预测和计算箔片轴承的性能提出了新挑战,如湍流状态、非线性热力学性质等,这成为研究高压CO2推力箔片轴承性能的动机,也成为近年气体轴承研究的热点[5]。
国外对S-CO2布雷顿循环压缩机中气体轴承的研究较早,主要包括承载力、温度特性、摩擦功耗等,而国内近几年才开展研究。文献[6]率先搭建功率为250 kW的试验台研究压缩机中采用CO2直接润滑的气体轴承,在压缩回路中通过热敏电阻测得推力轴承出口处气体温度为15~37 ℃,指出转子腔的压力应设计在2 MPa以下,理想情况约为1.4 MPa,以降低转子和气体轴承的风阻损失。文献[7]在高达4.8 MPa的CO2中单独运行气体箔片轴承,研究其在高压CO2中的功率损失,结果表明气体箔片轴承的功率损失随CO2压力的增加而增大。文献[8]考虑真实气体效应和薄膜内流动湍流状态,对混合推力轴承进行了三维热流体动力学分析,计算了一定尺寸推力轴承的压力分布、承载力、功率损失等。文献[9]采用计算流体动力学的三维流体结构模型,研究了高压CO2箔片推力轴承的弹性流体动力性能和运行条件对其性能的影响,比较了不同流动状态下箔片推力轴承性能的变化。文献[10]在连续性方程和动量方程的基础上推导层流状态下适用于S-CO2径向轴承的雷诺方程,并考虑湍流速度脉动的影响,在雷诺方程中加入修正系数,采用差值法获得S-CO2物性,并用有限差分数值法初步计算了推力气体轴承的静态性能,但未分析工况及结构参数对径向气体轴承静特性的影响。
本文考虑CO2的实际物性及湍流状态对润滑气膜的影响,运用有限差分法数值求解流体润滑雷诺方程,分析结构及工况参数对推力箔片轴承性能的影响,并与空气为工作介质的轴承性能进行对比。
1 推力箔片轴承结构
8个瓦块的推力箔片轴承示意图如图1所示,其中R1为轴承内半径,R2为轴承外半径,β为扇形瓦张角,b为节距比,表示平箔楔形部分占整个瓦块的比例,δh为楔形面高度,h2为平箔水平面与推力盘之间的间隙,也称最小气膜厚度,h1为楔形部分与水平面部分高度的和。瓦块上的每个点都可以用径向方向上的半径长度r和圆周方向上的角度θ表示,lin和lout分别为进气口和出气口。

图1 推力箔片轴承结构示意图
通常,平箔和波箔的一端通过点焊固定在轴承座上。平箔由楔形部分和水平部分组成,与推力盘表面之间形成楔形间隙。转子运行过程中气体被吸入推力盘与推力轴承的间隙,沿间隙变小的周向方向运动,形成动压效应并产生一定的承载力以平衡轴向力。与滚动轴承相比,气体箔片轴承具有摩擦功耗小的优点,在转子受到不稳定涡动时,通过具有柔性支承的弹性箔片之间的相互作用吸收部分涡动能量,使转子运行稳定[11]。
2 数学模型及求解
2.1 变密度变黏度湍流雷诺方程
考虑密度、黏度变化以及高压状态下湍流状态对润滑气膜的影响,修正雷诺方程为
(1)

为简化计算,对(1)式量纲一化,令

(2)
式中:pa为轴承外部环境压力;μa为轴承外部环境下CO2的动力黏度;ρa为轴承外部环境下CO2的密度。
(1)式变为
(3)
2.2 气膜厚度方程
假设推力盘无倾斜时,每个扇形瓦块结构相同,因此每个扇形瓦块之间润滑气膜的厚度分布相同。气体箔片轴承工作时,箔片的弹性变形会影响轴承的气膜厚度,数值分析时需考虑箔片的弹性变形。本文所采用的弹性箔片结构如图2所示,s为波箔单元长度,tb为波箔厚度,tp为平箔厚度,l为波箔波纹直径。本文采用经典Heshmat模型,不考虑平箔的刚度,忽略弹性箔片之间的相互摩擦作用以及波箔与轴承座的摩擦,则箔片刚度kb为[12]

图2 波箔和平箔结构
(4)
其量纲一化为
(5)
式中:Eb为波箔材料的弹性模量;νb为波箔材料的泊松比。
对于弹性箔片轴承,润滑气膜厚度为
h=h2+g(θ)+u(r,θ),
(6)
式中:g(θ)为间隙内的润滑气膜厚度;u(r,θ)为弹性变形量。
对h2,g(θ),u(r,θ)分别进行量纲一化,令
(7)
(6)式变为
(8)
2.3 变密度变黏度湍流雷诺方程的数值求解
采用有限差分数值法将扇形瓦块的计算域离散为差分网格,用有限个网格节点替代连续的求解域,润滑气膜展开为m×n的离散网格(图3),图中Δθ,Δr分别为周向和径向的网格间距,i,j分别为周向和径向的网格节点编号。
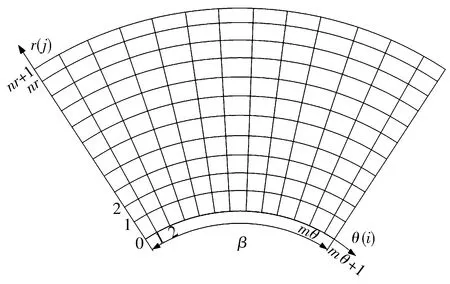
图3 计算域网格划分示意图
基于有限差分法,采用计算精度较高的中心差商,将控制方程中周向和径向的压力偏导数用相邻节点函数值的中心差商近似表示,即
(9)
根据(9)式对(3)式进行离散化。
(3)式左边第1项离散为
(10)
(3)式左边第2项离散为
(11)
由于静态计算无需考虑时间项,因此(3)式右边第一项离散为
(12)
将(10)—(12)式代入(3)式得
pi,j=
(13)
(14)
扇形瓦块的每个边界都与外界环境接触,因此每个边界都为外界环境条件,故有
(15)
为加快迭代计算过程的收敛速度,采用松弛迭代法进行计算,迭代格式为
(16)
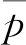
采用相对收敛准则判断迭代是否达到精度要求,达到精度要求后终止迭代。本文相对收敛准则参照文献[11]选取,即
(17)
2.4 计算对象及方法
2.4.1 计算对象
采用文献[13]中空气循环机推力箔片轴承尺寸,确定推力箔片轴承结构参数见表1。
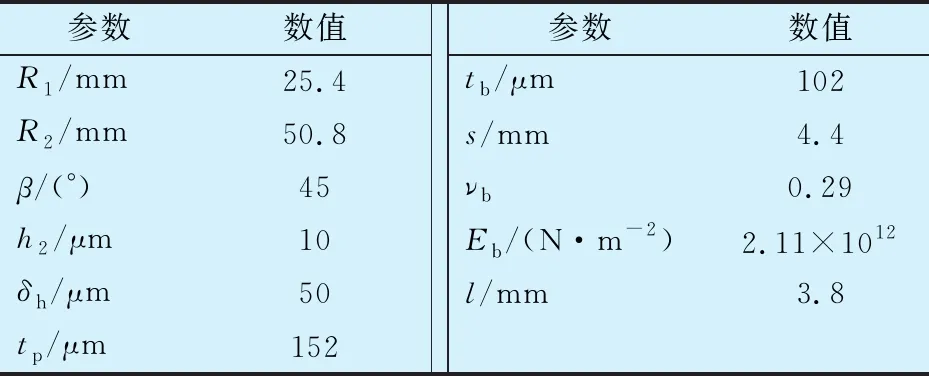
表1 推力箔片轴承结构参数
2.4.2 密度和黏度处理方法
采用NIST Refprop 软件获取CO2流体热物性,不同温度及压力下的密度、黏度都可通过软件编程调用。
2.4.3 计算流程
整体迭代计算流程如图4所示。

图4 气膜压力计算流程图
2.5 静态性能计算
联立(3)和(8)式,获得楔形间隙内润滑气膜的压力分布,在轴承计算区域对其积分得到承载力和摩擦力矩。
(18)

(19)
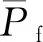
(20)
3 数值结果及分析
3.1 计算程序验证
根据图4的计算流程,用MATLAB编写数值计算程序。以CO2为润滑介质的推力轴承研究较少,本文计算空气作为润滑介质的刚性表面与弹性表面的轴承性能,并与文献[15]的数据进行对比,结果见表2。计算数据为量纲一的值,k为0时为刚性表面,h1/h2为气膜间隙比。由表2可知最大误差为7.14%,验证了本文所用计算程序的准确性。
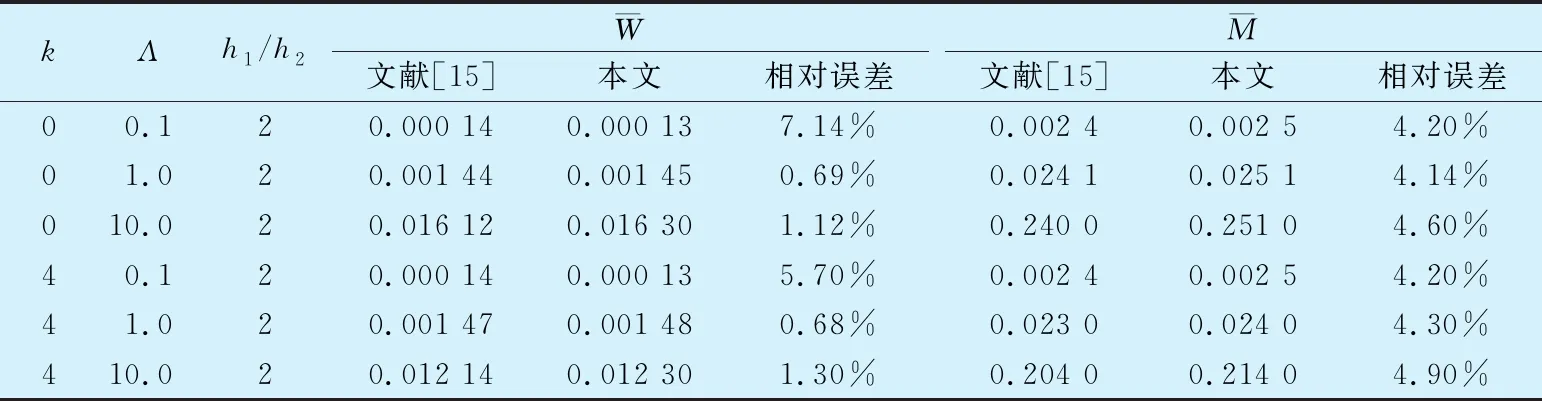
表2 本文与文献[15]计算结果对比
3.2 推力轴承静态性能计算结果
转速n为40 000 r/min, 环境温度T为300 K,pa为1.4 MPa时,CO2为润滑介质的推力箔片轴承气膜压力和厚度分布分别如图5和图6所示。图5中压力沿扇形瓦气流进口到出口方向先增大后减小,在倾斜面与水平面的交界处附近达到最大,CO2气膜压力峰值为1.5 MPa,各边界处压力为环境压力;图6中气膜厚度在径向方向上恒定,最终在气流出口降至环境压力。以图5气膜压力的计算结果为基础,计算得到承载力为344.88 N,摩擦功率损失为108.2 W。

图5 高压CO2推力箔片轴承气膜压力分布
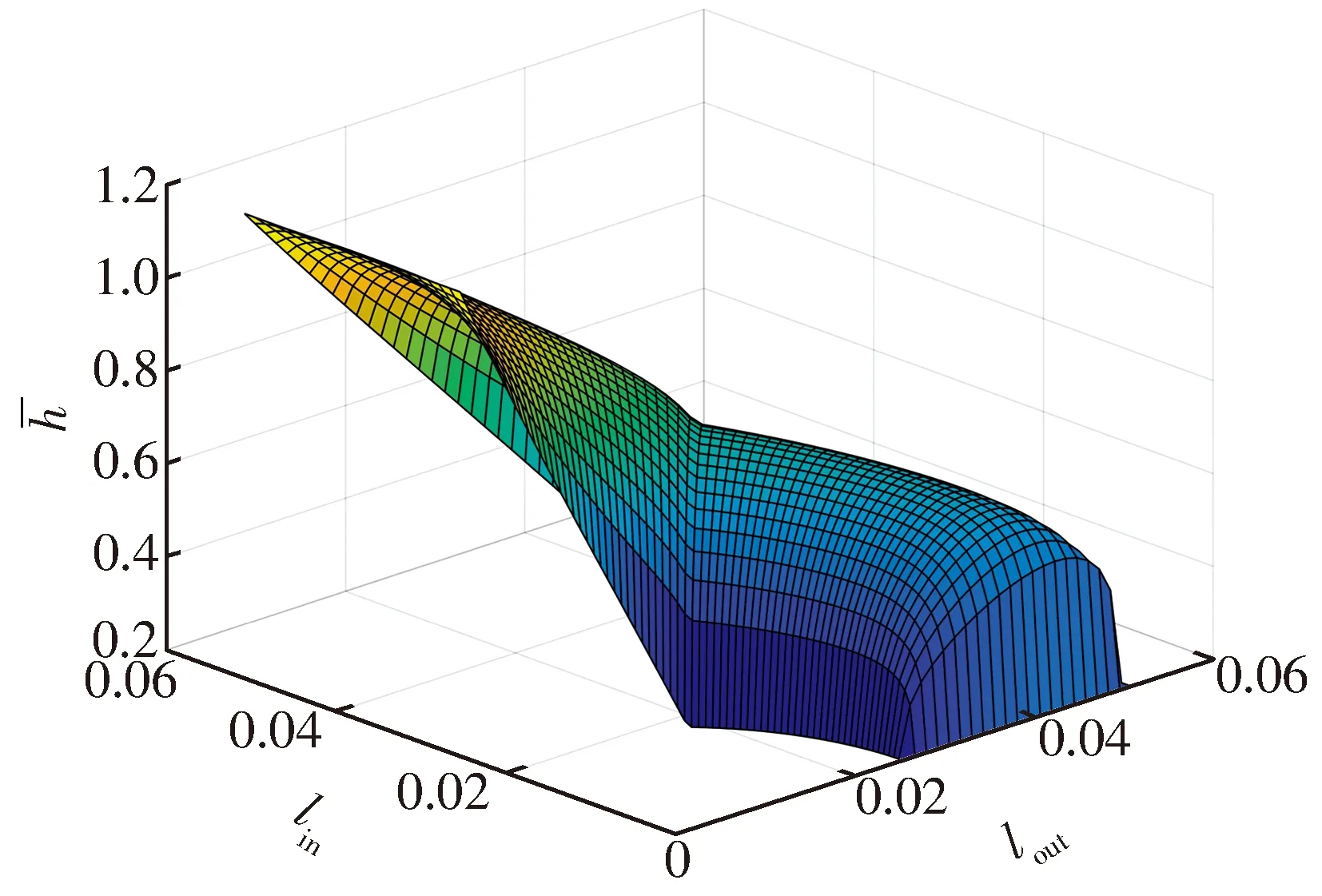
图6 高压CO2推力泊片轴承气膜厚度分布
T为300 K,pa为1.4 MPa,不同转速下瓦块径向中截面处的气膜压力分布如图7所示,随转速升高,气膜压力呈增大的趋势。

图7 高压CO2时扇形瓦块径向中截面处气膜压力曲线
采用同一推力箔片轴承,分别计算高压CO2与空气为润滑介质时扇形瓦块径向中截面处气膜厚度曲线如图8所示,在相同转速下,高压CO2为润滑介质时的气膜厚度远大于空气,说明高压CO2使弹性箔片发生了较大的变形;在不同转速下,高压CO2的轴承气膜厚度差异较大,而空气时差异较小。
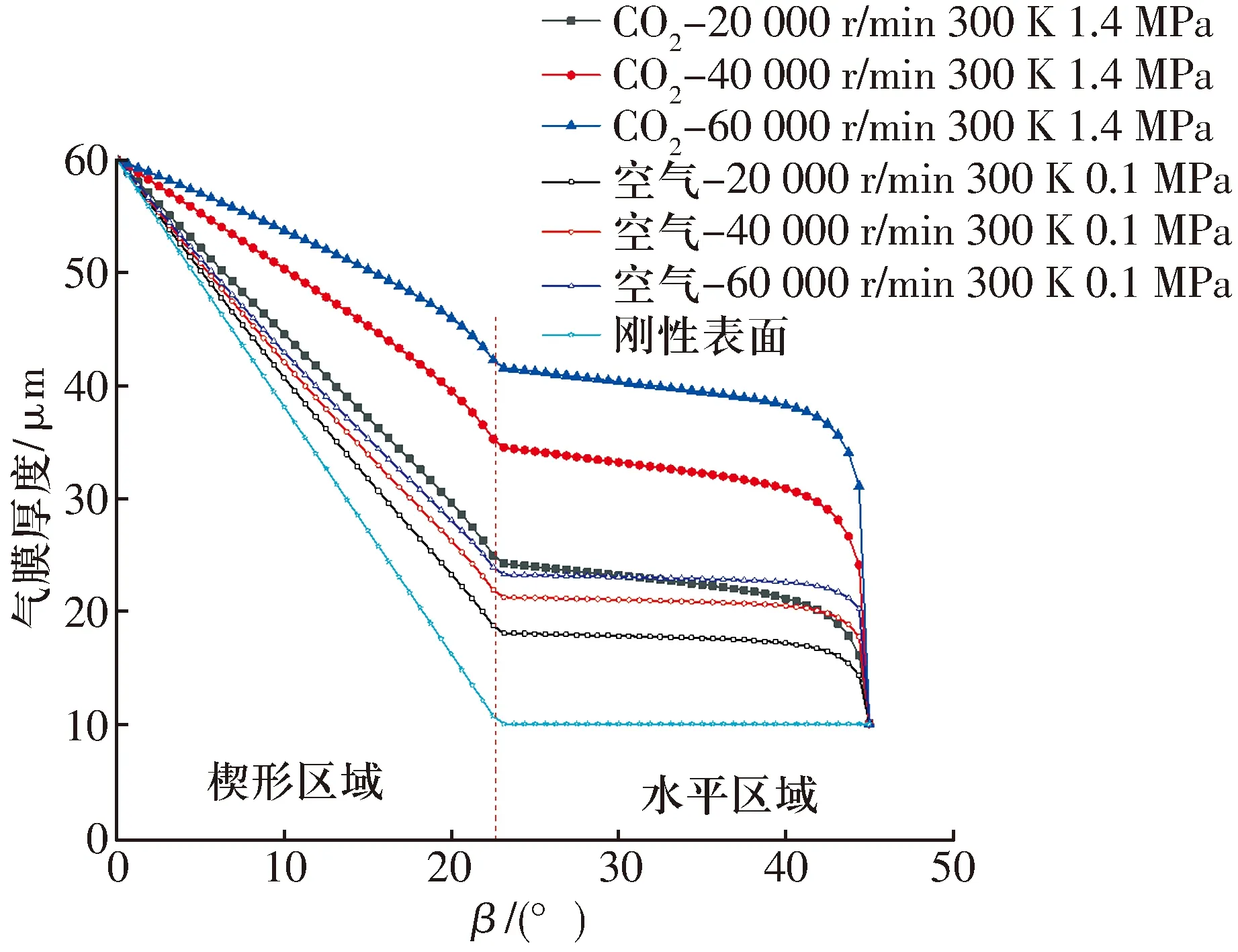
图8 高压CO2与空气时扇形瓦块径向中截面处气膜厚度曲线
空气与高压CO2作为润滑介质时的承载力对比如图9所示,空气产生的承载力远小于高压CO2产生的承载力;随转速提高,空气产生的承载力变化较小,而对应的高压CO2变化较大;空气润滑介质轴承承载力仅为1.4 MPa下CO2润滑介质轴承承载力的41%。

图9 高压CO2与空气时轴承承载力对比
3.3 节距比对推力箔片轴承静态性能的影响
桑迪亚国家实验室的压缩机设计最高转速为75 000 r /min,故以此为参考,n为75 000 r/min,T为300 K,pa为1.4 MPa时,不同扇形瓦张角下推力箔片轴承瓦块节距比与轴承承载力的关系如图10所示,随节距比增大,轴承承载力呈先增大后减小的趋势。
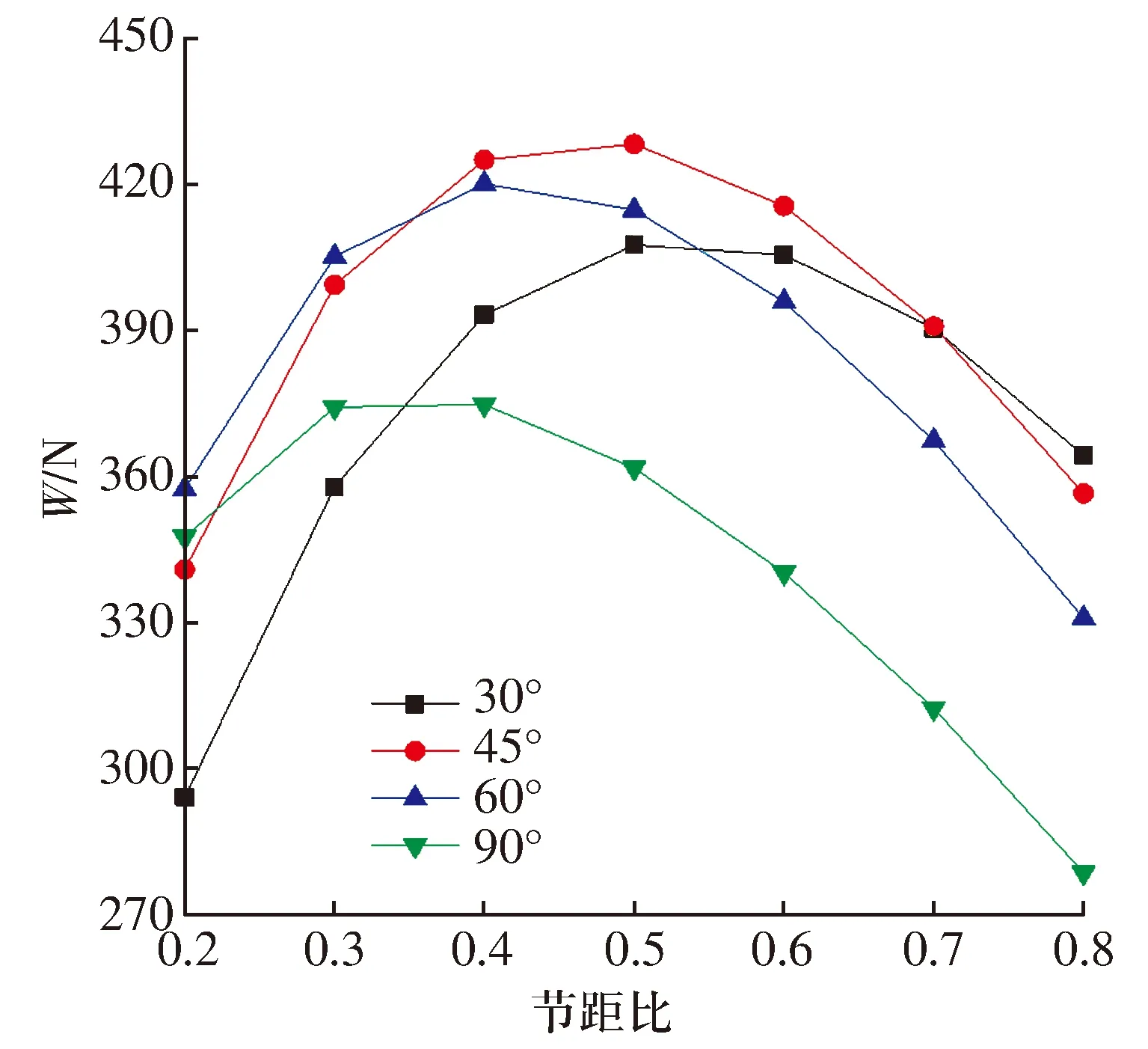
图10 不同瓦张角下节距比对轴承承载力的影响
定义达到轴承最大承载力时的节距比为最佳,由图10可知,最佳节距比随扇形瓦张角的增大而减小,轴承最大承载力随扇形瓦张角的增大呈先增大后减小的趋势,本文计算条件下当扇形瓦张角为45°时轴承承载力出现了最大值,约为429.5 N,反映不同节距比时,轴承最大承载力对应的最佳瓦张角不同。
推力箔片轴承的摩擦功耗与节距比的关系如图11 所示,摩擦功耗随节距比增大呈先增大后减小的趋势,这是因为轴承的摩擦功耗与气膜压力直接相关,与图10中轴承承载力的变化规律一致。当扇形瓦张角较小,即设计更多的瓦块时,间隙内气膜与推力盘摩擦导致的摩擦功耗越大。当推力箔片轴承的瓦张角为30°、节距比为0.5时,摩擦功耗接近600 W,当转速继续提高时,摩擦功耗继续增大。

图11 不同瓦张角下节距比对摩擦功耗的影响
由图10和图11可知,扇形瓦张角为45°、节距比为0.5时轴承承载力较大、摩擦功耗较小,因此本文后续数值分析计算采用此条件。
3.4 楔形高度对轴承静态性能的影响
固定最小气膜厚度h2为10 μm,研究不同楔形高度对轴承承载力的影响(图12),楔形高度反应了楔形间隙倾斜角的大小,楔形高度逐渐增大,即斜面倾斜角逐渐增大时,轴承承载力先增大后减小;当其他条件固定时,转速为70 000 r/min时达到轴承最大承载力;随转速提高,轴承最大承载力对应的楔形高度有增大的趋势。
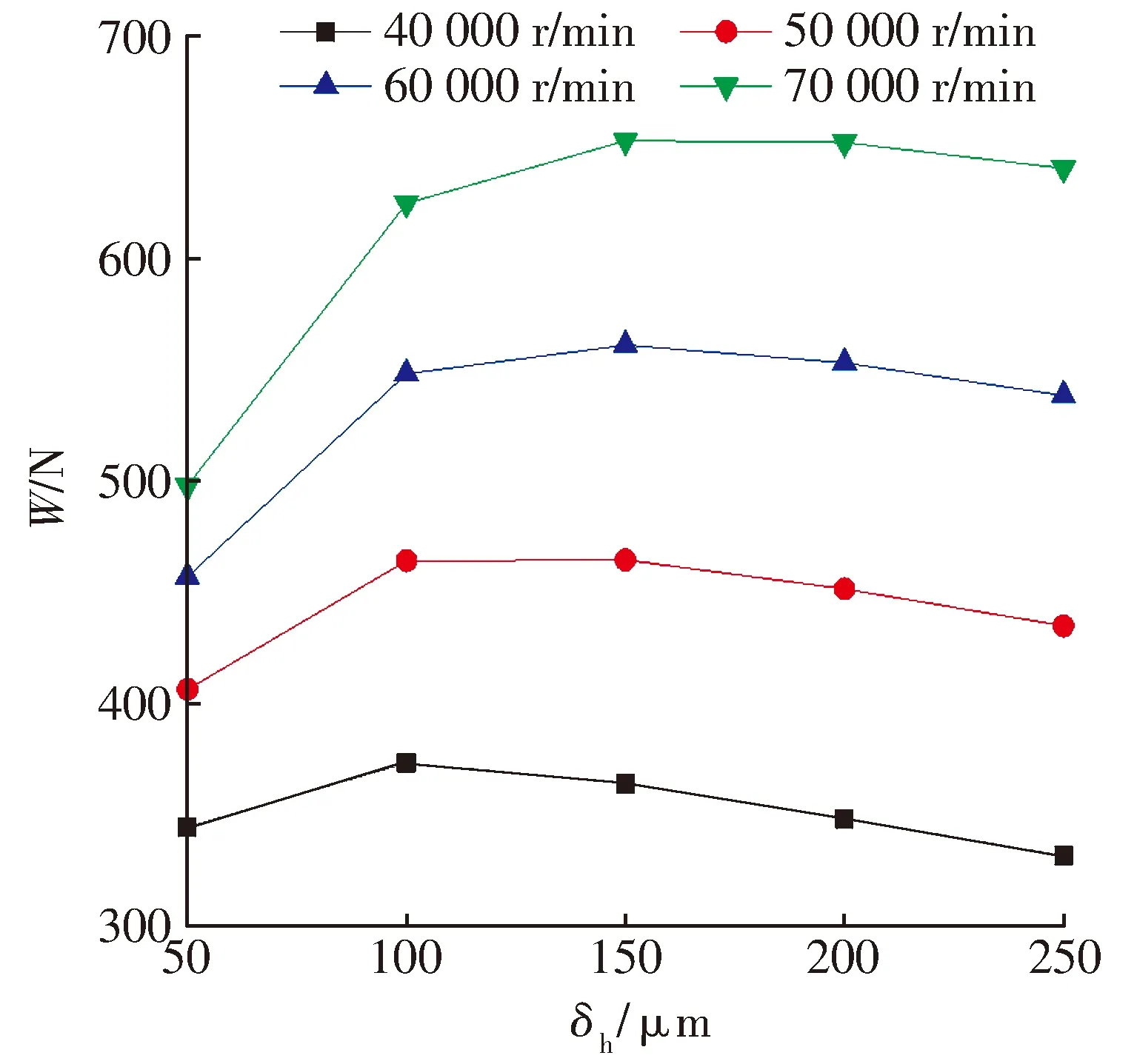
图12 不同转速下楔形高度对承载力的影响
轴承在不同楔形高度和转速下的摩擦功耗变化规律如图13所示,摩擦功耗随着楔形高度的增大而逐渐增大,且高转速、大楔形高度对应的摩擦功耗较大。

图13 不同转速下楔形高度对摩擦功耗的影响
当n为40 000 r/min,T为300 K,pa为1.4 MPa时,不同楔形高度对应的扇形瓦块径向中截面压力分布如图14所示,随着楔形高度的增大,轴承水平区域压力呈先增大后减小的趋势,楔形区域气膜压力呈下降趋势。楔形高度增大使楔形区域气膜压力降低,此区域轴承承载力减小,承载任务主要集中在水平区域,将加剧该区域的摩擦,不利于水平区域的工作。

图14 不同楔形高度下扇形瓦块径向中截面压力分布曲线
假设楔形高度以50 μm为初始参考值,楔形高度分别设计为100,150,200,250 μm时,楔形区域气膜压力达到与50 μm设计条件下相同值的瓦张角分别约为13°,17.5°,19°,21°,瓦张角有后移现象,如图中红色圆圈所示。分析其原因为推力箔片轴承的楔形高度对动压效应具有重要作用,当楔形高度增大时,动压效应的产生区域会从入口向右移动。
3.5 最小气膜厚度对轴承静态性能的影响
推力箔片轴承的楔形高度通常在设计时已固定,即轴承结构参数已确定,而推力箔片轴承与推力盘间隙的最小气膜厚度h2在装配以及实际工作过程中随着轴向力的变化而变化。固定楔形高度为50 μm,不同转速下最小气膜厚度变化对轴承承载力和摩擦功耗的影响分别如图15和图16所示。
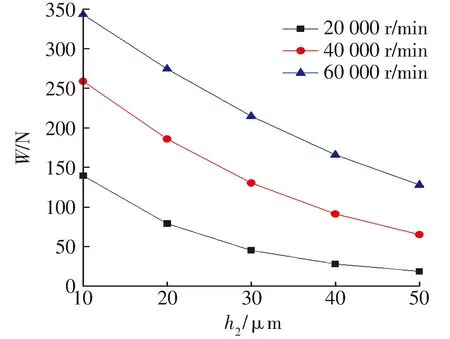
图15 不同转速下最小气膜厚度对轴承承载力的影响
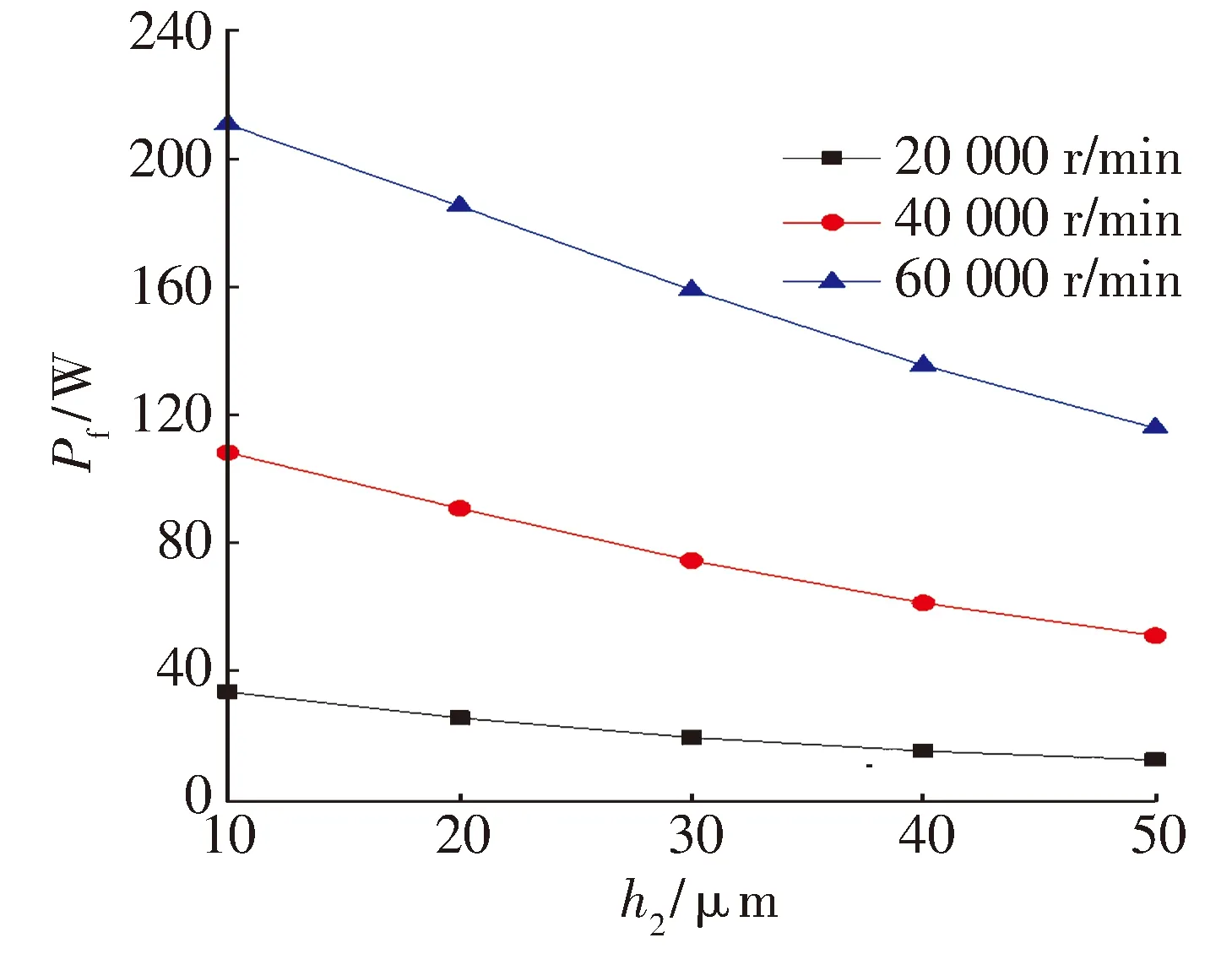
图16 不同转速下最小气膜厚度对摩擦功耗的影响
由图15可知,当最小气膜厚度增大时,轴承承载力呈减速下降的趋势,且各转速下的轴承承载力差值逐渐缩小;由图16可知,在不同转速下轴承的摩擦功耗均随最小气膜厚度的增大而减小,高转速的摩擦功耗明显高于低转速。轴承间隙的设计需在满足轴承承载力的前提下尽量减小摩擦功耗。
4 结论
通过求解修正雷诺方程,获得高压CO2在推力箔片轴承中的压力分布,求解轴承承载力和摩擦功耗,分析后得到以下结论:
1)在本文计算模型下,高压CO2与空气为润滑介质的轴承相比,高压会产生较大的箔片弹性变形;在相同转速下,高压CO2为润滑介质时的气膜厚度远大于空气的,且在不同转速条件下高压CO2的气膜厚度差异较大,而空气时差异较小;高压CO2为润滑介质的轴承承载力远大于空气的,空气在不同转速条件下的轴承承载力差异较小,而高压CO2差异较大。
2)瓦张角一定,节距比增大时,高压CO2为介质的轴承承载力呈先增大后减小的趋势;随着扇形瓦张角的增大,不同节距比的轴承最大承载力出现先增大后减小的趋势,不同的节距比,最佳瓦张角也不同;本文研究的推力箔片轴承,扇形瓦张角为45°、节距比为0.5时有较大的轴承承载力和较低的摩擦功耗。
3)当最小气膜厚度固定,存在一个最优楔形高度或最佳斜面倾斜角使轴承承载力最大,本文研究的推力箔片轴承最优楔形高度约为100 μm,此时倾斜角约为0.57°。
