基于DEM-FEM耦合的超声喷丸强化数值分析
2022-06-08蔡晋闫雪李威孟庆勋
蔡晋,闫雪,李威,孟庆勋
1. 沈阳航空航天大学 航空宇航学院,沈阳 110136 2. 中国航发上海商用航空发动机制造有限责任公司,上海 201306
超声喷丸强化是一种预应力表面强化工艺,通过弹丸冲击构件表面发生弹塑性变形引入残余压应力层,抑制裂纹扩展和延缓疲劳失效,提升叶片、盘、轴、鼓筒、轴颈等航空发动机、燃机轮机转子关键件的疲劳寿命。残余应力是消除外力和不均匀温度场等作用后仍留在构件内的自相平衡的内应力,对构件的影响包含两个方面:一方面是构件抗静、动载荷的变形能力,另一方面是载荷卸载后变形恢复的能力。表面强化后的表面形貌与残余应力状态影响构件的服役寿命,航空发动机零部件失效事件中,叶片引起的疲劳损坏和失效占70%左右,根本原因是材料缺陷以及残余压应力松弛,应力场分布不均匀,导致叶片榫头断裂引发灾难性事故,喷丸强化工艺参数的选择与强化效果影响相关。Murugaratnam等提出了离散单元理论,采用离散元方法(Discrete Element Method,DEM)模拟了喷丸强化过程,根据颗粒系统有限位移和旋转,分析弹丸与构件的相互作用进行离散颗粒轨迹,提出了DEM无法模拟喷丸处理后的构件表面塑性变形和残余应力仿真的问题,需结合有限元(Finite Element Method,FEM)分析构件表面的压应力。
针对超声喷丸强化工艺的接触/冲击问题,Nouguier-Lehon等采用Bucket Sort排序算法,在矩形腔室中模拟不同冲击速度下对圆柱杆件残余应力的影响,数值计算得到了平均冲击速度与平均冲击深度的关系。Rousseau等利用贝叶斯公式转换和抽样算法,结合Self-Kriging-Agent(自适应代理模型)的可靠性全局灵敏度,实现了喷丸零件覆盖率和残余应力的可视化。Badreddine等采用Event-Driven-Dynamics(事件驱动动力学)算法,追踪弹丸运动轨迹,计算粒子的加速度、速度和位置,提取了弹丸冲击速度和碰撞角度,研究表明,法向冲击(入射角小于10°)具有较高法向冲击速度(大于4 m/s),切向冲击(入射角大于60°)具有较低的冲击速度(小于1 m/s),弹丸数量越多,弹丸法向冲击次数越少。基于Event-Driven-Dynamics(事件驱动动力学)的算法,Badreddine等提出了一种CAD模型,研究腔室结构对弹丸冲击频率和冲击速度分布的影响,结果表明,在不同的腔室结构下,冲击频率是恒定的,冲击速度分布不同,高速冲击分布在中心区域,低速冲击分布在边缘部分,与传统喷丸相比,超声喷丸处理的构件具有较低的表面粗糙度和较好的表面质量。Micoulaut等基于拉格朗日框架下的Node-to-face算法,将离散相看作节点,有限单元作为主平面,通过罚函数法计算弹丸与弹丸、弹丸与零件之间的接触力,采用Newton-Raphson迭代搜索接触点和恢复系数,得到不同弹丸速度随零件、腔室壁及弹丸表面恢复系数的变化。Murugaratnam等采用刚体动力学(Rigid Body Dynamics)法模拟喷丸强化过程中弹丸与靶材的相互作用,在DEM代码中实现了动态调控弹丸对同一位置反复冲击产生的动态恢复系数,基于弹丸冲击路径的可视化分析,获取喷丸强化对构件表面应力分布的分析模型。Tu等采用Euler-Lagrange模型对离散相和耦合方程进行求解,通过迭代计算确定每个步长离散颗粒的作用力和位移,实现追踪每个弹丸的运动轨迹及能量场分布数据。
在超声喷丸DEM-FEM耦合理论模型的基础上,通过显式微粒离散中心差分法与拉格朗日-欧拉自适应网格(Arbitrary Lagrange Euler,ALE)算法,建立了高离散度超声喷丸过程的数值模型,分析超声喷丸DEM-FEM耦合过程中恒定恢复系数与动态恢复系数分别对表面残余应力、残余压应力层深度、表面宏观形貌的影响,对比模拟值与试验值,得出采用DEM-FEM耦合恒定恢复系数与动态恢复系数与试验值之间的偏差关系。
1 理论研究
1.1 超声喷丸弹-塑性DEM模型
超声喷丸过程中,弹丸对构件表面产生2种碰撞类型:弹性碰撞、塑性碰撞。采用显式微粒离散的中心差分法,通过Hertz-Mindlin(No Slip)接触定律,研究弹丸与构件之间的接触力为
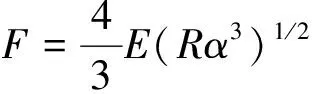
(1)
式中:为等效弹性模量;为弹丸等效半径;弹丸与构件碰撞时的变形量=+,为塑性变形量,为弹性变形量。如图1所示,为凹坑半径。
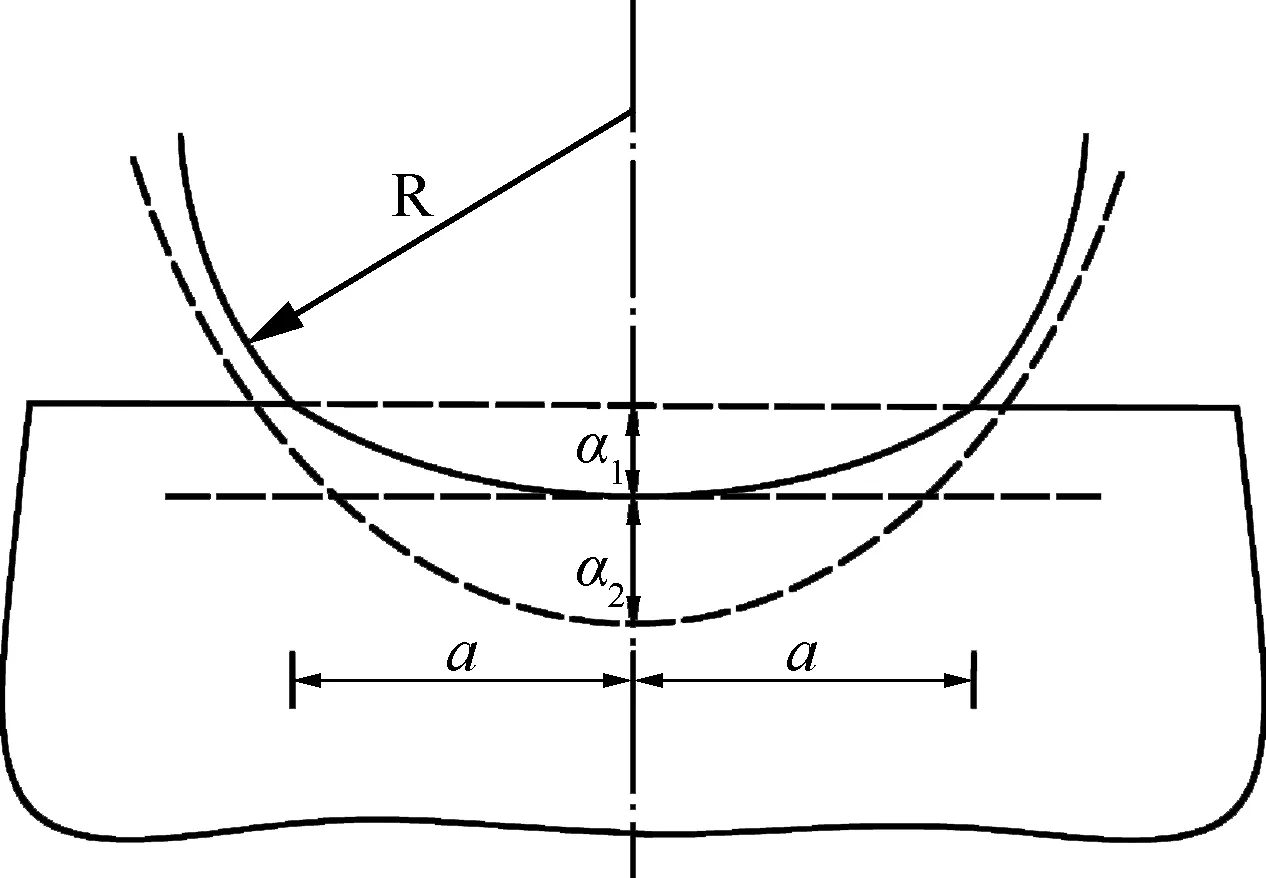
图1 弹丸与构件之间接触区域局部变形示意图Fig.1 Schematic diagram of local deformation of contact area between projectile and component
当弹丸与构件之间没有相对运动时,弹丸与构件碰撞时的变形量达到最大值,最大凹坑半径为
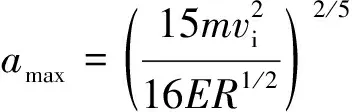
(2)
式中:为弹丸相对零件的相对冲击速度;为弹丸的质量。
根据式(1)和式(2),若在极限接触压力下,弹丸的屈服速度公式为
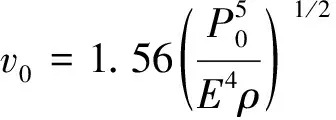
(3)
式中:相对速度为弹丸碰撞到零件时的屈服速度,弹丸冲击低于的相互作用为弹性碰撞;为弹丸的密度;极限接触压力为
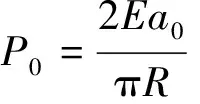
(4)
式中:为极限接触压力下的接触半径。
根据零件表面每次撞击的位置,可以在DEM代码中实现不同的恢复系数值随着时间变化在同一位置上撞击次数的函数。采用弹丸冲击速度与屈服速度的比值,可得恢复系数的表达式为
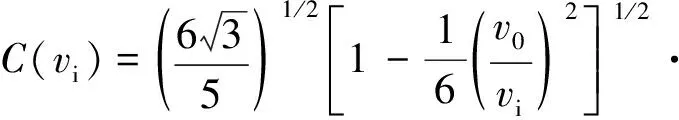

(5)
恢复系数是撞击前后相对法向速度之间的比率,属于冲击速度函数。采用速度函数的恢复系数可以降低非物理聚类趋势,通过阈值模型定义恢复系数的表达式为
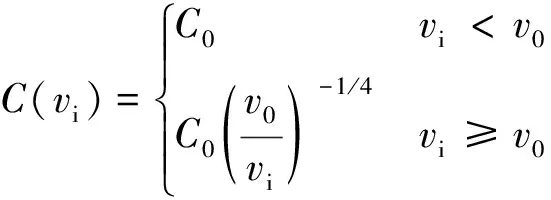
(6)
式中:为恒定法向恢复系数;当<时为弹性碰撞;当≥时为塑性碰撞。
1.2 超声喷丸DEM-FEM耦合模型
DEM无法模拟喷丸处理后表面的塑性变形和残余应力,需采用有限元来确定残余压应力和塑性变形。采用DEM-FEM耦合法分析弹丸与构件相互作用时,弹丸离散单元对构件的载荷作为矢量场的边界条件传递到有限元模型,可用来计算构件表面的应力场和位移场分布。因此需要确定构件在载荷作用下的等效节点载荷。根据虚功原理,等效节点应力表达式为
=
(7)
式中:为单元的等效节点力;为DEM的作用力;为单位形函数矩阵,采用三角形的面积坐标构造单元的形函数,即

(8)
式中:为三角形的面积坐标;为作用点与另外两个单元节点围成的面积;为三角形单元的面积,如图2所示。
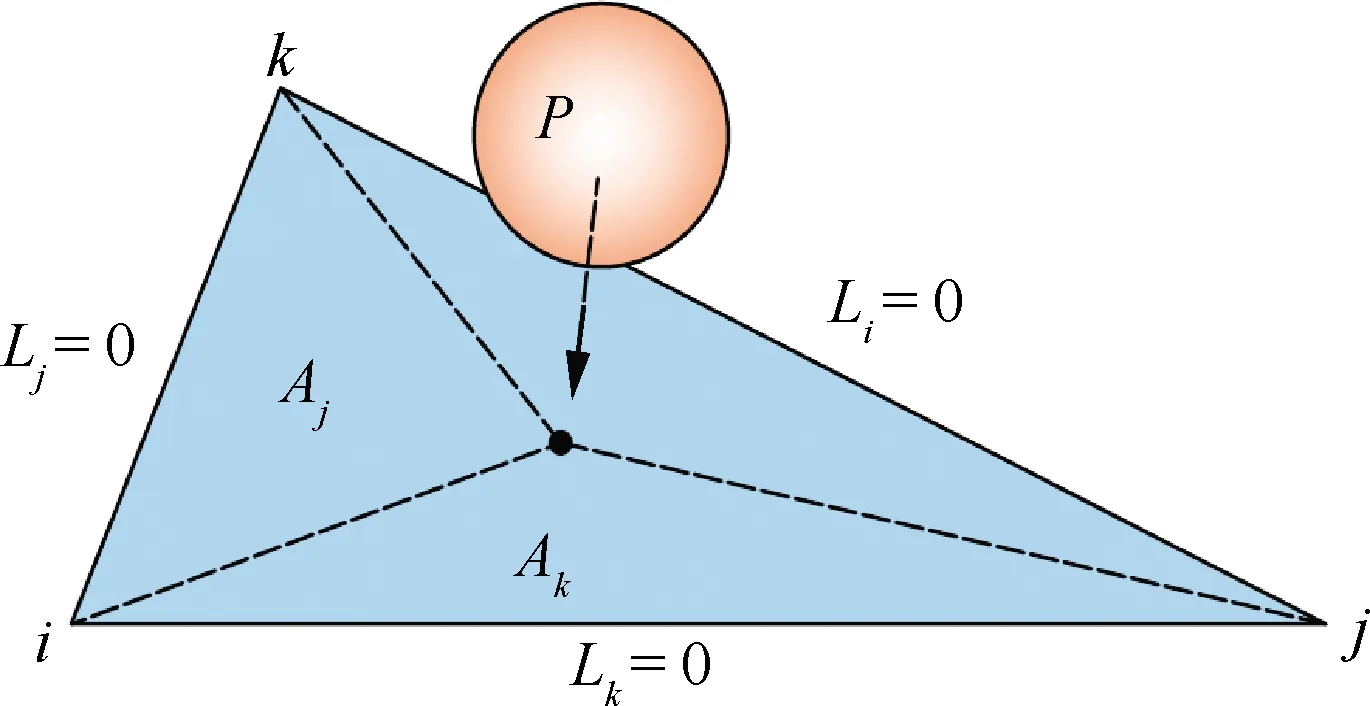
图2 等效节点应力计算模型Fig.2 Calculation model of equivalent element force
采用等效节点应力计算方程,将超声喷丸过程中产生的力转化为节点应力,计算单弹丸撞击作用下的应力场。超声喷丸过程中弹丸速度较高,因此需要在数值分析中考虑弹丸冲击速度对应力应变的影响。通过Johnson Cook材料本构模型,将应变速率引入模型中,热响应部分不予考虑,等效应力的公式为
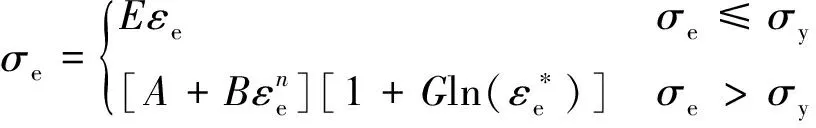
(9)
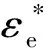
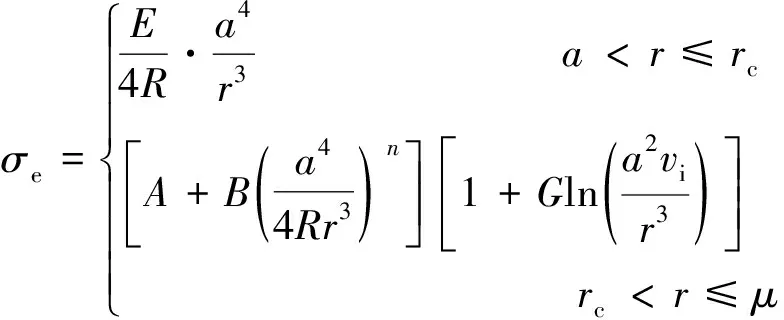
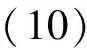
式中:为弹丸作用区半径;为塑性变形的界限半径;为弹性变形的界限半径。≤≤的区域,为塑性变形区;≤≤的区域,为弹性变形区,如图3所示。
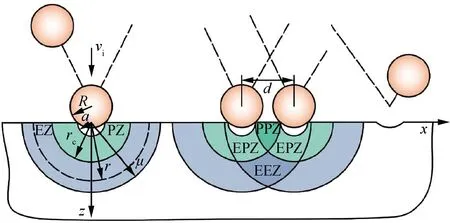
图3 相邻弹丸产生的应力场叠加示意图Fig.3 Schematic diagram of superposition of stress fields generated by adjacent projectiles
当=时,等效应力最大,即
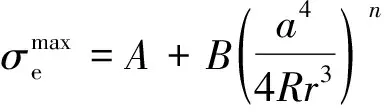
(11)
当=时,等效应力最小,即
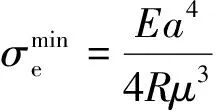
(12)
根据Avrami方程,多个弹丸冲击构件表面产生的应力场相互叠加,如图3所示,包含相邻弹丸叠加产生的塑性区(Plastic Zone,PZ)、弹性区(Elastic Zone,EZ)、塑性变形与塑性变形叠加区(Plastic and Plastic Superposition Zone,PPZ)、塑性变形与弹性变形叠加区(Elastic and Plastic Superposition Zone,EPZ)及弹性变形间的叠加区(Elastic and Elastic Superposition Zone,EEZ),弹塑性变形叠加区中的应力场在三维坐标系中可以表示为
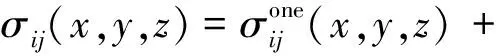
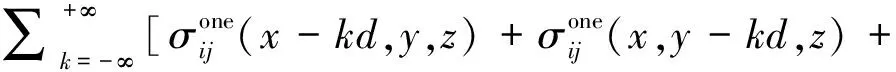

(13)

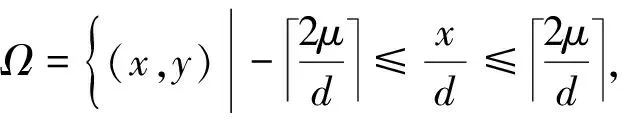
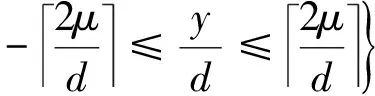
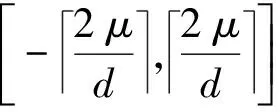
如图3所示,相邻间距为的弹丸以相同的初速度撞击构件表面,分别形成了以撞击点为中心的单弹丸及多弹丸撞击应力、塑性应变场。当相邻弹坑间距>2时,多个弹丸冲击构件表面产生的应力场没有产生叠加效应。当相邻弹坑间距≤2时,多个弹丸冲击产生应力场相互叠加效应。当≤2时,多个弹丸产生的塑性变形区和弹性变形区均可相互叠加。当>2时,多个弹丸产生的弹性变形区相互叠加,弹性变形范围增加,弹性变形区和塑性变形区相互叠加,但塑性变形区之间没有叠加。
在整个DEM-FEM计算中,超声喷丸强化过程属于动态接触/冲击。根据Hertz-Mindlin(No Slip)接触定律分析弹丸与构件之间的碰撞类型。通过显式微粒离散的中心差分法,采用Verlet方程在分析代码DDAD(不连续变形离散元分析)中进行耦合计算。在模拟瞬态或动态系统响应的数值模型中,计算出由于质点旋转而引起的应力增量。根据接触位置来建立ALE自适应网格,对接触力学矢量进行元素评估,记录弹丸对构件表面的冲击位置、冲击力、冲击次数和压痕的信息,从而应用等效应力检索残余应力值,弹丸与构件之间通过显式方法传递信息的过程如图4所示。
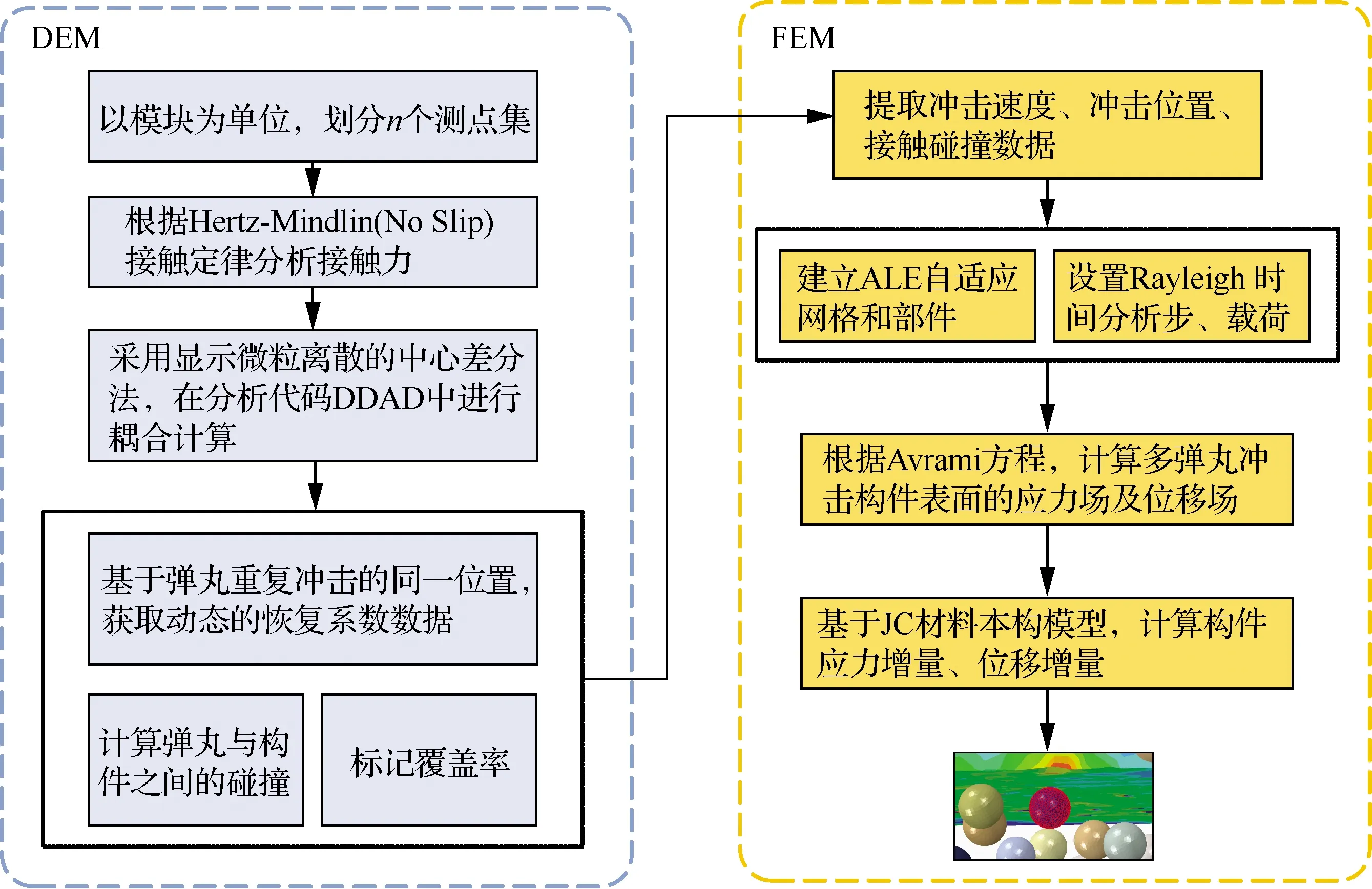
图4 超声喷丸数值计算分析框架流程[19]Fig.4 Analysis framework process of ultrasonic shot peening numerical calculation[19]
图5为超声喷丸DEM-FEM耦合分析过程示意图,使用DEM中的用户定义库(UDL),实现了一种针对同一位置的重复撞击改变恢复系数的算法,通过该算法可模拟超声喷丸冲击过程中不同对象之间的碰撞变形过程,相比刚性接触过程,能够更真实的反应对象间的真实碰撞及反弹过程,提高了后处理过程与试验值比较的精度范围,使模型预测更准确,通常弹丸与金属构件的恢复系数范围为0.5~0.9,DEM应用程序会为每次弹丸与构件的碰撞触发UDL模块,根据弹丸冲击次数和冲击力的叠加,在构件表面形成动态的恢复系数,检索出接触位置和接触力,将接触位置和接触力引入FEM模拟分析中,根据ALE自适应网格算法,在不改变原有网格的拓扑结构基础上,在单分析步的求解过程中逐步改善网格质量,修正网格局部畸变问题,为进一步研究弹丸与构件之间的变形规律奠定基础,包括:碰撞产生的等效应变场、应力场以及多弹丸对构件随机碰撞叠加的残余应力场。
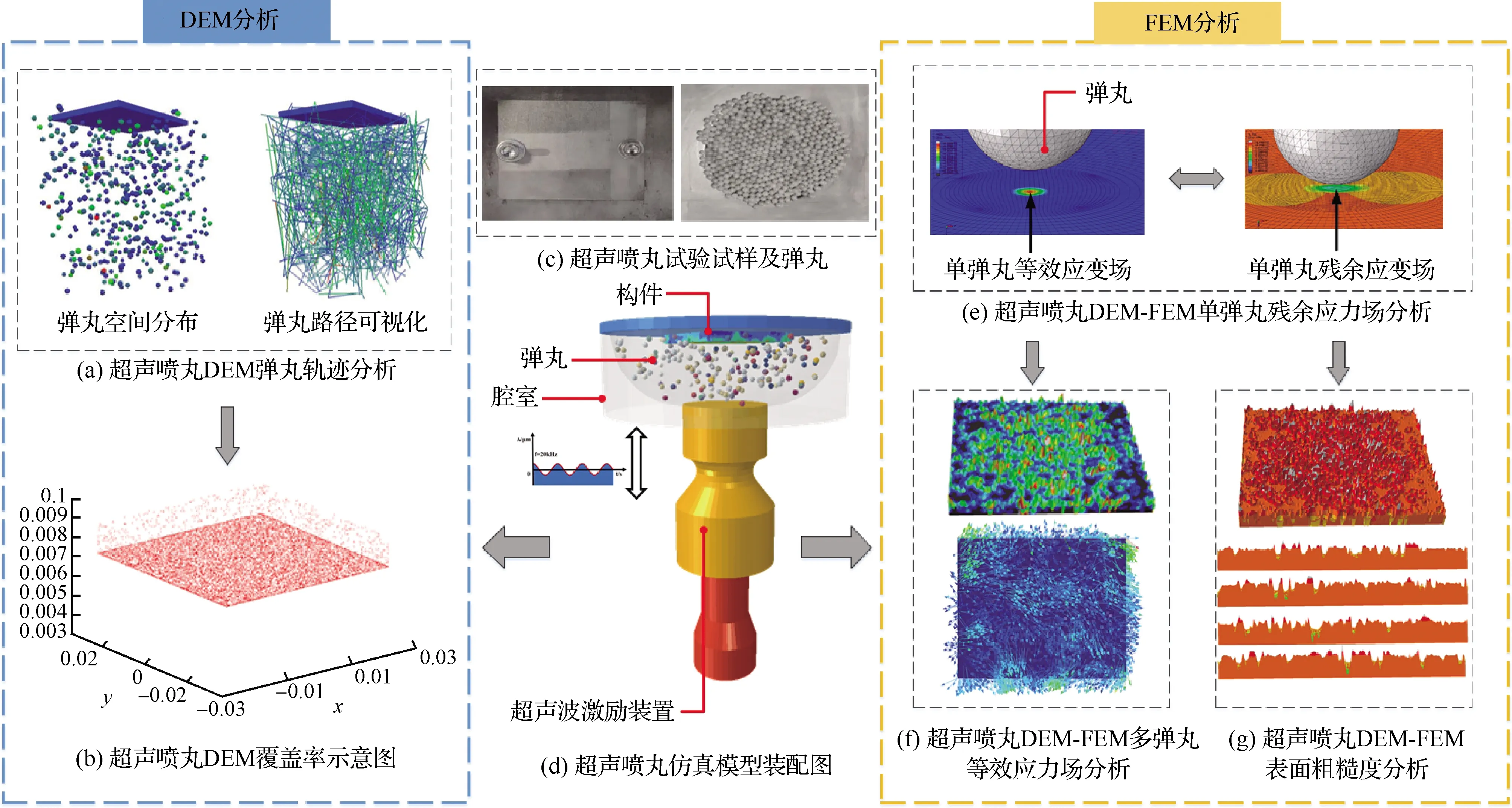
图5 超声喷丸DEM-FEM耦合分析过程示意图Fig.5 Schematic of coupling analysis of ultrasonic shot peening in DEM-FEM
2 仿真模型
2.1 本构模型参数的设定
研究对象为TC4钛合金材料,根据式(9)的本构模型,参数见表1。

表1 TC4材料本构模型参数Table 1 Material constitutive model parameters
2.2 模型尺寸及边界条件
试验与数值模拟过程中试样尺寸均为50 mm×60 mm×5 mm,仿真过程中TC4钛合金试样与振动系统材料密度为4.4 g/cm,弹性模量为110 000 MPa,屈服强度919 MPa,泊松比0.3,弹丸密度为6 g/cm,弹性模量为208 000 MPa,腔室密度为7.81 g/cm,弹性模量为210 000 MPa,泊松比0.3,TC4钛合金试样、超声喷丸腔室采用完全固定的约束方式,弹丸采用刚体约束方式,具体材料属性如表2所示。
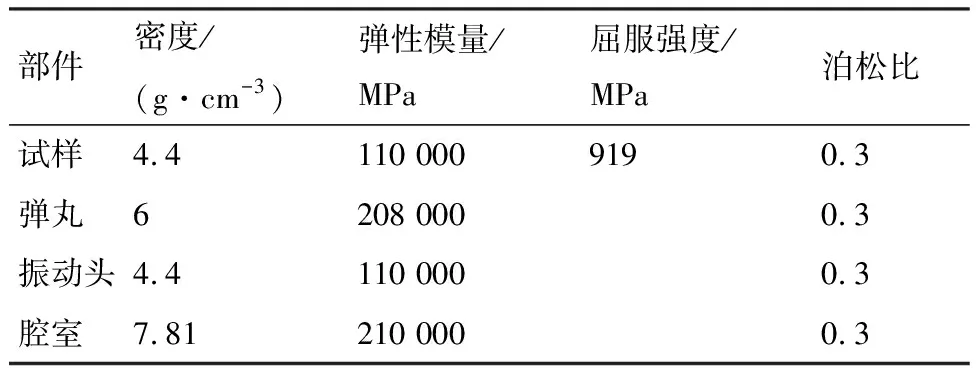
表2 各部件材料属性Table 2 Material properties of each component
3 试验材料及研究方法
对TC4钛合金表面精磨处理,降低表面处理时热应力对试样表面应力场造成影响,依据超声喷丸标准AMS2580A,采用0.1~0.15 A喷丸强度对试样进行超声喷丸处理,超声喷丸工艺参数如表3所示,采用ZrO弹丸材料,弹丸直径为2.5 mm,弹丸数量500个,振动头振幅设置40 μm,覆盖率不小于98%。
经过超声喷丸处理后,采用超景深三维可视化(VHX-900)轮廓仪对喷丸表面进行形貌表征,采用Proto LXRD型X射线应力仪检测试样残余应力分布,衍射时采用CuKα靶材,通过电解抛光剥层技术测定残余应力沿试样深度的分布,由于剥层前后,沿试样深度分布应力差异较小,本文采用剥层后的直接测量值。

表3 TC4合金超声喷丸工艺参数Table 3 Ultrasonic shot peening process parameters of TC4 alloy
4 DEM-FEM耦合恢复系数对残余应力场的影响
4.1 表面残余应力场
图6为不同恢复系数TC4钛合金超声喷丸表面残余应力场,以相同距离建立5条应力检测路径(图6中红色箭头),统计不同恢复系数下,每条路径应力场均值及总体均值的差异变化(后文残余应力层深度、表面宏观形貌的分布规律分析,均采用该多路径统计方式),在DEM-FEM耦合数值模型中分别设置恢复系数为0.5、0.7、0.9以及动态恢复系数类型,4种恢复系数类型状态下,表面残余应力基本处于压应力状态,残余压应力范围约为(0~-620 MPa),与杨天南等在TC4钛合金超声喷丸表面状态研究中60 μm振幅下常规应力阶段吻合,在试样边缘小区域范围内由于产生应力集中效应,存在部分残余拉应力,残余拉应力范围约为(0~350 MPa),高于实际超声喷丸试验过程中试样边缘的拉应力分布范围,图6中表面残余应力场显示,恢复系数由0.5增加至0.9的过程中,表面残余压应力场分布显著增加,采用动态恢复系数后,表面残余压应力均值状态处于恢复系数0.7与0.9表面残余压应力均值状态之间。
图7统计了每个模型中试块表面相同位置路径1~路径5的残余压应力分布,统计结果显示,恢复系数由0.5~0.9的过程中,极值差降低14 MPa,下降约38%,表明试块表明应力场逐渐趋于均匀,由0.9至动态恢复系数的过程中,极值差增加3 MPa,差异较小。

图6 不同恢复系数TC4钛合金超声喷丸表面残余应力场Fig.6 Surface residual stress field of TC4 titanium alloy with different recovery coefficients by ultrasonic shot peening
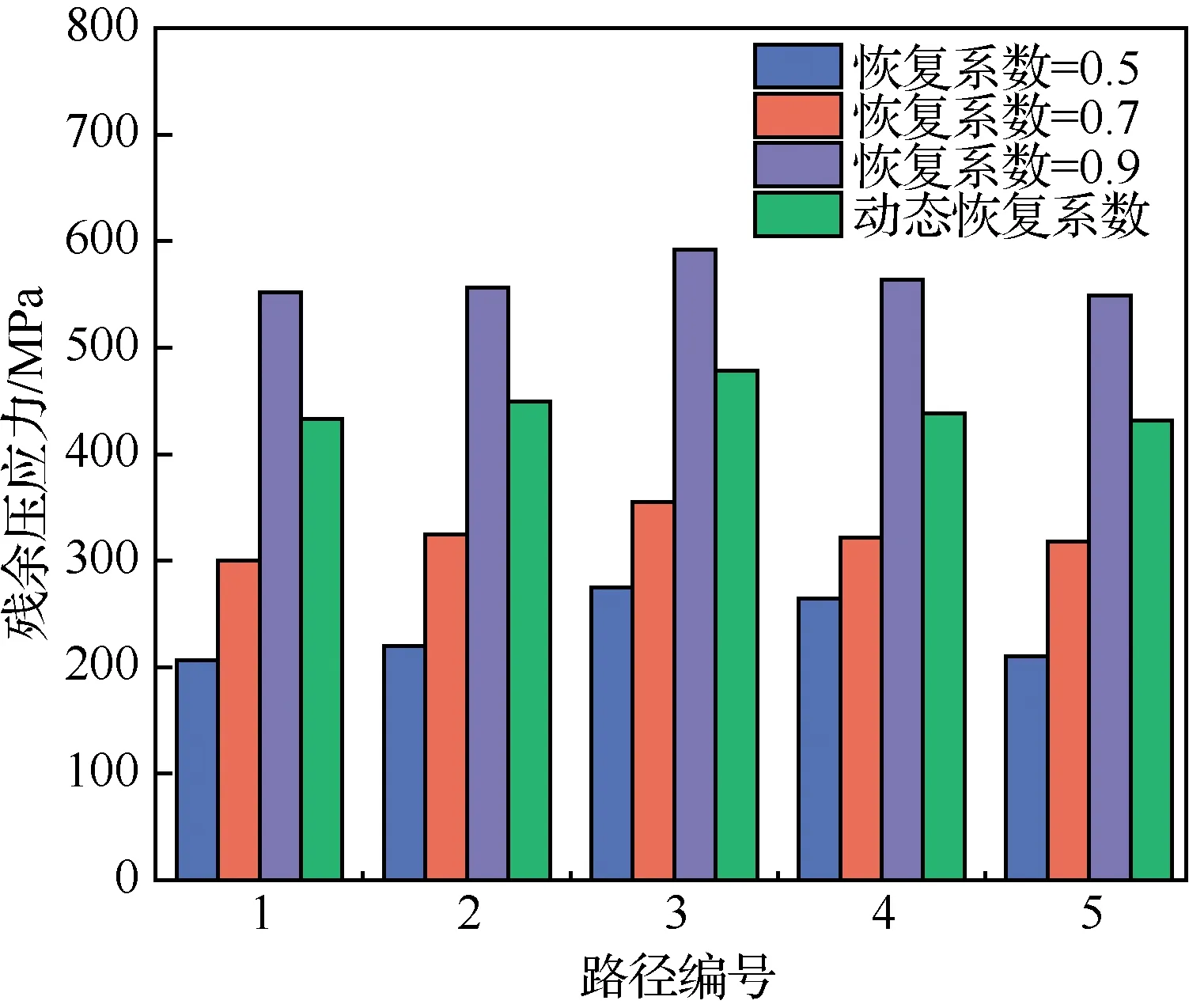
图7 TC4钛合金超声喷丸表面残余应力统计Fig.7 Statistics of residual stress on the surface of TC4 titanium alloy by ultrasonic shot peening
恢复系数由0.5~0.9的过程中,试样两端与中间部分应力均值差降低26 MPa,由0.9至动态恢复系数的过程中,应力均值差增加3 MPa,差异较小,与极值差趋势相近。
图8统计了4种恢复系数下TC4钛合金超声喷丸表面残余压应力均值差异,恢复系数由0.5至动态恢复系数的过程中,检测路径均值总体呈增加的趋势,其中恢复系数由0.5~0.9的过程中,5条检测路径残余应力均值增加328 MPa,约提高140%,相比恢复系数0.9,动态恢复系数5条检测路径残余应力均值由563 MPa下降至446 MPa,约降低21%,相比恢复系数0.7,动态恢复系数5条检测路径残余应力均值由324 MPa增加至446 MPa,约提高38%。结果表明,在该组超声喷丸工艺参数下,采用动态恢复系数表面残余压应力整体均值、极值差以及两端与中心平均差值处于0.7~0.9恢复系数残余应力均值范围间。

图8 TC4钛合金超声喷丸表面平均残余应力统计Fig.8 Statistics of average residual stress on the surface of TC4 titanium alloy by ultrasonic shot peening
4.2 截面残余应力场
图9为不同恢复系数TC4钛合金超声喷丸沿残余应力检测路径的截面残余应力场,4种状态下,仅试样表层区域处于压应力状态,其他部分亚表面区域为补偿拉应力状态,取表面至近表层0.6 mm深度进行应力场分析,图9中截面残余应力场显示,由恢复系数0.5~0.9的过程中,截面残余压应力层深度及沿深度压应力值呈增加的趋势,恢复系数0.9与动态恢复系数截面残余压应力层深度及值相近。
图10统计了不同恢复系数下,每个模型中试块截面相同位置范围内路径1~路径5的残余压应力层深度,统计结果显示,恢复系数由0.5~0.9的过程中,极值差降低0.03 mm,下降约50%,由0.9至动态恢复系数的过程中,极值差由0.03 mm降低至0.02 mm,极值差降低0.01 mm,降低约33%。

图9 不同恢复系数TC4钛合金超声喷丸残余压应力层深度Fig.9 Depth of compressive residual stress in ultrasonic shot peening of TC4 titanium alloy with different recovery coefficients

图10 TC4钛合金超声喷丸残余压应力层深度统计Fig.10 Statistics of residual stress on surface of TC4 titanium alloy by ultrasonic shot peening
在每种恢复系数下,路径1与路径5(即处于两端的检测路径)残余压应力层深度均值均低于路径2~路径4(即处于中间的检测路径),恢复系数为0.5时,两端平均残余压应力层深度均值为0.15 mm,中心3条检测残余压应力层深度均值为0.18 mm,两端较中心3条检测路径残余压应力深度均值约降低0.03 mm。恢复系数为0.7时,两端平均残余压应力深度均值为0.17 mm,中心3条检测残余应力均值为0.2 mm,两端较中心3条检测路径残余压应力均值约降低0.03 mm。恢复系数为0.9时,两端平均残余压应力深度均值为0.25 mm,中心3条检测残余压应力深度均值为0.26 mm,两端较中心3条检测路径残余压应力深度均值约降低0.01 mm。采用动态恢复系数时,两端平均残余压应力深度均值为0.23 mm,中心3条检测残余压应力深度均值为0.233 mm,两端较中心3条检测路径残余压应力深度均值约降低0.003 mm。恢复系数由0.5~0.9的过程中,残余压应力深度均值差由0.03 mm降低至0.01 mm,残余压应力深度均值差降低0.02 mm,约下降67%,由0.9至动态恢复系数的过程中,残余压应力深度均值差降低0.007 mm,差异较小,与极值差趋势相近。
图11统计了4种恢复系数下TC4钛合金超声喷丸残余压应力层深度均值差异,恢复系数由0.5至动态恢复系数的过程中,检测路径残余压应力深度均值总体呈增加的趋势。其中恢复系数由0.5~0.9的过程中,5条检测路径残余压应力深度均值由0.17 mm增加至0.25 mm,增加0.08 mm,约提高47%,相比恢复系数0.9,动态恢复系数5条检测路径残余压应力深度均值由0.25 mm下降至0.23 mm,降低约0.02 mm,约降低8%;相比恢复系数0.7,动态恢复系数5条检测路径残余压应力层深度均值由0.19 mm增加至0.23 mm,增加约0.04 mm,约提高21%。结果表明,在该组超声喷丸工艺参数下,采用动态恢复系数残余压应力深度整体均值、极值差以及两端与中心平均差值处于0.7~0.9恢复系数残余压应力深度均值范围间。
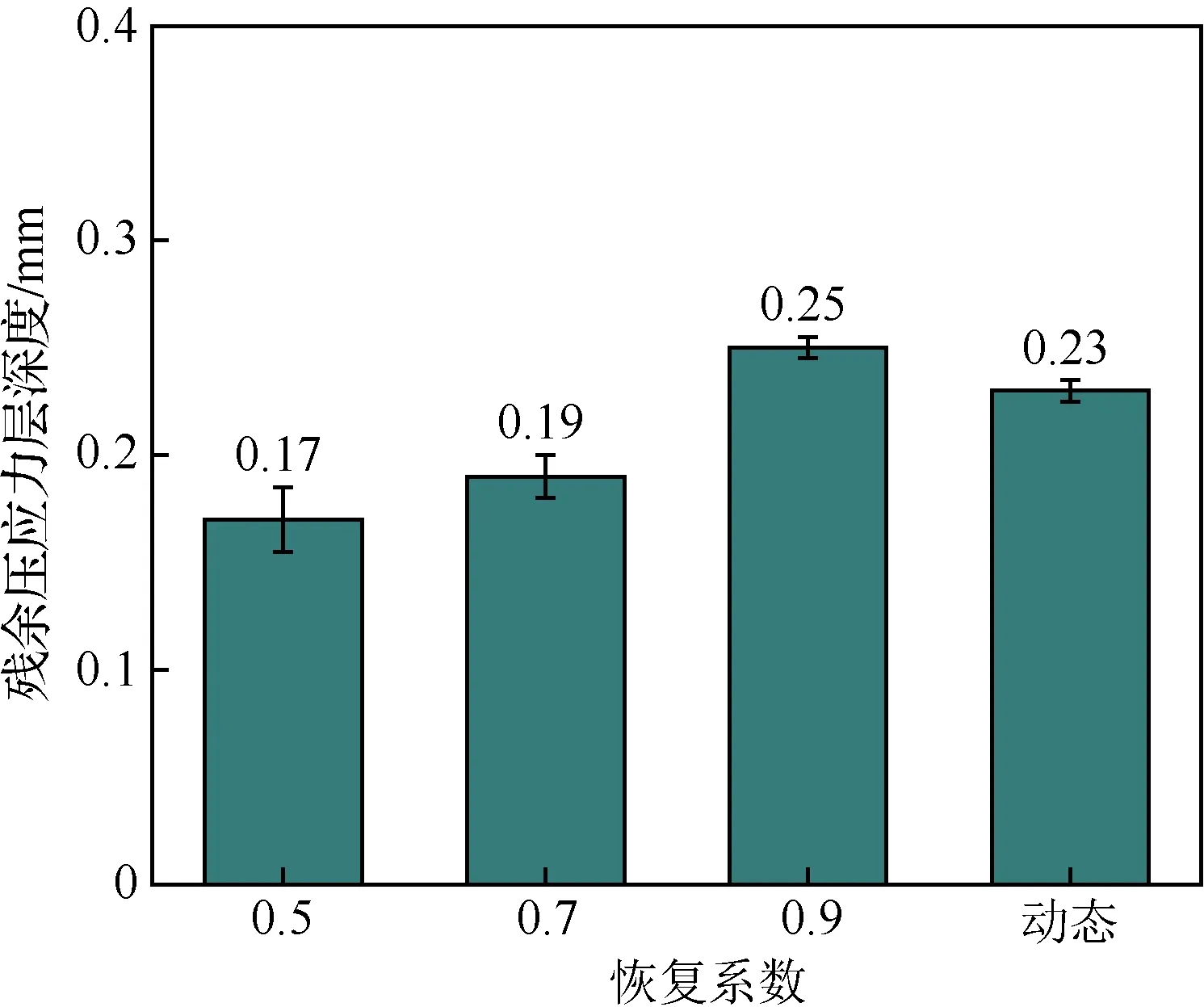
图11 TC4钛合金超声喷丸平均残余压应力层深度统计Fig.11 Statistics of average residual stress on surface of TC4 titanium alloy by ultrasonic shot peening
4.3 表面宏观形貌
图12对4种恢复系数类型试块进行了剖面粗糙度检测,通过几何形貌透视化分析多弹丸冲击TC4钛合金试样表面后的凸起及凹坑区域的几何分布特征,对弹丸冲击导致的凹坑及凸起区域进行轮廓标识,整体表面冲击形貌基本处于相近的变形区间,恢复系数的增加的过程中,剖面凸起程度显著增加,边缘区域受残余拉应力影响,凸起及凹陷特征显著,试样中部区域与振动头垂直距离较短,凸起及凹陷程度较中部与边缘之间的区域变形程度明显,动态恢复系数状态下,剖面凸起程度处于恢复系数0.7~0.9状态之间。

图12 不同恢复系数TC4钛合金超声喷丸粗糙度检测Fig.12 Surface roughness testing of TC4 titanium alloy with different recovery coefficients by ultrasonic shot peening

图13 不同恢复系数TC4钛合金超声喷丸表面宏观形貌Fig.13 Surface macro morphology of TC4 titanium alloy with different recovery coefficients by ultrasonic shot peening
图13为4种恢复系数超声喷丸表面宏观形貌,对表面形貌沿纵向放大100倍,恢复系数设置由0.5至动态恢复系数的过程中,试样表面塑性变形程度随恢复系数的增加变化显著,超声喷丸表面凸起与凹陷特征趋于明显。
图14统计结果显示,在每种恢复系数下,路径1与路径5表面轮廓平均算数偏差均值均低于路径2~路径4,恢复系数由0.5~0.9的过程中,表面轮廓平均算数偏差均值差降低0.13 μm,约下降52%,由0.9至动态恢复系数的过程中,表面轮廓平均算数偏差均值差由0.12 μm减少至0.07 μm,降低0.05 μm,差异较小,与极值差趋势相近。
图15统计了4种恢复系数下TC4钛合金超声喷丸表面轮廓平均算数偏差均值差异,恢复系数由0.5至动态恢复系数的过程中,表面轮廓平均算数偏差均值总体呈增加的趋势。其中恢复系数由0.5~0.9的过程中,5条路径粗糙度均值由0.9 μm增加至2.1 μm,增加1.2 μm,约提高133%,相比恢复系数0.9,动态恢复系数5条路径残余应力均值由2.1 μm下降至1.8 μm,减少0.3 μm,约降低14%;相比恢复系数0.7,动态恢复系数5条路径粗糙度均值由1.4 μm增加至1.8 μm,增加0.4 μm,约提高38%。结果表明,在该组超声喷丸工艺参数下,采用动态恢复系数粗糙度整体均值、极值差以及两端与中心平均差值处于0.7~0.9恢复系数粗糙度均值范围间。
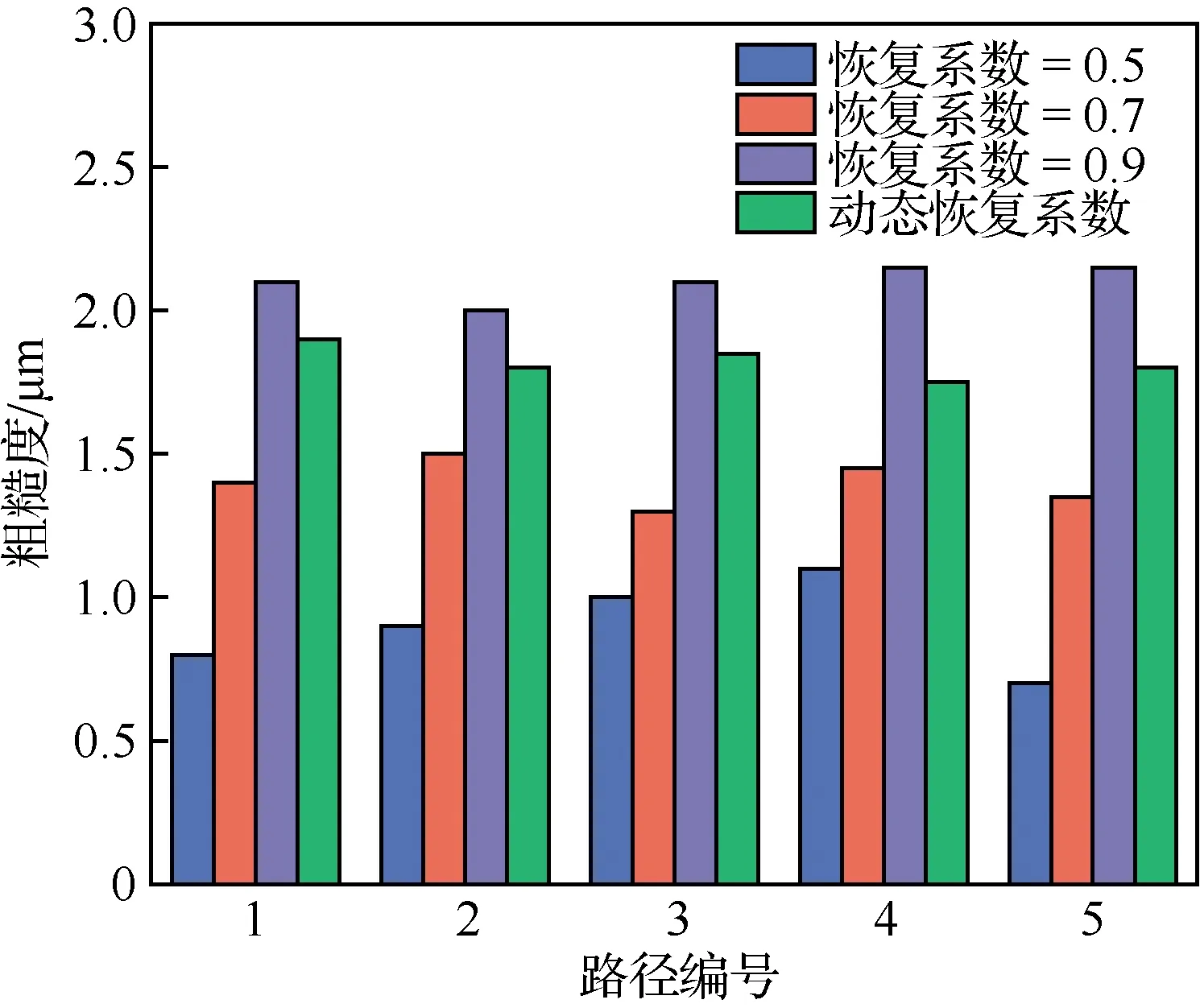
图14 试样表面粗糙度统计Fig.14 Statistics of roughness on the surface of the sample
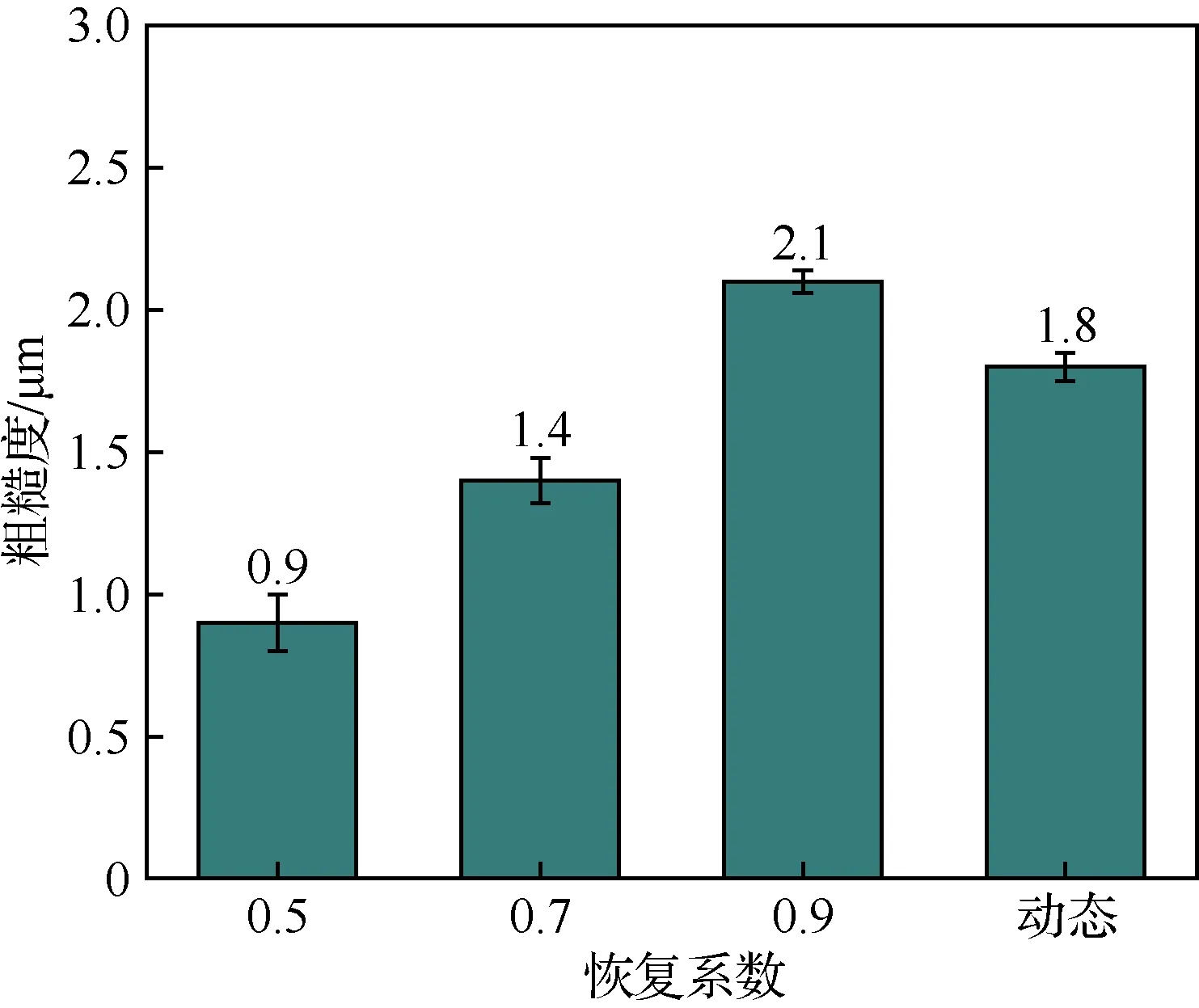
图15 TC4钛合金超声喷丸平均粗糙度统计Fig.15 Statistics of average residual stress on the surface of TC4 titanium alloy by ultrasonic shot peening
5 超声喷丸试验结果分析
图16为相同工艺参数情况下,TC4钛合金超声喷丸试块试验表面粗糙度检测宏观形貌结果,与表面形貌仿真透视化分布特征相似,凹坑分布密度较相似,表面宏观变形范围基本均匀。图17对比了DEM-FEM耦合模型在4种恢复系数下与超声喷丸试验表面轮廓平均算数偏差粗糙度均值,结果显示,试验检测表面粗糙度为1.9 μm,与恢复系数0.9模型相比,减少0.2 μm,下降约10%,与采用动态恢复系数相比,增加0.1 μm,提高约5%。
图18、图19比较了TC4钛合金超声喷丸试块表面及截面残余应力试验值与4种恢复系数的仿真结果,结果显示,超声喷丸试验试块表面残余压应力均值为461 MPa,与恢复系数0.9模型相比,减少114 MPa,下降约20%,与采用动态恢复系数相比,增加7 MPa,提高约1.5%。超声喷丸试验试块表面残余压应力层深度均值为0.22 mm,与恢复系数0.9模型相比,减少0.03 mm,下降约12%,与采用动态恢复系数相比,减少0.01 mm,下降约4.3%。
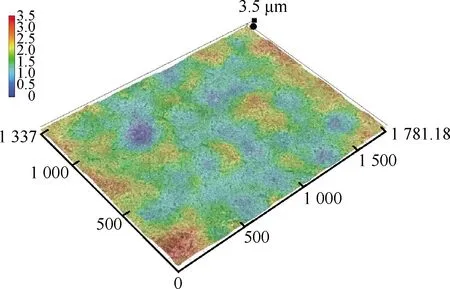
图16 TC4钛合金超声喷丸表面粗糙度检测Fig.16 Surface roughness testing of TC4 titanium alloy by ultrasonic shot peening
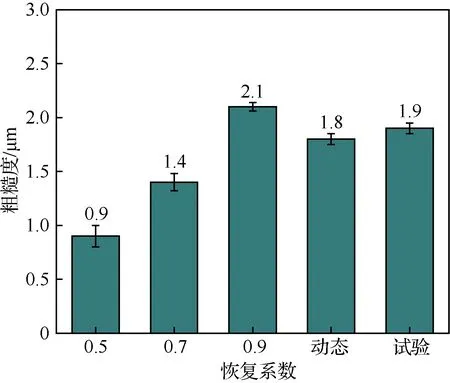
图17 超声喷丸粗糙度试验值与仿真值比较Fig.17 Comparison of experimental value and simulation value of ultrasonic shot peening roughness
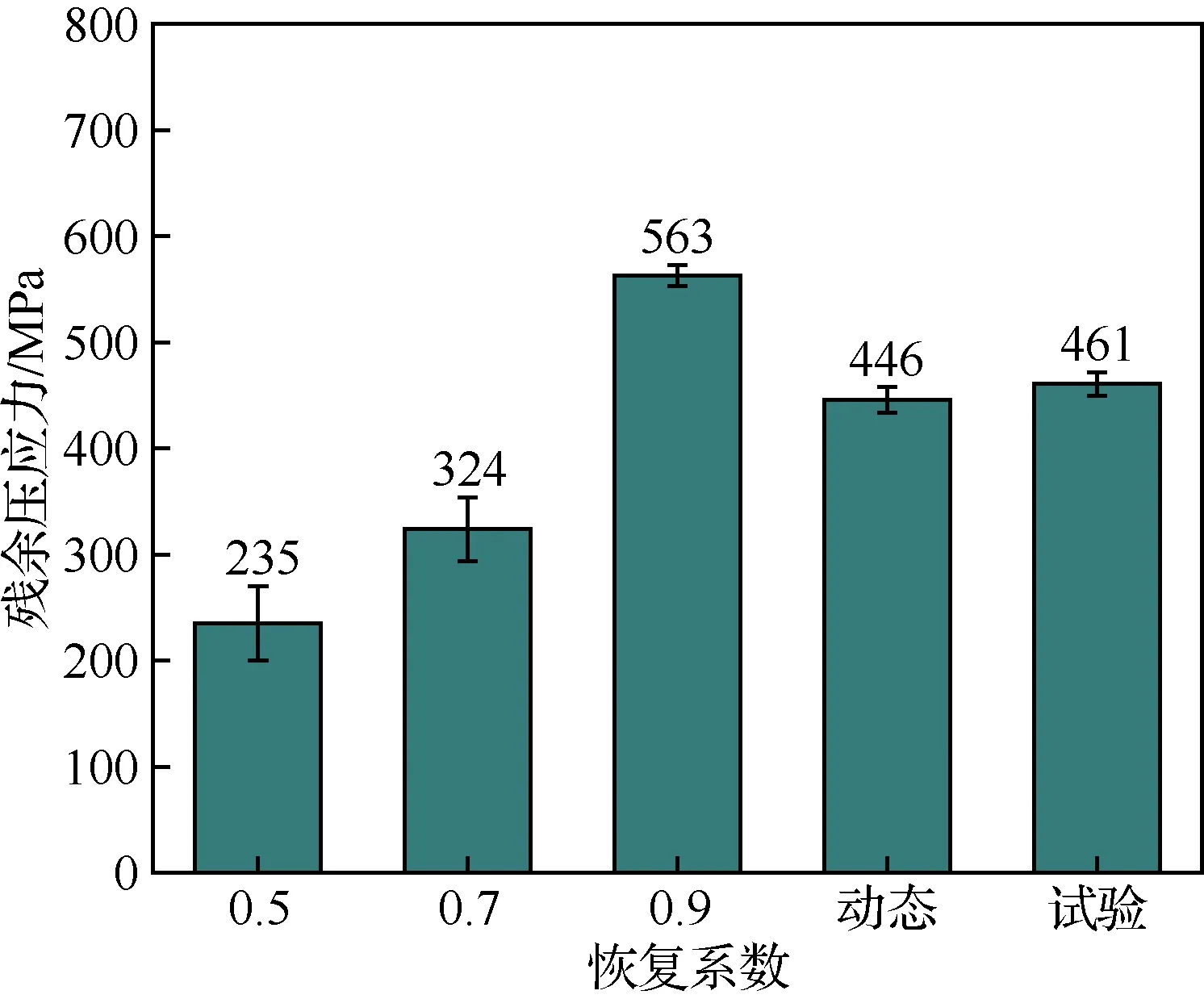
图18 超声喷丸表面残余应力试验值与仿真值Fig.18 Experimental value and simulation value of ultrasonic shot peening surface residual stress
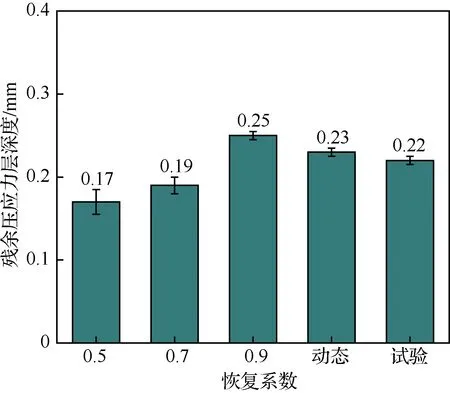
图19 超声喷丸残余应力深度试验值与仿真值Fig.19 Experimental value and simulation value of residual stress thickness by ultrasonic shot peening
4种恢复系数结果表明,与超声喷丸工艺试验及理化检测结果相比,DEM-FEM仿真结果差异较小,相比恒定值恢复系数,在表面残余压应力均值、残余压应力层深度及表面粗糙度方面,采用动态恢复系数更接近试验值,预测更准确。
6 结 论
1) 采用显式微粒离散函数的多弹丸撞击模型,可以获得弹丸冲击速度与恢复系数的关系,解决恢复系数动态变化引起的残余应力的求解问题。
2) 由恢复系数0.5~0.9的过程中,表面残余压应力、残余压应力层深度、表面粗糙度均增加,相比残余应力层深度与表面粗糙度,表面残余应力分布极值差低约12%,更易实现均匀分布。
3) 在每种恢复系数下,由于振动头与试块的位置关系,处于两端的检测路径表面残余压应力、残余压应力层深度、表面粗糙度均低于处于中间的检测路径。相比残余应力层深度内外端均值差值,表面残余应力与表面粗糙度差值低约9%~15%,分布更均匀。
4) 相比恒定值恢复系数,在表面残余压应力、残余压应力层深度及表面粗糙度方面,采用动态恢复系数与试验值误差均低于5%,预测更接近真实值,通过DEM-FEM工艺仿真可以实现简单试块应力场及形貌状态的有效预测,为进一步开展复杂结构零件超声喷丸研究提供思路。
