离散无向图模型维数的计算
2022-06-07张春妮李本崇
刘 芸, 张春妮, 李本崇
(西安电子科技大学 数学与统计学院, 陕西 西安 710126)
一个图模型是一族概率分布,这里图用来表示随机变量间的条件独立关系。图中顶点表示随机变量,图中的条件独立情形由与之相关的分离准则确定。无向图模型已在统计学和机器学习的许多问题中得到应用[1-3]。
在无向图模型中,模型的维数问题对于检验[1]和模型选择[2]来说都非常重要。文献[1]中命题4.35给出了离散可分解图模型维数的显式计算公式。此外,还给出了一个计算层次模型维数的递归公式,层次模型的一个特殊类型是离散无向图模型(DUGMs)。文献[4]将参数定义的模型转化为隐式描述,并从代数几何的角度分析了DUGMs。事实上,这种代数几何刻画的思想起源于文献[5]。给定一个DUGM,可以将其对应的环面理想的维数看作该模型的维数,但并没有明确的公式可用来计算相应的环面理想的维数或相关矩阵的秩。文献[6]提出了一种新的链图参数化方法,将链图模型的维数定义为参数化过程中可自由设定的参数个数,即文献[6]给出了一个显式的计算DUGMs的维数公式。本文研究DUGMs维数的两个定义是否一致。
一个概念类的Vapnik-Chervonenkis维数和欧氏嵌入空间的最小维数是评价一个分类器分类性能的两个重要指标[7-8]。文献[9]证明了任意k值离散可分解图模型诱导出的概念类的Vapnik-Chervonenkis维数和欧氏嵌入空间的最小维数等于其独立参数的个数加1。文献[10]证明了对于任意给定的DUGM,其诱导的概念类的Vapnik-Chervonenkis维数和欧氏嵌入空间的最小维数相同。这些工作也启发我们去讨论DUGMs维数的两个定义之间的关系。
本文探究了上述DUGMs维数的2个定义之间的关系,证明了对任意的DUGM,这两种定义下维数的差值为1,即两个定义等价。因此,文献[1]中的命题4.35可推广到一般的DUGMs。
1 定义和符号
本节给出一些定义及其性质。本文中,N={X1,X2,…,Xn}表示非空的有限随机变量集,并假设每个离散变量Xi的取值为[ri]={1,2,…,ri},其中ri≥2,是一个正整数。
1.1 无向图
本文考虑简单无向图,有关图论更多的介绍,可参考文献[4]。无向图可表示为G=(N,E),其中N为所有顶点的集合,E为边的集合。若G中两个顶点X、Y的无序对(X,Y)∈E,则称这两个顶点相邻。如果顶点集K⊆N,且K中任意不相同的顶点的无序对均在E中,即∀X,Y∈K,X≠Y,(X,Y)∈E,则称顶点集K是完全的。特别地,空集∅也是完全的。无向图G的所有非空完全集构成的集合记作C(G)。G中的最大完全集称为团,所有团的集合记作KG。
路是一个顶点序列X=Y1,Y2,…,Yk=Y,k≥2,其中(Yi,Yi+1)∈E,i=1,2,…,k-1。∀N1,N2⊆N,N1∩N2=∅,N3⊆N(N1∪N2),若无向图G中X∈N1和Y∈N2之间的每条路都至少包含N3中的一个点,那么我们就说N3分离了N1和N2。对于集合S⊆N,G(S)表示以S为顶点集的G的导出子图。给定一个无向图G,如果不交三元组(N1,N2,N3)满足:(ⅰ)N=N1∪N2∪N3;(ⅱ)N3分离N1和N2;(ⅲ)N3是N的完全子集,则称该三元组构成G的一个分解。即(N1,N2,N3)将G分解为两个子图G(N1∪N3)和G(N2∪N3),且G(N1∪N3)⊕G(N2∪N3)是直和。若子集N1,N2⊆N都非空,则这是一个真分解。若G存在一个真分解,则该无向图是可约的,否则是素的。
下面通过一个例子说明部分概念。
例1如图1所示无向图G1。
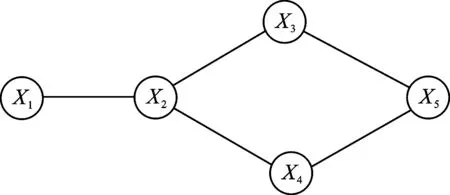
图1 无向图G1
C(G1)={{X1},{X2},{X3},{X4},{X5},
{X1,X2},{X2,X3},{X2,X4},
{X3,X5},{X4,X5}}。
KG1中的元素为{X1,X2},{X2,X3},{X2,X4},{X3,X5},{X4,X5}。
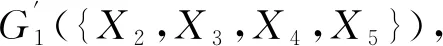
1.2 离散无向图模型
给定一个无向图G,与之相关联的图模型为一族分布,每一个分布P可分解为如下形式:
(1)
式中:x∈χ=[r1]×[r2]×…×[rn];ψC(·)的取值仅依赖x中与团C中变量对应的值。文献[4]将相应的图模型视为单项式映射φA(G)的像集,映射如下:
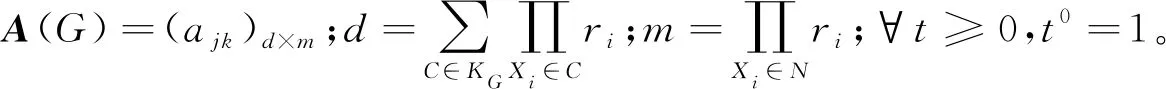
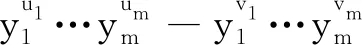
文献[6]提出了一种将链图参数化的新方法。特别地,于无向图而言,有

例2(续例1) 对于图1中的无向图G1,若对i=1,2,3,4,5,均有ri=2。5个团对应的函数共有d=20个取值,分别为
t1=ψ1,2(11),t2=ψ1,2(12),t3=ψ1,2(21),
t4=ψ1,2(22),t5=ψ2,3(11),t6=ψ2,3(12),
t7=ψ2,3(21),t8=ψ2,3(22),t9=ψ2,4(11),
t10=ψ2,4(12),t11=ψ2,4(21),
t12=ψ2,4(22),t13=ψ3,5(11),
t14=ψ3,5(12),t15=ψ3,5(21),
t16=ψ3,5(22),t17=ψ4,5(11),
t18=ψ4,5(12),t19=ψ4,5(21),
t20=ψ4,5(22),
式中ψi,k(xixk)是ψ{Xi,Xk}(xi,xk)的简写。
由定义知本例中可自由设定的参数为ψ1(2)、ψ2(2)、ψ3(2)、ψ4(2)、ψ5(2)、ψ1,2(22)、ψ2,3(22)、ψ2,4(22)、ψ3,5(22)、ψ4,5(22),因此d′=10。
1.3 层次模型的维数
超图是有限集N的幂集的一个子集,记作H,里面的元素称为超边。例如,无向图G的KG是一个超图。若超图H中没有任何一个超边是其他超边的子集,则该超图是约化的。约化超图可以看作层次模型的生成类。通过移除超图H中所有包含在其他超边中的超边,运算red H便可产生H的约化超图。关于2个超边的交运算和并运算如下:
A∨B=red(A∪B),
A∧B=red(A∩B|A∈A,B∈B)。
定义在χ上的实值函数形成向量空间L,其中L为欧几里得空间,可在其上定义内积
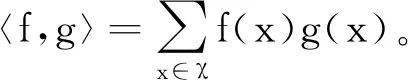
对于N的子集A,L的因子子空间FA是通过xA依赖于x的函数集,即对所有令xA=yA的x,y,
f∈FA⟺f(x)=f(y)。
层次模型由含有如下形式的层次模型子空间确定:
文献[1]给出了计算层次模型(层次模型子空间)维数的计算公式
dimHA∨B=dimHA+dimHB-dimHA∧B,
无向图G的离散无向图模型就是一个层次模型,其生成类为κG。
2 离散无向图模型的维数
本节将证明离散无向图模型维数的2种定义本质上一致。
首先,考虑完全无向图对应的离散无向图模型。
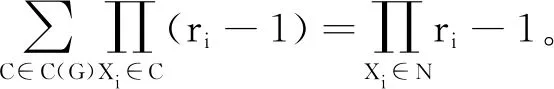
证明通过对|N|用归纳法来进行证明。当|N|=1时,等式显然成立。假设该引理适用于所有顶点数不少于k的完全图,当|N|=k+1时,则有
还注意到如下引理。
引理2给定一个无向图G,若N3分离N1和N2,则有如下等式成立:
C(G)=C(G(N1∪N3))∪C(G(N2∪N3)),
C(G(N3))=C(G(N1∪N3))∩
C(G(N2∪N3)),
dim(κG(N1∪N3)∧κG(N2∪N3))=
rank(A(G(N3)))。
证明由G(N1∪N3)和G(N2∪N3)是G的两个导出子图,可知C(G(N1∪N3))⊆C(G),C(G(N2∪N3))⊆C(G),故C(G(N1∪N3))∪C(G(N2∪N3))⊆C(G)。相反地,由N3分离N1和N2,所以任意一个完全的顶点集N4一定包含在N1∪N3或N2∪N3中,即
C(G)⊆C(G(N1∪N3))∪C(G(N2∪N3))。
同理,可证得
C(G(N3))=C(G(N1∪N3))∩
C(G(N2∪N3))。
由文献[1,5]中
κG(N1∪N3)∧κG(N2∪N3)=κG(N3),
dim(κG(N3))=dim(IA(G(N3)))=rank(A(G(N3)))
可得
dim(κG(N1∪N3)∧κG(N2∪N3))=
rank(A(G(N3)))。
接下来考查一般的离散无向图模型。
定理1G为一个无向图,则rank(A(G))=d′+1。
证明由于零理想是全维的,根据引理1和文献[5]中引理4.2,只需考虑非完全的无向图。同样用归纳法对此定理进行证明。当|C(G)|=2时,结论显然成立。现假设该结论对所有完全集个数不少于k个的图也成立,当|C(G)|=k+1时,考虑以下两种情况:
情况1G可约。假设G=G(N1)⊕G(N2),由于N1∩N2是完全的,所以
C(G(N1∩N2))=C(G(N1))∩C(G(N2))。
文献[1]中的引理2.23证明了κG=κG(N1)∪κG(N2),故
C(G)=C(G(N1))∪C(G(N2))。
由引理1,可得
rank(A(G(N1∩N2)))=
结合归纳假设,有
利用1.3节提及到的公式,可得
rank(A(G))=rank(A(G(N1)))+
rank(A(G(N2)))-dim(κG(N1)∧κG(N2))=
情况1证毕。
情况2G是素的。通过给G添加一些边,可使得此图可约,新的可约图记作G′,且G′=G′(N1)⊕G′(N2),即(N1N2,N2N1,N1∩N2)构成了G′的一个真分解。同时,N1∩N2在图G中分离了N1N2和N2N1。由引理2,可得
C(G)=C(G(N1))∪C(G(N2)),
C(G(N1∩N2))=C(G(N1))∩C(G(N2)),
dim(κG(N1)∧κG(N2))=
rank(A(G(N1∩N2)))。
因为|C(G(N1∩N2))|<|C(G)|,结合归纳假设可得
rank(A(G(N1∩N2)))=
情况2证毕,因此定理1在两种情况下均成立。
定理1将文献[1]中的命题4.35推广到一般DUGMs。事实上,DUGMs维数在两种定义上的取值差异在于文献[1]和文献[5]中给出的定义没有考虑与参数向量对应的归一化常数。文献[6]中的引理2表明可自由设定的参数向量和一个DUGM中的正概率分布存在着一一对应关系。
3 结语
模型的维数问题对于检验、模型选择和分类都具有重要意义。本文证明了DUGMs维数的两种定义本质上是一致的,即计算DUGMs维数有一个简单公式。
