例谈挑战性学习任务在小学数学教学中的运用

山东省威海市第二实验小学 夏建华

《义务教育数学课程标准 (2011 年版)》中提出:学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动。因此，教师要努力去创设挑战性学习任务，在把握好挑战性任务难度的同时，让挑战性任务具有探究性、综合性、开放性，让学生在认知冲突、认知遇阻、认知失衡中体验学习，提升学生的认知能力和学习能力。挑战性学习任务，可以是一个（或几个）具有较大思维空间的问题，也可以是一项（或几项）具有挑战性的活动，还可以是一道（或一组）综合性的习题等。这些挑战性学习任务，往往具有“非常规性、非即时性、非单一性、非安然性”等特点。那么，教师在教学中如何设计驱动性问题、运用挑战性学习任务进行有效教学呢？笔者以单元整体教学理念引领下的四年级上册第四单元《探秘多边形》为例，谈自身教学实践的尝试与思考。

一、创设探究性任务链，提升思维结构

任务链，是将一个大挑战性任务分解成若干个小挑战性任务，这些小挑战性任务之间具有内在的逻辑关联，像链条一样彼此衔接、勾连。在这一探究过程中，学生的思维会不断进阶，结构逐步趋于完善。

四年级上册第四单元《探秘多边形》中关于“高”的教学，一直都是难点，教师教得辛苦，学生学得迷糊。教材原来的编排是分散在不同课时进行学习：信息窗1中先认识三角形的底和高；信息窗3 中再认识平行四边形和梯形的底和高。我认为这样的结构编排并不利于学生对高的本质把握，依据单元整体教学理念，我创造性地将这三种平面图形的高融合在一课时进行探究，并设计如下递进性问题学习任务链，引领学生在解决“问题串”的过程中，让探究逐渐走向深入，接近数学的本质。

《认识底和高》任务链

第一链：由“树高”引入到“三角形的高”

①这里有一棵小树，你认为从哪里到哪里才算是树的高？

②现在刮台风树歪了，跟原来相比，此时的树变高了还是变矮了？这时的树高，指的是从哪里到哪里的高度？

③小树有高度，那三角形有高吗？（出示三种三角形：锐角三角形、直角三角形、钝角三角形）请你尝试在图中画出来。

④你觉得给三角形画高，你可以联想到以前学过的什么类似的知识？

第二链：由“桥高”引入到“梯形、平行四边形的高”

①一辆货车正在公路上行驶，前面有一座桥，限高4.5 米。这里的高4.5 米，指的是从哪里到哪里的距离？只有这一条高吗？你觉得会有多少条这样的高？为什么？

②桥有高度，那梯形有高吗？（出示梯形）请你尝试在图中画出来。梯形的高，只有这一条吗？你觉得会有多少条这样的高？为什么？梯形的这两条腰上也有高吗？为什么？

③平行四边形有高吗？（出示平行四边形）请你尝试在图中画出来。平行四边形的高，只有这一条吗？你觉得会有多少条这样的高？为什么？平行四边形的这两条对边上也有高吗？为什么？

④你觉得给梯形和平行四边形画高，这让你联想到以前学过的什么类似的知识？

第三链：整合关联，凸现异同——寻找高的本质

①对比这3 种平面图形的高，你有什么发现？它们的相同点是什么？不同点是什么？

②我们今天学习的底和高，对今后的学习有什么用呢？

生活经验是学习的起点，由真实情境“树高、桥高”引入三角形的高、梯形的高、平行四边形的高，符合学生的认知规律。通过对比，学生会发现“高”的本质就是之前三年级学习的“点到直线之间的垂直线段”，此时只是把它放在了图形中而已，这是这三种高的相同点；不同点是三角形的高是指点到直线的垂直线段，而梯形和平行四边形的高则是指平行线之间的垂直线段。梯形与平行四边形的高，共性中也有个性的体现：梯形因为只有一组对边平行，所以只有一种长度的高，而平行四边形因为有两组对边平行，所以可能会有两种长度的高。这样，一节课中同时呈现三种平面图形的高，有利于学生经历完整的问题探究过程，通过对比，发现异同，归纳本质，提升思维结构层级。

二、创设“三学”化任务单，优化学习结构

学习任务单，是学习支架的主要形态，是教师依据学情，为达成学习目标而设计的学习活动的载体。同一内容，在不同的时间段——学前、学中、学后，根据承载的侧重点不同，可以设计一系列的学习任务单，以期优化学生的知识结构。

学前单，即在课堂学习前设计的学习任务单，重在读懂学生，了解学生已有什么，还需什么，能学什么，明确学生认知起点在哪里，认知目标到哪里，认知路径是什么，从而真正实现因材施教和学习结构重组。

第四单元《探秘多边形》中关于《三角形的内角和》一课，教师设计了这样一份学前任务单：

《三角形的内角和》学前单

同学们，我们已经知道三角形根据角来分，可以分为锐角三角形、直角三角形、钝角三角形。

[提出猜想]三角形的内角和可能是______度？

[操作验证]我们用不同类型的三角形来研究一下吧。

你想用什么方法来验证你的猜想？将你的验证过程用你喜欢的方式呈现出来。

[得出结论]__________________。

[反思评价]除了上述这种方法，你还想到了什么方法也可以验证?

通过你的操作验证，你还有什么发现？还有什么困惑？

学中单，即课堂学习中设计的学习任务单，重在学法指导，调控关联活动，培养高阶思维。通过设计挑战性学习任务，以核心知识学习为原点，学生通过探究自主发现相关、相近的知识元素的关系，形成“连点成线、由线成面”整体融通的知识体系。

在《三角形的内角和》一课中，教师设计了这样一份学中任务单：

《三角形的内角和》学中单

同学们，现在我们已经知道了三角形的内角和是180°。那么，四边形的内角和是多少度？它与三角形的内角和有没有关系？小组合作，共同探究。

[提出猜想]四边形的内角和可能______度？

[操作验证]我们用不同类型的四边形来研究一下吧。

你们想用什么方法来验证你们的猜想？将你们的验证过程用喜欢的方式呈现出来。

[得出结论]___________________。

[反思评价]四边形的内角和与三角形的内角和有什么关系？为什么会有这种关系？

（长方形、正方形、平行四边形、梯形……）

学后单，即课堂学习后设计的学习任务单，重在迁移运用，一是体现内容迁移，学习的最终目的是运用，在运用中加深理解，促进思考，使思维向广度与深度两个方向发展；二是体现分层选择，根据学生的个性差异，对课后学习任务进行分层设计，学生可以根据自己的兴趣和能力选择不同的挑战性任务。

在《三角形的内角和》一课中，教师设计了这样一份学后任务单：

《三角形的内角和》学后单

1.回顾：通过今天的学习，你都学会了用哪些方法来验证“三角形的内角和是180°”？请你写一写或画一画。

2.练习：

①李明今天过生日，爸爸送给他一个等腰三角形的风筝，它的一个底角是70°，它的顶角是多少度？

②画一画，算一算，你发现了什么？

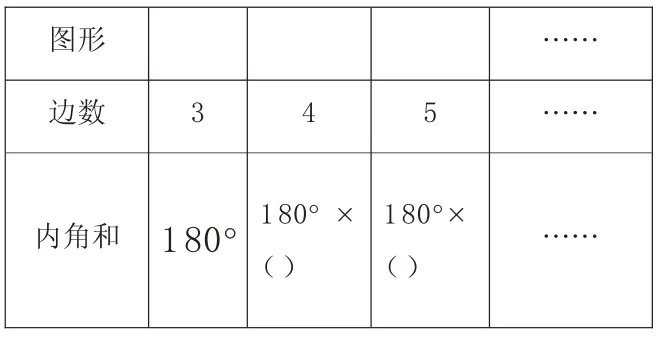
我的发现：___________________。

3.拓展：（二选一）

①课外阅读《帕斯卡与“三角形内角和”的故事》。

你看明白了吗? 怎么证明钝角三角形的内角和也是180 呢?赶紧找个三角形试一试吧!

②绘本赏欣《失落的一角》。

通过赏析，你有什么感想？

“三学”任务单与学习活动的一体化应用，充分体现了“学为中心”的教育理念，不同的生活情境、数学情境的创设，促使了学生学习的高投入，高认知，促使“真学习”的发生。

三、创设开放性任务群，完善认知结构

学习任务群，指以任务为导向，以学习项目为载体，整合学习情境、学习内容、学习方法和学习资源，通过一定的实践活动将这些因素建立起联系，从而建构知识和学习体验，完成相应的任务，提升素养。

第四单元《探秘多边形》中，按教材的编排全部结束所有的内容之后，为了拓宽学生的视野，提升思维的灵动性，我增设了一节拓展课——《百变多边形》。通过创设开放性任务群，让学生在实践活动中玩转各种图形，感受图形的变幻，探寻图形之间的关联，进而完善认知结构。

活动一：巧板36 变

学具准备：每小组提供一套“七巧板”。

任务1：从七巧板中选取其中的三块板拼成一个平行四边形。

任务2：从七巧板中选取其中的三块板拼成一个三角形。

任务3：从七巧板中选取其中的三块板拼成一个梯形。

任务4：先利用七巧板的七块板拼成一个大三角形（如上图所示），再只能动一步，将这个大三角形变成平行四边形。

活动二：图形魔术

学具准备：每小组提供2 张相同的平行四边形纸片、2 张相同的三角形纸片（锐角三角形、直角三角形、钝角三角形中的一种）、2 张相同的梯形纸片。

任务1：将一张平行四边形纸剪成两部分，再拼成一个长方形。①说一说你是怎样剪拼的？有几种拼法？②拼成的长方形与原来的平行四边形有什么关系？

任务2：选择一个或两个完全一样的三角形，通过怎样的操作可以将其转化为我们学过的图形？转化后的图形与原来的图形相比，有什么关系？

任务3：选择一个或两个完全一样的梯形，通过怎样的操作可以将其转化为我们学过的图形？转化后的图形与原来的图形相比，有什么关系？

开放性的学习任务群，通过知识的条件化、情境化、结构化，给学生的思维发展创设了更为宽广的空间，让不同思维水平的学生都能获得探索的机会和成功的愉悦，既丰富了学生的学习活动经验，又实现了学生对知识的深度理解，进一步完善了认知结构。

数学虽注重理性思维培养，但数学学习也是有温度的。在任务驱动式小学数学教学中，教师应为学生搭建一个以知识结构为载体，情意结构为动力，思维结构为核心，认知结构为发展的立体式结构，设计带有挑战性的学习任务，激发学生主动探究的欲望，通过自助、互助，引发学生自身深度思考，使其知识结构合理转化、情意结构逐步细化、思维结构持续深化、认知结构完善优化，驱动结构化思维，促使深度学习的发生。