高速列车单列通过时双线隧道内列车风分布规律研究

管鸿浩,龚彦峰,踪敬良,焦齐柱,耿语堂

(1.中铁第四勘察设计院集团有限公司,武汉 430063； 2.水下隧道技术国家地方联合工程研究中心,武汉 430063； 3.中南大学轨道交通安全教育部重点实验室,长沙 410075)

引言

随着列车速度不断提高，列车运行时产生的瞬时气流对轨旁工作人员安全及轨旁基础设施造成威胁[1-3]。迄今为止，对于列车在露天中的列车风已进行了全面研究[4-6]，GILBERT等[7]通过动模型试验及露天控制实验发现，在隧道中阵风峰值比露天条件下高。这也使越来越多的人将注意力转移到列车-隧道耦合的空气动力学效应上。

由于地理环境原因，为满足线路技术标准要求，隧道在高速铁路工程建设中必不可少。在国内外已投入运营的高速铁路中，隧道长度均占了较大比例。日本山阳新干线隧道占线路总长50%，北陆新干线更是达到了63%。我国山地较多，高速铁路隧道数量众多、分布广，如石太客运专线隧道长度占线路总长的39.4%，其中，全长27.8 km的太行山隧道是目前我国建成通车最长的铁路山岭隧道；温福客运专线总长298 km，全线建有双线隧道59座，隧道长度占线路总长的50.1%。从“十一五”至“十三五”期间，我国建成高速铁路隧道9 260座，总长约为15 316 km，已成为全世界拥有高速铁路隧道最多的国家。

由于隧道的半封闭性，当列车由空旷地带高速驶入隧道时，车体附近的空气被迅速排开，被排到一边的空气不能像在露天那样及时释放，空气只能向列车前方或后方流动。当列车车头进入隧道时，车头前方会形成高压区，推动空气向前流动。当列车尾部进入隧道时，尾部会形成低压区，将空气吸入隧道内，这种效应被称为活塞效应[8]。SHIN等[9]对列车在隧道中运行时的流动特性进行了数值模拟；费瑞振等[10]采用数值模拟方法计算隧道内两侧疏散通道上不同位置在列车运行过程中的最大风速，分析了在列车风作用下人员的安全性；刘堂红等[11]对隧道内列车风进行了实车试验研究，发现隧道内列车风风速与列车运行速度呈线性关系。相对于单线隧道的列车风交会工况，列车风增幅可达1.6倍[12]。谭鹏等[13]采用数值模拟方法对列车在城际铁路隧道内运行过程中所产生的列车风变化过程进行分析，计算流线型高速列车在隧道内运行时，隧道内沿纵向不同位置列车风最大风速，进一步对隧道内列车风纵向和横向分布特性进行了探讨。关于活塞风的特性以及计算方法方面，李炎等[14]提出了活塞风压力和活塞风速度的计算方法；王丽慧等[15]通过现场实测，研究了地铁出站情况下活塞风对地铁车站各个单元速度场的影响；LIU等[16]通过建立活塞风理论模型，研究了5个因素对活塞风速的影响，发现堵塞比对活塞风量影响最大。活塞效应所形成的列车风严重影响隧道内设备安装稳定性，对维修人员及列车运行安全性造成影响。高龙等[17]基于隧道气动效应等指标进行检测，分析列车风对于列车运行平稳性的影响；雷波等[18]根据列车风场的特点，提出一种计算列车风作用于人体气动力的方法。上述文献中多采用滑移网格技术对列车风进行研究。

目前，针对隧道内列车风主要是机理方面研究，关于列车风的分布规律研究相对较少，但在列车和隧道不同因素的交织影响下，列车隧道运行时产生的列车风比明线运行时更复杂，且由列车风产生的动压会对安装在隧道内的辅助设施产生瞬态压力冲击，影响隧道内辅助设施安装稳定性，严重时会导致承压件表面损伤，悬挂件掉落等问题。因此，亟需开展隧道列车风以及动压研究。本研究对单列列车以350 km/h速度通过双线隧道情况下的列车风及动压进行分析。使用数值模拟方法，运用RNGk-ε湍流模型，采用商业CFD软件ANSYS-FLUENT，分析列车通过隧道时不同位置处纵向、横向和垂向方向3个分量下的列车风速度及动压分布规律。

1 数值方法

1.1 几何模型

本次计算所采用的列车模型为全尺寸复兴号动车组，由8节车组成，分为头车、6节中间车以及尾车，如图1所示。其中，头车与尾车长度均为27.5 m，中间车每节车长度为25 m，总长205 m，列车宽3.36 m，高4.05 m。列车计算模型具有大部分的一般形状特征，包括转向架风挡等。为获得更高的网格质量，提高计算效率，计算模型忽略了受电弓及其他附属结构的影响。计算隧道为双线隧道，横截面积为100 m2，如图2所示，列车车轮下边缘距离地面高度为0.2 m，用来模拟轨道高度，轨间距为5 m。列车运行在y轴正方向的一侧，隧道长度选取最不利隧道长度，采用式(1)计算。

图1 列车模型(单位：m)

图2 隧道断面(单位：m)

(1)

式中，Ltu，crit为最不利隧道长度；Ltr，A为第一列车长度；Ltr，B为第二列车长度；c为声音传播速度(取340 m/s)；vtr，A为第一列车运行速度；vtr，B为第二列车运行速度。

通过式(1)计算出两车交会情况下的最不利双线隧道长度，由于目前隧道多采用双轨隧道结构，因此，选用双线最不利隧道长度进行研究。当列车运行速度350 km/h、车长205 m时，双线隧道最不利长度为716.9 m。本次数值模拟计算模型为全尺寸模型，与实际情况相同，因此，对应雷诺数Re=2.9×107。

1.2 计算域与边界条件

单列列车通过双线隧道的计算域如图3所示，计算域分为隧道域和外域，为保证外域的尺寸足够大，将外域设置为两个相同的长400 m，宽80 m，高40 m的长方体，可保证隧道入口附近的流动不受外部环境影响。列车位置在图3中已进行了标注，为保证列车从露天区域突然进入隧道时的稳定性，列车放置在距隧道入口50 m的位置。边界条件示意如图4所示。整个计算区域被划分为2个区域，区域A为滑动区域，区域B为静止区域。区域A是一个细长的长方体滑块，包含计算所用列车。区域B包含外域和部分隧道域。列车与隧道之间的相对运动采用滑动网格技术实现，滑动网格计数是目前公认的模拟列车和隧道相对运动最为方便有效的方法之一，利用区域A的移动边界来模拟列车，运动。由于在使用滑动网格技术时，网格质量和计算速度是两个需考察的重要因素，与动网格技术相比，滑动网格无需网格再生的特性具有独特的优势，既不降低网格质量，同时又大幅提升了计算效率。

图3 计算域示意(单位：m)

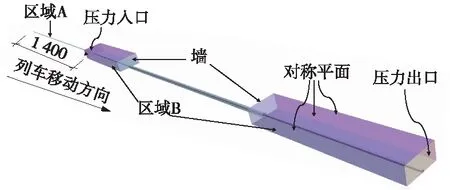
图4 边界条件设定(单位：m)

将列车表面、地面、隧道、外域前端定义为静止防滑墙边界。为保证计算外流场的完整性与准确性，滑动区域末端超出静止区域末端1 200 m，从而保证了列车在驶出隧道后，滑动区域末端不会进入静止区域。坐标系原点位于隧道入口地面。X轴为隧道长度方向即纵向，Y轴为隧道宽度方向即横向，Z轴为隧道高度方向即垂向。

1.3 网格模型

由于列车计算模型大部分具有一般形状特征，包括转向架风挡等，滑动区域的网格靠近车体部分采用非结构网格进行离散。远离车体的滑动区域和静止区域由于其具有相对规则的几何边界，其网格采用更加优秀的结构网格，所述滑动区域与静止区域网格如图5所示。靠近列车表面的网格尺寸为0.008 m。由于列车前端和尾流部分与压力和风速高度相关，因此，对这些区域进行了细化。

图5 网格方法

1.4 监测点设置

隧道段设有17个测量点，用以监测隧道内列车风。靠近隧道墙的测量点位于距轨道中心6.0 m处。由于监测点易受地面影响，在距离地面1.0 m和2.0 m处分别设置1个监测点，其余监测点沿高度方向间距为2.0 m。为监测隧道顶部的列车风情况，在距离地面高6 m的位置靠近列车一侧，隧道中线位置，远离列车运行一侧共设置3个测点。针对单列火车通过双线隧道的情况，隧道内列车风沿隧道中心线不对称。因此，在横向距离列车较远的一侧，共设置8个点，横向间隔2.0 m。具体检测点如图6所示。

图6 监测点布置(单位：m)

1.5 求解器设置

由于波效应与活塞效应的存在，当列车高速通过隧道时，列车周围的流动呈现出高度的紊流非定常状态，雷诺应力模型和涡黏性模型中的k-ε两方程模型在列车周围空气流场流动的湍流数值模拟中应用最为广泛。考虑到隧道内为密闭空间以及马赫数大于0.3，湍流模拟采用三维可压缩的RNGk-ε湍流模型来求解隧道内的复杂流动。该模型已被广泛验证，可有效模拟列车在隧道中通过所产生的空气动力学效应[19]。控制方程采用Navier-Stockes方程和能量方程，有关于控制方程的相关介绍可在CHU等[20]研究中获得答案。

采用FLUENT商业软件对上述方程进行求解，采用有限体积法(FVM)进行离散，对流扩散项采用二阶迎风格式，速度-压力耦合方程求解基于SAMPLE算法，时间项处理采用非定常模拟的二阶隐式格式，列车在0.51 s进入隧道，在10.0 s驶出隧道，时间步长设置为0.008 5 s，总计算时间为11.0 s，整个计算需要时间步超过1 200步，每个时间步长迭代次数为50次，所有的计算数据通过用户自定义函数(UDF)文件进行输出。

1.6 数据处理方法

为使后续数据对比及分析结果更加方便，使用无量纲系数处理数据。在本研究中纵向、横向和垂向分量的无量纲列车风速度定义为u/V、v/V、和w/V，其中，V为列车运行速度，无量纲合成列车风速度为VR，结合上述3种速度分量，其定义为

(2)

2 网格无关性验证

为验证本研究采用的网格方案足够成熟，使求解误差最小化，通过细化网格进行网格无关性研究。分别生成粗网格和细网格2种不同尺度的网格，分别有约2 600万个和3 800万个网格单元。2种不同网格的详细参数如表1所示，主要优化实现在转向架、列车车身和隧道表面。选择隧道左侧的不动点x=250 m，对比该点列车风的纵向分量和压力，如图7所示。结果表明，与细网格相比，粗网格的最大列车风预测值偏差较小，偏差约为1.0%，最大压力系数预测值偏差为0.9%。因此，为保持较高精度的同时减少计算资源，采用约2 600万个网格单元的粗网格方案。

表1 网格详细参数

图7 不同网格计算结果对比曲线

3 结果与分析

3.1 隧道内列车风时间与空间演变

隧道空气动力学在本质上是瞬态变化，不同位置、不同时间段测点数据都会有较大不同。选择3个具有代表性的位置x=150，350，650 m分析隧道内列车风的时间与空间演变。这3点分别位于隧道入口附近、隧道中部、隧道出口附近，其横向及垂向坐标全部为y=6.0 m、z=2.0 m。图8为3个测点的列车风时程曲线，如图8(a)所示，在隧道入口位置，隧道内列车风受活塞效应影响，列车风速度逐渐增加，在列车经过测点位置时，环状空间内列车风迅速降低并改变方向，尾车通过测点时达到负峰值；列车经过后，列车风迅速改变方向，并逐渐增加至正峰值。与纵向分量不同的是，横向分量和垂向分量在列车未到达时，速度稳定为0，在头车到达时，横向分量和垂向分量产生正向波动。随着尾车经过，横向分量产生负向波动，但垂向分量受尾车的影响产生正向波动。

在隧道中部位置，列车风变化与隧道入口处基本一致，只是在时间上有所延迟。由图8(c)可明显看到，在列车未到达时，隧道内列车风经过了先增大后减小再增大的过程，这是由于隧道内压力波会对局部气流造成影响。当头车或尾车突然进入隧道时，由于挤压作用产生压力波，当压力波在进口或出口传播时，压力波被反射，强度降低。当不同的波相遇时，会发生波的叠加和抵消效应，这会导致局部压力波动和复杂的气流变化，具体可在LI等[21]研究中得到解答。

图8 列车风时程曲线

对于VR的3个分量，纵向分量u占据主要成分。根据VR的计算公式，横向分量v和纵向分量w值相对于u都较小，取平方根后可忽略不计。因此，VR的极值近似等于纵向分量u的极值。由于隧道内列车风主要以纵向分量为主，纵向分量u与合成列车风VR基本一致，故研究更多集中在纵向分量u。

隧道内列车风是三维的，同一截面不同位置处列车风速度有较大区别。图9给出了在x=350 m截面处，不同测点的列车风曲线，有针对性地分析隧道顶部列车风变化规律，测点高度z=6 m，测点位置分别在列车运行一侧、隧道中心线、远离列车一侧。由图9可以看出，在列车经过时，隧道顶部列车风速度小于轨道旁边列车风速度，这是由于测点距离列车位置较远所导致。通过对比可知，列车经过时，列车风速度在同一截面不同位置处相差并不大；列车经过后产生较大不同，靠近列车运行一侧的列车风速度远大于隧道中线以及远离列车运行一侧列车风速度；在隧道中线位置以及远离列车运行一侧，列车风速度几乎没有差别。

图9 隧道顶部列车风时程曲线

表2为测点位置列车风速度峰值，可以看出，列车经过时，靠近列车一侧、中线位置及远离列车一侧列车风速度负峰值相差不大，但正峰值明显不同，靠近列车运行一侧与隧道中线及远离列车运行一侧有较大区别，这是由于算例为双轨铁路隧道，列车运行在隧道偏中心一侧，列车周围左右空间不对称。左侧较快气流和右侧较慢气流在尾迹区相遇，产生压力差，将空气吸入左侧。进一步发展后，在远尾迹区域形成速度层，高速度向靠近列车一侧倾斜，低速度向远离列车运行一侧倾斜。这一现象可通过图10所示尾迹区列车风速度云图得到验证。

表2 列车风系数峰值

图10 尾迹区列车风速度系数云图

3.2 隧道内列车风峰值分布

无论是在横向或垂直方向上，露天列车风的强度和最大值与距车身距离强相关[22]。由上一节可以得到，隧道中线位置与远离列车一侧位置列车风速度相差较小，这一点将在本节展开讨论。

图11(a)为隧道内x=350 m、z=2 m时，横向不同位置处列车风纵向分量时程变化曲线。可以看出，在列车到达测点前，不同位置处列车风基本一致，在头车到达时，隧道中线位置处会有相对较小的向上波动，但其他位置并无波动；列车经过时，列车风速度迅速下降，改变方向，列车通过的时间内，列车风速度始终为负方向，且随着列车经过，列车风速度逐渐增大，在尾车通过时，速度达到负峰值；列车通过后，不同位置处的列车风呈现出明显不同，隧道中线附近，随着列车经过，列车风速度转变为正值后，达到了列车风速度正峰值。但远离列车运行一侧，随着列车的经过，列车风速度逐渐趋近于0，波动较隧道中线位置明显减小很多；列车通过隧道后，隧道内列车风速度随着与列车距离的增大而减小。图11(b)为列车风峰值沿y方向分布规律，可以看出，当距离隧道中线超过4 m后，列车风峰值基本保持不变，这是由于车尾经过时所引起的尾流对远离列车一侧影响较小，其影响程度小于列车未经过时活塞作用下所引起的列车风，因此远离列车运行一侧的列车风峰值基本相同，而隧道中线位置由于距离列车较近，其列车风强度受列车尾流影响较大。这些可通过图12的列车风速度云图得到验证。

图11 列车风的横向分布曲线

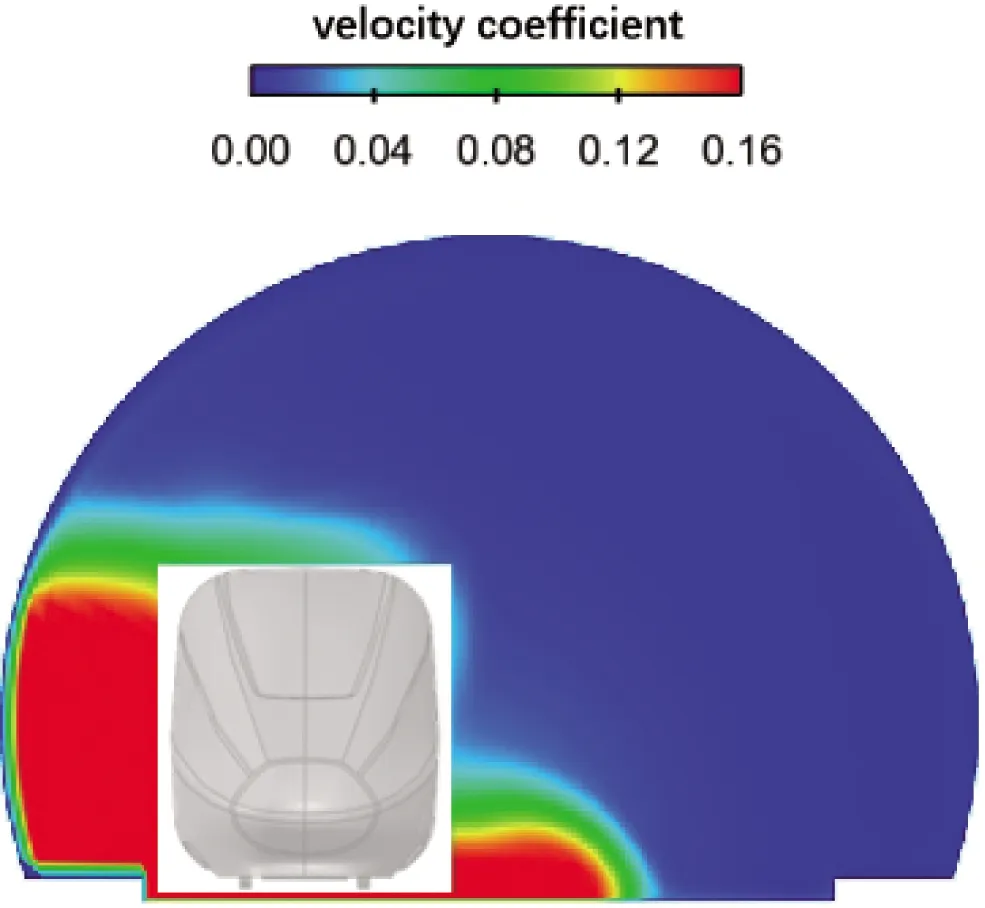
图12 x=350 m处列车风速度系数云图

垂向高度也是影响列车风峰值的另一个重要因素。图13(a)为纵向列车风分量u在x=350 m隧道中线位置离地面不同高度时的时间历程曲线。可以看出，在z=1 m时，列车风速度明显较其他位置大，而随着高度不断增加，列车风变化的波形基本相同。值得一提的是，局部气流在列车到达前已经上升，且不同高度波形与幅值均相同，这一点与不同横向距离的表现一致。可以认为，在列车到达前，隧道内的列车风速度也具有较强的一维效应，随着列车到达，这种一维效应被打破，从而表现出列车风三维特征。图13(b)为不同垂向高度列车风峰值分布规律，可以看出，从垂向高度1 m到垂向高度2 m纵向列车风速度峰值迅速下降，在垂向高度大于2 m后列车风速度峰值差别较小。这是由于受车头、转向架和车底设备影响，底部区域气流非常湍急；而中间区域及列车顶部，列车风峰值下降得很慢，这是由于测点位置在隧道中线位置，远离列车运行一侧空间广阔，且受移动列车影响较小。

图13 列车风的垂向分布曲线

3.3 隧道内动压峰值分布

众所周知，空气做定向流动时具有动能，而当物体处在流体中时，在正对流体运动方向的表面，流体完全受阻，此处流体速度为0，其动能转变为压力能，其所呈现的压力称为动压。通过前一节分析可以发现，隧道内列车风在靠近列车运行一侧达到最大值，而远离列车运行一侧列车风速度相对较小，因此，动压分析主要针对靠近列车一侧距离隧道中心线y=6.0 m，z=2.0 m位置。根据动压计算公式P动=ρv2/2，获得隧道内各位置处动压峰值，其中，P动为隧道内各位置处的动压值；ρ为空气密度；v为测点位置风速。通过计算可以得出，隧道内不同位置处的动压峰值，如表3所示。由表3可知，在隧道入口位置，由于列车并没有完全进入隧道内，隧道内流动并未完全形成，动压相对较小。而当列车完全进入隧道后，动压值相对基本稳定在1 000～1 300 Pa，因此，在设置隧道内附属设施时，应相应考虑动压所带来的影响。

表3 隧道内不同位置动压峰值

4 结论

采用三维、可压缩、非定常的Navier-Stokes方法全面研究单车通过双线隧道时，隧道内列车风以及动压的分布规律，为隧道内附属设施安装及维修人员安全避让提供数据参考。主要研究结果如下。

(1)纵向分量在隧道内列车风中占主要成分，列车所诱导的列车风纵向分量u变化与产生的列车风VR变化基本一致，且纵向列车风分量受到隧道内压缩波及膨胀波的影响产生较明显的波动，列车风横向分量和垂向分量值相对较小。

(2)靠近列车运行一侧列车风峰值出现在列车尾部经过时，而远离列车运行一侧列车风峰值出现在列车未到达时，主要由于单列车在双线隧道内运行时，列车与隧道壁之间空隙不一致导致。

(3)在列车到达前，同一截面位置处的列车风表现出较强的一维效应，列车风速度相同，在列车到达时，一维效应被打破，表现出明显的三维效应。在远离列车运行一侧，当距离隧道中线超过4 m后，列车风峰值基本保持不变，仅距离列车较近位置的列车风强度随着横向距离增加逐渐减小。横向方向在远离列车运行一侧，当距离隧道中线超过4 m后，列车风峰值基本保持不变。垂向方向在隧道中线位置，从垂向高度1 m到垂向高度2 m纵向列车风速度峰值迅速下降，在垂向高度大于2 m后列车风速度峰值差别较小。

(4)在隧道入口位置，由于列车并没有完全进入隧道内，动压相对较小，而当列车完全进入隧道后，动压值基本稳定在1 000～1 300 Pa。