地铁列车运行引起地面住宅振动烦恼率研究——以某城市地铁线路对应地面住宅为例

周俊召,张天琦,王迪瀚,陈浠航

(1.同济大学铁道与城市轨道交通研究院,上海 201804； 2.上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)

地铁具有运量大、时效性强、绿色环保等优点，在城市公共交通中扮演越来越重要的角色。我国城市大多是发展到一定规模后再修建地铁，增大了地铁选线工作的难度。在选线中既要考虑整体规划的要求，又要控制成本，这就导致随着地铁的建设发展，不可避免地对周边居民带来影响，因地铁运行引起的地面建筑振动与噪声近年来引起了广泛关注，特别是对居民楼等敏感建筑的影响。振动被列为世界七大环境公害之一，其对人体的影响是多方面的，一定强度的振动影响人们的正常休息和工作，甚至引发生理上的不适[1]。人体将前庭觉、视觉、躯体觉和听觉系统的信号组合起来感觉振动[1]，经验表明，居住建筑的振动水平稍微超过人体的感知水平时，居住者就会产生不满[2]。

有关地铁运行对地表建筑的振动研究，国内外学者开展了一系列工作。马蒙等[3]将既有的现场实测与数值模拟相结合，进行轨道交通振动对建筑物影响程度的预测；周巍等[4]结合工程实际，进行了城市轨道交通环境中既有建筑室内振动隔振方法的研究；施毅等[5]采用文献[8]中烦恼率模型进行了地铁列车进出站相邻地下空间振动评价；丁浩民等[6]通过建立有限元模型，结合烦恼率模型，进行了地铁引起建筑物振动舒适度的分析；张晓春等[7]同样采用烦恼率模型，结合建立的有限元模型，进行了地铁列车振动对临近建筑内人体舒适度的影响研究；宋志刚等[8-10]基于模糊理论建立了烦恼率模型；部分学者采用烦恼率模型进行了不同领域的振动舒适度评价[11-17]；RÜUCKER[18]通过建立有限元模型，分析了地铁运行时不同隧道深度所产生的振动辐射变化规律。现有研究多集中在地铁运行下地标建筑的振动响应，或是通过建立有限元模型结合烦恼率进行地铁运行地面建筑舒适度的研究，而针对地铁列车运行条件下对应的地面住宅振动烦恼率的实地试验研究较少。为获取相关结论，有必要进行实地试验和烦恼率的计算研究。

1 测试分析

1.1 测试条件与测点布设

为对地铁列车运行引起地面住宅振动烦恼率进行研究，首先要进行现场测试。现场振动测试选取某城市某轨道交通线路对应的地面住宅，试验断面对应的地铁线路为R=500 m的曲线段，轨下为浮置板道床，振动加速度数据采集的建筑底部距隧道上边线最小距离为14.2 m，距轨顶面最小距离为19.1 m，振动数据采集房间为卧室，使用量程为0.5g的振动加速度计，以铅垂向为主要方向，按照振动测试要求，室内振动测点呈三角形布置，图1为室内振动测点布置示意。

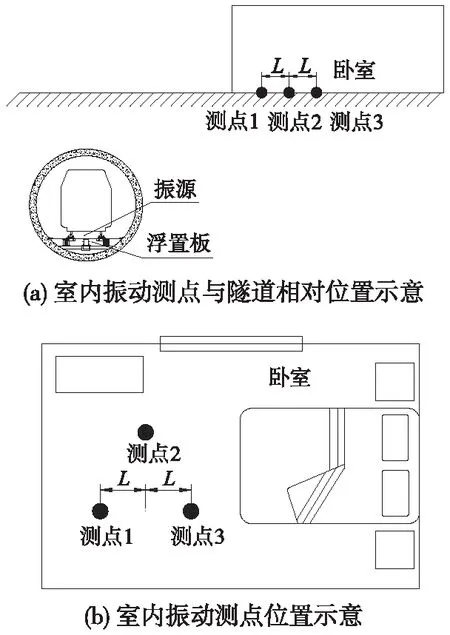
图1 室内振动测点布置情况示意

1.2 测试结果分析

根据文献[19]以及人体的反应，振动对人体影响的主要频率范围在1～80 Hz，其间以1/3倍频程来划分，同时对建筑内振动限值进行了限定。考虑到列车夜间运行对住宅内的居民影响较大，因此，选择夜间进行测试，分析截取地铁列车通过所测断面的全程时间，相关标准对比取值也取对应的夜间限值。图2为3个振动测点测得的典型加速度时程谱。

图2 室内3个振动测点典型加速度时程谱

对测试结果进行处理，建筑物振动评估参考标准选取GB10070—88《城市区域环境振动测量标准》、JGJ/T 170—2009《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》与DB31/T470—2009《城市轨道交通(地下段)列车运行引起的住宅室内振动与结构噪声限值及测量方法》。根据标准JGJ/T 170—2009规定，需对室内垂向加速度信号1/3倍频程中心频率进行Z计权处理，按计权因子修正后得到各中心频率的振动加速度级，按标准GB10070—88选择振动计权加速度级VL进行评估分析，其计算公式如下

(1)

式中，VL为振动计权加速度级,dB；VALi为每个频带的振动加速度级,dB；ai为各个频带的计权因子。标准DB31/T470—2009与JGJ/T 170—2009的评估分析参量均选择1/3倍频程中心频率上的最大振动加速度级(简称分频最大振级，记为VLzmax)进行评估分析。根据规范标准及人体对不同频率振动的感受，分析频率范围为4～200 Hz，对数据进行Z计权，表1为3个测点的等效Z振级与最大Z振级的结果对标评估。

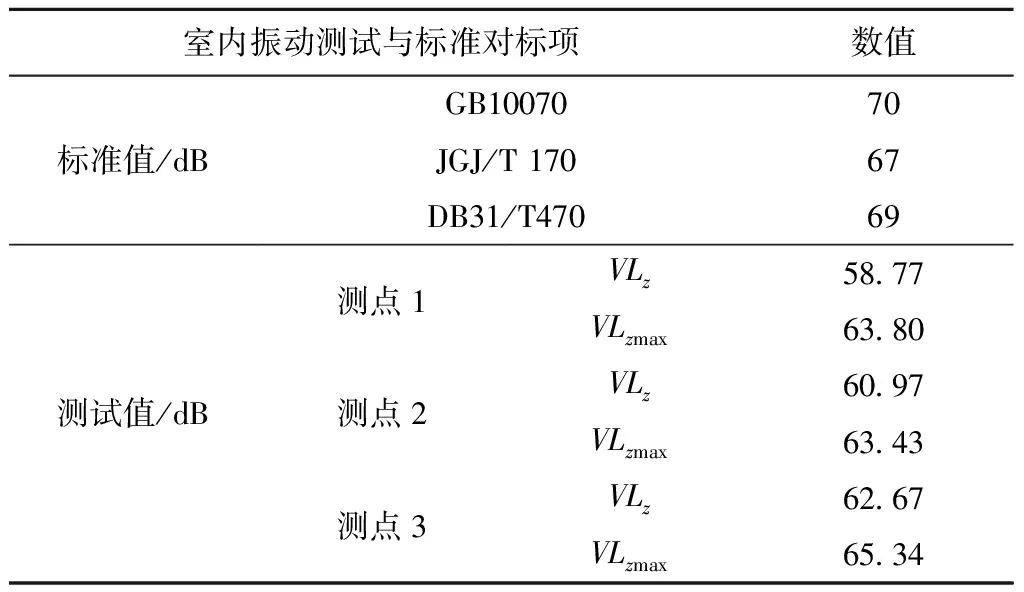
表1 室内振动测试结果对标评估

由表1可以看出，测得的结果均满足相关规范要求，未超过标准限定值，但个别数据接近限值。说明该区段浮置板道床工况下，所选断面对应的地面住宅室内振动符合规范要求，但仍具有个体差异，不同的人对振动的主观判断具有一定的模糊性，且部分居民反映测试区段的室内振动水平“不可接受”。因此，需引入基于模糊模型的烦恼率模型，进行地铁列车运行引起地面住宅振动的烦恼率研究，以获得更为直观的烦恼率。

2 烦恼率模型

烦恼率反映的是在一定振动强度下认为振动“不可接受”的人的比例，能为振动舒适度标准确定烦恼阈值依据。人体对于不同频率的振动敏感度具有差异性，Z向振动的频率计权函数为

(2)

式中，Wz(f)为振动加速度在某个频率的计权系数；当振动频率为f且峰值加速度为amax时，其计权振动加速度为

aw=Wz(f)μ-1amax

(3)

式中，μ为峰值因子，通过统计分析建议μ取2.5[8]。

因振动主观反应判断的标准具有模糊性，离散分布情况下烦恼率的计算公式如下[20]

(4)

根据模糊性和随机性分布的特点，对一个振动强度为aw的烦恼率，连续分布情况下烦恼率的计算公式如下

A(aw)=

(5)

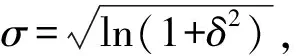
(6)

其中，umin为人体“感觉不到”的强度上限；umax为人体“无法忍受”的强度下限；系数a和b由下式得到

(7)

对于随机分布的加速度信号，烦恼率分布函数可以用对数正态分布函数近似表示

(8)

根据以上理论及公式，可以确定任意经过频率计权的振动强度下的烦恼率。

3 烦恼率计算与讨论

将实地测得各测点的数据进行加速度计权和倍频程分析，获得各测点位置处的垂向振动加速度，对其进行计算得到均方根值并对其进行频率计权，统计结果见表2。

表2 各测点位置处计权加速度均方根值 m/s2

对于一般建筑来说，振动舒适度标准给出的容许下限值为r1，导致人认为“不可接受”的振动加速度为4r1。根据ISO2631—2中定义的倍数表，结合给定的竖向振动舒适度r0=0.005 m/s2，将分析所采用的加速度倍数和加速度计算参数统计于表3，因本次只考虑夜间地铁运行对住宅居民的影响，相关限值也只选取夜间情况，因此，只统计夜间对应的竖向振动数据。

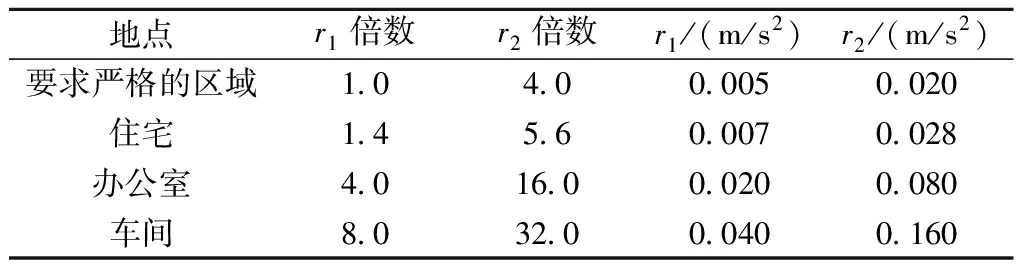
表3 分析所采用的加速度倍数与对应加速度计算参数(夜间垂向振动)

由表3可以得到，不同区域振动舒适度标准给出的容许下限值r1，以及导致人认为“不可接受”的振动加速度为r2，也即对应的umin和umax。将表3中的汇总值代入烦恼率计算模型，可以得到烦恼率模型中的参数a和b的值，见表4。

表4 不同情况下烦恼率曲线计算参数(夜间垂向振动)

本研究主要关注住宅区域，由表4可以得到，烦恼率模型中的a取0.721 3，b取3.579 2，根据a与b的值及烦恼率模型，进一步计算可得到如图3所示的研究现场测试工况下的烦恼率曲线。

图3 住宅夜间垂向振动烦恼率曲线

结合现场测试获得的表2中的数据，将各测点位置处计权加速度均方根值代入计算得到的对应烦恼率模型中，可以得到表5所示的室内振动各测点位置处的烦恼率。

表5 各测点位置处最大烦恼率值

通过使用校准法，给出工程上一般情况下可接受的振动舒适度设计水平对应容许的烦恼率值为7%[8]。由表5可以看出，测点3位置处的最大烦恼率值达到了13.3%，超过了7%的容许值，测点1的烦恼率水平控制在相对较低的水平。说明测点3相比测点1和测点2更接近或更有可能是所测房间的振动敏感点。整体来看，3个测点的烦恼率都处于相对较低的水平，说明浮置板道床对列车通过产生的振动控制效果较好。

根据表1室内振动测试总极值对标评估的内容，可以看出3个测点的等效Z振级与最大Z振级均未超过相关规范标准。但由于不同的人对振动的主观判断具有一定的模糊性，根据烦恼率模型计算得出的结果出现了测点3位置处的烦恼率达到13.3 %的情况，测点2位置处的烦恼率也接近工程上可接受的振动舒适度设计水平对应容许值。因此，在研究范例内，实地测试的振动水平未超过限值，而实际情况下还会有一小部分人认为所处的环境振动水平“不可接受”而投诉，特别是对于抵抗力较弱的老人、儿童以及病人等有特殊要求的人群，符合标准限值但有相对较高烦恼率的振动可能会对一小部分人产生一定程度的影响。

4 结论

通过采用基于模糊模型的烦恼率模型方法对实际测试数据分析，对地铁列车运行引起地面住宅振动烦恼率研究，可以更全面反映振动对住宅区域居民烦恼率影响，结合目前的规范方法，可得到更为详细和客观的分析结果。

通过所建立的烦恼率模型，根据实测数据进行分析，测点3位置处的烦恼率达到13.3%，超过了工程上一般情况下可接受的7%的容许烦恼率值，但按照现有规范还无法反映这一具体情况。

研究表明，在本文的研究范例内，符合目前现有规范要求的振动水平不一定所有点位都有较低的烦恼率，一些部位可能还会对一部分人产生影响，针对这一现象应用并参考烦恼率模型，采取相关措施控制烦恼率处于较低的水平，达到更合理减小地铁列车通过引起的地面住宅振动对居民产生的影响。研究结果可为地铁列车运行引起地面住宅振动的合理控制提供依据。