隧道瞬变电磁克希霍夫偏移成像与地质灾害探测

戚志鹏，郭建磊,2，孙乃泉，李 貅，樊亚楠

(1.长安大学 地质工程与测绘学院，陕西 西安 710054；2.中煤科工集团西安研究院有限公司，陕西 西安 710077)

隧道与巷道超前预报不仅要预报灾害体的存在，更应该确定灾害体的几何结构，判断灾害的成灾性质，为后续的灾害治理提供有效的信息[1]。瞬变电磁法作为一种电磁感应方法，在低阻灾害体隧道超前预报中起到了预警的作用，避免了重大灾害事故的发生。但是随着绿色工程施工的提出，在地下工程建设过程中不仅需要探测引起突水、突泥等低阻灾害体的物性信息，更需要获得地质灾害源的详细结构，为灾害治理提供勘探信息[2]，降低施工与灾害治理对环境的破坏。传统的隧道瞬变电磁解释方法仅给出了地下介质的电性信息，对灾害体的几何结构特征描述并不明显，因此，需要引入成像技术，提高瞬变电磁隧道超前预报方法的解释精度[3]。

由于瞬变电磁具有对低阻敏感的特征，李貅等[4]将该方法引入到隧道超前地质预报与检测领域；薛国强等[5-6]利用适合全空间模型的等效导电平面法进行瞬变电磁隧道超前预报解释，使该方法进一步推广；Sun Huaifeng 等[7]利用视电阻率定义方法实现阵列式瞬变电磁隧道超前预报解释；戚志鹏等[8]基于反函数原理实现全空间隧道瞬变电磁视电阻率解释。传统的瞬变电磁隧道超前预报方法均从扩散方程出发，根据场与电阻率的转换关系，实现地下介质的电阻率成像。扩散方程表征的是场的感应与扩散特征，主要描述物质性质的变化，对介质结构反应不敏感[9]。而地震勘探或探地雷达等满足的波动方程主要描述波在介质中的传播特征，其中波的反射与折射特征对介质几何结构反应十分敏感。因此，在波动方程条件下实现瞬变电磁解释是提高隧道超前预报解释精度的有效手段。

波场变换为瞬变电磁拟波动场成像提供了前提基础。瞬变电磁扩散场方程与波动方程存在数学变换关系[10-12]，将满足扩散方程的瞬变电磁场转换为满足波动方程的虚拟波场后，可以借助地震勘探中发展起来的一些成像方法，解决复杂情况下瞬变电磁场的成像问题[13-14]；K.H.Lee 等[10]建立了满足时域扩散方程的电磁场与虚拟波场的关系式，通过这个变换式，可以将对应地电模型的波动方程模拟结果变换成时域电磁响应，但该变换的意义并不在于对电磁场的正演模拟，而在于其逆变换过程；李貅等[15]提出了从瞬变电磁场到波场的优化算法。在波场的正变换中，在保证瞬变电磁场的计算精度的同时，应用两步最优化和正则化算法，成功地解决了波场反变换问题。戚志鹏等[16]等利用预条件正则化实现了波场的全时域变换算法。上述研究表明，变换得到的虚拟波场满足波动方程，具有传播、反射、透射特征，这为瞬变电磁场的偏移成像创造了条件。

瞬变电磁虚拟波场成像，可以借鉴地震勘探处理中比较成熟的偏移成像技术。1978 年W.A.Schneider提出Kirchhoff 积分法偏移，并得到了广泛的应用[17]。Kirchhoff 积分法偏移建立在波动方程积分解的基础上，它利用Kirchhoff 绕射积分公式把分散在地表的各个测点上来自同一绕射点的能量汇集在一起，置于地下相应的物理绕射点上，从而实现绕射点偏移成像。李貅等[18]将Kirchhoff 积分成像引入到地面瞬变电磁三维数据虚拟波场成像之中，得到了较好的应用效果。

笔者在实现瞬变电磁波场变换基础上，利用克希霍夫积分法对瞬变电磁虚拟波场进行延拓，实现瞬变电磁场的波场成像。不同于地面瞬变电磁解释方法，笔者将该方法应用于隧道超前预报二维数据偏移之中。在算法中，首先实现扩散场到虚拟波场的变换；然后忽略走向影响，基于二维克希霍夫积分实现隧道偏移成像，分别对理论模型与实测资料进行处理验证文中算法。

1 基本原理

扩散方程主要反映的是低频电磁场传播过程中的扩散和感应特征，直接利用瞬变电磁扩散场数据进行延拓成像，结果对电性界面分辨能力差，体积效应强。而波动方程反映的是波的传播特征，基于波动方程的处理方法能准确地确定介质的物性界面，给出异常体的几何信息。由于波动方程和扩散方程之间的差异，将满足扩散方程的瞬变电磁数据转换为满足波动方程的波场数据，借鉴地震勘探领域成熟技术进行电磁数据解释，是提高隧道超前预报质量的有效途径。

1.1 瞬变电磁波场变换原理

将瞬变电磁扩散场转化成虚拟波场的前提条件是瞬变电磁场与波场的各个分量具有数学上的对应关系。现以磁场的垂直分量为例，它们满足如下关系：

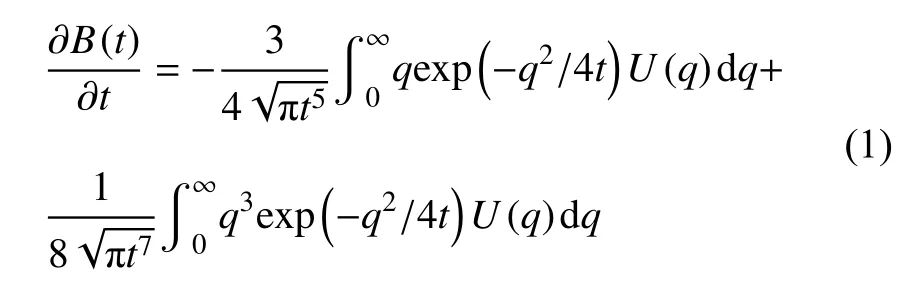
引入平滑约束，构建目标函数φ如下所示：

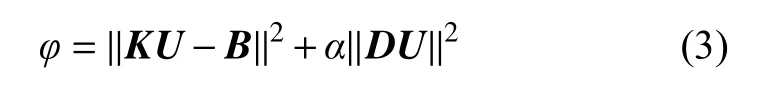
式中：‖‖2为向量的二范数；α为正则化因子；D为2 阶差分矩阵。

通过目标函数的最小化，即可获得U的近似估计，其等价方程如下式所示。

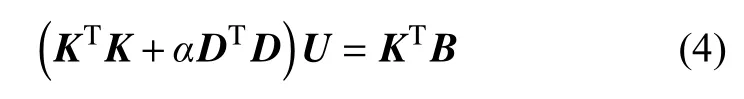
钟华森[19]、鲁凯亮[20]等给出了式(4)的波场变换算法，即设定一个时间窗口，使之在整个时间序列上滑动，每个窗口内矩阵阶数较小，可利用奇异值分解法或精细积分法进行波场变换获得波场值；在全时间段采用正则化迭代法进行波场变换；判断各窗口变换所得波场值与全时段波场值之间的相关性，若相关系数大于一定阈值，则将小时窗内波场值与全时段的变换结果进行叠加，最终得到高分辨的波场[20]。

1.2 Kirchhoff 偏移成像原理

将扩散场变换到波场后，可以利用地震波场的资料处理方法进行数据处理。通过对波场数据的处理分析，即可获得地下介质分界面的特征，进而借以研究地下地质岩层结构及其物性特征。地下介质分界面的求取问题，可以看作一种反散射问题，而地震偏移技术就是求解反散射问题、获取反射界面分布的一种技术。克希霍夫积分法是在地震资料偏移处理中应用较为广泛的一种方法，本文利用此方法进行波场数据的偏移成像。

在直角坐标系中，地下无源区波场所满足的标量波动方程为：

当对边界(图1)进行偏移时，可忽略外边界的积分，且地表与xoy平面重合时，克希霍夫解为：

图1 积分区域与边界Fig.1 Schematic diagram of regions and boundaries for integration

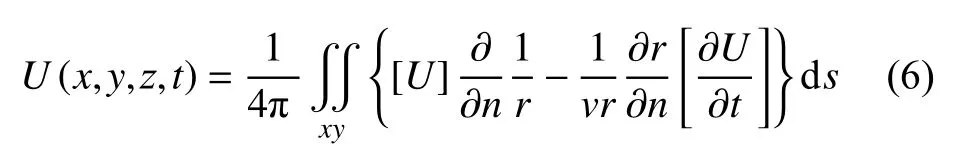
式中：[U]为波场的延迟值，A/m；r为计算点到积分扫描点的距离，m；v为虚拟波速度，s为面积，m2；n为边界的法向方向。

若已知xoy平面上波场值和波场导数值，即可利用此式计算空间中任一点处任意时刻的波场值。

在进行偏移时，测量数据定义在z=0 平面上。对于自激自收情况，二次波场产生时刻为地面接收到反射波时刻的一半，若取偏移速度为真实速度的一半，则二次场产生的时刻对应为t=0。将式(6)中的延迟式替代为超前值，即令：

式中：下标p表示偏移点p的坐标。

1.3 隧道瞬变电磁偏移成像技术

与地面瞬变电磁三维偏移不同，在进行隧道或巷道的超前预报时，经常处理来自一条测线上的数据。传统扩散场瞬变电磁不能直接对y坐标进行忽略，而是将y坐标转化成波数域进行求解；但是在波场中可以直接将y坐标忽略，从而简化数据解释。此外，克希霍夫积分的边界与区域如图2 所示，将隧道边界视为无穷远边界，并忽略无穷远边界的影响，则有二维偏移场如下式所示。

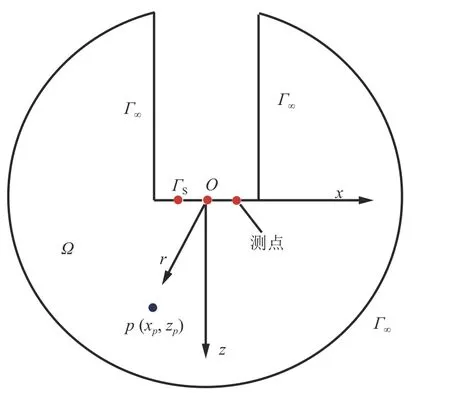
图2 隧道偏移区域与边界Fig.2 Schematic diagram of the tunnel area and boundary

在计算隧道工作面前方虚拟波场时不仅要已知地表的波场，还需已知在地下介质中虚拟波场的传播速度。根据波场变换关系可知波场的传播速度与地下介质的电阻率分布有关，如下式所示。

式中：μ为真空磁导率；H/m，σ为空间电导率，S/m。

当μ=μ0时，虚拟波场的速度只与大地介质的电导率有关，能否准确地获得地下介质的电导率，成为速度分析准确与否的关键。电阻率(电导率的倒数)是瞬变电磁解释方法的重要参数，可以根据隧道瞬变电磁电阻率成像进行虚拟波场速度提取。当获得介质电性分布后可根据具体情况采用不同的速度分析方法。原则上只要能求得准确的地层电导率，便能实现精确的速度分析，当前隧道瞬变电磁电阻率计算可以根据反函数原理进行计算[8]。

2 理论模型分析

在隧道建设过程中突水突泥灾害主要由断层、溶洞等水源灾害导致，因此，在超前预报中实现断层与溶洞的预报十分重要。为了验证文中方法，分别设计隧道低阻夹层与含水溶洞模型，采用瞬变电磁虚拟波场克希霍夫偏移算法对灾害体进行预报。

2.1 隧道充水断层模型

设计充水断层模型，如图3 所示。其中隧道宽度为12 m，背景电阻率ρ1=100 Ω·m；倾斜断层异常电阻率ρ2=1 Ω·m，宽5 m；中心点距工作面埋深为18 m，与水平线的倾斜角为75°。采用中心回线装置进行探测，发射线框3 m×3 m，发射电流1 A，点距0.5 m。

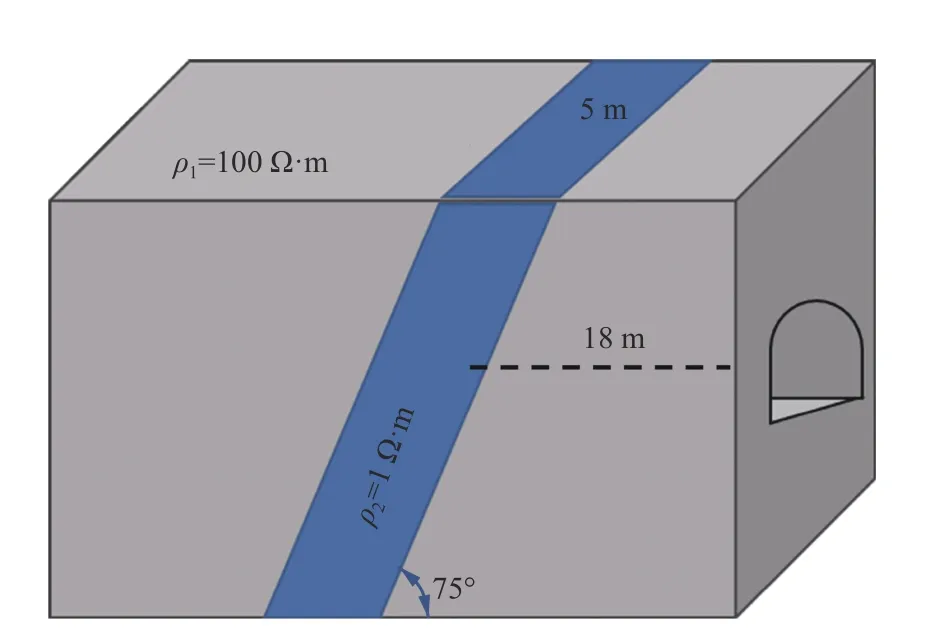
图3 充水断层模型Fig.3 Synthetic model of the water-filling fault

利用三维正演进行数值模拟，采用波场变换将衰减电压转换为虚拟波场，采用全时域视电阻率计算方法计算工作面前介质电性分布，如图4a 所示。采用本文提出的2D 克希霍夫变换方法进行偏移成像，成像结果如图4b 所示，图中同相轴与模型边界吻合且能够显示异常体的倾斜方向；视电阻率结果能够显示出低阻区域与异常倾向。将电阻率图与偏移成像结果组合，如图4c 所示，能够有效显示低阻异常边界与区域电性特征，为灾害预报与治理提供有效的几何边界信息。

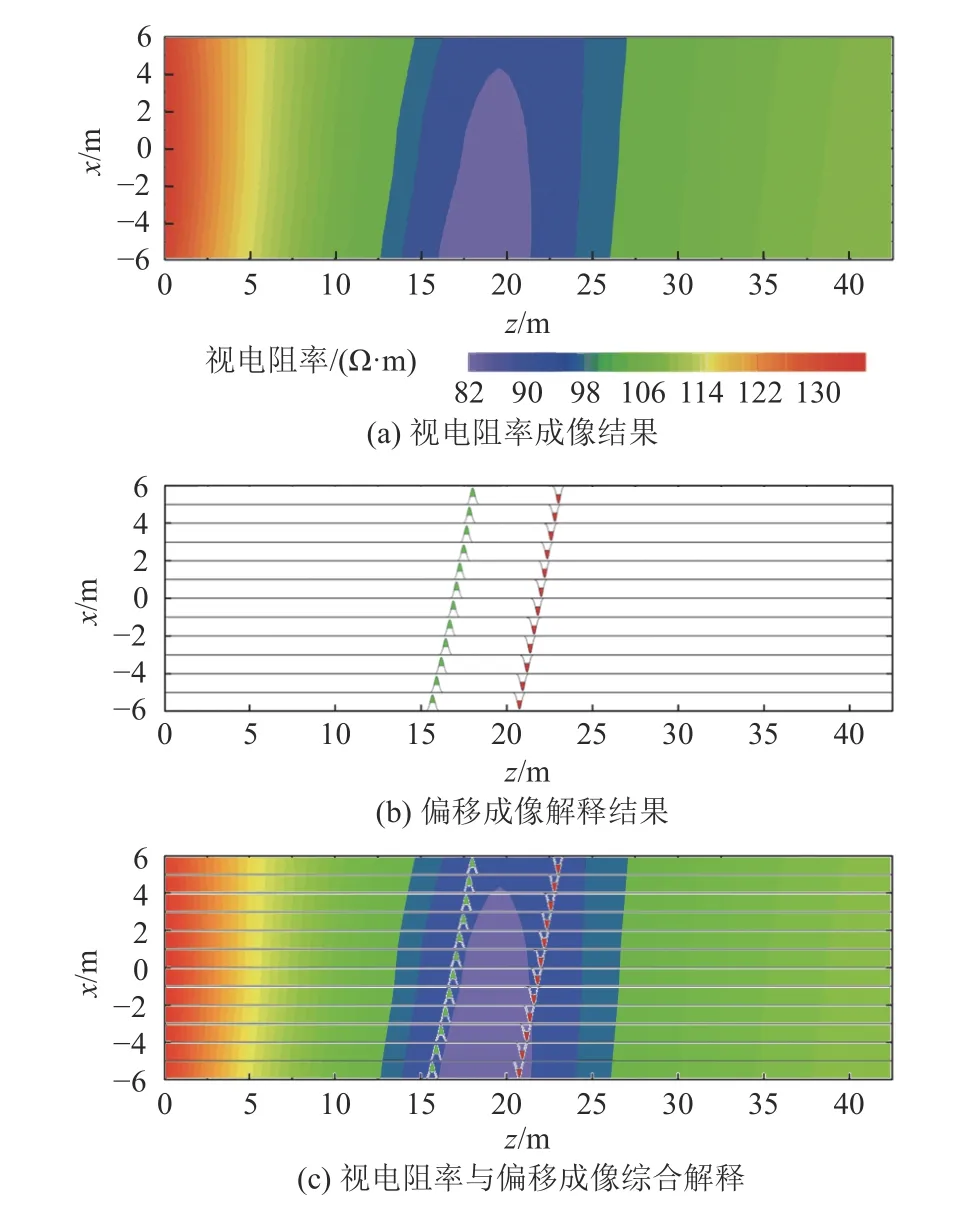
图4 隧道充水断层文中方法的综合解释Fig.4 Interpretation of tunnel water-filled fault

2.2 充水溶洞模型

隧道施工中常会遇到充水溶洞等情况，文中设计了如图5 所示的充水溶洞隧道模型，隧道宽12 m，背景电阻率为1 000 Ω·m；含水溶洞尺寸6 m ×6 m×5 m、中心点距工作面35 m、电阻率50 Ω·m。采用中心回线装置进行探测，装置参数与充水断层模型一致。

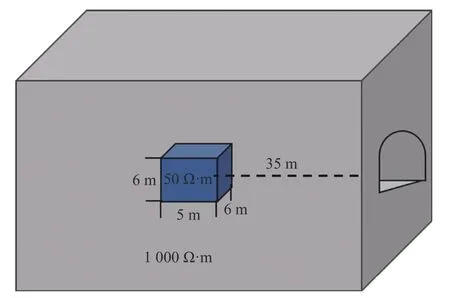
图5 充水溶洞模型Fig.5 Synthetic model of water-filling karst cave

模型中溶洞截面为矩形而电阻率断面图中则显示为类似的圆形低阻区域(图6a)，偏移成像结果(图6b)准确显示模型的边界位置。将电阻率与偏移成像二者结合(图6c)，既能解释异常的边界结构又能分辨电性分布特征。

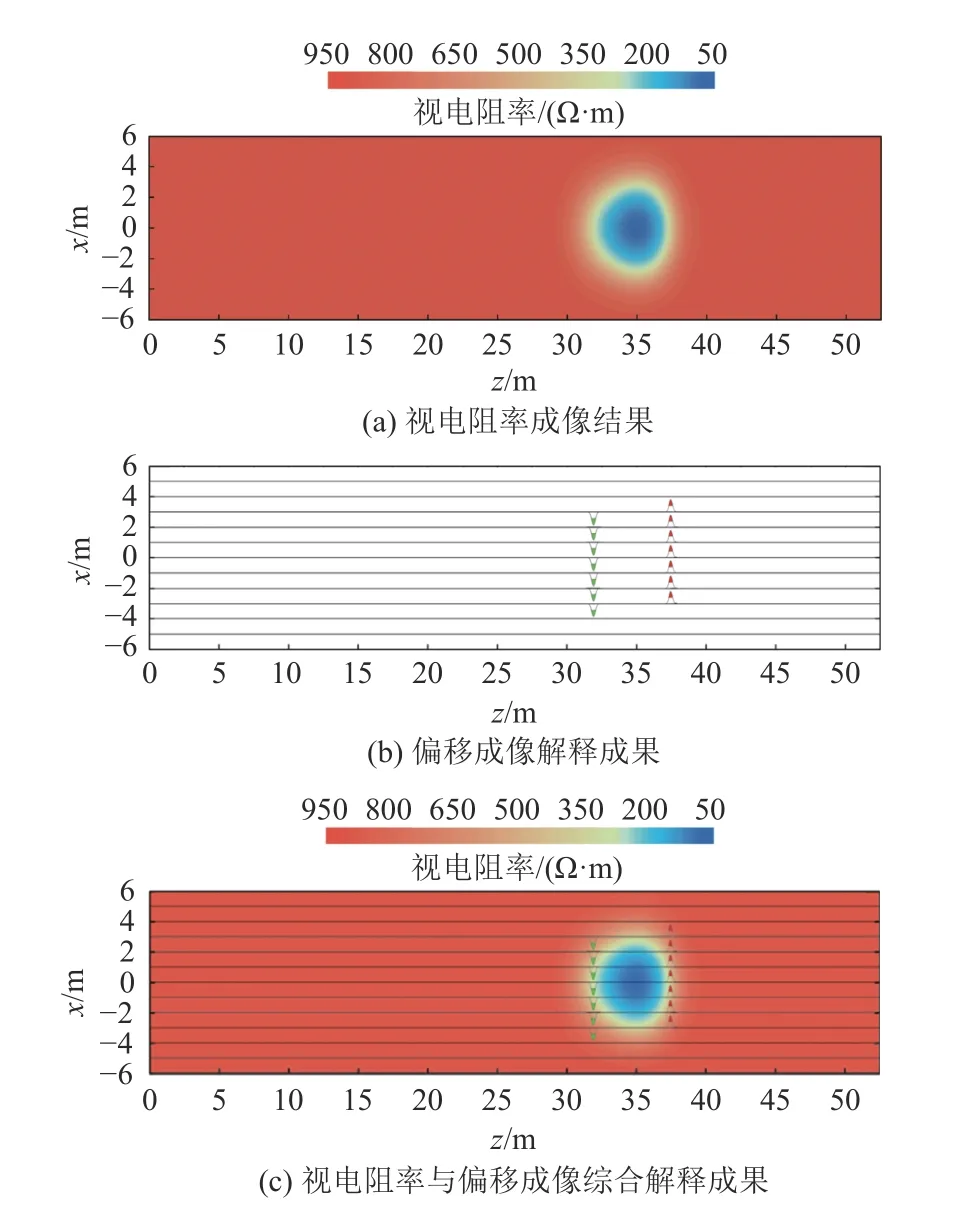
图6 充水溶洞模型本文方法的综合解释Fig.6 Interpretation of water-filled model

3 实测数据分析

以西南地区实际隧道工程为例，利用瞬变电磁进行隧道超前预报，采用虚拟波场克希霍夫偏移成像方法进行数据处理。测线位于隧道横洞内靠近出水孔一侧，采用中心回线装置进行数据采集，发射线圈边长3 m，发射频率8.3 Hz，发射电流5 A。横洞前方10 m左右有一已知出水孔且地质资料已知。为了验证方法有效性，在横洞侧壁采用中心回线装置进行测量如图7所示，引水隧洞无衬砌，且远离工作面，电磁干扰影响较小，实测数据如图8 所示。

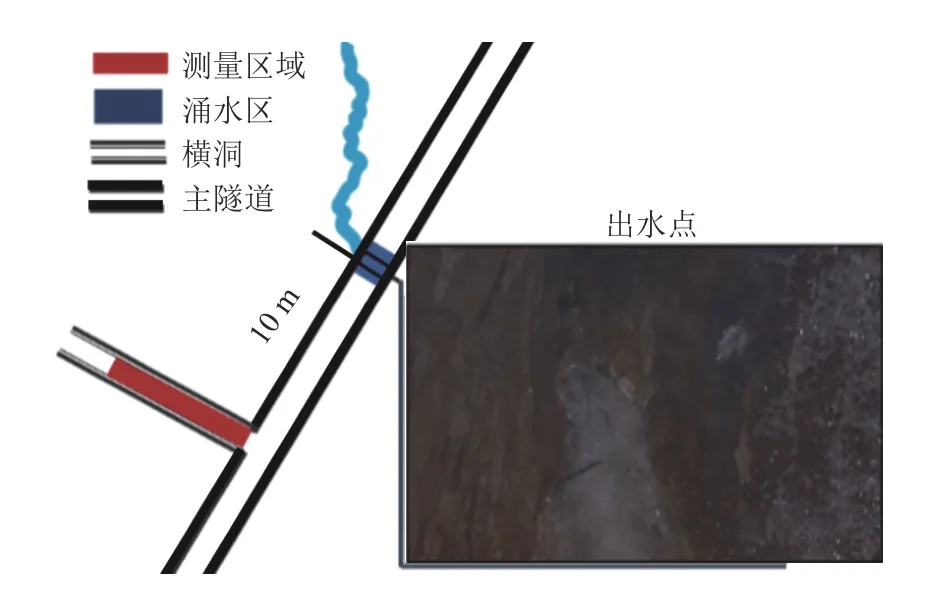
图7 横洞侧壁施工布置Fig.7 Operation layout in auxiliary tunnel sidewall

图8 测点瞬变电磁原如曲线Fig.8 Original transient electromagnetic curve of measuring point

采用文中所述的虚拟波场克希霍夫偏移方法进行数据处理，处理结果如图9 所示。由图9 可知，在深度为10 m 位置有一低电阻率薄层，根据同相轴图可知层厚较小推断为涌水裂隙。这一结果与已知出水点位置相符。在深度为10～20 m 处，电阻率介于岩石与水体之间，推断为裂隙周边受水体浸泡的岩层；在测点4−测点10、深度大于20 m 后电阻率整体较大，推断为完整的岩体。成像解释结果与实际情况一致，说明方法是稳定的，能够应用于野外数据处理。

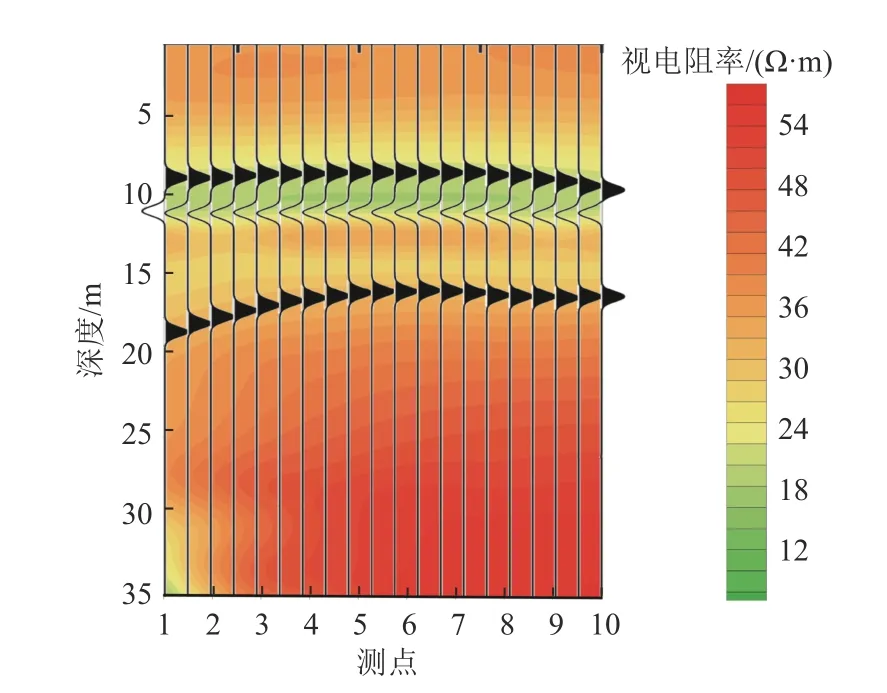
图9 实测数据及其克希霍夫偏移成像解释结果Fig.9 Kirchhoff migration imaging result of survey data

4 结 论

a.瞬变电磁场经积分逆变换后可转换为满足波动方程的虚拟波场。利用克希霍夫积分方法可将虚拟波场从地面向地下进行逆时偏移，得到清晰的异常边界。将得到电阻率的断面分布与偏移成像结果进行综合实现联合反演解释。

b.在扩散场瞬变电磁解释中，对于二维地电断面情况需要将走向方向转化为波数域，增加了数据解释的难度，而转化成虚拟波场后二维解释可将走线方向坐标直接忽略，不仅降低了二维数据解释难度，而且获得了准确的剖面构造特征。

c.将虚拟波场克希霍夫二维偏移成像方法应用于理论模型数据处理，综合解释结果与理论模型相符，不仅能够判断异常电阻率分布区域，同时能够揭示灾害体的倾向、电性边界等构造特征，充分验证了方法的正确性。将方法应用于实际资料处理，综合解释结果圈定了低阻异常位置，波场成像有效显示导水通道的边界与走向特征，解释结构与隧道开挖揭露结果一致。理论结果与实测数据处理结果表明瞬变电磁虚拟波场克希霍夫偏移成像可以实现隧道超前预报，能够为地质灾害预警与防治提供丰富的灾害体地质信息。