煤矿水平孔复杂地质模型方位电磁波响应数值模拟

张 意，康正明，冯 宏，韩 雪，陈 刚

(1.煤炭科学研究总院，北京 100013；2.中煤科工集团西安研究院有限公司，陕西 西安 710077；3.西安石油大学 电子工程学院，陕西 西安 710065；4.中国石油集团测井有限公司，陕西 西安 710077)

我国煤炭开采已逐步普及自动化并进入智能化发展阶段[1]，煤岩界面识别是实现煤矿巷道自动化掘进和煤矿智能化的关键技术之一[2-4]。现有测井岩性界面识别技术中，方位电磁波测井因探测范围较大(根据所使用源距和频率的不同，商用仪器的探测深度及探边距离可达几米至几十米)，能够分辨煤岩界面方位，可探测低阻异常体等优势，其理论发展和技术进步对煤矿智能化发展具有重要意义[5-7]。

传统电磁波测井仪采用轴向发射和轴向接收线圈，能够适用于随钻测量环境，但只能测量地层电阻率，无法测量岩性界面信息[8-10]。随着水平井钻井技术的发展，随钻地质导向需要一种能够识别地层界面的方法，从而使方位电磁波测井仪器得到发展，其采用轴向线圈和倾斜/水平线圈相结合的组合方式，能够同时测量电导率和岩性界面信息[11-14]。现有商业方位电磁波测井仪器针对油田测量环境设计，而油田测量环境和煤田测量环境具有较大不同：①油田测井目标地层的电阻率较低(小于100 Ω·m)，而煤层的电阻率值范围较大(20～10 000 Ω·m)，已发表论文中对高阻情况的讨论较少；② 相对于油田测井，煤田常用的钻杆尺寸较小，电阻率各向异性处在高电阻率范围，煤田测量情况下仪器、地层参数变化对方位电磁波探测特性的影响尚不明确；③煤田测量仪器存在本质安全要求，仪器设计和制造需要满足煤矿测量的安全要求；④ 相对于油田测井，煤田测井对电阻率值的准确测量要求不高，但对煤岩界面位置的测量精度要求较高。

已发表的论文中针对煤田测井的方位电磁波测井研究较少，主要研究有：顺煤层钻进随钻方位电磁波顶底板探测影响因素[15]；电导率、介电常数与发射频率的关系，以及煤矸石、源距、频率等对方位电磁波测量响应的影响[16-17]；水平孔煤岩界面方位电磁波测井仪器探测性能[18]。上述研究主要采用的是水平层状地层模型，复杂3D 地质模型中的钻孔、采空区、起伏地层响应尚不明确，本文针对3～6 m 厚的煤层，采用3D 有限元数值模拟方法，建立钻孔、采空区、起伏地层3 种典型地质模型，研究不同源距和发射频率情况下的钻孔、采空区、地层起伏等环境参数变化对方位电磁波测量响应的影响。

1 仪器参数及基本原理

1.1 正演模拟仪器参数

目前没有针对煤矿测量环境的商用方位电磁波测井仪器，为分析方位电磁波测井在煤矿复杂3D 地质模型中的响应特征，使用较成熟的油田方位电磁波测井PeriScope 仪器参数进行有限元正演模拟，以分析其对复杂3D 地质模型的探测效果。PeriScope 仪器线圈系中，倾斜线圈既能探测径向分量又能探测轴向分量，本文主要研究倾斜线圈对煤岩边界的探测能力。如图1 所示，PeriScope 仪器倾斜线圈系采用4 种工作源距L：0.558 8、0.863 6、2.133 6、2.438 4 m，用于探测岩性边界的地质信号采用3 种发射频率：0.1、0.4、2.0 MHz(下文也称其为低频、中频、高频)。

图1 PeriScope 方位电磁波测井仪结构Fig.1 Structure of PeriScope azimuth electsromagnetic wave logging tool

1.2 基本原理

当采用时谐源exp(−jωt)时，电磁波测井电磁场满足微分Maxwell 方程组[19-20]：

式中：H为磁场强度矢量，A/m；E为电场强度矢量，V/m；JS为外加电流密度矢量，A/m2；ω为角频率，rad/s；σ为电导率，S/m；ε为介电常数，F/m；μ为磁导率，H/m；j 为虚数单位。

将式(2)两端求旋度并代入式(1)中可得：

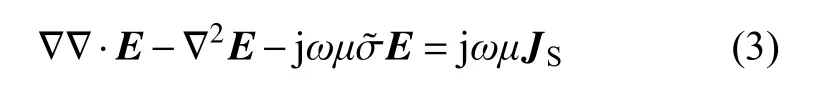
利用变分原理和泛函分析，可得电场强度矢量E的泛函表达式[21]：

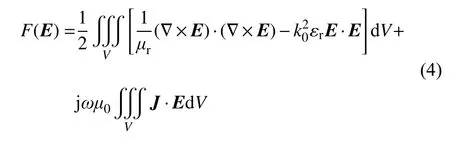
式中：F(E)为电场强度矢量E的泛函；μr为相对磁导率；μ0为真空中磁导率，μ0=4π×10−7H/m；；εr为相对介电常数；k0为自由空间波数，rad/m；V为体单元。

将求解域离散成若干个子空间，在子空间坐标系下，对每个单元利用形状函数导出场量求解表达式，并扩展到总矩阵方程：

式中：A为总刚度矩阵；X为未知量；b为施加条件。通过求解式(5)可得到整个求解域电磁场分布。

对电场强度进行线积分可得到不同方位的电压信号。倾斜线圈地质信号计算常用的一种方法是，测量倾斜线圈在仪器沿轴线旋转到不同方位角α1和α2(α1和α2常取0°和180°)时的接收电动势，将其转化为幅度比和相位差地质信号：

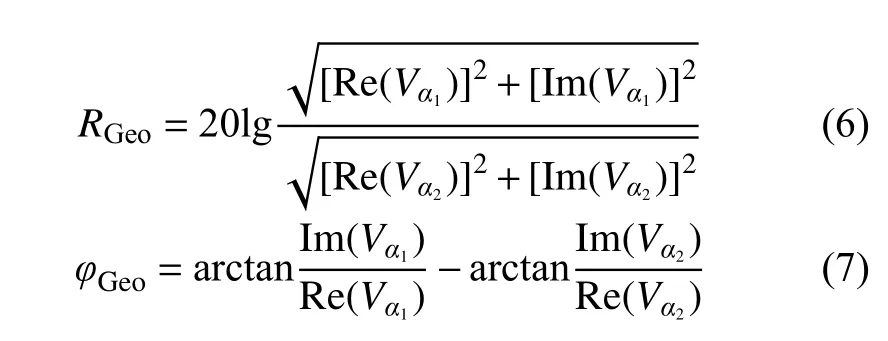
式中：RGeo为幅度比地质信号，dB；φGeo为相位差地质信号，(°)；Vα1为接收在角度1 时的测量电压，V；Vα2为接收在角度2 时的测量电压，V。Re表示取电压的实部信号，V；Im表示取电压的虚部信号，V。

2 钻孔的影响

煤矿钻井不仅使用泥浆钻进的方式，也使用风钻等钻进方式，工作面探放水孔或瓦斯抽采孔在完钻后通常保持裸眼状态，孔中介质除泥浆外还存在空气或地层水的情况。钻孔半径、孔中介质与孔壁地层的岩性分界面都对测量响应有一定影响，为研究方位电磁波测井响应受煤矿钻孔的影响，建立如图2 所示的三层水平分层地层模型，其中X轴为水平方向(X轴位于煤层中心)，Z轴为竖直方向，Y轴垂直纸面向里，H为煤层厚度，ρC为煤层电阻率，ρU为顶板电阻率，ρD为底板电阻率，rT为仪器半径，rB为钻孔半径，d为偏心距，ρm为钻孔中介质电阻率。另外，f为发射频率。

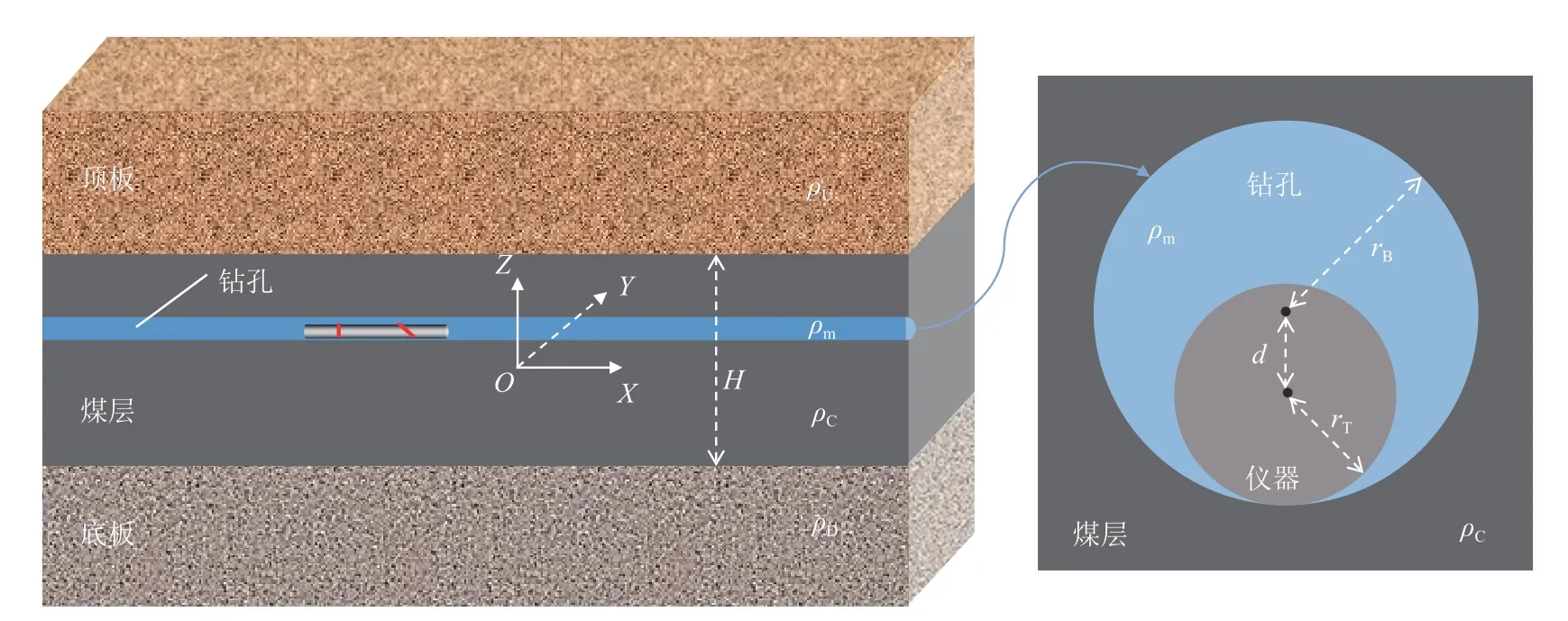
图2 钻孔地质模型及钻孔横截面示意Fig.2 Borehole geological model and borehole cross section

2.1 钻孔介质

在仪器居中时，为计算煤田常用钻杆直径和孔径参数下方位电磁波测井测量响应特征，在如图2 所示的模型中设置模型参数：H=5 m，ρC=200 Ω·m，ρU=10 Ω·m，ρD=10 Ω·m，rT=3.65 cm(直径73 mm 的钻杆在煤矿井下钻井作业中较为常用)，rB=5 cm，d=0 m(仪器居中)，ρm=0.1(盐水)、10(淡水)、107(空气) Ω·m，f=0.4 MHz。仪器保持水平且仪器中心处于相同的X位置，钻孔在不同深度位置的方位电磁波测量结果如图3 所示(相当于在不同Z深度位置分别打水平孔，每个钻孔只测量一个相同X位置的点)，可以看出当仪器居中时，相同源距下，模型中不含钻孔、模型含充水钻孔、模型含充空气钻孔的方位电磁波测量曲线差异可以忽略不计，也即仪器居中时钻孔流体对方位电磁波的影响较小，在实际测量时应尽可能让仪器保持居中状态，也即仪器居中测量时无需进行井眼影响校正。

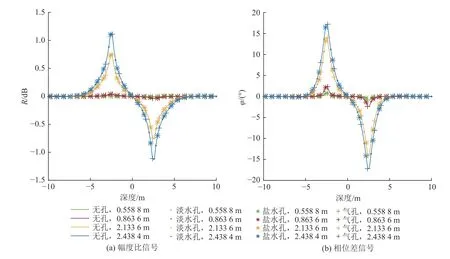
图3 钻孔介质影响对比Fig.3 Comparison of the influence of media in drilling hole

2.2 偏心距

为计算不同偏心距对方位电磁波测量响应的影响，在含钻孔的均质模型中设置模型参数：H=100 m，ρC=200 Ω·m，ρU=200 Ω·m，ρD=200 Ω·m，rT=3.65 cm，rB=7.5 cm，d=0～3.85 cm，ρm=0.1、10.0 Ω·m，f=0.1、0.4、2.0 MHz。不同发射频率时的方位电磁波测量响应如图4 所示，可以看出，当钻孔中为淡水时，模型设置的偏心距对幅度比和相位差影响较小，可以忽略不计。当钻孔中为盐水时，幅度比信号受偏心距的影响较小，相位差受偏心距的影响较大；随偏心距增加，钻孔水对方位电磁波地质信号的影响增大，且随频率的增加，其对地质信号的影响也增大；对于地质信号的常用阈值(幅度比信号0.25 dB，相位差信号1.5°)，在钻孔半径为7.5 cm，钻孔偏心距大于1 cm 时，0.558 8 m 和0.863 6 m 源距在2 MHz 频率时的相位差信号需要做偏心影响校正或在测量时为仪器添加扶正器，其他源距和发射频率下，偏心距的影响较小。

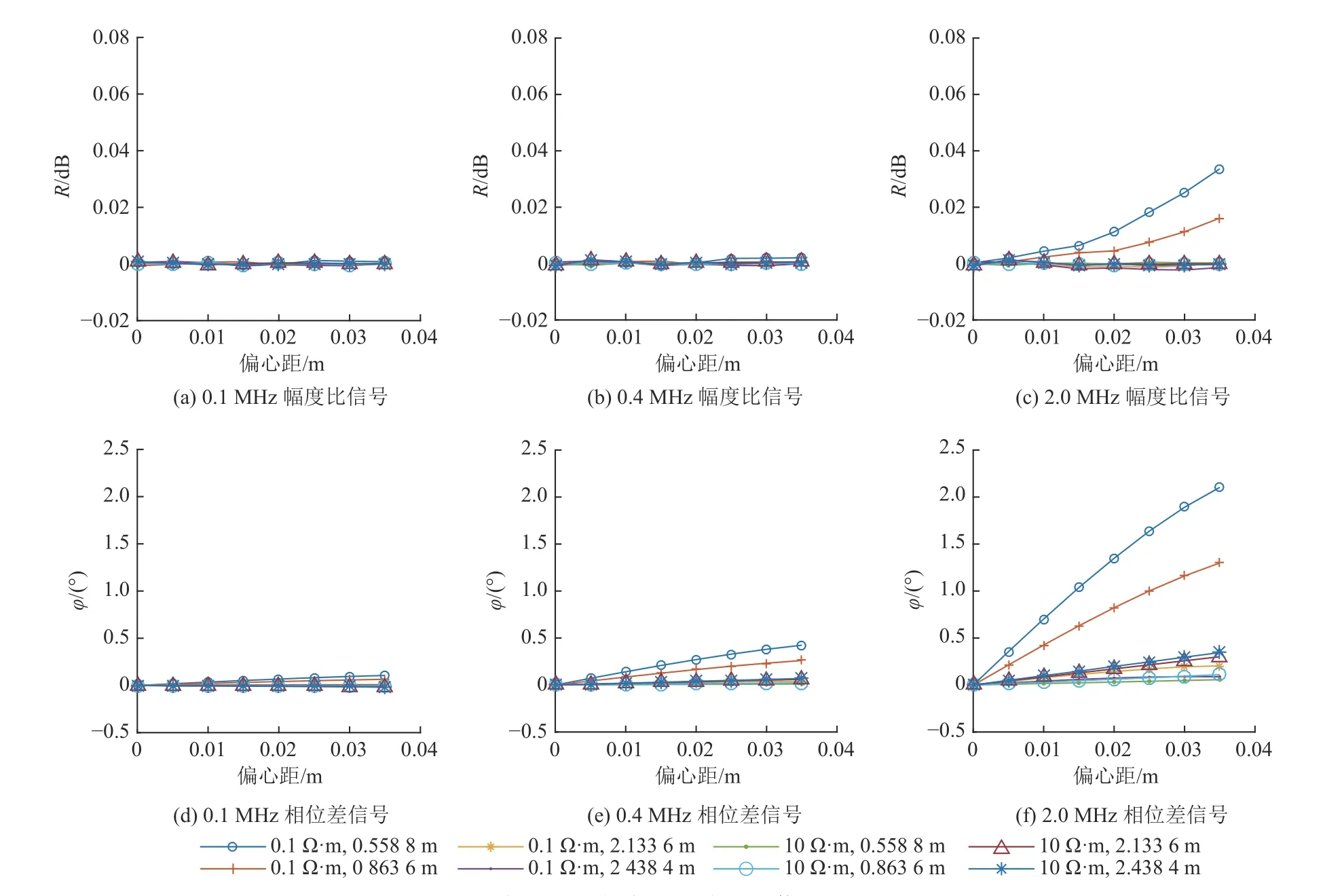
图4 偏心距对方位电磁波测量信号的影响Fig.4 Influence of eccentricity on electromagnetic wave measurement signal

2.3 钻孔半径

在含钻孔的均质模型中，为计算仪器始终位于钻孔底部时钻孔流体对测量响应的影响，设置模型参数：H=100 m，ρC=200 Ω·m，ρU=200 Ω·m，ρD=200 Ω·m，rT=3.65 cm，rB=4～20 cm，d=rB−rT(仪器始终位于钻孔底部)，ρm=0.1(水)、107(空 气) Ω·m，f=0.1、0.4、2.0 MHz，仪器保持水平，不同井眼半径时的方位电磁波测量结果如图5 所示，可以看出，当钻孔中为空气时，幅度比信号受钻孔直径的影响可以忽略不计，当发射频率为2 MHz、源距为0.558 8 m 和0.863 6 m 时，相位差信号受钻孔直径影响较大；随钻孔半径的扩大，方位电磁波受钻孔影响增大，幅度比在钻孔直径小于14 cm 时受钻孔影响较小，无需做钻孔影响校正，相位差在钻孔直径超过一定值(0.4 MHz 时钻孔半径超过6 cm，2.0 MHz 时钻孔半径超过4.5 cm)后需要做钻孔影响校正；在模型设置的钻孔半径范围内，源距越小，受钻孔影响越大。

图5 仪器位于钻孔底部时钻孔半径的影响Fig.5 Influence of borehole radius when instrument is located at bottom of the well hole

3 起伏地层

为了方便计算方位电磁波对煤层边界的响应特性，在理论研究时往往忽略了地层的起伏形态，导致理论计算模型与实际地层模型存在一定的差异，因此，有必要建立起伏地层边界，考察其形态特征对探边特性的影响程度。建立如图6 所示的地层模型，其中X轴为水平方向(X轴位于起伏地层ZS=0 的位置)，Z轴为竖直方向(Z 轴穿过起伏地层幅度最高值点)，Y轴垂直纸面向里，ρC为煤层电阻率，ρD为底板电阻率，D为仪器中心距X轴距离，A为地层起伏的幅度，T为地层起伏周期，f为发射频率。地层起伏界面公式由下式产生：

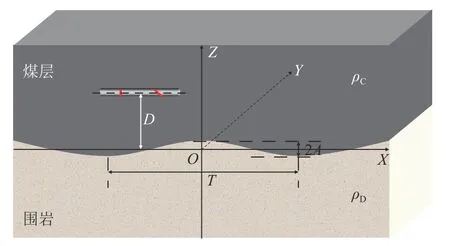
图6 起伏地层模型Fig.6 Undulating formation model

式中：ZS为起伏地层界面与XZ平面交线。

3.1 地层界面起伏幅度响应

在如图6 所示的起伏地层模型中，设置参数：ρC=200 Ω·m，ρD=10 Ω·m，D=1 m，A=0.05、0.25、0.50 m，T=50 m，f=0.4 MHz。仪器沿X 轴方向移动的测量响应如图7 所示，可知地层界面与仪器相对夹角在仪器横向移动时虽不断变化，但方位电磁波测量响应信号仍能反映地层的起伏变化，0.558 8 m 和0.863 6 m 信号探边距离较小，在常用阈值情况下，无法探测距离界面中心距离1 m 的地层起伏变化(其探边距离小于1 m)，2.133 6 m 和2.438 4 m 源距的线圈系探边距离大于1 m。2.133 6 m 和2.438 4 m 信号对地层起伏幅度为A=0.05 m 的地层(地层总起伏0.1 m)，其响应信号的变化在10%左右(测量响应变化常用阈值也为10%)，地层0.1 m 的起伏是该正演条件下仪器测量信号能够分辨的最小值。

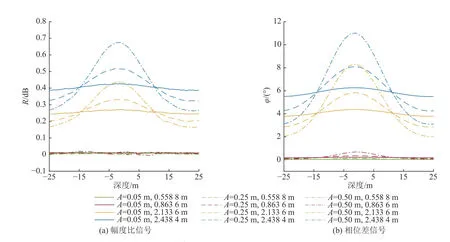
图7 起伏地层幅度影响Fig.7 Influence of undulating formation amplitude

3.2 起伏地层幅度探测能力分析

在如图6 所示的起伏地层模型中，设置参数：ρC=200 Ω·m，ρD=10 Ω·m，D=2、3 m，A=0.05 m，T=50 m，f=0.4 MHz。其模拟结果如图8 所示，可知在地层起伏变化较小时(起伏0.1 m)，使用幅度阈值0.25 dB和相位差阈值1.5°，在仪器与X轴距离D=2 m 时，0.4 MHz 发射频率的幅度比响应信号小于0.25 dB，无法反映界面幅度变化，但2.438 4 m 源距相位差信号响应值大于1.5°，其探边距离大于2 m，能够反映界面起伏变化。在0.4 MHz 发射频率、仪器与X轴距离D=3 m 时，各源距的幅度比和相位差信号都无法反映界面的起伏变化。

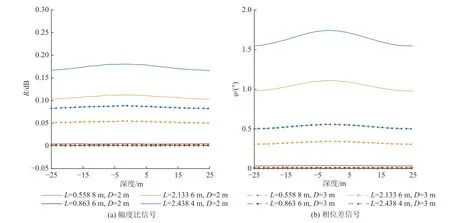
图8 仪器与地层界面距离的影响Fig.8 Influence of distance between instrument and formation interface

3.3 仪器穿过起伏地层界面响应

在如图6 所示的起伏地层模型中，设置参数：ρC=200 Ω·m，ρD=10 Ω·m，D=0 m，A=0.5 m，T=50 m，f=0.4 MHz。正演模拟结果如图9 所示，幅度比和相位差信号在穿过界面时出现极大值，0.558 8 m 和0.863 6 m源距的幅度比信号对模型设置的界面响应值较小，无法反映界面变化，但2.133 6 m 和2.438 4 m 源距测量响应大于阈值，能够反映界面变化；相位信号所有源距都对界面变化有所响应，可知相位差信号的适应范围较幅度比信号广。

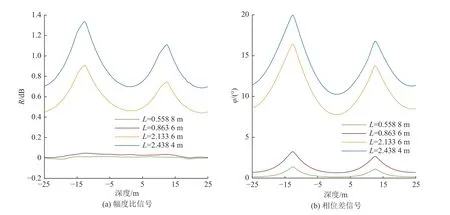
图9 仪器穿过起伏地层界面响应Fig.9 Instrument response through an undulating formation interface

4 采空区

为研究方位电磁波对采空区的探测性能，建立如图10 所示的采空区地质模型，其中采空区为长方体形状，ρC为煤层电阻率，ρG为采空区电阻率，LG=10 m、W=4 m、HG=4 m 分别为采空区的长、宽和高。

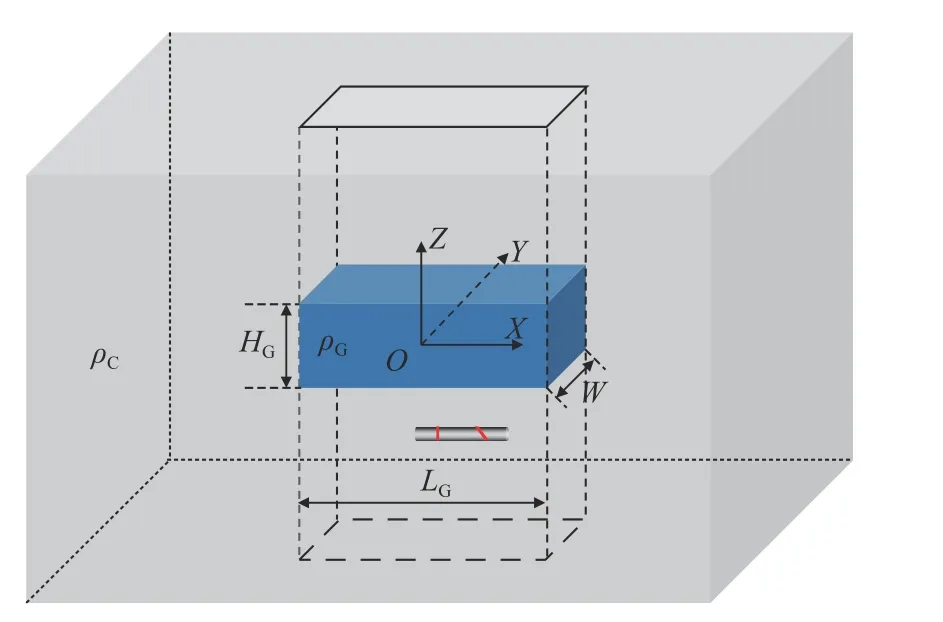
图10 采空区地质模型Fig.10 Geological model of goaf

4.1 仪器穿过采空区响应对比

设置地层模型参数为：ρC=200 Ω·m，ρG=0.1、1、1 000 Ω·m，f=0.1、0.4、2.0 MHz。模拟计算时仪器保持水平沿Z 方向移动的测量曲线如图11−图13 所示。

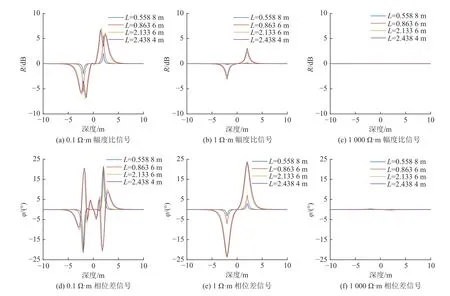
图11 频率0.1 MHz 时仪器纵向移动采空区测量响应对比Fig.11 Comparison of measement response of instrument moving longitudinally in goaf at the frequency of 0.1 MHz

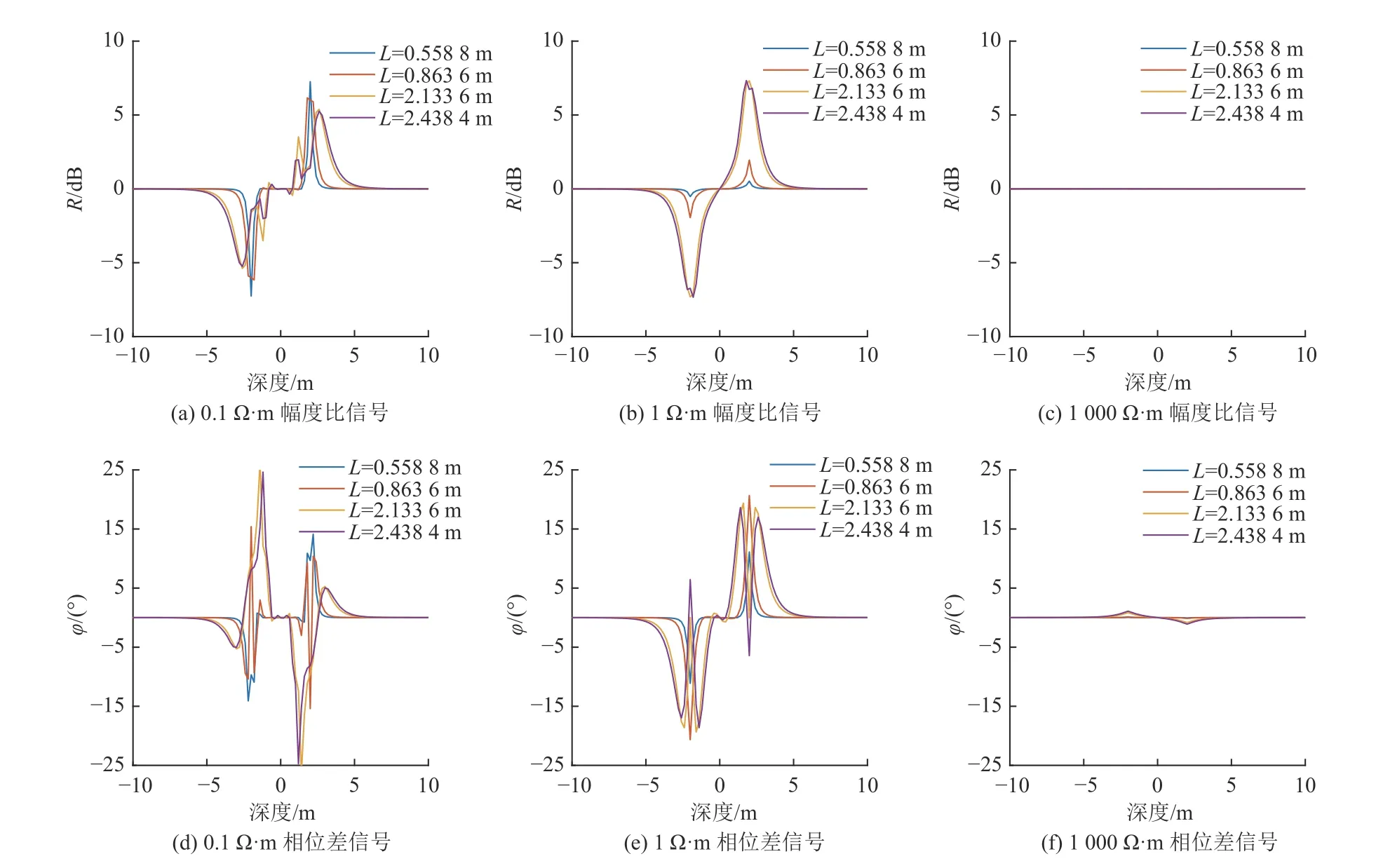
图12 频率0.4 MHz 时仪器纵向移动采空区测量响应对比Fig.12 Comparison of measurement response of instrument moving longitudinally in goaf at the frequency of 0.4 MHz

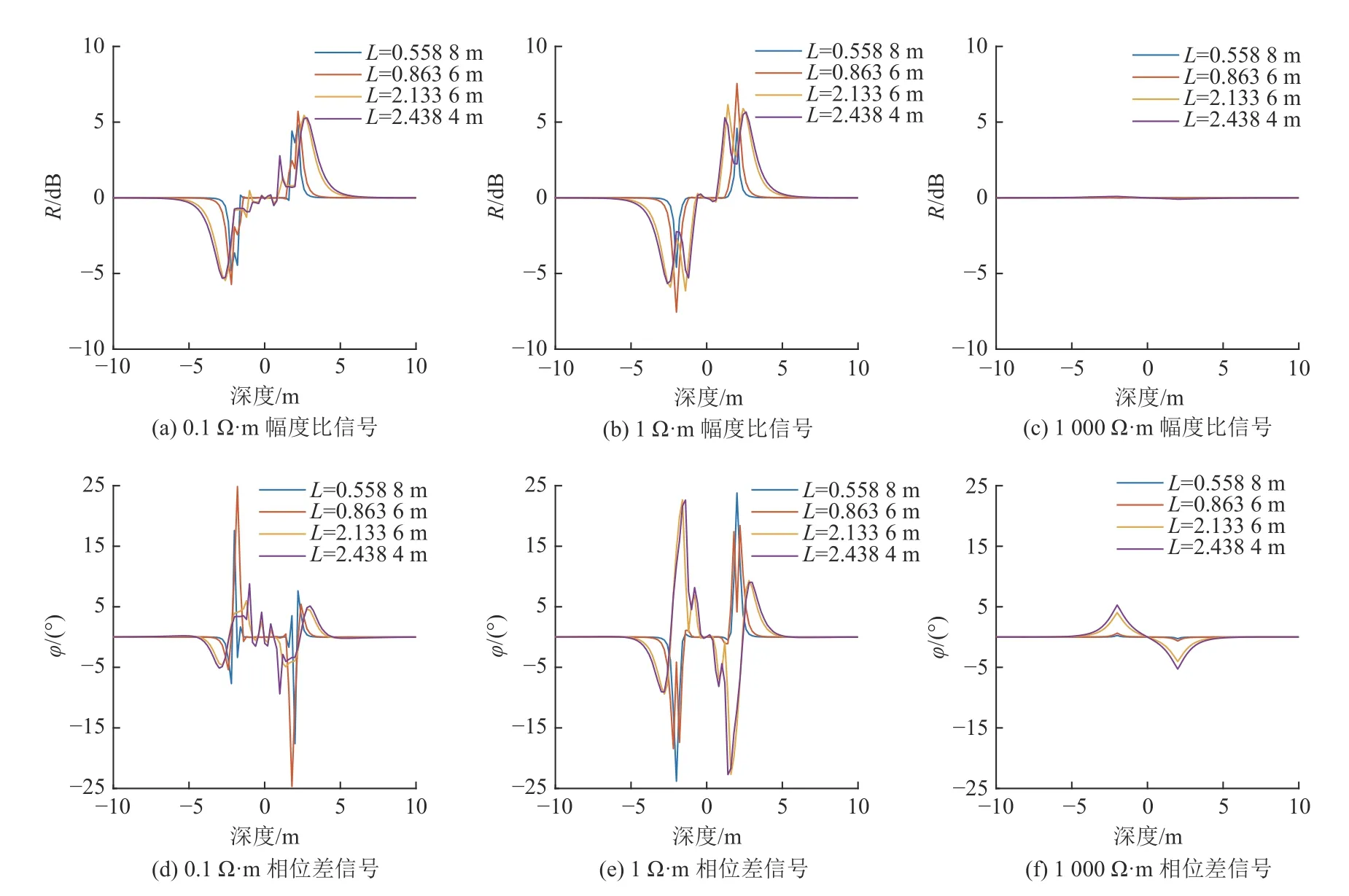
图13 频率2.0 MHz 时仪器纵向移动采空区测量响应对比Fig.13 Comparison of measement response of instrument moving longitudinally in goaf at the frequency of 2.0 MHz

可以看出：

(1) 在采空区电阻率为0.1 Ω·m 时，幅度比和相位差响应信号在界面处出现了震荡，且频率越高、源距越大震荡越强，低频、短源距组合较适合测量低阻采空区，高频、长源距虽能对低阻采空区进行测量，但其定量解释存在一定困难；

(2) 在采空区电阻率为1 Ω·m 时，发射频率为0.1 MHz 时，各源距的幅度比和相位差在岩性边界处的信号较为理想(如图10a、图10e)；随着频率的增加，2.133 6 m 和2.438 4 m 源距的幅度比和相位差曲线开始出现震荡，因此，长源距适合在低频时进行测量；

(3) 在采空区电阻率为1 000 Ω·m 时，幅度比和相位差对岩性边界不敏感，其在0.1 MHz 和0.4 MHz 发射频率的测量响应值均低于幅度比0.25 dB、相位差1.5°的阈值，相位差响应信号对高阻岩性界面的敏感度高于幅度比信号。随频率的增加，方位电磁波响应信号幅值增大，相位差在2 MHz 发射频率时能够测量高阻边界，对高阻边界的探测可用幅度比和相位差联合分析。

综上所述，方位电磁波不同源距、频率的测量信号，对采空区电阻率的适用范围不同，低发射频率和短源距适合探测低阻采空区，高频长源距适合探测高阻采空区。

4.2 仪器未穿过采空区响应

设置地层模型参数为：ρC=200 Ω·m，ρG=0.1、1、1 000 Ω·m，f=0.4 MHz。仪器纵向深度为Z=3 m，模拟计算时仪器保持水平沿X方向移动，测量曲线如图14 所示，当采空区电阻率为0.1 Ω·m 和1 Ω·m 时，幅度比和相位差信号均有响应，幅度比信号随采空区电阻率的减小而增加，但相位差信号在采空区电阻率为0.1 Ω·m 时的响应值小于在1 Ω·m 时，可知幅度比信号对低阻异常体更敏感；在采空区电阻率为1 000 Ω·m时，幅度比和相位差信号均较小，无法反映高阻采空区岩性界面。

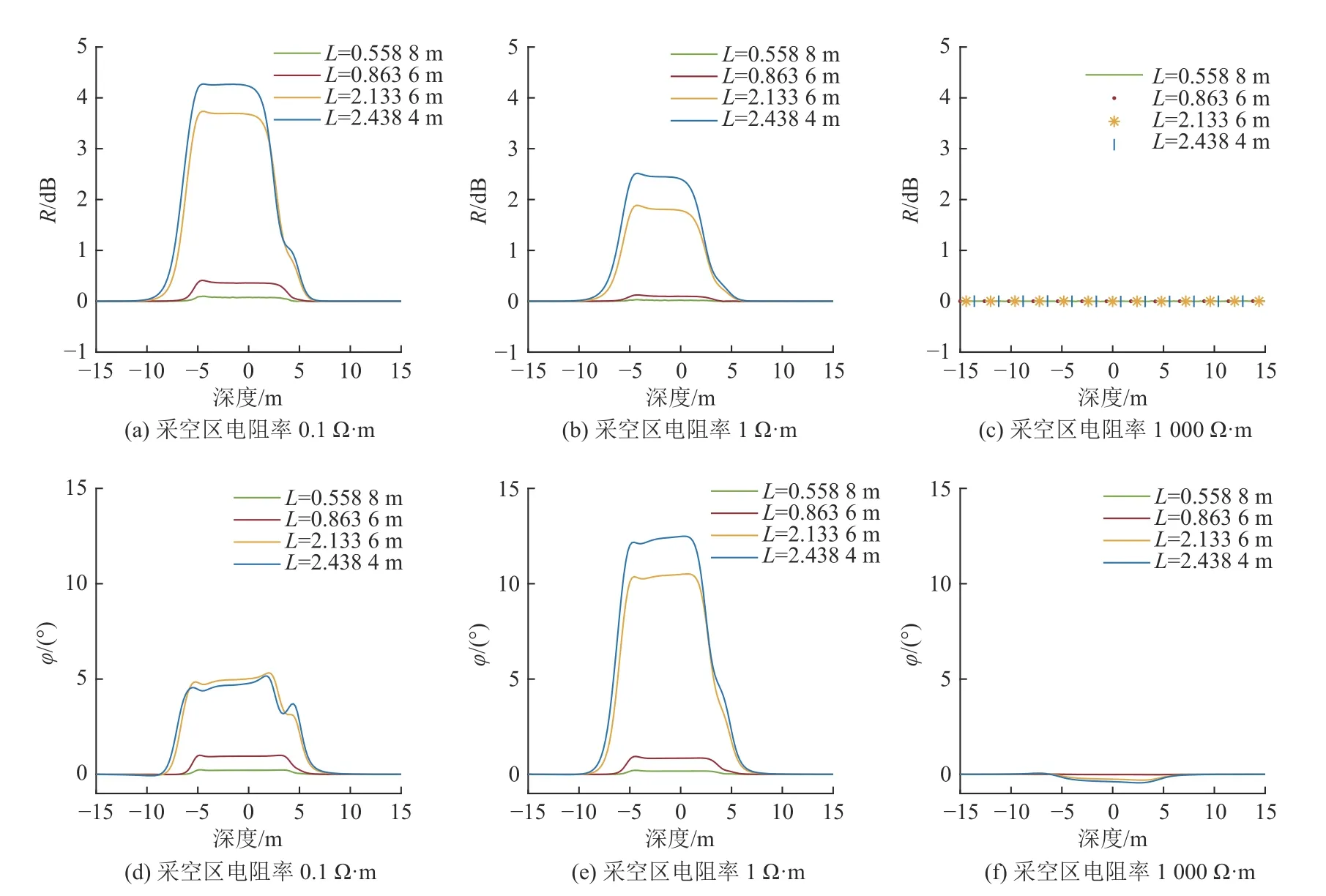
图14 频率0.4 MHz 时仪器横向移动采空区测量响应对比Fig.14 Comparison of measurement response of instrument moving laterally in goaf at the frequency of 0.4 MHz

5 结 论

a.对煤矿井下常见的干孔测量工况，钻孔流体对方位电磁波测量响应的影响较小，可以忽略不计；当钻孔中为低阻水时：在直径100 mm 的孔中，73 mm 直径的方位电磁波仪器在居中时受钻孔流体的影响可以忽略；钻孔对方位电磁波测量响应的影响随偏心距的增加而增加，仪器偏心时在钻孔直径大于9 cm 时需要对地质信号进行钻孔影响校正。

b.在本文模拟的模型条件下，方位电磁波能够反映10 cm 的地层起伏变化，长源距的信号对地层起伏敏感度要高于短源距信号。

c.方位电磁波地质信号对低阻采空区较为敏感，但不同源距和发射频率的电阻率适用范围不同，应用时需根据电阻率测量值选取相应频率和源距的数据进行解释；当采空区为高阻时，需要采用高发射频率(如2.0 MHz)下的相位差信号进行探测。