思维进阶：让简单的知识不简单

施丽

【摘要】本文从运算律的课例中拓宽教师的教学思路，深度研究“交换律”的内容，是建立在学生已经经历“观察—猜想—验证—归纳”的探究过程上，大胆鼓励学生在课堂上继续理性地探新奇、辨真伪、明所以然，自然推导至其他运算中交换律的问题，着眼于换个角度，生成不简单的精彩课堂.

【关键词】交换律;不简单;探究;教学

一、课例描述

前不久，学校的青年教师进行了一次“同课异构”的数学课堂教学展示.教学内容是苏教版小学数学四年级下册“运算律”.听了几节课，笔者发现教师们基本上都是按照这样的教学思路实施教学的，具体表现在以下七个方面.

1.“朝三暮四”创设情境或开门见山.

2.说一说：这两个算式里的加数分别表示什么？结果相等可以用等号连接.

3.同学们能再举几个这样的例子吗？

4.仔细观察这些算式，同学们有什么发现？（揭示加法交换律）

5.用自己喜欢的方式表示加法交换律.

6.经历了“观察—猜想—验证—归纳”的探究过程后，同学们放手研究加法结合律.

7.练习巩固，回顾反思.

每位教师在课堂中不仅重视学生主体地位的体现，而且重视对学习方法的渗透，让学生充分经历观察—猜想—验证—归纳的探究过程，多感官地理解加法交换律和结合律的含义.然而，在某节课的结尾谈收获的环节中，一名学生坚定地说道：“除了加法有交换律外，乘法也有交换律，而减法和除法没有交换律！”教师立即询问那名学生：“你怎么知道的啊？！”这名学生骄傲地说：“这个很简单呀！”其他学生诧异地看着教师，教师提议给出掌声.

二、引发思考

连续听课后，最让笔者感受深刻的不是教师在新授部分做到“朴实无华，彰显魅力”，也不是教师在练习部分做到“层次分明，循序渐进”，而是学生口中的“简单”一词.如果从师、生双重角度上看，“简单”在于以下两个方面.

（一）教学知识中的“简单”

追溯学生的认识过程，其实从一年级开始，他们就对加法交换律有了初步的感知;他们在二年级认识了乘法口诀表，对乘法交换律有了初步的感知;到了三年级，他们已经会用交换两个加数（乘数）的位置进行验算或简便计算.此时，加法（乘法）交换律已经被当成一种潜意识的规定，被学生默认运用.此时，学生如果真正地学起来，自然就会认为“简单”，而教师难免会觉得知识点太简单，学生的探究性不强.

（二）教学现场中的“简单”

教师将掌声送给了那句“这个很简单呀”，这样的处理无疑是让其他学生带着疑惑走出课堂，而且失去了学生思维进阶的契机，这样的课堂才是简单的.“为什么加法和乘法有交换律，而减法和除法没有交换律呢？”对于这一问题，数学教材里的运算律并没有涉及减法和除法，那么是否就不需要建构呢？如何将“简单”的知识变得“不简单”，如果由我来实施教学，那么学生的思维又该如何进阶呢？

三、我的教学课堂

片段一：多元表征 让知识形成过程“看得见”

（教学加法交换律之后）师：关于加法交换律，你们有什么想说的？

生1：我知道两个数相加，交换两个加数的位置，和不变.

生2：我知道加法交换律可以用字母a+b=b+a表示.

师：我们今天继续研究交换律.（板书：交换律）

教师出示研究一：新新在学习的过程中发现3×5=5×3，他认为乘法也有交换律，你们能试着举出几个这样的例子并选择其中的一个，用画图或自己喜欢的方式解释说明一下吗？

学生先独立完成，再在小组里交流（教师出示小组交流注意点，如图1所示）.

生1：我举的例子是5×9=9×5，我发现它们的结果是相等的，所以乘法有交换律.

生2（补充）：我觉得一个例子的说服力不太够，我还举了10×2=2×10，10000×10000=10000×10000……我通过计算发现，两个数相乘，交换乘数的位置后结果仍相等，所以我觉得乘法也有交换律.

（学生献上掌声，教师相继板书：算结果）

生3：我举的例子是2×3=3×2，我画图证明，（边指图边解释）我画的左边是2个圆圈一组，有3组，一共有6个圆圈，右边是3个圆圈一组，有2組，一共有6个圆圈，6个圆圈等于6个圆圈，所以乘法有交换律，如图2所示.

生4（补充）：我举的例子是3×8=8×3，我也画图证明，（边指图边解释）我想到了计算长方形的面积，3×8表示长是8、宽是3的长方形面积，8×3表示长是8、宽是3的长方形面积，结果都是24，所以我也认为乘法有交换律，如图3所示.

（学生献上掌声，教师相继板书：画图示）

生4（再补充）：另外，我还认为3×8表示3个8相加，8×3表示8个3相加，这是从乘法的意义方面想的，结果都是相同的，所以乘法是有交换律的.

（学生献上掌声，教师相继板书：说意义）

师（总结）：同学们真厉害！想到了三种办法，分别是算结果、画图示和说意义，（出示线段图）其实无论画成什么样的图，都可以用乘法的意义来解释，或许我们还能在接下来的研究中发现其他方法（教师补上省略号）.

师：那么这样的例子还能举得完吗？

生（齐答）：举不完.

师：现在，你们能用数学语言说一说到底什么是乘法交换律吗？

生1：两个数相乘，交换两个乘数的位置，积不变.

生2：a×b=b×a.

（学生回忆在之前学习中见到乘法交换律的环节和练习环节略）

片段2：学思结合 让思辨性思维“摸得着”

教师出示研究二：其他的运算中还有交换律吗？请你们想一想、试一试、说一说.A38C4759-205F-4634-AD7C-11164E5A035B

学生先独立研究，再在小组里交流，最后全班汇报如下.

生1：我举的例子是10-10=0，12÷12=1，减法中交换被减数和减数的位置后差不变，除法中交换被除数和除数的位置后商不变，所以我认为加法、减法、乘法和除法都有交换律，但我们组长说这不对，我想知道为什么.

生2（组长补充）：因为我觉得你那两个例子正好符合交换位置，得数不变，可是我举的例子就不符合，我举的是8-7，它并不等于7-8;200-100也并不等于100-200;12÷3也并不等于3÷12;9÷3也并不等于3÷9.像这样不相等的例子还有很多，所以我觉得减法和除法有时有交换律，有时没有交换律.

生3（补充）：我举出了2-1和1-2，2-1=1，可是1沒办法减2，所以我感觉这是无法判断的.

生4（坚定地表明）：我觉得加法和乘法是有交换律的，但是减法和除法没有交换律，如果减法和除法有交换律，它们就应该像加法和乘法那样有举不完的例子，可是这里很明显没有这种举不完的例子.

（学生献上掌声，大家听起来觉得有道理）

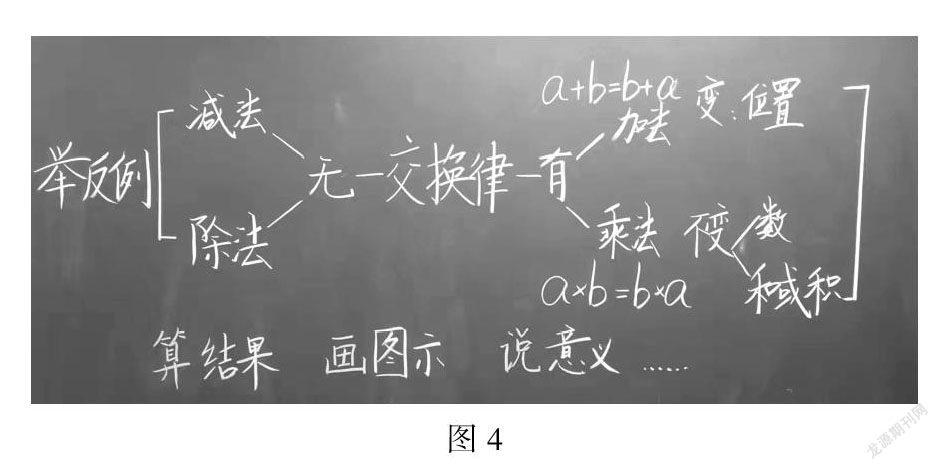
师（评价）：多么会举一反三、思考的孩子们！（点拨总结）刚才第一名发言的学生说到了一组减法算式和一组除法算式恰好符合交换两个数后结果不变的情况，他选择了两个数相同的特殊情况，我们将这样的例子称为“特例”，而我们在研究交换律时一般是两个不同的数.后来，对于组长补充的不满足交换律规律的几个例子，我们称之为“反例”，即只要能举出一个反例就可以说明减法和除法是不满足交换位置后得数不变的情况，因此，我们说减法和除法是没有交换律的.

（教师相继完成结构化板书，如图4所示）

四、提炼认识

本节课研究的是“交换律”，是建立在学生已经经历“观察—猜想—验证—归纳”的探究过程上，大胆鼓励学生在课堂上继续理性地探新奇、辨真伪、明所以然，自然推导至其他运算中交换律的问题.

基于以上的认识，通过本节课，笔者让学生体会到简单的数学知识并不简单，主要围绕以下两点为课堂主线展开教学，并对教学片段进行提炼，现分述如下.

（一）不简单——素养为本：“理解”比“知道”更深刻

现代教学理论表明，数学知识可以分为表层意义和深层意义两个方面.表层意义是指表面的理解，即一些用文字和符号就可以直接表述出来的知识和内容;深层意义是指蕴含在数学知识和内容中或隐藏于知识意义背后的方法、价值、文化意义等.表层意义是逻辑的、显性的和主线的，而深层意义以渗透的、隐性的、暗线的方式存在，是学生核心素养形成和发展的根本.具有生命力的数学课堂需要以发展素养为本，理解学生，理解数学，理解教学.

1.理解学生，符合儿童生长的节律

好奇心是学习的原动力和创新起源，小学生天生好奇，对周围事物会表现出积极的求知欲望，喜欢刨根问底.在“交换律”的教学中，苏教版数学教材中并没有编写减法和除法没有交换律，但是学生在学习加法交换律之后不免产生其他运算是否存在交换律的疑问.这时，通过教师创设的具有适度挑战的情境，学生能在举例证明的研究中不断感受到数学的丰富与简约、神奇与美妙，从而获得思维的进阶体验，形成对数学知识的敏感、好奇和追根究底的学习精神.

2.理解数学，挖掘数学内容的本质

数学史表明，数学是一种形式化的表现方式，它是通过直觉、猜测、反驳、再猜测、再反驳的多次重复过程，最终发现并获得可靠的知识的形式.

在“交换律”的课堂上，学生经历了观察猜想—举例验证—得出结论—再观察猜想—再举例验证—再得出结论……一直循环研究的过程，不仅猜测乘法有交换律，而且使用算结果、画图示和说意义等方法来验证自己的猜测是正确的，在学习环节中收获研究经验，再猜想减法和除法有没有交换律，通过举反例来反驳和验证，最终挖掘出数学知识的本质内涵，如图5所示.

3.理解教学，发现教学内在的规律

教学不等同于讲授知识，但教学一定是以知识为载体，围绕知识的主线展开的.作为单个知识点可能是独立地存在于每一册、每个单元、每个学时中.然而，教师应该对知识的前后联系有着清晰的了解，并且能够在教学中利用结构化的梳理或板书帮助学生建构知识体系.本节课中的板书也是“不简单”的，既有结论性的描述，又有过程性的轨迹表征，既能反映出知识的横向扩展，又能表达出知识的纵向深远.

（二）不简单——思维转向：“会学”比“学会”更重要

在执教本节研究课之前，笔者曾对不同的班级做过前测，第一个问题是“请举例说一说什么是乘法交换律”，结果只有12.5%的学生知道乘法交换律，并能简单地举例说明;第二个问题是“根据加法交换律进行填空：3道类似6×7=（ ）×（ ）的填空题”，结果正确率高达 97.8%.从数据分析中，我们知道学生或许不知道乘法交换律这个名称，却已经感受到乘法交换律的意义且已经会运用，那么在课堂上让学生学会什么、让学生怎样会学的问题势必会困扰着一线教师们.

1.会学，重在积极思考

本节课力求以问促思，用问题促进学生的深度理解，如教师从培养学生的理性思维出发设置了如下两个核心问题：（1）新新在学习的过程中发现3×5=5×3，他认为乘法也有交换律，同学们能试着举出几个这样的例子并选择其中的一个，用画图或自己喜欢的方法解释说明一下吗？（2）其他的运算中还有交换律吗？请同学们想一想、试一试、说一说.第一个核心问题旨在让学生通过多样化的方式表征，深入理解乘法交换律，经历观察猜想、举例验证、得出结论的过程，积累数学活动经验，感悟说理的必要性.第二个核心问题旨在让学生迁移加法和乘法交换律的学习经验，进行其他运算的深度探究，在慎思明辨中发展理性思维.

2.会学，妙在遵循法理

虽然交换律在四年级之前已经用于加法和乘法运算的验算，但一些学生对于交换律的认识和理解仅停留在简单的直觉感知、知识应用和机械的运算技能层面，并没有深入到对交换律的概念内涵、算理的理解层面.本节课在理解加法交换律和结合律之后，并没有单独学习加法交换律，而是将“交换律”的视角打开，向纵向延伸、横向拓展.这一举措反映教师既勇于冲破教材的束缚，敢于整合资源，又有法可循，而学生的知识储备已经能够支撑他们进行科学的探究，加上课堂中简单浅显的学习场景更是让学生产生深度的理解和探究的愿望.

3.会学，贵在交流碰撞

学生小组活动采取先在组内进行交流，再到全班大组里汇报的形式，组内交流时做到“小红笔说到哪儿、指到哪儿、看到哪儿、想到哪儿”，组员每人都要做到“认真听、仔细想，点头鼓掌给个赞，摇头举手做补充”，正是这样平等、开放的学习氛围让学生敢想敢说、敢于质疑、敢于反驳、敢于争论、敢于认错，有理有据地阐述乘法、减法、除法是否也存在交换律的验证过程.学生在交流碰撞中能获得知识上的习得，学会和他人对话，学会和他人合作.

不简单的教学是基于课程标准、高于教材、贴近学生、思维进阶的教学，这样的课堂回归了数学教学的本真，留给了学生心灵激荡的数学思考和永远受用的解决问题的思想方法，体现了教师用智慧让简单的数学知识变得不简单.

【参考文献】

[1]陈淑娟.审问之，慎思之，明辨之：《加法交换律》教学与思考[J].教育视界，2020（17）：46-49.

[2]李洁，李柱俊.浅浅深深：数学教学之道：以“加法交换律和结合津”的教学为例[J].小学教学参考，2020（8）：17-18.A38C4759-205F-4634-AD7C-11164E5A035B