趋势因子与股票横截面收益

潘慧峰 代 盛 袁 军 于京媛

1 引 言

技术分析是金融从业者进行投资的一个重要的分析工具。所谓的技术分析，主要是通过一些图形（比如K线图）或一些技术指标（比如MA、MACD、RSI等），再根据一些交易规则来预测股价未来趋势的方法。业界普遍认为技术分析是有效的，其理论基础是认为历史会重演，一些特定的价格图表能够折射出投资者对市场的看法，当这种图形再次出现时，股票价格走势也会和以前类似。相关调查发现，很多投资者都在大量的使用技术分析来分析股票、期货和外汇市场中资产价格的走势。在进行短线操作时技术分析的实用性甚至超过了基本面分析，给投资者带来了可观的收益。

但技术分析的科学性从一直饱受学术界的质疑，按照有效市场假说的逻辑，所有信息都已经在价格中反映了，任何技术分析都是徒劳的。但技术分析成功实践也促使学术界重新审视经典金融学理论，提出了一系列的理论模型对其进行解释，比如噪音理性预期模型、BSV理论模型、DHS理论模型、羊群模型、混沌模型等，这些理论从侧面证明了技术分析存在合理性。

与技术分析最相关的市场异象为动量异象。从直观上，动量和技术分析均认为市场没有达到弱式有效，个股和指数可能存在趋势。在技术分析领域，Fung和Hsieh（2001）［1］发现移动均线指标能预测股票未来收益，趋势追踪策略是解释对冲基金收益的重要原因。Brock 等(1992)［2］、Neely等(2011)［3］均发现均线指标具有显著预测能力，其预测效果无论从统计上还是经济效益上都强于基本面指标。国内实证研究也支持均线指标具有预测能力（孙碧波 2005［4］；韩豫峰等 2014［5］)。在理论上，Zhu和Zhou(2009)［6］从资产配置的角度证明了移动均线策略是投资者在面临不确定环境下比较好的投资分析工具，Han等（2016）［7］进一步采用均线指标构造了趋势因子（Trend Factor），该因子的构造利用了股价短期、中期和长期信息，结果发现该因子能更好的解释股票横截面收益。

伴随着改革开放的推进，中国资本市场得到了较快发展。截止至2021年底，沪深两市的上市公司超过四千家，我国证券市场已经成为世界第二大证券市场。与发达国家的证券市场相比，中国股市投资者中“散户”较多，专业性不强，投机等非理性行为突出。相比机构投资者，个人投资者在获取公司信息方面比较困难，再加上投机心理，使得交易时更多的依赖技术分析而不是基本面分析，这使得技术分析指标在中国市场具有较强的预测能力。

以上论述表明，在散户投资者为主体的中国股票市场，技术指标是否有助于预测股票收益率？基于技术指标构造的趋势因子是否更适合我国资本市场？本文拟采用A股上市公司的数据检验Han等(2016)的趋势因子是否适用于A股市场，本文丰富了技术分析在新兴市场资产定价的实证证据，同时对证券市场的监管提供借鉴。

2 理论基础

相关金融理论认为：股票价格存在趋势，利用股票交易的技术分析指标能对未来收益进行预测。

从理性角度分析，Grossman和Stiglitz (1976)［8］认为信息的获取需要成本，这些成本信息不会立刻从价格中反映出来，因此市场有效性降低，人们可以通过一些历史信息判断股价未来趋势；Treynor和Ferguson(1985)［9］及Brown和Jennings(1989)［10］构造了两阶段的噪音理性预期模型，该模型指出噪音所带来的不确定性会阻碍当前价格对信息的揭示，价格的历史信息有助于预测未来收益；Soros（2003）［11］认为市场存在正反馈效应，股价上升会改善公司的基本面，好的基本面又会促使股票价格进一步上升，从而产生价格趋势，一些对冲基金经理也会根据此效应构造投资策略。

从投资者行为偏差角度分析，投资者并非完全理性，他们对自己私有信息的过度自信以及自我归因偏差，或者对新出现的信息的反应过度和反应不足，导致股票价格形成趋势。一些理论模型也被提出来解释这种趋势，Barberis等(1998)［12］提出的BSV模型认为投资者的保守主义(conservation)和代表性偏差(representive)，导致对信息存在反应不足和反应过度，从而形成价格趋势；Daniel等(1998)［13］建立的DHS模型则认为投资者对自己私有信息的过度自信和自我归因偏差导致股价的偏离与反转；Hong和Stein(1999)［14］提出的HS模型则认为动量交易者的动量交易行为容易使股价产生趋势。由于股票市场存在趋势，根据技术分析预测股价走势就存在可能。

但上述研究只是从市场非有效的角度对技术分析有效性进行逻辑演绎分析，并没有对均线指标这一技术指标有效性进行实证分析，更没有给出趋势因子具有预测能力的理论依据。Zhu和Zhou(2009)基于资产配置视角，从理论上证明了在不确定情况下，均线策略能为投资者创造更多额外收益。随后，Han等（2016）在理论上引入了均线策略交易者，证明了在静态理性均衡状态下，资产价格的均衡价格的表达式为：

其中p0，p1，p2，p3和p4为常数，Dt为股利流(Dividend flow)，πt为股利流均值（mean level of dividend flow），θt为资产的供给，他们分别满足如下随机过程

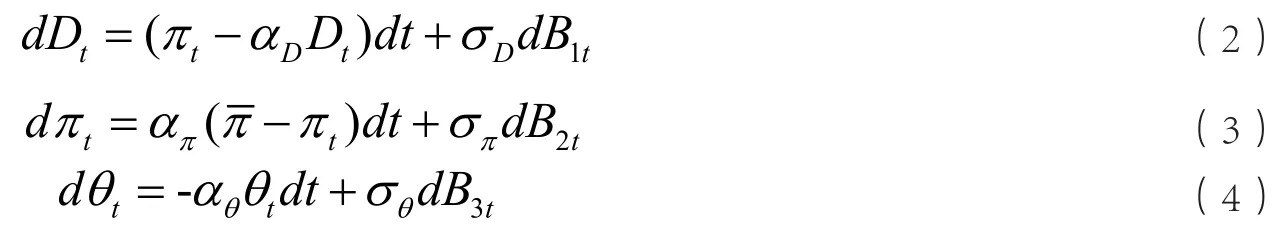
由均衡模型可知，资产价格是均线指标At的线性函数，p4可正可负，大小取决于市场中均线策略交易者的比例。将式（1）做一阶差分得：

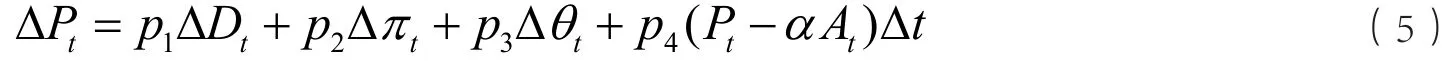
然后等式两边除以资产价格得到：

从式（6）可以看出，当市场中存在均线策略交易者的情况下，资产收益率是资产归一化均线指标的函数。因此，归一化的均线指标对股票未来的收益率具有预测能力具有坚实理论基础。

3 趋势因子构建

3.1 数据来源

本文以2003年1月至2016年12月A股上市公司为研究样本，个股的收盘价、换手率、市值、账面市值比数据来自Wind数据库，无风险利率和Fama-French三因子数据来自CSMAR数据库。本文采用周数据进行分析，周收盘价为该周最后一个交易日的收盘价计算。由于趋势因子的计算（具体计算过程见下文）需要用到235日均线指标以及52周回归系数的均值，最初两年得不出预期收益，因此实际有效样本区间为2005年至2016年，共606周的数据。

3.2 趋势因子计算

基于技术指标构造趋势因子的步骤如下：

步骤一：计算归一化均线指标

每周最后一个交易日归一化的均线指标计算如式（7）所示：

MA(Pj,t,Li)为t周最后一个交易日的日均线指标，指标参数为Li，本文选取6个参数，分别为3日，5日，10日，7日，20日，60日，120，和235日。这些参数计算的指标包含了短期，中期和长期的均线指标，反映了股价短期、中期和长期信息，Pj,t为股票j在t周最后一个交易日天的收盘价（后复权处理）。之所以要归一化处理，主要有以下三点原因：第一，从理论上讲，归一化的均线指标对股价收益的预测性更好；第二，从统计学的角度，归一化的均线指标更具有稳定性；第三，归一化均线指标可以消除股价异质性的影响，比如茅台股价达到上千，而中国银行股价只有几块钱，股价相差太多对方程回归系数影响很大。

步骤二：估计回归系数。在t周，以t-1周归一化均线指标为解释变量，t周的收益率作为被解释变量，建立线性回归方程，采用最小二乘法进行横截面回归，得到t期的回归系数βi,t，回归方程如式（8）所示：

步骤三：计算个股预期收益。根据t周归一化的均线指标和过去N周（包含本周）回归系数的均值，计算该股票在t+1期预期收益。预期收益方程如式（9）所示：

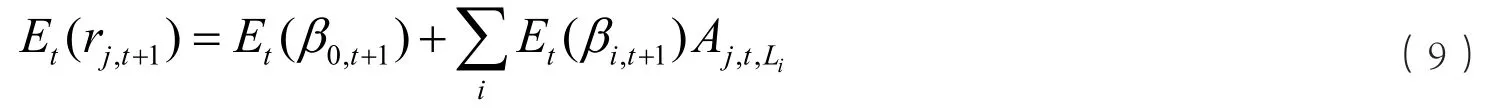
其中Et(βi,t+1)为过去N期回归系数的均值，计算表达式如下：

由于Et(rj,t+1)是根据趋势技术指标计算得出，因此本章将Et(rj,t+1)定义为股价的趋势因子。按照研究市场异象的标准做法（Jegadeesh和Titman，1993［15］），根据每只股票趋势因子的大小对市场中的股票排序，以10分位数为节点，将市场中的股票分成10组，按照等权重组合的方式构造10个投资组合，做多趋势因子最高组，做空趋势因子最低组，该多空组合收益为趋势因子收益，持有一周后进行再平衡，以此向前滚动，得到趋势因子收益时间序列，检验该收益的显著性。

4 单变量排序

4.1 描述性统计

图1给出了不同参数的均线指标的回归系数在过去52周的移动平均值随时间的变化关系，从图中可以发现回归系数的移动平均值相对较稳定。回归系数有正有负，说明市场存在不同程度的动量效应和反转效应。

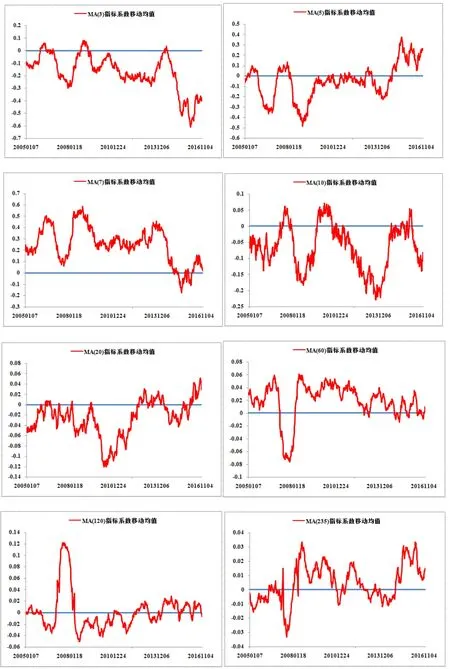
图1 归一化均线指标回归系数52周均值

为了突出该因子的优点，本文还将该因子的收益和其他常见因子的收益进行比较，具体包括Carhart四因子模型中四个风险因子收益，即市场收益（Market），市值因子收益（SMB），价值因子收益（HML），和动量因子收益（MOM）。一些学者研究发现，中国股票市场存在短期反转效应，潘莉和徐建国（2011）［16］利用2002年至2008年的数据，发现中国市场普遍存在一周反转现象，对上一周股票收益排序，构造多空组合并持有一周，平均能获得28.72%的年化收益，齐玉录和王志强（2015）［17］将数据扩展到了2014年，得到了相同的结论。因此本文还计算了样本区间内一周反转效应的收益，具体做法为：对市场股票上周收益排序，分成10组，每组等权重组合，构造10个投资组合，做空收益最高组，做空收益最低组，持有一周后再平衡，多空组合的收益为反转因子收益（Reversal）。

表1报告了各个因子收益之间的Pearson相关系数和Sperman相关系数，左下角为Pearson相关系数，右上角为Sperman相关系数。从表中我们发现Trend因子收益与其他因子收益相关系数都不高，说明趋势因子收益与其他因子收益相关性不大。与Reversal因子收益的相关系数最高，Pearson相关系数为0.23，Sperman相关系数为0.37，其次是与MOM 因子收益的相关系数，Pearson相关系数为-0.24，Sperman相关系数为-0.18，与其他因子收益的相关系数都没有超过0.1，可能的原因在于趋势因子、MOM因子、Reversal因子都是量价数据计算而得，他们之间的相关性要高些。

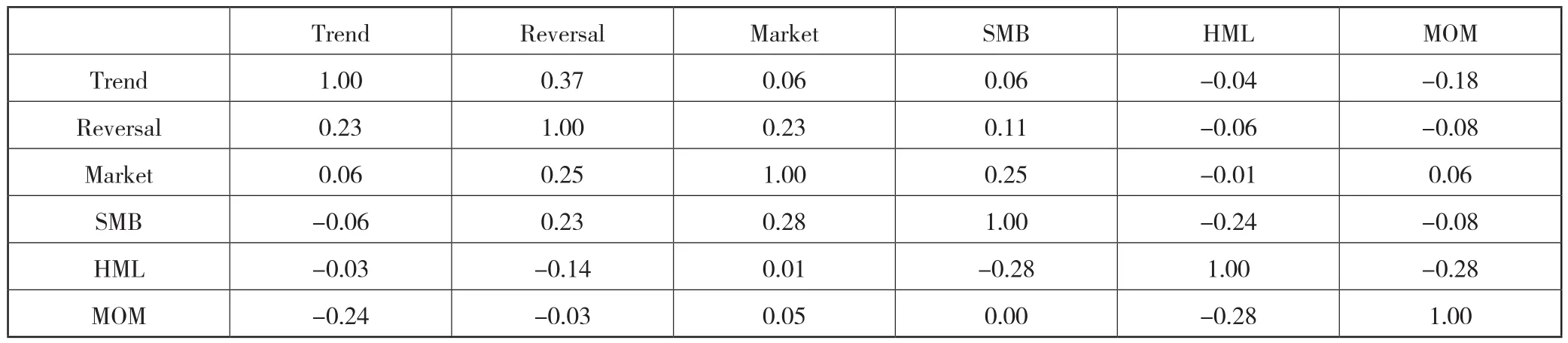
表1 各个因子收益的相关系数

表2 给出了各个因子收益的描述性统计，从表中可以看到Trend因子收益最高，每周平均收益为1.21%，对应t统计量为8.40，在1%置信水平下显著，初步说明该因子对股票截面收益具有预测能力；其次是Reversal因子收益，每周平均收益为0.8%，对应的t统计量为7.07，在1%置信水平下显著，说明中国股票市场存在反转效应； Market因子和SMB因子的平均收益分别为0.34%和0.38%，说明市场存在风险溢价和小市值效应，而HML因子和MOM因子收益没有通过显著性检验，说明中国股票市场不存在显著的价值效应和动量效应。从标准差可以看出，各个因子收益标准差区别不大。从偏度来看，Trend因子收益偏度为1.68，在各个因子收益中最大，说明根据该因子获得较大收益的概率更大。

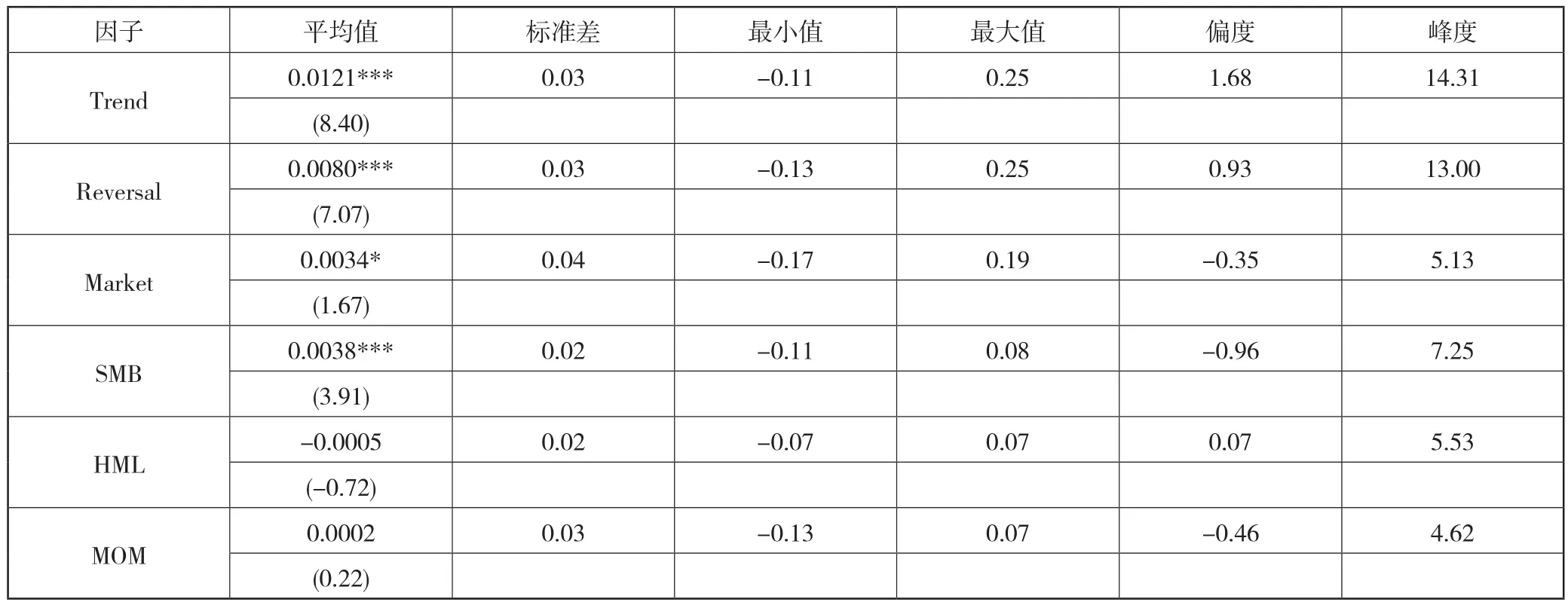
表2 描述性统计

4.2 风险收益分析

前面给出各个因子收益的描述性统计，但没有考虑风险因素。为了进一步考察各个因子风险收益情况，本小节采用因子总收益、最大回撤、年化夏普比率（年化收益和年化风险比）和Calmar比率（年化收益与最大回撤比）来衡量各个因子的绩效。表3报告了相应的实证结果，从表7.4的结果中可以发现，12年的时间里，趋势因子总收益高达11282%，是市场因子收益（343.60%）的数十倍；同时，该因子的最大回撤只有16%，远小于其他因子的最大回撤，由于趋势因子的高收益，低波动和低回撤，使具有较高的夏普比率（2.90）和较大的Calmar比率（3.73），二者都是其他因子的数倍。

表3 各个因子的绩效分析

为了观察各个因子每年的表现，表4给出了各个因子每一年的收益，从表4可知，趋势因子每年的排名表现比较稳定，一直排在前三名以内，而且每年总收益也都为正，表现出了很好的稳定性。其他因子的排名不稳定，收益有正有负。比如反转因子收益，在2009年时表现最好，每周平均收益为1.32%，排名第一，但在2014年，每周平均收益为-0.05%，排名最后。

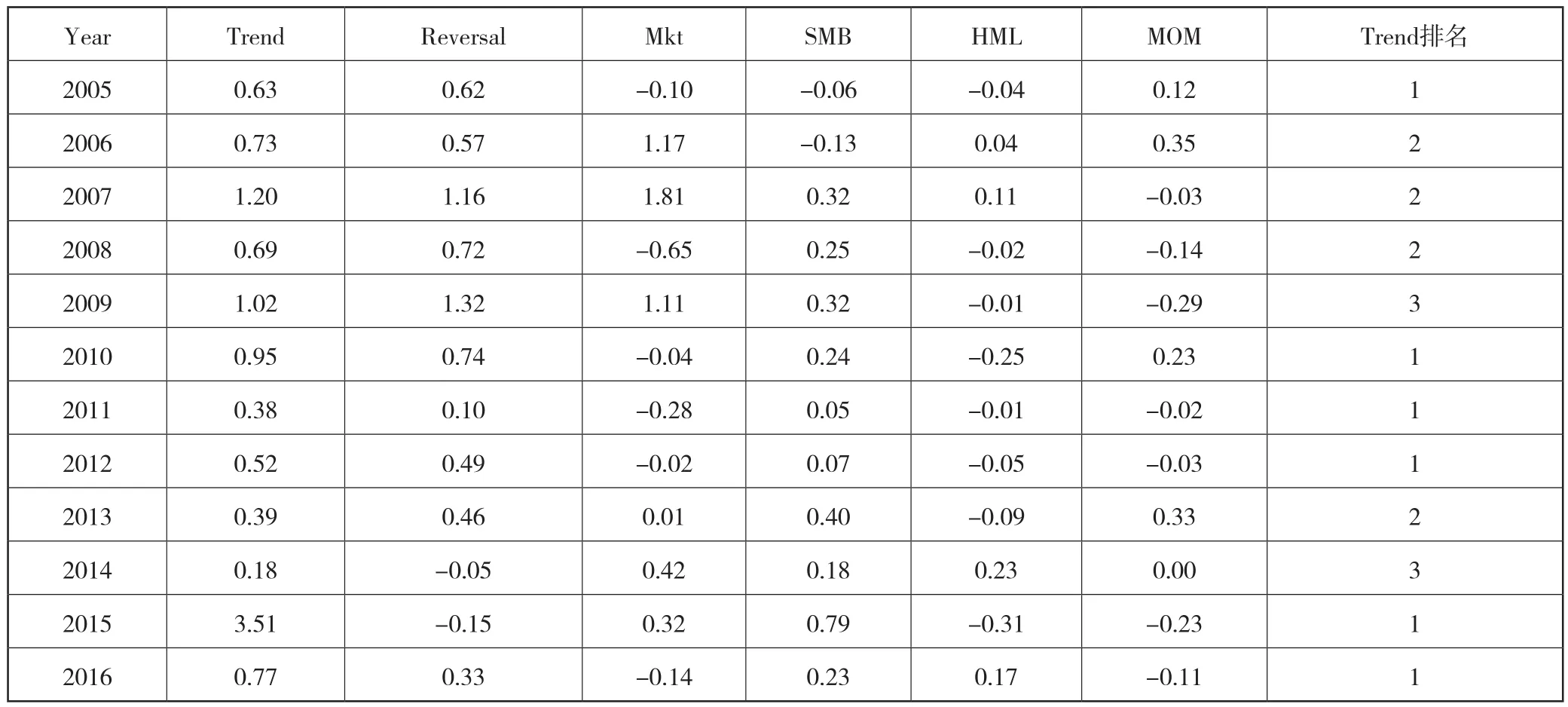
表4 各个因子每年的收益表

4.3 α收益

根据趋势因子构造的投资组合的收益可能来源于一些风险，因此需要对投资组合的收益进行风险调整，常用的风险调整的方法为进行CAPM和Fama-French三因子调整。表5给出了各个投资组合经过CAPM模型和Fama-French三因子模型调整后的α收益实证结果。从表5可以看出，10个投资组合的α收益从趋势因子最低组到最高组依次递增，CAPM模型调整后的每周α收益从最低组的-0.5%逐渐递增至0.69%，高低组合的α收益差为1.19%，对应的NW-t统计量为7.70，在1%置信水平下显著。Fama-French三因子模型调整后的每周α收益从最低组的-0.67%逐渐递增至0.57%，高低组合的α收益差为1.23%，对应的NW-t统计量为6.58，同样在1%置信水平下显著。多空组合收益经过CAPM模型和Fama-French三因子模型风险调整后依然存在显著的α收益，这说明，传统的资产定价模型不能解释该因子的收益。

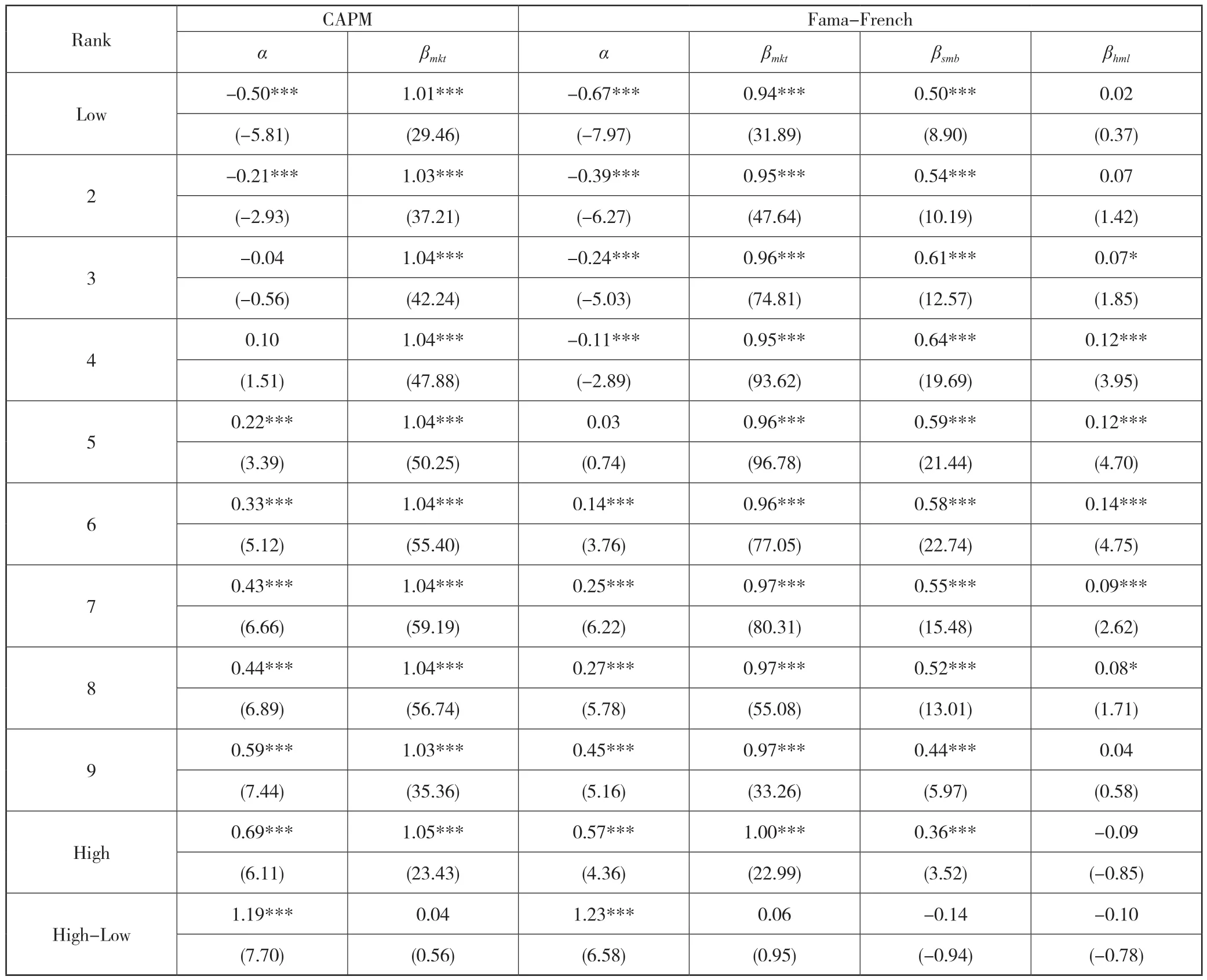
表5 经过CAPM模型和Fama-French三因子模型调整后的收益

5 稳健性检验

为了检验趋势因子对股票截面收益的预测性，本小节将做以下稳健性检验：（1）改变参数，检验结果对参数的敏感性；（2）分样本区间（2005年-2010年、2011年-2016年）（3）进行双变量排序，检验在控制其他预测变量情况下，趋势因子的预测性是否还存在（4）进行Fama-MacBeth回归，检验在控制其他一系列变量后，趋势因子的预测性是否还存在。

5.1 改变参数

1.改变N

上节以过去52周回归系数均值作为预测下周收益的预测系数，接下来考察结果对参数N的敏感性。表6给出不同参数N下，相应投资组合每周的平均收益和风险调整后的α收益。从结果中可知，趋势因子依然对股票的横截面收益具有预测能力，高低组的收益差依然非常显著。以N为26周为例，高低组间的收益差，CAPM调整后的α收益和Fama-French三因子模型调整后的α收益分别为0.99%，1.00%和1.02%，对于的NW-t统计量分别为7.20，6.91和6.22，在1%置信水平下显著。从表6中我们还可以发现，N越大，多空组合的收益越稳定，说明多期回归系数的均值能更准确的预测。

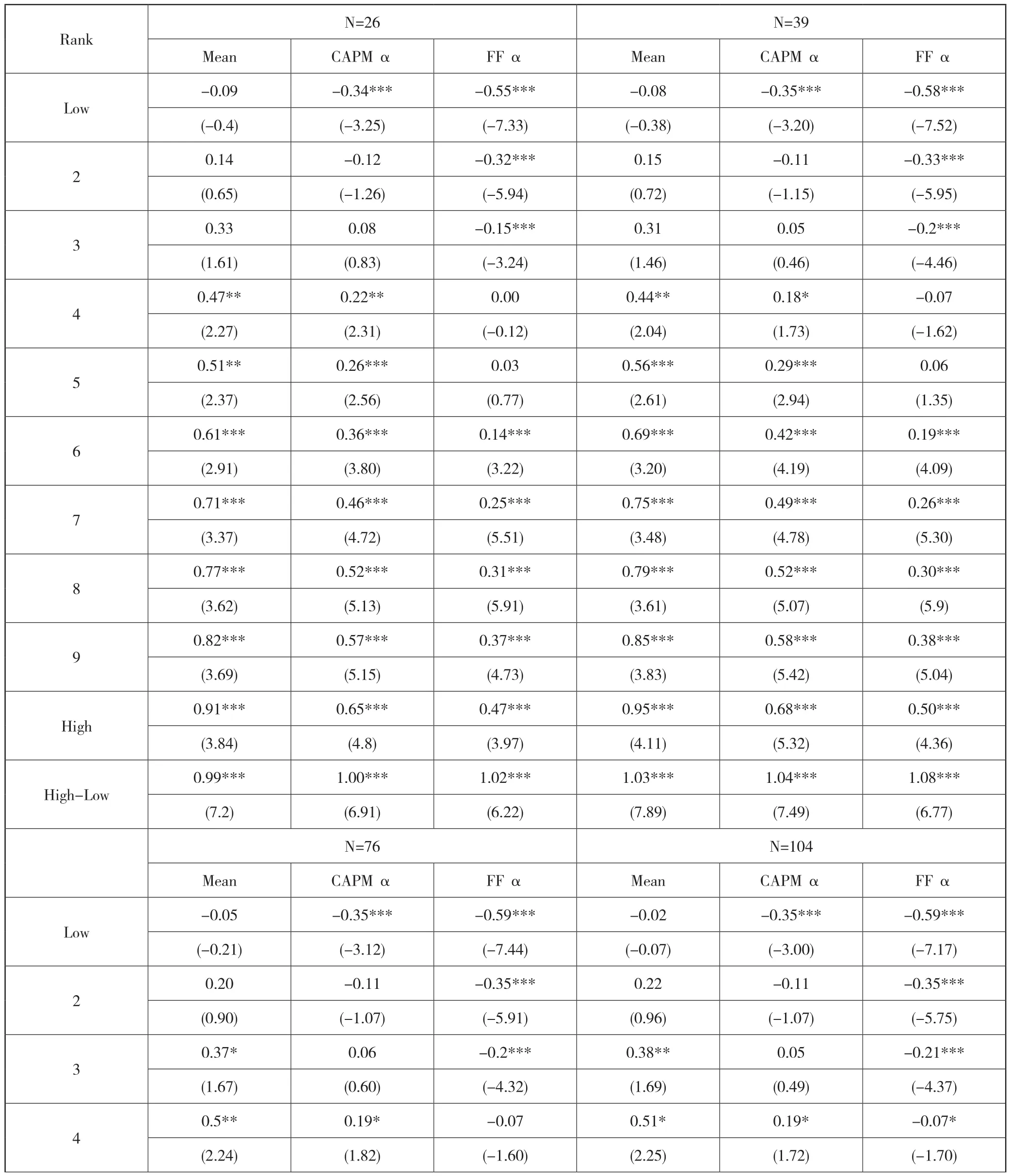
表6 改变参数N时的实证结果

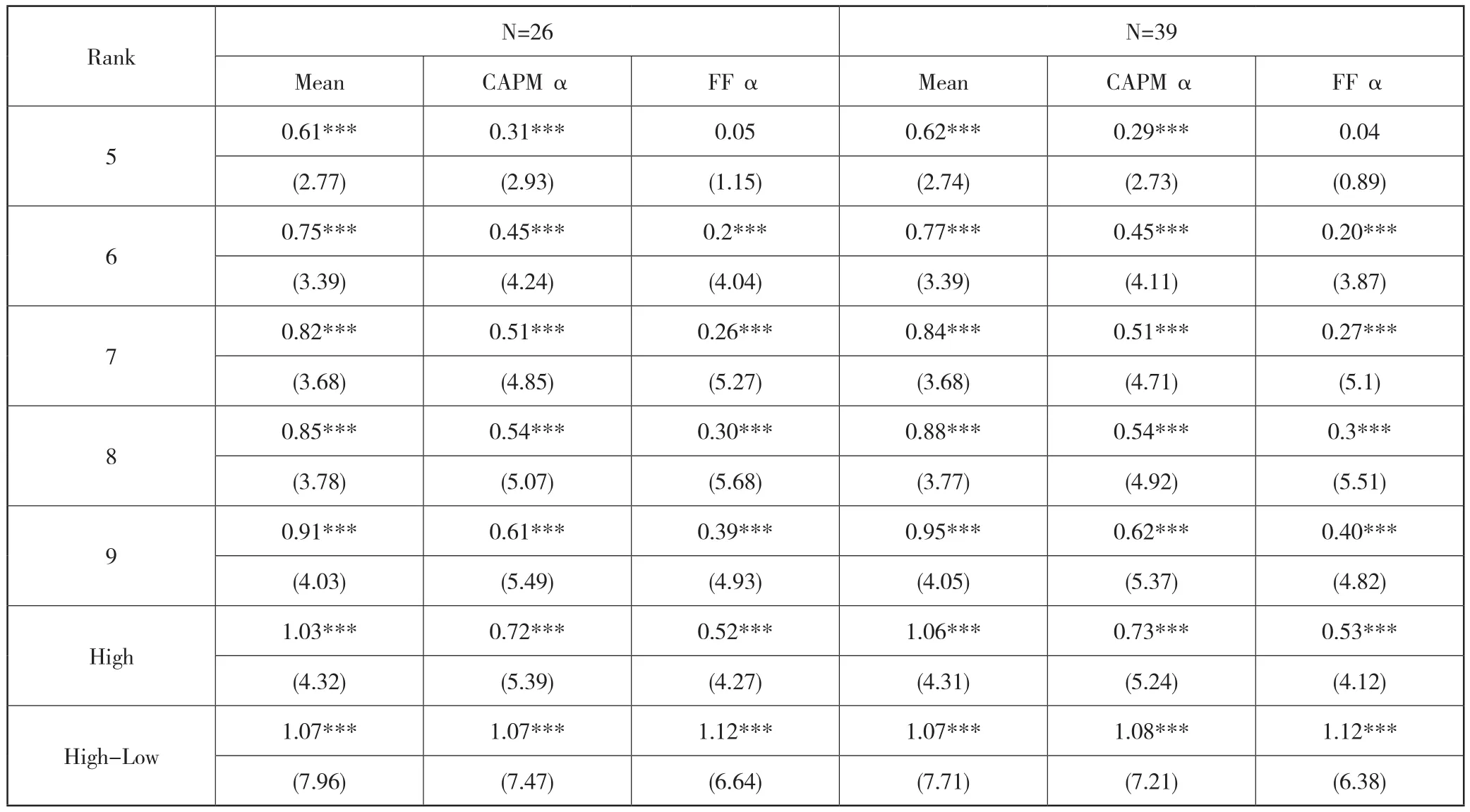
续表

2.改变均线指标参数

上文的技术指标分别为3日、5日、7日、10日、20日、60日、120日和235日八个均线指标，为了检验技术指标参数的敏感性，本文通过改变（Lag = ［ 3 5 7 10 20 50 100 235］，Lag = ［ 3 5 7 10 20 60 120 200］）、减少（Lag = ［ 3 7 10 20 60 120 235］）和增加（Lag = ［3 5 7 10 20 90 60 120 235］）技术指标参数的方法对其进行检验。由表7可知，趋势因子依然对股票的横截面收益具有预测能力，高低组的收益差依然非常显著，以技术指标参数Lag = ［ 3 5 7 10 20 50 100 235］为例，高低组间的收益差，CAPM调整后的α收益和Fama-French三因子模型调整后的α收益分别为1.22%，1.21%和1.22%，对于的NW-t统计量分别为8.43,7.98和7.30，在1%置信水平下显著。说明该因子对技术指标参数并不敏感。

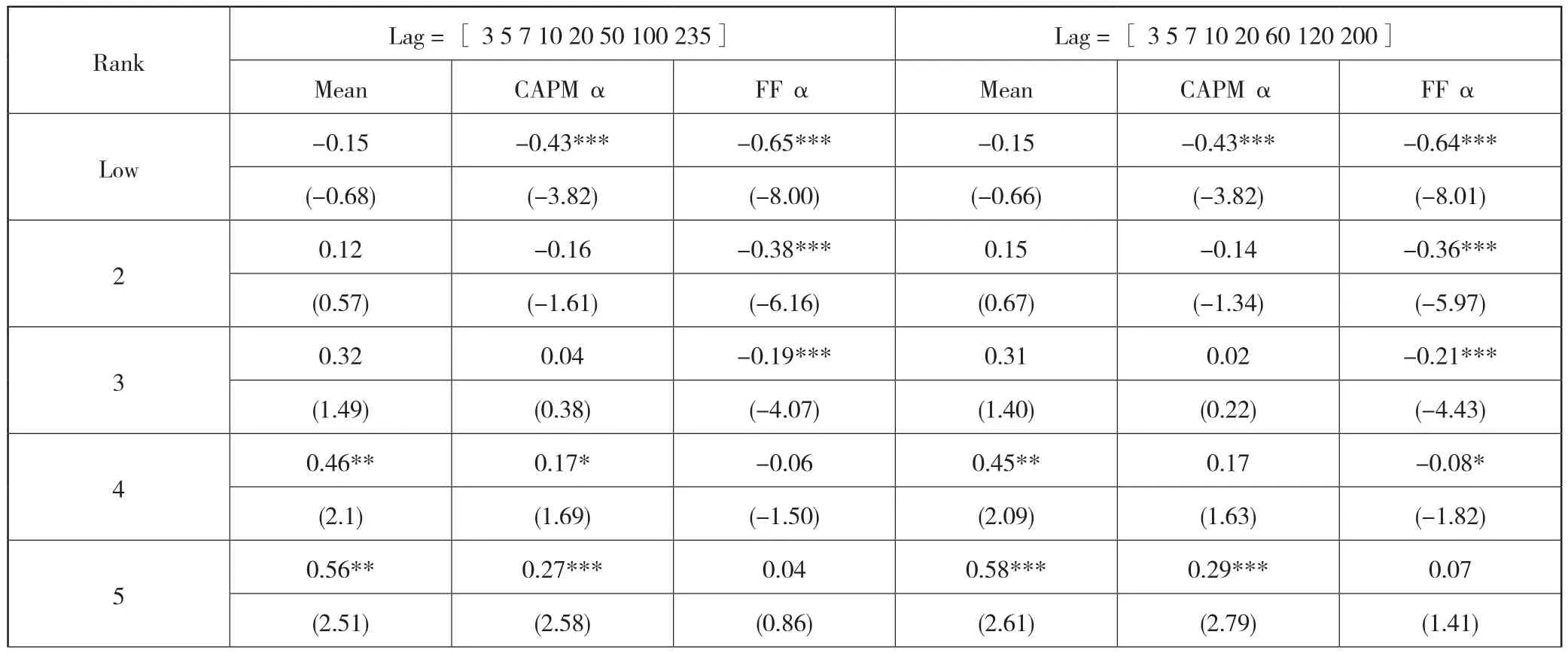
表7 改变技术指标参数Lag的实证结果

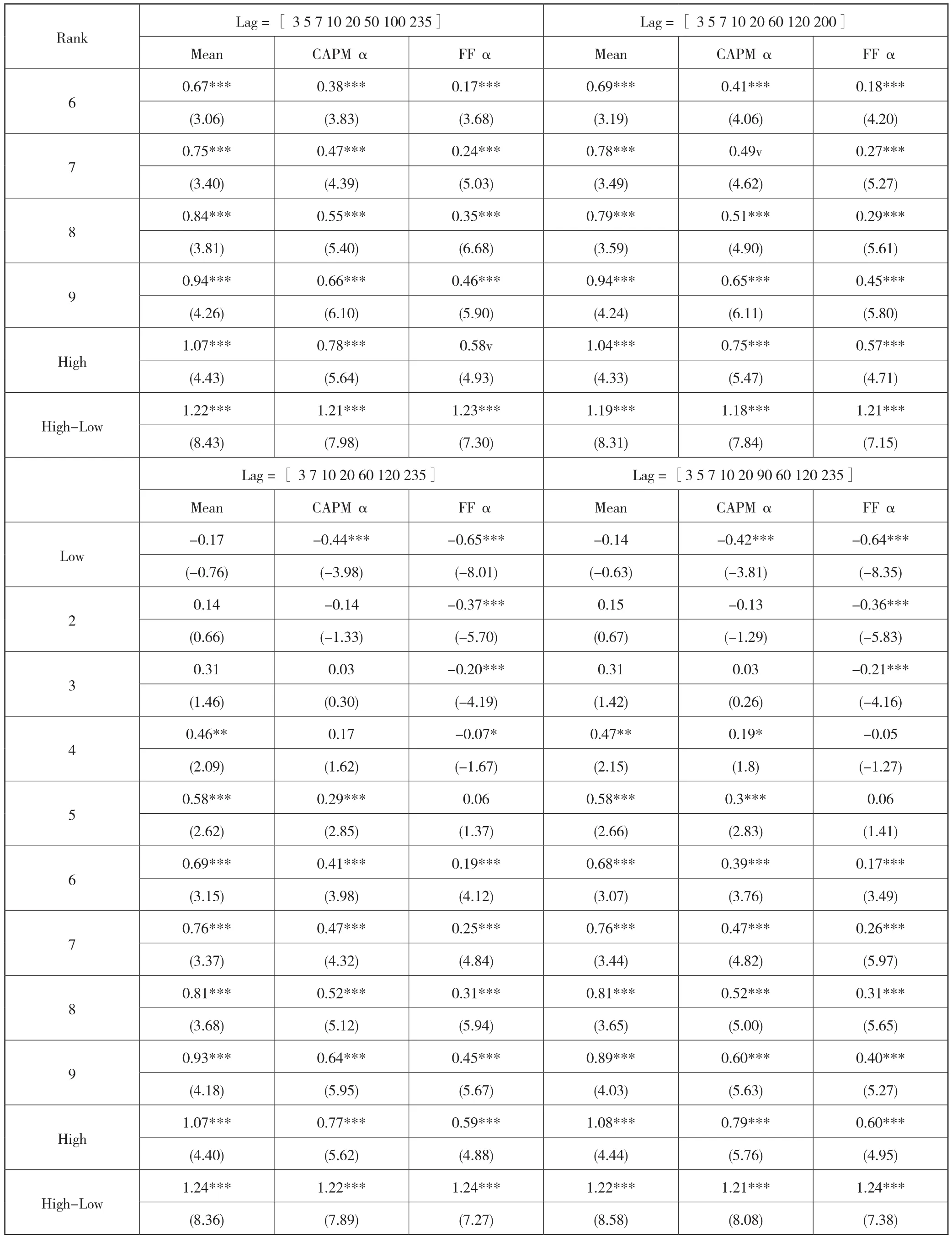
续表

5.2 分样本区间

表8汇报了2005年-2010年和2010年-2016年趋势因子的预测能力，实证结果表明，趋势因子在两个时间段依然具有显著的预测能力，高低组之间的收益差依然很显著。在2005年-2010年区间内，高低组间的收益差，CAPM调整后的α收益和Fama-French三因子模型调整后的α收益分别为1.29%，1.25%和1.25%，对于的NW-t统计量分别为8.50，8.24和7.84；在2011年-2016年区间内高低组间的收益差，CAPM调整后的α收益和Fama-French三因子模型调整后的α收益分别为1.12%，1.13%和1.20%，对于的NW-t统计量分别为4.60,4.47和4.00，都在1%置信水平下显著。

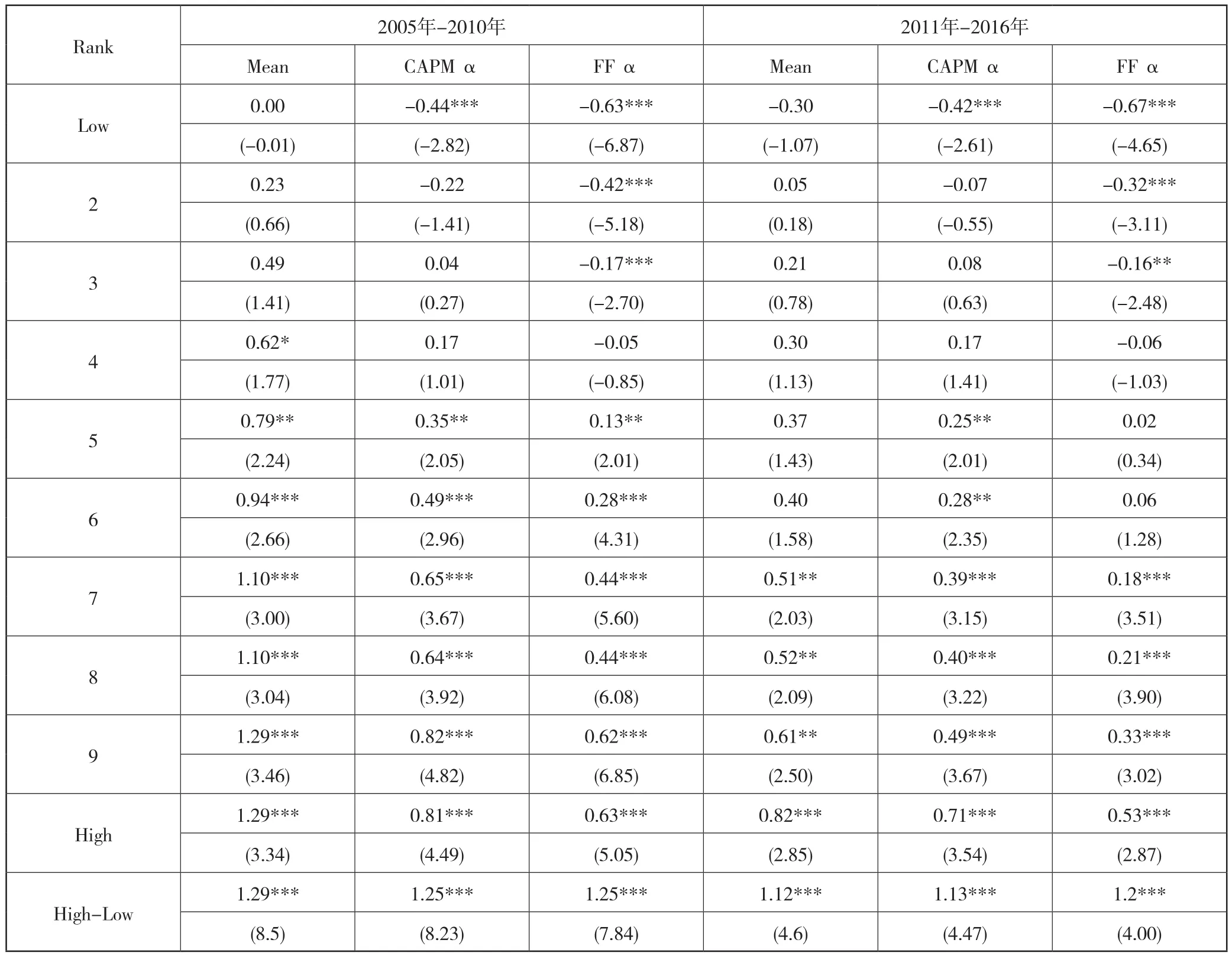
表8 不同样本区间的实证结果

5.3 双变量排序

为了进一步说明趋势因子对股票横截面收益具有预测能力，通常需要应用双变量排序法检验在控制一些其他的预测因子下，比如公司的市值，账面市值比等，趋势因子是否还具有预测能力。

在控制公司市值情况下，检验趋势因子是否还具有预测能力为例。首先根据公司的市值，将市场中的公司分成5组；然后在每组中再根据趋势因子，又分成5组，得到5*5组投资组合，将每组中的股票等权重组合，得到5*5个投资组合的收益。

表9为控制公司市值Size（以上周最后一个交易日的市值计算）后趋势因子对股票横截面收益的预测性，从表10中可以看出，趋势因子在小市值组的表现最好，高低组每周收益差为1.18%，对于的NW-t统计量为8.40，随着市值的增加，趋势因子的表现逐渐减弱。在市值最大组，高低组每周的收益差为0.71%，但差异依然非常显著，NW-t统计量为5.50，通过求平均值，控制市值影响后，趋势因子高低组之间的收益差为0.98%，NW-t统计量为9.39，在1%置信水平下显著。说明在控制公司市值后，趋势因子依然对股票横截面收益具有预测性。

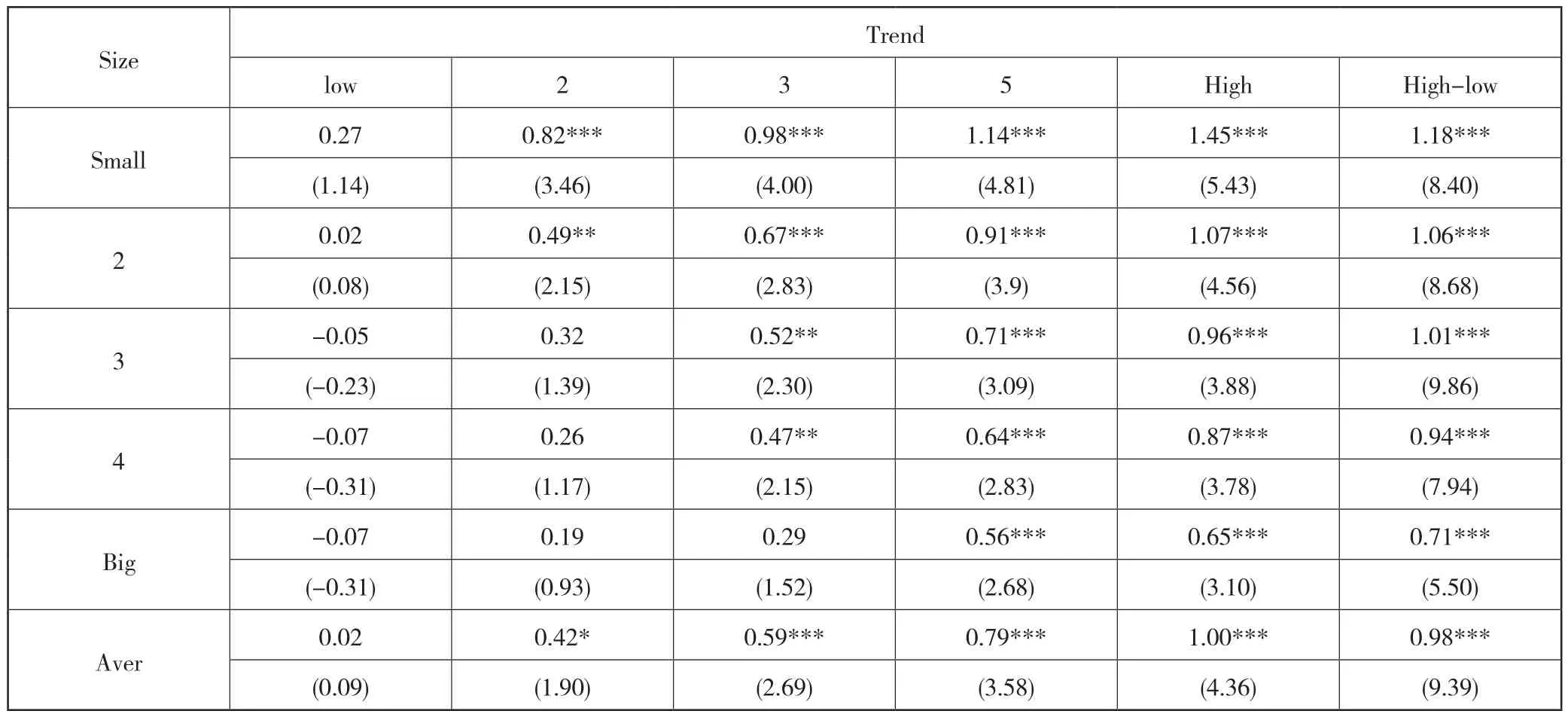
表9 Size和Trend进行双变量排序

此外，本文还控制了其他变量进行了检验，控制的变量包括公司股票的Beta值（以过去三年公司周数据计算得出），公司股票上周收益（R_1），公司上周末最后一个交易日账面市值比对数（BM=1/PB），公司上周股票换手率（Turnover）。实证结果表明，趋势因子对股票横截面收益的预测性仍然存在。限于篇幅，实证结果不在正文报告。

此外，表10和表11还给出了在控制其他变量的情况下，各个投资组合经CAPM模型和Fama-French三因子模型风险调整后的α收益。实证结果表明，趋势因子对股票横截面收益的预测性依然没有发生改变。比如在控制公司市值的情况下，高低投资组合CAPM模型风险调整后的α收益为0.97，NW-t统计量为9.75；Fama-French模型风险调整后的α收益为0.99，NW-t统计量为7.81，都通过显著性检验。

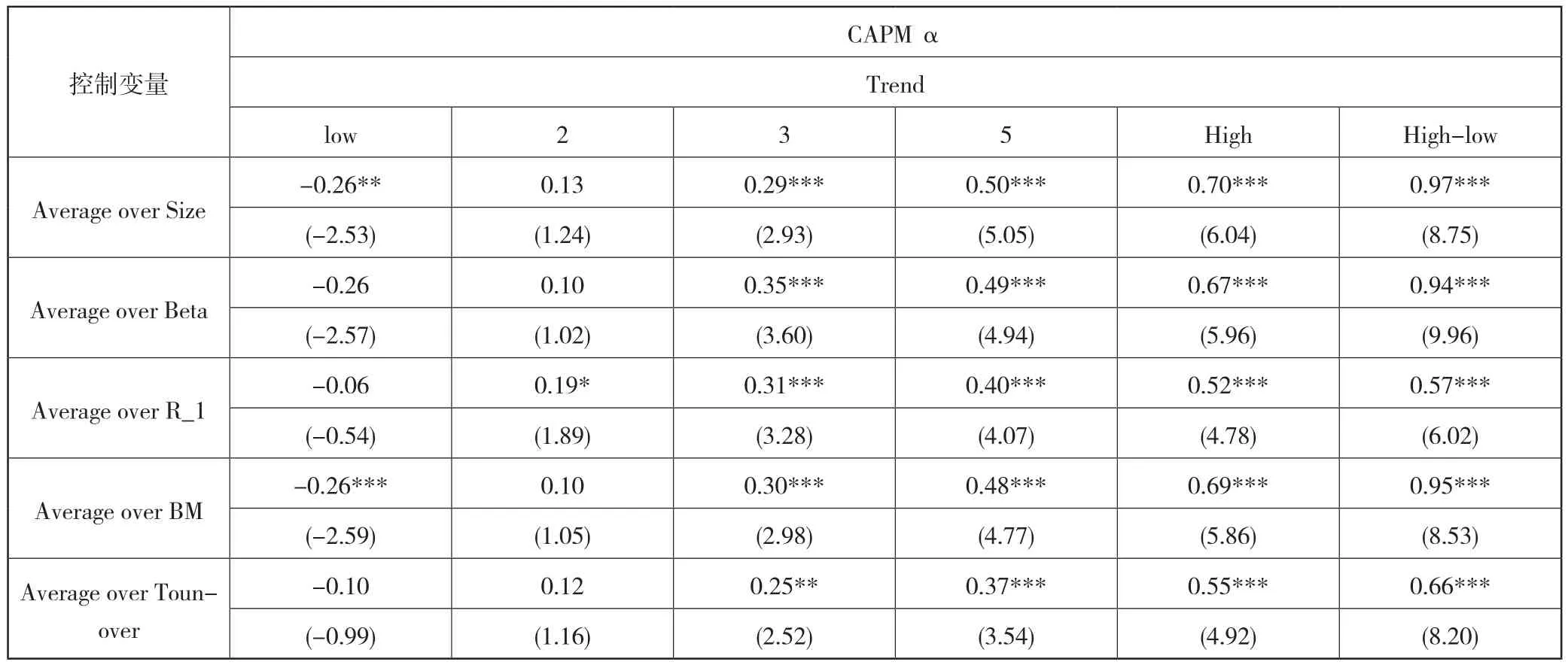
表10 CAPM模型风险调整后的α收益

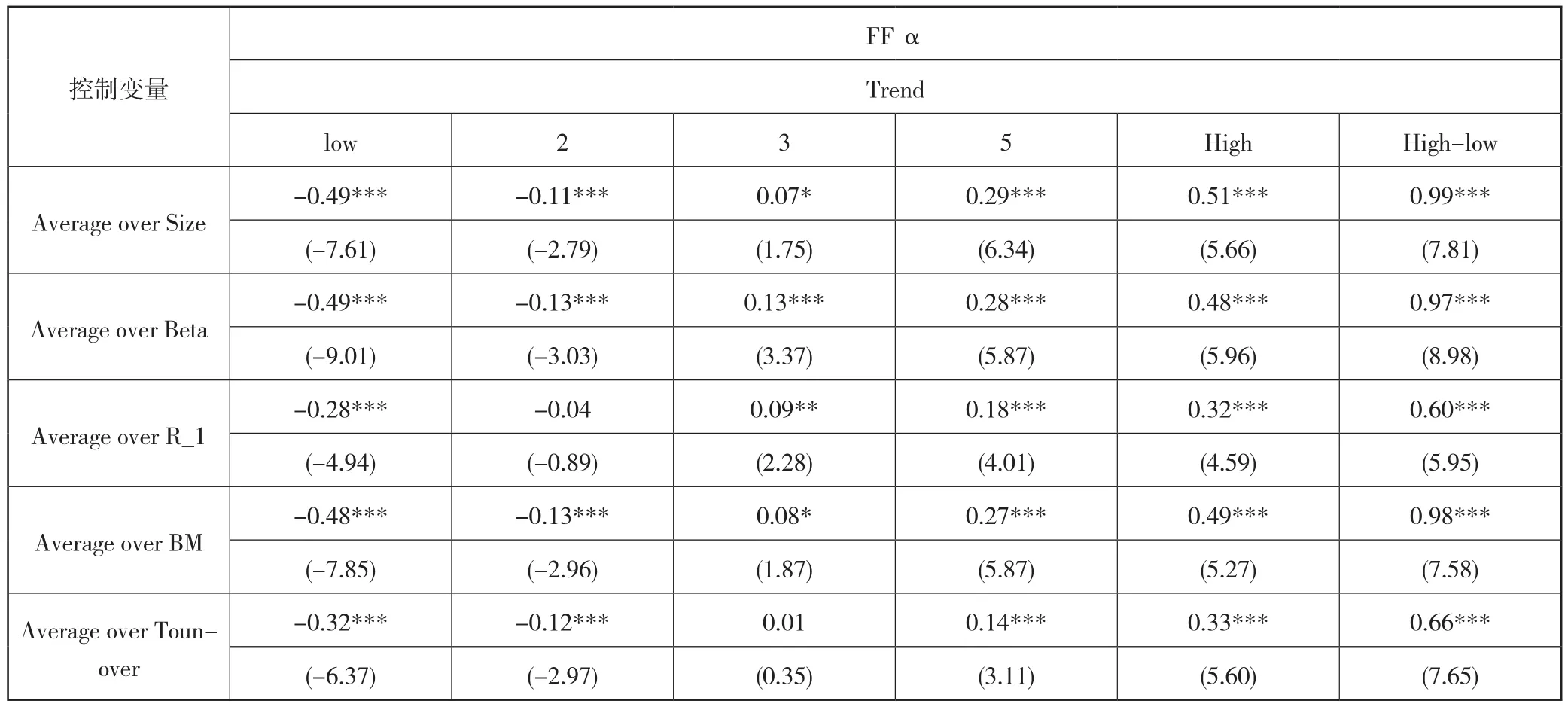
表11 Fama-French三因子模型风险调整后的α收益

5.4 Fama-MacBeth回归

双变量排序法能检验控制其他变量后，趋势因子是否还具有预测能力，但该方法只能控制一个变量，如果想进一步控制多个变量，需要采用Fama-MacBeth回归法分析。

表12汇报了股票的周收益率对趋势因子和其他控制变量的横截面回归结果，回归方程（1）检验了单个趋势因子的预测能力，回归系数为0.86，t统计量为12.21，1%置信水平下显著。回归方程（2）至回归方程（6）检验在增加一个控制变量的情况下趋势因子的预测性，结果发现趋势因子的回归系数均显著为正；方程（7）和（8）在控制其他所有变量后的情况下，结果都发现趋势因子的回归系数均显著为正。

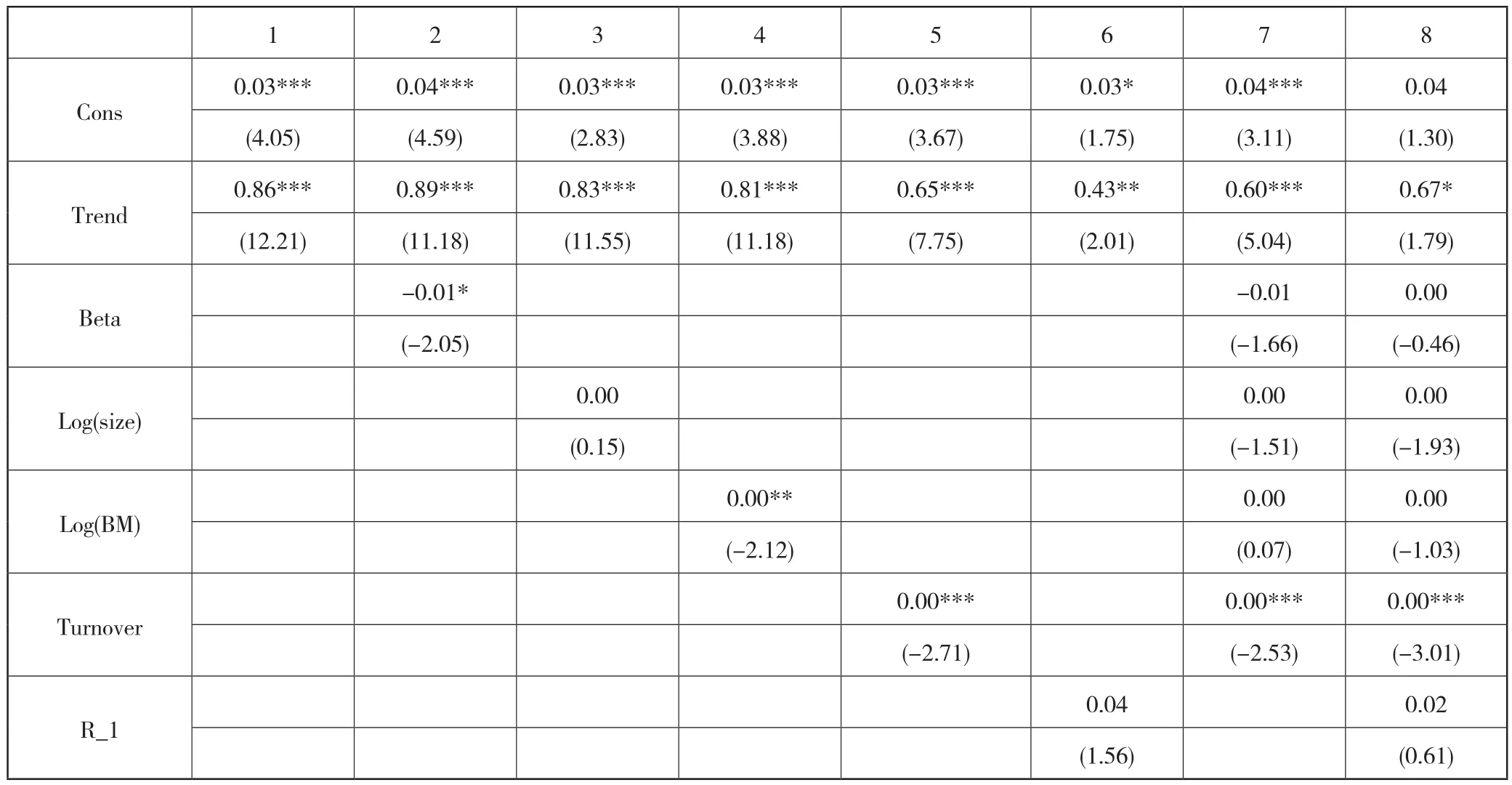
表12 Fama-MacBeth回归结果

6 结 论

本章采用归一化的均线技术指标，构造每只股票趋势因子，根据该因子对市场的股票排序分组，构造多空组合，实证发现：（1）趋势因子对股票横截面具有较高的解释力，趋势因子可以获得显著的超额收益；（2）与常见的反转因子、市值因子、动量因子、价值因子、市场因子相比，趋势因子的收益最高；（3）控制其他横截面变量情况下，趋势因子的预测能力依然存在；（4）经过CAPM模型和Fama-French三因子模型风险调整后，依然存在α收益。