基于GPS/BDS/GLONASS/Galileo 的区域CORS 稳定性分析

陈国恒，涂纯二*，刘远海，陈梅森

（1. 广东省国土资源测绘院，广东 广州 510500）

利用全球导航定位系统（GNSS）基准站网或CORS 站来建立与维持高精度全球或区域地心动态坐标框架是最普遍的方法[1]。截至目前，全国已有不少省市和地区[2-14]利用美国的GPS观测数据进行CORS站网的稳定性分析，验证了GPS 能实现坐标框架的建立、维护、稳定性监测以及地壳运动的运动趋势分析，是最可靠的GNSS 观测数据来源。随着中国BDS的全球组网，以及俄罗斯GLONASS 和欧盟Galileo 的逐步发展，利用GPS、BDS、GLONASS、Galileo 等多源卫星系统观测数据进行CORS 站网坐标框架的维持是未来的发展趋势。鉴于现有文献较少利用多源卫星系统进行区域框架维持研究，本文以2018—2019年的HKCORS 观测数据为例，分别求取BDS、GLONASS、Galileo的坐标时间序列，并以GPS数据处理结果为参照，验证比较了利用BDS、GLONASS、Galileo进行坐标框架稳定性分析的可行性和可靠性。

1 数据处理方案

1.1 数据来源

本文选取香港卫星定位参考站网（SatRef）系统的8 个CORS 站，分别设立在山顶和楼房天台位置，其中山顶站点设有5 m 高的支柱和安全围栏，避免受到人为干扰，站点间距离约为10~15 km，时间跨度为2018—2019年，该段时间测站设备状态稳定。需要说明的是，在该时间跨度测站设备暂不能接收BDS-3信号，因此本文数据均采用BDS-2观测数据。站点分布如图1所示。

图1 CORS站点分布图

1.2 解算策略

本文采用GAMIT 和GLOBK10.71 进行基线解算和平差计算，为保证客观评价不同卫星系统下数据处理情况，基线解算时在sittbl表设置以HKKT站为先验坐标约束，其他解算策略与过程采用默认模式执行[15]。广播星历均采用多模GNSS实验跟踪网（MGEX）提供的混合星历产品，GPS、GLONASS 采用IGS 精密星历，BDS、Galileo 采用武汉大学IGS 数据中心的多星混合精密星历。平差计算则选择相对稳定的山顶站HKKT站、HKLT站、HKNP站作为起算基准，获得其余站点每日的坐标值，生成坐标时间序列，再通过函数模型进行线性拟合，最后生成区域CORS 的水平和垂直速度场。关键解算参数控制与文件表如表1所示。

表1 关键解算参数控制与文件表

2 稳定性分析

2.1 基线解算

本文通过数据计算获得了2018—2019 年GPS、BDS、GLONASS、Galileo 的基线解算结果。结果表明，个别单天解由于星历文件和测站观测数据的缺失可能存在未探测的周跳修复和模型错误，均作剔除处理。本文利用GAMIT 解算的标准化均方根误差（NRMS）检核判定各卫星系统下的数据解算质量。NRMS统计结果如图2所示，整体来看，GPS解算结果最稳定，解算质量最好；BDS次之，平均解算质量优于GLONASS、Galileo，但个别单天解的NRMS 值较离散，可能是受精密轨道和钟差文件精度不稳定的影响。

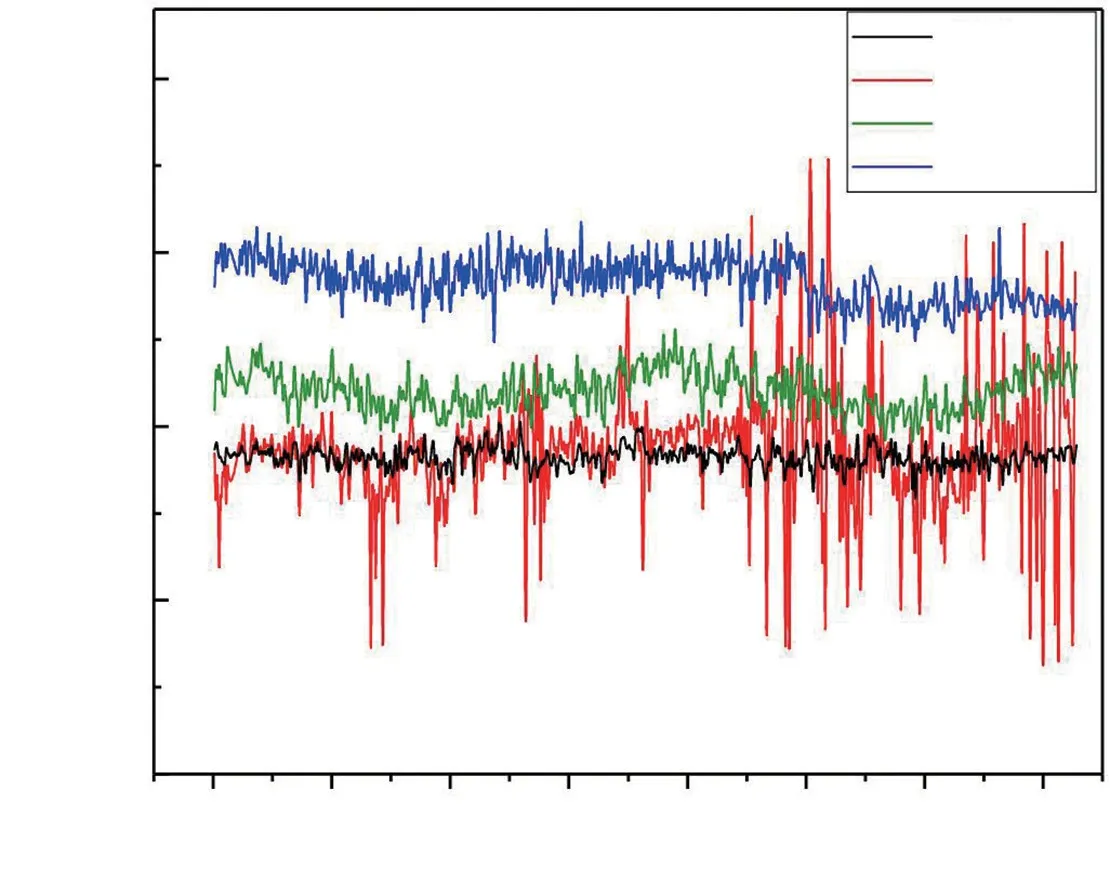
图2 各系统的NRMS值

本文从基线向量重复性方面进一步分析解算的质量，结果如表2 所示，a、b 分别为基线重复性的固定误差和比例误差，可以看出，GPS在各方向上的固定误差和比例误差均优于BDS、GLONASS 和Galileo；其他3 个系统在N 方向、E 方向和基线长度上较接近；而BDS 在U 方向上的基线重复性略低于其他系统。

表2 基线向量重复性统计/mm

2.2 坐标时间序列

本文首先分别将各系统所有获得的正常基线解成果文件h-file合并，并运行GLRED模块获得测站点的坐标时间序列；再通过分析具有坐标异常值的测站或天数删除坐标异常的h-file；然后再次运行GLRED 模块获得各测站合格的GPS、BDS、GLONASS、Galileo坐标时间序列。限于篇幅，本文仅列出HKKS 站的坐标时间序列图（图3）。

由图3可知，各系统在坐标时间序列E、N方向上的波动范围均小于U方向，说明水平方向的坐标平差精度优于高程方向，其中GPS 的坐标平差精度更高，因此GPS 在各方向上的波动范围整体小于BDS、GLONASS和Galileo。

图3 GPS、BDS、GLONASS、Galileo的坐标时间序列

采用GLRED模块获得的时间序列包括加权均方根误差（WRMS）和NRMS两项精度评定指标，WRMS的单位为mm，NRMS 为无量纲。HKKS 站GPS、BDS、GLONASS、Galileo 的 WRMS 和 NRMS 值统计结果如图4所示，可以看出，GPS在各方向上的WRMS值均优于其他系统，而NRMS值的差异并不明显。

图4 坐标时间序列精度统计

为了拟合滤波后获得的坐标时间序列，本文对各站坐标分量的单日解序列建立以下函数模型[9]：

式中，ti为以年为单位的时间；a 为序列线性项的截距；b 为线性速率；c、d 和e、 f 分别为年周期和半年周期项的运动振幅；gj为同震跳动等引起的阶跃式坐标突变；hj为震后运动速度的改变量；kj描述震后变形呈指数衰减的现象； H( t )为阶跃函数；τj为指数震后松弛时间常数；vi为残差，假定vi与时间无关（高斯白噪声）。

由于本区域测站不存在阶跃项和震后项的影响，即测站时间序列只有速度项和周期项，由此获得拟合后的GPS、BDS、GLONASS、Galileo 坐标时间序列。限于篇幅，本文以HKKS 站为例进行对比分析，结果如图5 所示，可以看出，拟合后的GPS、BDS、GLONASS、Galileo坐标时间序列的线性变化和周期变化更直观，均呈现一定的季节性变化；在E 方向，GPS 的标准方差为2.36 mm，最大、最小值极差为7.56 mm，BDS 的标准方差为2.86 mm，最大、最小值极差为8.49 mm，GLONASS 的标准方差为2.34 mm，最大、最小值极差为7.66 mm，Galileo 的标准方差为2.34 mm，最大、最小值极差为7.78 mm，在该方向具有较一致的区域相似性；在N 方向，GPS 的标准方差为1.05 mm，最大、最小值极差为3.31 mm，BDS的标准方差为2.02 mm，最大、最小值极差为6.80 mm，GLONASS 的标准方差为1.39 mm，最大、最小值极差为4.68 mm，Galileo的标准方差为1.17 mm，最大、最小值极差为3.72 mm，在该方向GPS、GLONASS、Gali⁃leo的一致性较好，BDS稍逊于其余3个系统；在U方向，GPS的标准方差为1.01 mm，最大、最小值极差为3.56 mm，BDS 的标准方差为3.28 mm，最大、最小值极差为11.62 mm，GLONASS 的标准方差为1.27 mm，最大、最小值极差为4.46 mm，Galileo 的标准方差为1.02 mm，最大、最小值极差为3.68 mm，在该方向GPS、GLONASS、Galileo 的一致性较好，BDS 明显逊于其余3个系统。

图5 GPS、BDS、GLONASS、Galileo拟合后的坐标时间序列

本文通过运行GLOBK 模块获得GPS、BDS、GLONASS、Galileo的速度值和精度统计，结果如表3、4所示，可以看出，与GPS相比，BDS、GLONASS、Gali⁃leo 的速度值精度差异不大，且精度较高；再画出GPS、BDS、GLONASS、Galileo 相对于约束基准站的水平方向和垂直方向速度场，如图6、7所示。

表3 GPS、BDS速度场值与精度统计/（mm/a）

由图6、7可更直观地反映各系统的速度场大小和方向，可以看出，GPS、BDS、GLONASS、Galileo 各测站的相对水平运动总体均向海域方向移动，若以GPS 为参照对比，HKKS 站和HKTK 站一致性相对较好，均向东南方向移动，HKSC站、HKLM站和HKCL站各系统的水平速度场变化存在一定差异；HKKS 站一致性相对较好，均为向下沉降，其他站点的GPS、BDS、GLONASS、Galileo 在垂直方向均存在上升或沉降。总体来看，各系统运动变化结果均符合CHT 2011-2012《全球导航卫星系统连续运行基准站网运行维护技术规范》中基准站的平面位置变化不超过2 cm或高程变化不超过3 cm的规定，说明本文解算的5个HKCORS站的稳定性良好。

图6 测站水平方向速度场

表4 GLONASS、Galileo速度场值与精度统计/（mm/a）

图7 测站垂直方向速度场

3 结 语

本文利用2018—2019 年的区域CORS 观测数据，对GPS、BDS、GLONASS、Galileo 进行数据处理，获得了各系统的坐标时间序列。经对比分析发现，GPS的基线解算质量和时间序列处理精度均优于其余3 个系统。利用GLONASS、Galileo观测数据获取的坐标时间序列基本与GPS保持了区域一致性，BDS稍逊于其余3 个系统。从区域CORS 的稳定性监测来考虑，基准站的位置变化均在规范范围内，因此利用BDS、GLONASS、Galileo进行坐标框架稳定性分析是可行和可靠的。当然，本文还存在一定的局限性：①本文旨在从区域CORS 稳定性方面进行监测分析，忽略了有色噪声的影响，速度值可能有所偏差；②BDS已全面组网，然而由于基准站卫星接收设备有待更新等原因，无法获得BDS-3观测数据，导致本次数据处理的BDS整体精度低于GPS。