基于IEMD和GA-WNN的断路器分合闸线圈故障诊断方法
2022-06-06李天辉庞先海范辉甄利顾朝敏董驰
李天辉,庞先海,范辉,甄利,顾朝敏,董驰
(1. 国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2. 国网河北省电力有限公司,河北 石家庄 050021)
0 引 言
在系统故障或者非故障情况下,断路器应能关合、开断、承载运行回路运行电流[1-5]。因此,当断路器出现故障时,不仅会对其所保护和控制的下级电网造成严重损坏,而且会引起上级电网的扰动,造成电网不稳定,严重时甚至可能引起大面积停电事故,对社会各行业造成巨大的损失[6]。然而,断路器大部分工作在室外,受工作环境影响,慢慢老化而逐渐影响其可靠性[7-8]。因此,提高断路器故障诊断能力具有实际工程价值。
目前,常见故障诊断技术主要分为两大类:一类是数学诊断方法,如概率统计分析法[9]、小波分析法[10]、灰色系统诊断法[11]等;另一类为智能诊断法,主要是基于智能算法的单一诊断方法,如小波神经网络 (wavelet neural network, WNN)[12]、支持向量机[13]、极限学习机[14]、D-S证据理论[15]等,或由多个智能算法组合的混合算法[14,16]。
在文献[16]中,首先构建了分合闸线圈电流特征样本库,再利用粒子群算法进行故障诊断,其不同的断路器故障识别率高达100%。文献[17]通过对不同故障下的分合闸线圈电流波形进行分析,以及故障模拟,进而提取出不同断路器个体之间的电流特征。文献[6]根据断路器分合闸线圈电流信号特征建立诊断识别模型,并利用卷积小波神经网络算法进行故障诊断,其故障识别率高达93.68%。
由上述文献研究不难发现,在智能算法辅助下,现有诊断技术取得长足发展,识别率不断提高。但现有故障识别技术的准确率主要基于改进智能算法的性能和特征值提取的准确率。基于此,本文主要从断路器典型故障电流曲线库、特征值提取和智能诊断方法等方面进行研究,与现有研究相比,主要贡献有:(1)对断路器典型故障进行实验室模拟,得到典型故障的分合闸线圈电流曲线,为后续构建故障特征曲线样本库提供了基础。(2)根据电流信号经过经验模态分解 (empirical mode decomposition,EMD)后的IMF能量密度乘对应平均周期为恒定常数的性质,提出一种改进经验模态分解(improved empirical mode decomposition,IEMD)方法来提取分合闸线圈电流特征值,该方法能有效剔除原始信号中的噪声干扰和IMF伪分量,进而提高特征值提取准确率,为后续故障诊断提供有效的输入样本集。(3)利用改进遗传算法(genetic algorithm ,GA)对WNN初始权值等敏感参数进行寻优,可解决WNN算法参数敏感问题,有效提高收敛速度和寻优能力。
1 真空断路器分合闸线圈工作过程
弹簧操动机构真空断路器的分闸操作、合闸操作过程如图1所示,是一个动态过程,当分合闸线圈接收到通电信号,将带动分闸/合闸触发器顺时/逆时针旋转并释放主拐臂上的轴销A或棘轮上的轴销B,完成分合闸动作[18]。从图1中不难发现,每次断路器动作时,都伴随着规律性的分合闸电流产生,分、合闸线圈电流波形分别如图 2 a)和图 2 b)所示。
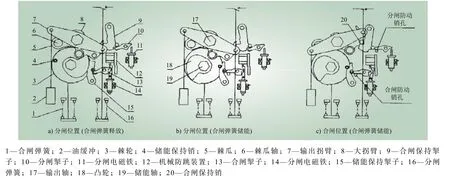
图1 真空断路器分合闸操作机构示意Fig. 1 Schematic diagram of vacuum circuit breaker opening and closing operation mechanism
根据图2,分合闸线圈电流具有明显参数特征,且电流趋势大致相同,分成多个阶段。如在分闸线圈电流中:在t0~t1阶段,线圈得电,二次回路导通,电流迅速上升,铁芯开始运行;在t1~t2阶段,由于需要克服铁芯运动时的阻力,电流降低,当到达t2时刻后,铁芯脱扣,停止运动;进入t2~t3阶段后,由于铁芯静止,电流回升增大;在t3~t4阶段,t3时刻,断路器动触头分离,线圈失电,电流瞬间下降至零[16]。而合闸过程,由于速度比分闸慢,可能存在t3~t4一个稳定阶段,其余部分类似。
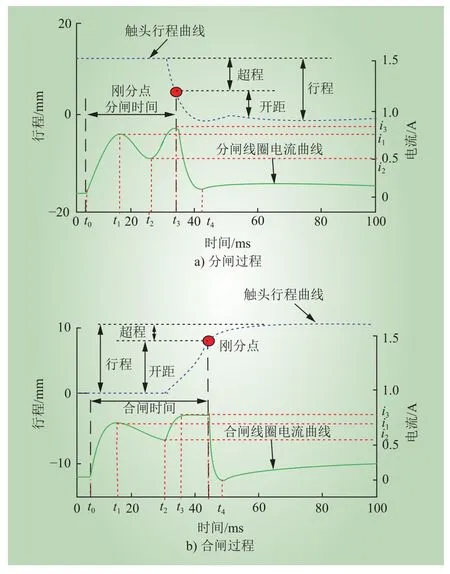
图2 触头行程曲线与分合闸线圈电流曲线Fig. 2 Contact travel curve and opening and closing coil current curve
2 基于IEMD故障特征参数提取模型
2.1 分合闸线圈故障电流特征模拟
大量实验和工程数据表明,常见的分合闸线圈故障主要有分合闸线圈铁心卡涩、电压异常(过高或过低)和击穿3种[18],因此,本文主要对该3种故障状态进行实验分析。具体实验设计步骤如下。
(1)线圈铁心卡涩实验设计流程。由于部分真空断路器安装在裸露的环境中,受空气湿度、潮热等环境因素影响,线圈、电磁铁等零部件会发生锈蚀、老化等恶化现象,进而增大铁芯运动的阻力,出现卡涩故障。在实验中,为定量提取分合闸线圈在不同卡涩程度下的分闸线圈电流特征曲线,将断路器分闸线圈垂直安装,当铁芯向上运动时,通过在分闸线圈铁芯下施加重物的方式,来模拟铁芯运动时受到不同的阻力情况,如图 3 所示。分别施加了 80 g、160 g、240 g、320 g等不同重物进行模拟实验。

图3 不同卡涩程度模拟实验示意Fig. 3 Schematic diagram of core blockage experiment
(2)线圈电压异常(过高或过低)实验设计流程。真空断路器分合闸线圈额定电压为DC220 V,但由于工作环境不同,标准规定分合闸线圈在电压幅值为143~253 V内安全可靠工作即可。但是电压异常(过高或过低)对断路器使用带来不同程度影响,为此,为定量提取线圈电压异常(过高或过低)下分合闸线圈电流特征曲线。在实验室中,通过电压调节器改变分合闸线圈接入电流来模型电压异常实验,如图4所示。

图4 线圈电压异常(过高或过低)实验示意Fig. 4 Schematic diagram of abnormal coil voltage (too high or too low) experiment
(3)线圈击穿实验设计流程。真空断路器中分合闸线圈每次动作时,都会产生热量,不仅加速线圈老化速度,同时也增大了线圈电阻和热量,严重时发生击穿故障,甚至烧毁。为提取击穿状态下分闸线圈电流特征曲线,在实验室中,让分闸线圈长时间通电,直至表面焦黄,发出烧焦异味,但未完全烧毁来模拟分闸线圈击穿故障,如图5所示。

图5 线圈击穿实验示意Fig. 5 Schematic diagram of coil breakdown experiment
2.2 IEMD特征参数提取模型
2.2.1 EMD 信号分解模型
经验模态分解(EMD)过程相当于一种“筛分”操作,将一个信号最终分解为满足以下2个条件的若干个经验模态分量(IMF)[19]。
(1)数据序列中,极值点数量必须等于过零点的数量或相差不超过一个。
(2)任一时间点上,局部放电极值包络线平均值等于零。
EMD 具体分解的过程如下。
(1)求解原信号x(t)的极值点,并利用3次样条插值方法,来拟合x(t)的上包络线u(t)和下包络线v(t)。
(2)从x(t)中减去u(t)和v(t)的平均值,进而得到新的特征信号。
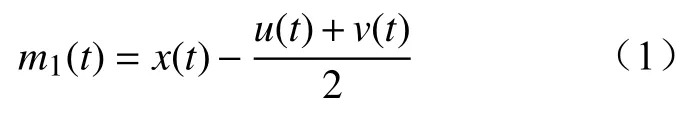
(3)判断m1(t)是否满足IMF分量条件,若不满足条件,则当作输入信号返回步骤(1),继续执行,得到信号m2(t),再次判断m2(t)是否满足条件,不满足则重复执行上述步骤,直到mk(t)满足IMF特征条件。并将其记为C1(t),作为原始信号的第一阶IMF分量。
(4)将C1(t)从原始信号中剔除,得到余量信号,记为r1(t)。
(5)将r1(t)作为步骤(1)的输入信号,重复执行,直到rn(t)函数单调,分解结束。则原始信号用分解信号可表示为

2.2.2 IE MD 信号分解模型
由于EMD电流信号降噪分解过程中,主要依据经验去除第1个IMF分量和第2个IMF分量重构的电流信号,具有较强主观性。因此,本文基于分解后的IMF分量能量密度与其对应的平均周期的乘积是一个常数的性质,提出一种自适应选择IMF分量的重构算法。其具体步骤如下。
(1)在原始信号x(t)中分别添加均值为零的白噪声qi(t)和-qi(t),得到一组新的原始信号序列,即

式中:ai为白噪声幅值;n为白噪声对数。
(2)利用 EMD 分解x1−i(t)、x2−i(t),获得第一阶 IMF 分量序列C1−i(t)和C2−i(t),计算平均值得
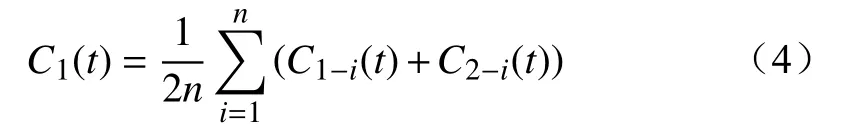
(3)计算通过EMD分解后的若干个IMF分量的能量密度和平均周期之积,即

式中:Ej是第j个IMF分量的能量密度;Tj是第j个IMF分量的平均周期。
(4)计算系数RPj(j> 1)
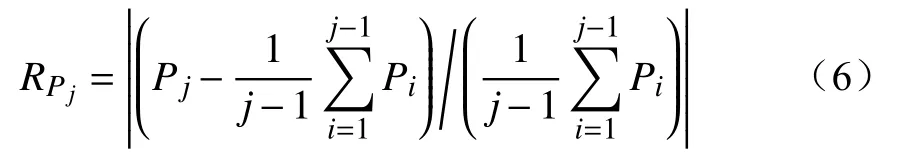
当RPj> 1时,前j−1个IMF分量作为伪分量,从原始信号中剔除,对剩余分量再进行EMD分解和重构,得到所有降噪后的IMF分量。
3 改进WNN故障诊断方法
3.1 WNN
WNN由文献[20]在1997年提出,兼具小波分析优良的时频特性与小波神经网络的自学能力。本文采用目前使用较为广泛的紧致型结构构建3层小波神经网络,如图6所示。

图6 三层WNN结构Fig. 6 Structure of three-layer WNN
输入层节点个数、隐含层小波元以及输出节点个数分别为m,n,N。对小波神经网络进行前向计算,可得隐含层第i个小波神经元输入hi为

式中:xk为输入层第k个输入样本;ωki为输入层节点k与隐含层第i层之间的连接权值,隐含层中选用Mexihat小波基及其尺度函数作为小波神经元,输出层节点采用经典的Sigmoid函数。
经过小波元激励后,第i个隐含层小波元输出oi为
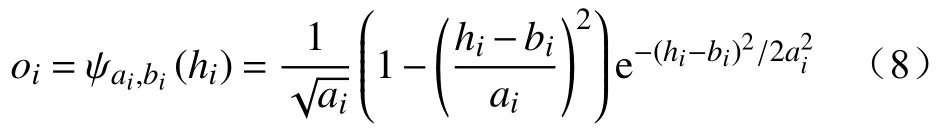
式中:ai和bi为隐含层第i层的伸缩平移系数。
由此可知输出层第j个节点输出yj为
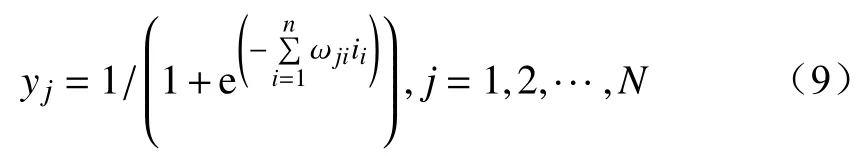
式中:ωji为隐含第i层与输出节点j之间连接权值。
WNN输出误差函数定位E为
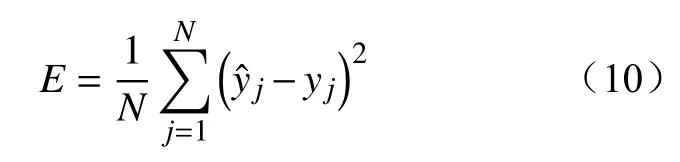
3.2 改进GA算法
传统GA算法过程主要包括精英选择、快速非支配排序、拥挤距离等概念[21]。精英选择算子直接决定种群优越性、多样性和收敛性。因此,本文主要通过对精英选择算子进行优化来提高GA性能。如在文献[22-23]中提出如下算子对其进行改进。

式中:Nm为非支配排序m等级中保留种群数量;N为种群大小;k为非支配排序等级总数。

从图7中不难发现,当选取r=0.75、k=10时,精英选择算子优化效果最佳。因此,选取r=0.75、k=10进行后续仿真。进一步可发现在各个等级中,种群个体选取数目均大于1/2,这有效保证了最优种群数量满足N的要求。而且种群个体选择概率与等级呈负相关,即等级越高,个体选择概率越低,这能有效提高新种群中的精英个体数量,进而提高收敛速度。

图7 不同等级个体选取概率Fig. 7 Probability of individual selection for different levels
3.3 基于改进 GA-WNN 的故障诊断方法流程
由于WNN对初始权值和阈值依赖性较高,若初始权值和阈值选取不当,可能无法收敛。由3.2节分析可知,GA算法通过全局搜寻,寻找最优种群,此时,将GA优化结果作为WNN初始权值和阈值,可有效提高输出精度和算法效率。由此可得改进GA-WNN小波神经网络在线智能诊断方法流程如图8所示。

图8 改进GA-WNN故障诊断方法流程Fig. 8 Flow chart of improved GA-WNN neural network intelligent diagnosis method
4 仿真分析
4.1 分合闸线圈电流特征值提取
以上海湘开电气有限公司的LHCKJ50-125 A/380 V真空断路器为实验对象,在实验室模拟不同故障下的分合闸线圈电流曲线特性,并提取分合闸线圈电流特征值。
4.1.1 不同故障下分合闸线圈电流曲线
通过2.2节中设计的实验室场景,对分合闸线圈进行模拟实验。图9为不同卡涩程度下分闸线圈电流,图10为不同电压异常情况下分闸线圈电流,图11为击穿状态下的分闸线圈电流。
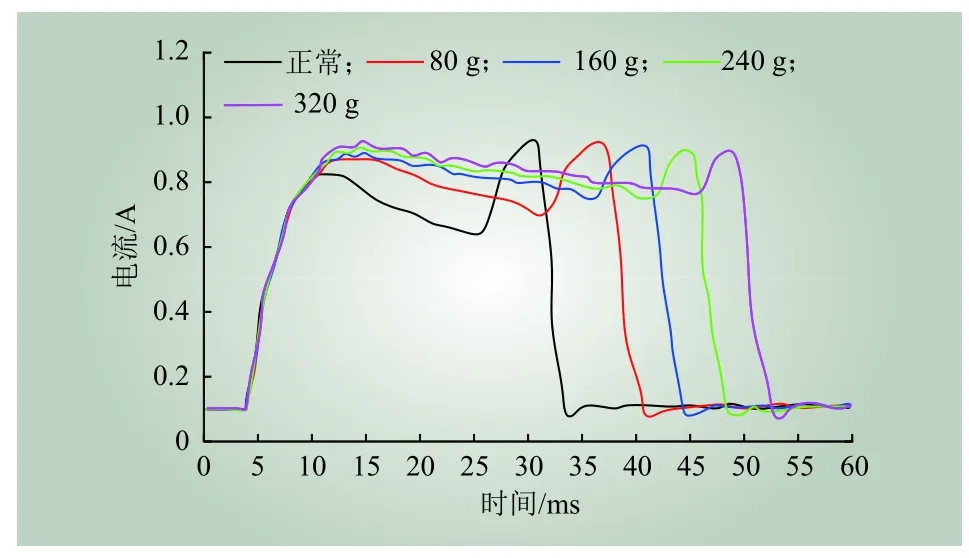
图9 不同卡涩程度下分闸线圈电流Fig. 9 Current of opening coil under different jamming degrees

图10 不同电压异常情况下分闸线圈电流Fig. 10 Current of opening coil under different abnormal voltages
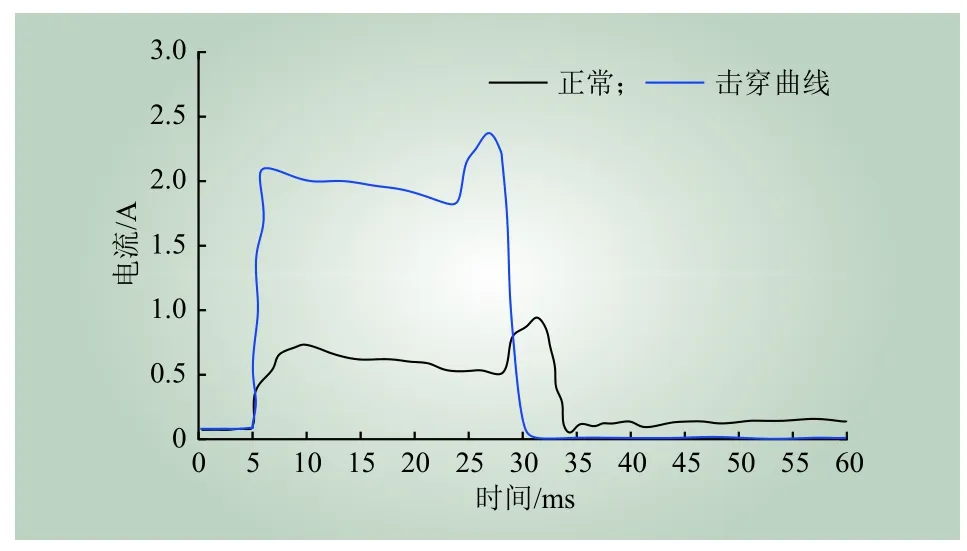
图11 为击穿状态下的分闸线圈电流Fig. 11 Current of opening coil under breakdown state
由图9可知,线圈电流随卡涩严重程度成正比,这是因为需要更大电磁力才能带动铁芯运动。而铁芯运动速度随卡涩严重程度增大而变慢,这是因为阻力的增大,电磁力受阻所致。由图10可知,线圈电流随电压升高而增大,铁芯运动时间越短。从图11中不难发现,击穿状态下的线圈电流幅值远大于正常电流幅值,持续时间短,且此现象与击穿破坏性程度有关。从上述3个模拟故障图形可知,该实验室模拟设计具有可行性,与实际工程情况相似。因此,将上述曲线作为后续仿真实验的基础数据,具有一定可信度。
1.1 资料来源 选取2015年1月-2017年4月佳木斯大学附属第一医院收治的80例NRDS患儿作为研究对象,将所有患儿依照入组时间编号,并采用随机信封法将患儿分为观察组及对照组,每组40例,两组患儿性别、胎龄、体质量、病情、分娩方式等一般临床资料比较,差异无统计学意义(均P>0.05),具有可比性。见表1。
4.1.2 分合闸线圈电流特征值提取结果
本节通过与EMD和小波变换进行对比来说明本文所提IEMD方法的有效性。其中,图12为原始信号曲线,图13为EMD方法分解结果,图14为小波变换分解结果,图15为IEMD方法去噪信号曲线,图16为IEMD方法分解结果,表1为特征值提取结果。
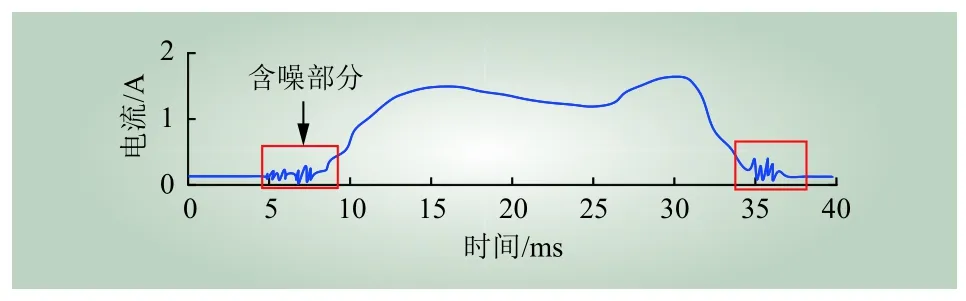
图12 原始信号曲线Fig. 12 Original signal curve
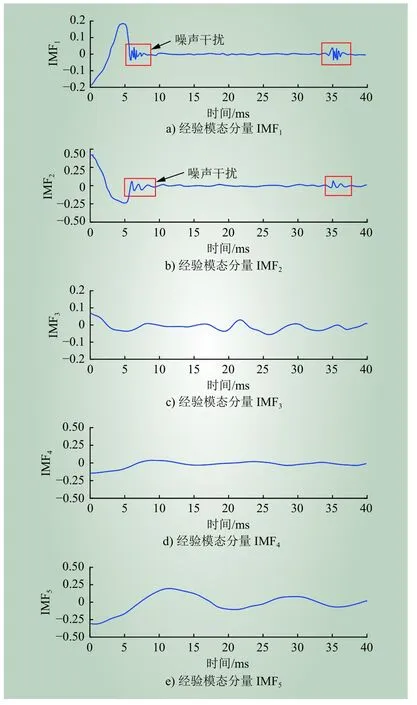
图13 EMD方法分解结果Fig. 13 Decomposition results of EMD method
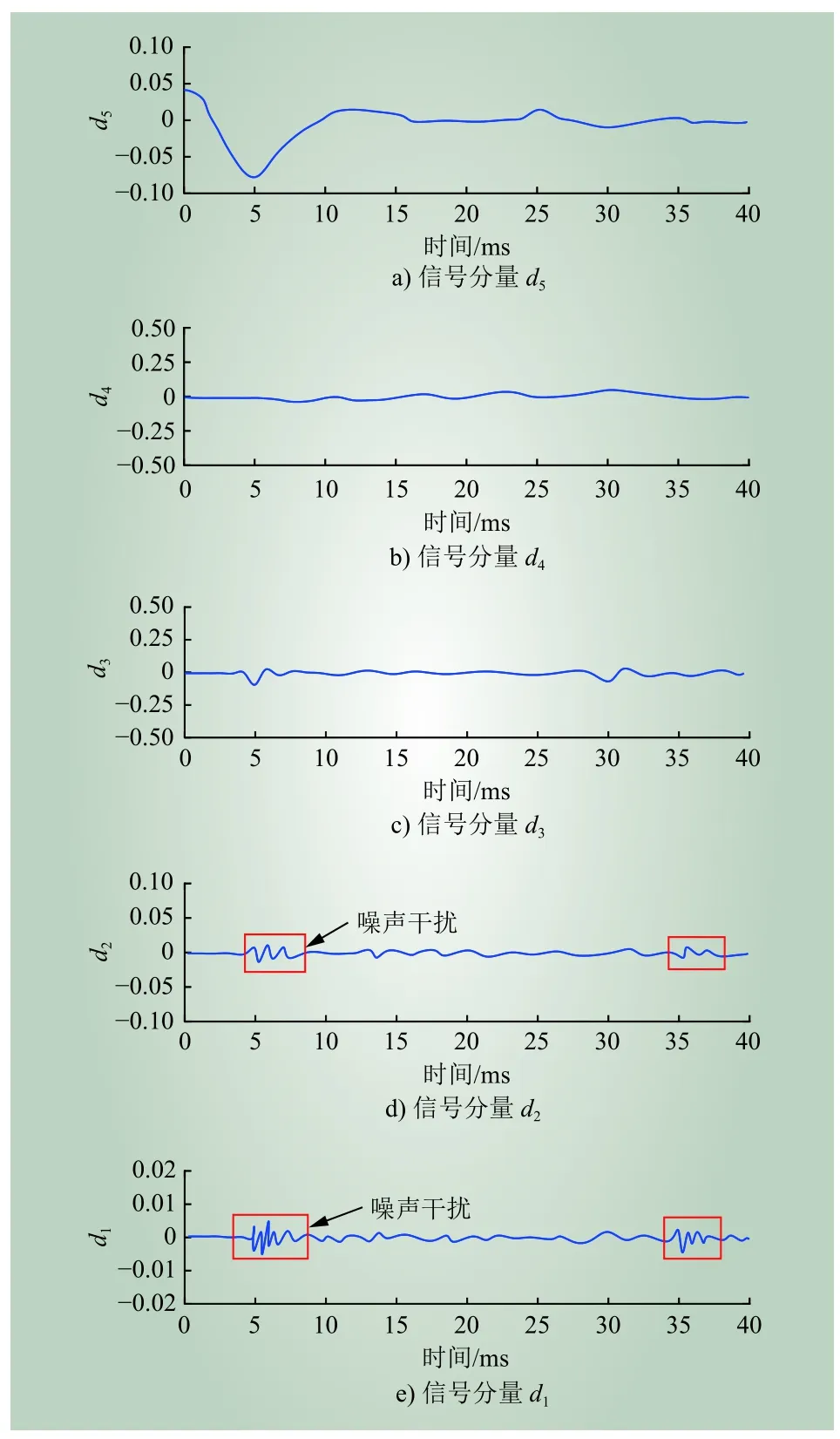
图14 小波变换分解结果Fig. 14 Decomposition results of wavelet transform
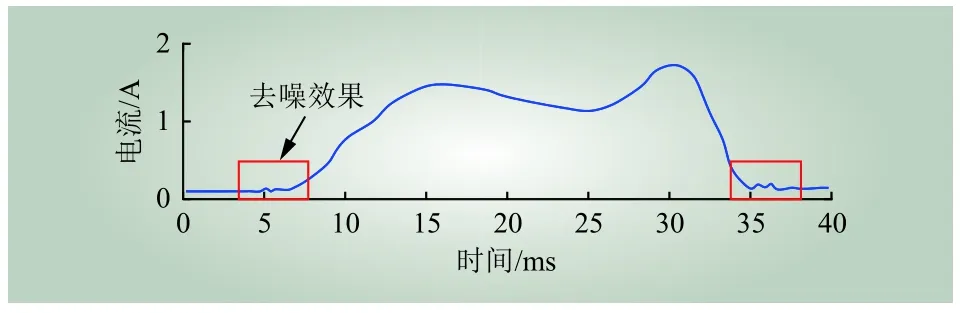
图15 IEMD方法去噪信号曲线Fig. 15 Denoising signal curve of IEMD method
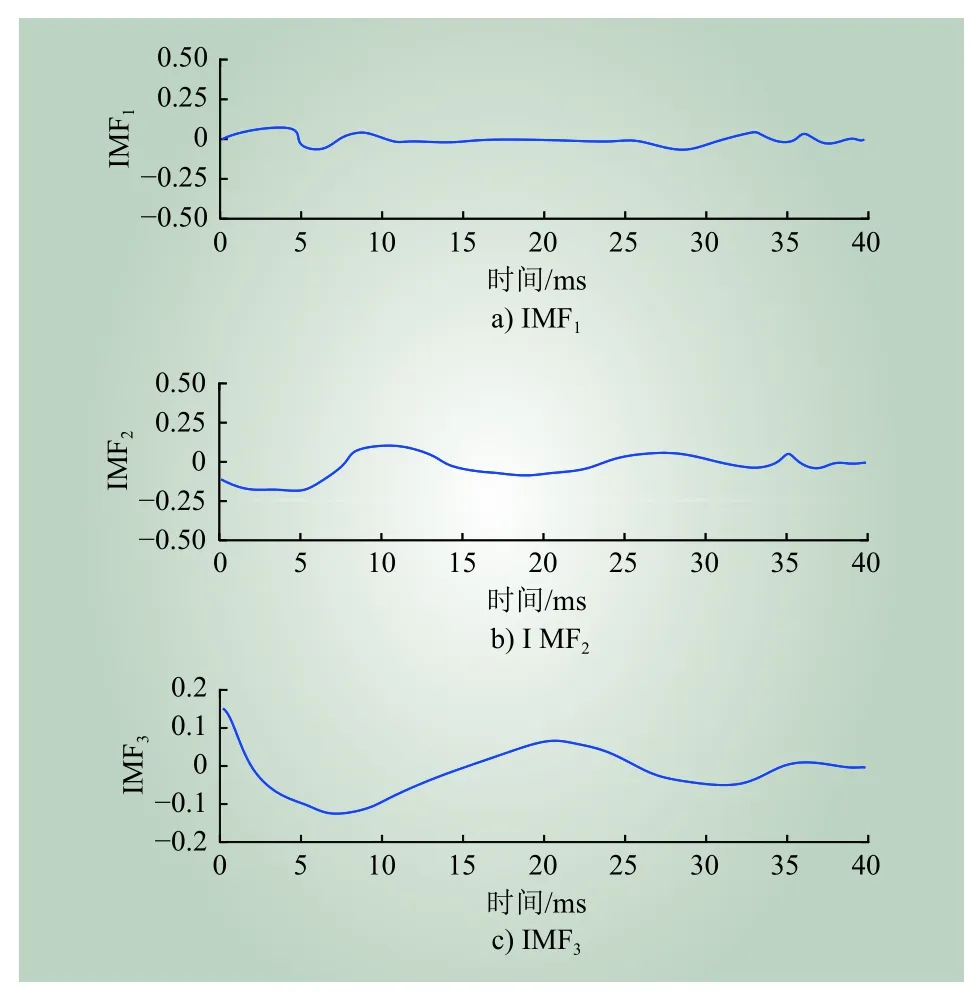
图16 IEMD方法分解结果Fig. 16 Decomposition results of IEMD method

表1 不同分解方法特征值提取结果Table 1 Extraction results of eigenvalues of different decomposition methods
从图13可知 EMD分解后,得到5个IMF分量,其中IMF1和IMF2含有大量谐波,来自原始信号中的噪声干扰,IMF3为高频分量,IMF4和IMF5为低频分量。d1~d5分别是高频到低频的信号分量,由于小波变换方法本身具有降噪重构功能,因此各分量中谐波含量较低。而本文所提IEMD方法,在传统EMD方法中添加降噪重构功能,因此在分解前削弱了幅度较大的噪声干扰波形,且效果明显。当信号再经IEMD分解后,只分解出3个IMF分量,且分解后不存在谐波分量。综上,本文所提的IEMD方法能有效分解信号,并保持原始信号不失真,准确性最高。
由表1特征值提取结果,不难看出,相比小波变换和EMD分解方法,利用IEMD算法提取的特征值误差较小,范围在0~0.3 ms内。而EMD分解方法误差最大,这主要是因为在使用小波变换和IEMD方法进行信号分解时,都对源信号做了消噪处理,而EMD没有,因此,小波变换和IEMD算法比EMD更加准确和可靠,但小波变换需人为设置基波函数来消噪,具有一定的主观性,致使分解结果相较于IEMD算法稍差。
4.2 故障诊断识别分析
基于4.1节仿真基础,利用IEMD对t0/ms、t1/ms、t2/ms、t3/ms、t4/ms、I1/A、I2/A 和I3/A 这7个特征参数进行提取,并作为GA-WNN算法的输入量(识别样本集)和初始种群,将分合闸线圈铁心卡涩、电压过高、电压过低和击穿4种故障类型作为输出量(仿真中纵坐标用4至1分别代表4种故障类型)。设定每组故障类型电流信号采集50组,共200组信号,将提取的特征参数放在一个7列200行的表格中,训练样本占70%,验证样本占15%,测试样本占15%,隐含层的数目设置为24。trainlm为训练函数,tansig为传递函数,最大学习次数和学习率分别为100和0.01。而GA算法中将种群设为50,迭代次数200次,交叉概率和变异概率分别为0.3和0.1。通过Matlab软件平台仿真,图17和图18分别为GA-WNN和传统WNN训练误差曲线和训练结果的对比。表2和表3分别为不同分闸线圈故障类型识别率。
从图17和图18可知,改进后的GA-WNN算法对分闸线圈故障识别率明显高于WNN。这主要是由于WNN受初始权值和阈值影响,而本文所提方法通过GA优化之后,能有效提高WNN收敛速度和最优解。由图17 a)可知,在前12次迭代中,验证集误差曲线仅存在微小的误差增大,直到在12次迭代之后,误差曲线才迅速下降,到第24次迭代,网络性能达到最优,完成网络训练。然而,改进后的GA-WNN小波神经网络算法中,设定WNN网络参数不变,由图17 b)可知,当网络训练6次时,验证集误差曲线连续下降,达到网络性能要求,经过14次训练后,网络完成分类功能,具有高效性。说明改进后的GAWNN算法经过GA算法优化权值阈值后,避免WNN自身进行多次训练选择,加速了WNN收敛速度。
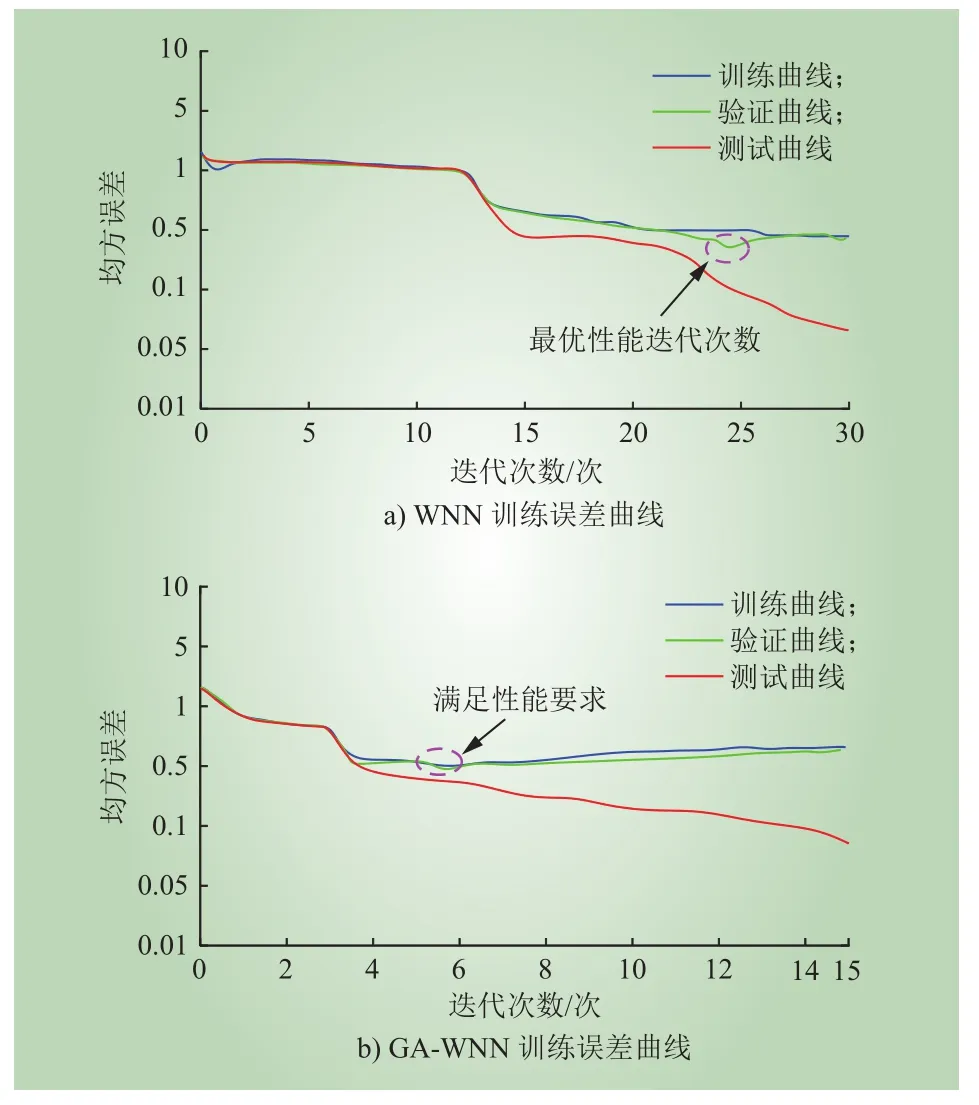
图17 训练误差曲线对比Fig. 17 Comparison of training error curves
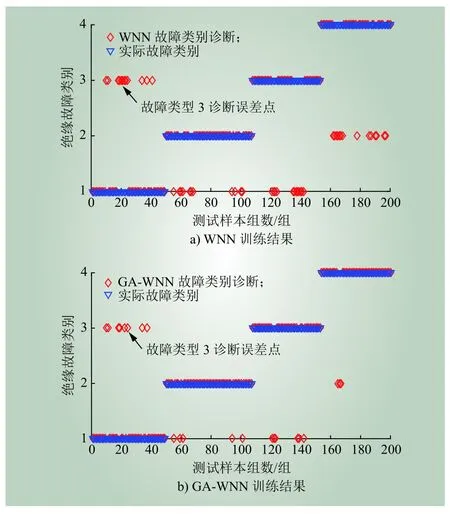
图18 训练结果对比Fig. 18 Comparison of training results
由表2和表3可知,基于WNN的分闸线圈故障平均识别率仅为81%,而基于GA-WNN分闸线圈故障平均识别率高达91%,且每类故障识别率均有所提高,其中线圈击穿故障识别率达到98%,与图18对应,图18中的故障诊断误差点是指诊断失败的解。这说明本文所提GA-WNN分合闸线圈诊断方法具备良好的诊断能力。

表2 WNN分闸线圈故障识别率Table 2 WNN opening coil fault recognition rate

表3 GA-WNN分闸线圈故障识别率Table 3 GA-WNN opening coil fault recognition rate
5 结论
基于真空断路器二次回路或操动机构运行状态能通过电流曲线特征值反映。根据信号经过EMD分解后IMF能量密度乘对应平均周期为恒定常数的性质,提出一种IEMD方法来提取分合闸线圈电流特征值,并在此基础上,利用改进GA对WNN参数进行寻优。通过仿真,得出如下结论。
(1)通过对真空断路器分合闸线圈不同故障进行实验室模拟,得到不同故障下的分合闸线圈电流曲线,并构建了故障特征曲线样本库,为后续故障辨别提高数据基础。
(2)提出的IEMD特征值提取方法,与EMD和小波变换方法相比,该方法能有效去除原始信号中的噪声信号和IMF伪分量,进而提高特征值提取准确率。
(3)针对WNN存在的参数难以确定的问题,提出改进GA对WNN参数进行优化。仿真结果表明,本文所采用的GA-WNN具有较好的学习能力以及较高的诊断精度,能够有效提升断路器故障诊断准确性,与传统WNN识别方法相比,GA-WNN故障诊断正确率高达91%,提高了10个百分点。
