南海北部陆坡海域第二模态内孤立波统计特征

许培鹏熊学军陈 亮宫庆龙郭延良于 龙吴 凡

(1.山东科技大学 测绘与空间信息学院,山东 青岛 266590;2.自然资源部 第一海洋研究所,山东 青岛 266061;3.青岛科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛 266237;4.自然资源部 海洋环境科学与数值模拟重点实验室,山东 青岛 266061;5.中国海洋大学 海洋与大气学院,山东 青岛 266100)

海洋内孤立波是发生在密度稳定层化的海洋内部的一种波动[1]。按照其垂向结构特征,可以将内孤立波分为n个模态。对于第i模态,其垂向位移在垂向上有i个极值点,即其振幅在垂向上有i-1次变化(i=1,2,3,…,n)[2]。在同等背景场条件下,第二模态内孤立波的振幅、流速及波速相比第一模态内孤立波较小。但其产生的强流发生的深度更深,这对于水下航行和水下施工可能产生更大的威胁。同时,根据目前的文献记载,第二模态内孤立波水平流的垂向切变最大可达到0.045 s-1,相当于典型第一模态内孤立波的2倍,这将会导致更强的垂向混合[3]。

以往的观测和理论研究大多聚焦于第一模态内孤立波,而对第二模态内孤立波的研究分析较为缺乏。近年来,关于南海第二模态内孤立波的观测报道开始出现。Yang等[4]基于潜标观测数据分析发现,南海北部陆坡上的第二模态内孤立波在夏季只是偶尔发生,而在冬季发生较为频繁。这是因为冬季跃层深度变深有利于第二模态内孤立波激发产生[5]。Ramp等[6]在2011年8月5日至16日的两次南海现场随船观测中发现多个第二模态内孤立波,其观测结果表明,第二模态内孤立波保持长距离传播,不是一种能穿越南海海盆的波动现象。Chen等[7]基于潜标观测周年数据对南海西北部海域第二模态内孤立波研究发现,其非线性特征可很好地用Kd V 方程进行描述,同时观测到有文献记载以来最强第二模态内孤立波。范文豪等[8]则利用地震海洋学方法对第二模态内孤立波波群进行了研究。目前,关于第二模态内孤立波生成机制的说法大致可以分为两类:一类是第一模态内孤立波与海底突变地形相互作用容易激发产生第二模态内孤立波[9-13];另一类是由于内潮、中尺度涡等海洋现象引起层结变化导致产生第二模态内孤立波[14-17]。例如:Vlasenko和Hutter[10]基于实验室试验结果研究发现,当第一模态内孤立波经过海底小山时会分裂形成第一模态和第二模态两种内孤立波;Lamb和Warn-Varnas[13]基于二维数值模拟研究结果表明,第一模态内孤立波在陆坡上传播过程中,上凸型和下凹型第二模态内孤立波均有可能产生;Dong等[16]基于SAR 影像资料研究表明,中尺度涡的发生改变了水体层化条件,为内潮的产生提供了便利的水文条件,当第一模态内潮与气旋涡发生共振时会激发产生第二模态内孤立波。

然而,基于现场观测资料的第二模态内孤立波研究还是相对较少。本文将基于布放在南海东沙群岛西侧陆坡海域的潜标周年观测数据,对第二模态内孤立波的振幅、波速、转向深度及流速流向等要素进行系统性统计分析。

1 数据与方法

1.1 数据资料介绍

1.1.1 潜标观测数据

观测数据来源为2020 年4 月1 日 至2021年5月7日在南海北部陆架坡折区域布放的一套锚系潜标。潜标布放位置为(115°48′00″E,20°48′00″N),布放站位水深约330 m(图1)。

图1 潜标布放位置及周边海域地形Fig.1 Mooring location and surrounding topographic features

该潜标为全剖面观测潜标,测量系统主要采用4种观测仪器:美国TRDI公司生产的型号为WHLR-150 型150 k Hz ADCP(Acoustic Doppler Current Profiler)和WHS-300型300 k Hz ADCP、加拿大RBR公司生产的concerto3温盐深测量仪(Conductivity Temperature Depth,CTD)以及美国SeaBird公司生产的SBE56温度测量仪(Temperature Logger,T)。潜标设备信息见表1,该潜标系统一共包含17台CTD、16台T、1 台300 k Hz ADCP、1 台150 k ADCP、1台1 MHz ADCP。温盐链深度范围为20～320 m,采用的是CTD 和T 交替式安装,垂向间隔为10 m;水深20～100 m 的海水流速剖面数据采集采用300 k Hz ADCP,采样间隔设为4 m;水深100～320 m 的海水流速剖面数据采集采用150 k Hz ADCP,采样分层间隔设为4 m。温盐观测的采样时间间隔为30或10 s,海流观测的采样时间间隔为2 min。

表1 潜标设备信息Table 1 Mooring equipment information

1.1.2 World Ocean Atlas 2013(WOA13)数据

由于潜标在海面至20 m 水深部分无温度和盐度观测数据,而实际计算需要完整的温盐剖面,故采用WOA13月均温盐剖面数据对全剖面数据进行补齐。WOA13数据由美国国家海洋数据中心(National Oceanographic Data Center,NODC)发布,包括年平均、季平均与月平均三种类型,水平分辨率为0.25°,垂直分辨率在0～100 m 处为5 m[18]。

1.2 数据分析方法

1.2.1 振幅计算

第二模态内孤立波存在上凸振幅和下凹振幅,本文将上凸振幅定义为正值,下凹振幅定义为负值。振幅计算过程如下:①确定极性。采用某一等温线第二模态内孤立波初始时刻深度ηst,与中间时刻深度ηmid进行比对,若则为下凹,若则为上凸。②确定振幅。计算该温度等值线在内孤立波发生时刻位移ηISW:

1.2.2 波速计算

根据Korteweg-de Vries(Kd V)方程[19],内孤立波波速(非线性波速)Cp为:

式中:Ca为线性波速,Cnon为非线性项。

保证率z计算：z=（Rn-R标）/Sn=（28.5-25）/0.97=3.61式中：Rn——n组试件强度的平均值，MPa；

Ca可以通过求解Taylor-Goldstein方程[20-21]得到:

式中:Ua为背景剪切流的流速,此处采用内孤立波开始时刻的前30 min内每一层流速的平均值;f2为内波垂向位移的模态函数;H为水深;N2为垂向浮力频率,在实际计算中可利用潜标温盐数据计算,其上层缺测部分采用WOA 数据进行补齐,计算公式为:

式中:g为重力加速度,ρ为海水密度。

非线性项Cnon为:

式中:η0为内孤立波最大振幅,α为非线性系数。α可由下式计算得到:

1.2.3 内波流流速与流向计算

内波流流速可根据以下公式计算得到[7]:

式中:uISW、vISW、wISW分别为去除背景流后的内波流东西向、南北向、垂向流速分量;u、v、w分别为现场实测流的东西向、南北向、垂向分量;u0、v0、w0分别为内孤立波开始时刻前30 min内的东西向、南北向、垂向流速分量的平均值;w c为ADCP自身起伏速度,采用与其一起固定在浮体上的CTD 水深数据计算获得。

内波流流向dirISW由去除背景流后的uISW、vISW计算得到:

式中:当uISW＞0且vISW＞0时,i取0;当uISW＞0且vISW＜0时或当uISW＜0且vISW＜0时,i取1;当uISW＜0且vISW＞0时,i取2。

2 统计结果与特征分析

2.1 第二模态内孤立波结构特征与发生频次

图2为2020年12月31日观测到的一个典型第二模态内孤立波的特征分布(图2a～图2d中对应红色虚线框内部分)。由其温盐结构(图2a)可以看出,其振幅存在2个极值点,其中180 m 水深以上振幅向上,最大振幅为51.1 m;180 m 水深以下振幅向下,最大振幅为76.1 m。图2b、图2c和图2d分别为其东西向、南北向及垂向内波流流速剖面。水平内波流流速剖面呈现明显的三层结构,上层和下层流向为东南向,中层流向为西北向,上层转向深度为106 m,下层转向深度为263 m。其垂向内波流流速也存在明显结构特征,180 m 水深以上,波峰之前为上升流,波峰之后为下降流;180 m 水深以下,波峰之前为下降流,波峰之后为上升流。根据Chen等[7]对第二模态内孤立波的研究,这些显著特征均说明该内波信号为第二模态内孤立波。

由根据东西向内波流与垂向内波流绘制的海流矢量特征图(图2e)可以看出,180 m 水深以上水层内波流呈“顺时针涡旋”;180 m 水深以下水层内波流呈“逆时针涡旋”。且两“涡旋”涡轴与波锋线平行。

图2 2020年12月31日观测到的一个典型第二模态内孤立波温度、流速及流速联合矢量剖面Fig.2 Vertical profiles of temperature-salinity,velocity,and velocity vector of a typical mode-2 solitary wave observed on December 31,2020

该站位共观测到72 个第二模态内孤立波,其中含第二模态内孤立波孤立子共101 个。将其与Chen等[7]2016年4月至2017年3月第二模态内孤立波的发生频次进行对比(图3),二者在各月份变化趋势相似。由图3可以看出,第二模态内孤立波在冬季发生频次较高,在夏季偶尔发生,这与Yang等[4]的观测结果一致。

图3 第二模态内孤立波月发生频次逐月分布对比Fig.3 Monthly frequency distribution of mode-2 solitary waves

2.2 振幅统计特征

图4为观测到的所有第二模态内孤立波的振幅分布情况,由图4可见,在观测的101个第二模态内孤立波中,最大振幅为下凹振幅的内波占比较大,约79.2%,说明大多数第二模态内孤立波的最大振幅为下凹振幅。从其平均振幅来看,上凸振幅的平均值为(23.5±10.0)m,下凹振幅的平均值为-(30.0±12.3)m,可见下凹振幅比上凸振幅大。总体来看,观测海域第二模态内孤立波的最大振幅是下凹振幅,为76.3 m,平均振幅为31.1 m(表2)。

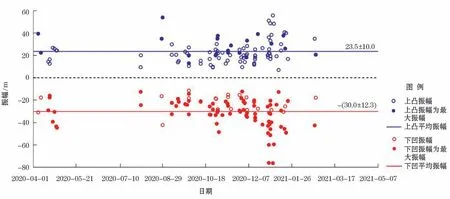
图4 上凸振幅与下凹振幅分布及各平均振幅Fig.4 Amplitudes of the convex and concave solitary waves and their mean values

表2 观测期间振幅统计Table 2 Amplitude statistics during the observation period

2.3 波速统计特征

由利用式(2)计算得到的第二模态内孤立波非线性波速分布(图5)可以看出,第二模态内孤立波的传播速度呈明显的季节性变化,夏季传播速度较快,冬季传播速度较慢,这是因为夏季海水层结较强,非线性作用对内孤立波波速的贡献率增大,而冬季海水层结较弱,非线性作用对内孤立波波速贡献率减小[2]。最大波速为0.67 m·s-1,发生在9月28日。其季节变化过程可以采用三角函数进行表达,如图5中黑色曲线所示,其相关系数为0.72,这一结果与Chen等[7]的结果接近。表3为其非线性波速与线性波速均值与最大值统计结果,从表中可以看出,非线性波速与线性波速均值相差0.01 m·s-1,最大值相差0.02 m·s-1。

图5 非线性波速变化分布图Fig.5 Variation of wave velocity

表3 观测期间非线性波速与线性波速均值、最大值统计结果Table 3 Statistics of the average and the maximum values of nonlinear wave velocity and linear wave velocity during the observation period

2.4 转向深度、流速流向统计特征

由图2可见,第二模态内孤立波为上、中、下三层结构,在3层结构中存在2个转向点。为了更好地了解该海域第二模态内孤立波在整个水层的分布情况,对观测到的第二模态内孤立波转向深度进行统计。

图6为第二模态内孤立波上层、下层转向深度与中层最大流速深度统计结果。可以看出,上层转向深度(图6a)在60～140 m,平均值为97.7 m,夏季转向深度略高于平均值,冬季转向深度略低于平均值。在对101个第二模态内孤立波全水深最大流速深度统计时发现,有83个最大流速发生在中层,占82.2%。据此我们可以认为第二模态最大流速基本都发生在中层。从图6b可以看出,中层最大流速深度在60～220 m,平均值约为134.6 m,分布较为均匀,无明显季节变化。下层转向深度(图6c)在140～270 m,平均值约为204.2 m,分布较为均匀。

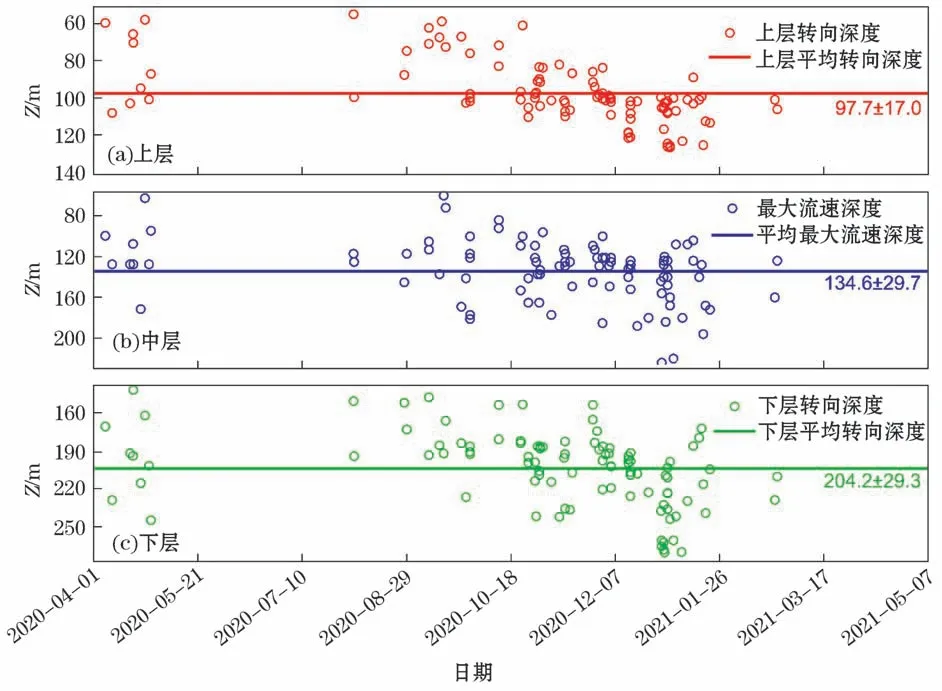
图6 第二模态内孤立波上下层转向深度、平均转向深度及中层最大流速深度、平均最大流速深度分布Fig.6 Distribution of upper and lower turning depth,middle layer maximum velocity depth,and their mean values

根据统计结果可知,该海域第二模态内孤立波上、中、下三层结构的两条分界线在其平均值附近波动,且其最大流速深度变化不大。在实际工程中,可根据该海域第二模态内孤立波的特征,在水下施工时采取有针对性的保护措施。

图7给出了第二模态内孤立波上、中、下三层最大内波流的流速(Vmax)、流向联合概率分布情况。可以看出,第二模态内孤立波的上层和下层最大内波流主要以SE 和SSE 为主,中层最大内波流主要为NW、NNW 向。从流速分布来看,中层内波流最大,流速主要分布于0.2～0.8 m·s-1区间范围内,占93.1%;上层次之,流速主要分布于0～0.6 m·s-1区间范围内,占98.0%;下层最小,流速主要分布于0～0.4 m·s-1区间范围内,占94.1%。由于上层实测流受多种因素干扰,其背景流量值与第二模态内波上层内波流相当甚至更大,因此上层内波流在计算时可能存在更大的误差。

图7 各层最大内波流流速及传播方向玫瑰图Fig.7 Rose diagram of the maximum internal wave flow velocity and propagation direction of each layer

由观测期间第二模态内孤立波内波流与实测流最大流速和平均流速统计结果(表4)可知,上层与中层内波流最大值大于实测流,下层内波流小于实测流。

表4 观测期间内波流与实测流各层最大值与平均值Table 4 The maximum and average values of each layer of internal wave current and the measured current during the observation period

3 结论

本文基于南海北部陆坡海域2020年4月1日至2021年5月7日一套周年全剖面潜标观测数据,开展了海域第二模态内孤立波及其特征的分析研究,共发现72 个第二模态内孤立波,包含101 个第二模态内孤立波孤立子。分析结果表明:

1)该海域第二模态内孤立波多发生9月至翌年1月份,冬季相对多发,这与Chen等[7]和Yang等[4]观测结果相似。第二模态内孤立波形态以上凸型为主,本次观测中未发现凹型,其中79.2%的最大振幅为下凹振幅,最大振幅是下凹振幅,达76.3 m,平均振幅为31.1 m。

2)该海域第二模态内孤立波波速呈明显季节变化,夏季波速大,冬季波速小,变化过程可以用三角函数很好地表达,拟合结果与Chen等[7]非常相似,且非线性波速与线性波速相差不大,说明该海域第二模态内孤立波受非线性作用影响较小。

3)该海域第二模态内孤立波上层转向深度约为98 m,下层转向深度约为204 m;在发生第二模态内孤立波期间,最大流速多发生于中层,流速集中分布在0.2～0.8 m·s-1,主要传播方向为西北向,最大流速平均深度为134.6 m。

本文是在科学研究和实际工程应用相结合基础上开展的观测、数据分析及研究工作。关于南海北部这一内波高发区的第二模态内孤立波的相关研究结果有助于加深对这一海域内波的认识,对南海北部陆架坡折区这一重要海区的水下航行和水下施工活动具有重要的参考意义,并可为后人的进一步研究提供借鉴。