BP和RBF神经网络应用于海表温盐短期预测效果对比

2022-06-06李亚蒙丁军航孙宝楠官

海洋科学进展 2022年2期

李亚蒙丁军航孙宝楠官晟*

(1.青岛大学自动化学院,山东青岛 266071;2.自然资源部第一海洋研究所,山东青岛 266061;3.山东省工业控制技术重点实验室,山东青岛 266071;4.自然资源部海洋环境科学与数值模拟重点实验室,山东青岛 266061;5.山东省海洋环境科学与数值模拟重点实验室,山东青岛 266061;6.青岛海洋科学与技术试点国家实验室区域海洋动力学与数值模拟功能实验室,山东青岛 266237)

20世纪以来,在全球气候变暖趋势下,极端气候及灾害事件频发,海洋环境也变得愈加复杂。要准确掌握海洋环境变化的规律,进而增强人类认识海洋、开发海洋的能力,需要具备比以往更准确、更及时和更全面的观测手段。海洋观测浮标可利用其搭载的各类传感器和设备,测量包括温度和盐度等海洋及大气环境要素,并实时将观测数据回传岸基台站。海洋观测浮标具有长时间连续、定点观测能力,搭载传感器种类、数量较多,其观测方式与海洋环境变化特征相吻合,是海洋立体观测网络中重要的节点形式。对观测浮标获取数据的有效利用与深度分析,可为全球气候变化趋势研究、海洋灾害预警和人类海上作业等领域提供有效的数据支撑[1-3]。

海洋观测浮标获取的多参数数据可以帮助人们了解海洋环境历经的状态,但对于人类海上活动而言,更需要从已有数据中预测未来将发生的变化,由此产生了人们对海洋环境要素进行预测的需求。相对于长期预测而言,海洋环境要素的时间序列短期预测面临更多偶然因素干扰,实现精确预测难度更大,但短期预测的结果对海上工程作业在安全保障、方案选择和成本控制等方面具有很高的应用价值。

对于绝大多数由实际观测资料构成的动力系统,往往表现出非线性、非平稳性双重特征。即系统各要素非独立,存在耦合作用,同时观测资料的时间序列又表现出具有趋势或周期性变化特性。对于这些动力系统,通常利用统计预测理论和非线性预测理论开展预测,由于其对信号平稳性的假定,有可能导致预测水平低下[4]。也有研究[5]通过对数变换或差分变换将相应的过程平稳化,对能够寻找近似平稳信号分量的非平稳过程取得了不错的预测效果。越来越多的研究[6-12]将神经网络预报法应用于气象和水文等非线性预测领域。常见的神经网络预报法包括反向传播(Back Propagation,BP)神经网络、径向基函数(Radial Basis Function,RBF)神经网络和差分自回归移动平均模型(Autoregressive Integrated Moving Average model,ARIMA)等。相比之下,海洋动力学预报法需要大型计算机对流体力学微分方程进行长时间积分,所需计算成本和对研究者建模水平的要求都较高。而神经网络方法逼近能力强、收敛速度快,具有信息分布式存储和并行协同处理的特点[13],实现相对简单,在近年海水温、盐预报应用研究中更为普遍。

基于BP神经网络和随机森林算法的评估模型[14]可以用来精准估算近岸海域的海表盐度。高国栋等[15]基于RBF神经网络模型建立了海水盐度的预测方法,并证明了该模型相较于BP神经网络模型收敛速度更快、精度更高。建立基于机器学习的反演模型并利用遥感技术进行大尺度动态模拟[16],或利用卫星辅助数据建立BP神经网络预测模型[17]均能较为精确地预测海表盐度。王颖超等[17]利用BP神经网络方法预测的海表盐度以及土壤水分和海洋盐度(Soil Moisture and Ocean Salinity,SMOS)卫星提供的3个粗糙度模型给出了盐度产品与ARGO 浮标实测盐度的均方根误差(Root Mean Square Error,RMSE),分别为0.847、2.041、2.028和2.081。基于空间遥感数据,使用神经网络算法预测[18-19]或者将深度学习神经网络与数值估值器相结合[20]均能有效预测海表温度。YANG 等[18]使用长短期记忆(Long Short-Term Memory,LSTM)神经网络预测了渤海1 d的海表温度数据,支持向量机、支持向量回归模型、FC-LSTM 等算法的预测结果与遥感实测值的RMSE为0.076～0.399,预测精度为98.49%～99.58%,证明了所提出的神经网络预测方法可行,但也发现数据集空间分辨率越高,精确预测难度越大。

以往研究结果证明了多种神经网络预测技术能够有效应用于海表温、盐时间序列数据的预测工作。然而在这些研究中,未讨论不同训练时长和预测时长等因素对预测精度的影响,也没有讨论算法的多海域适用性等问题。基于上述情况,本文将利用BP和RBF两种神经网络方法开展研究,以期获得一种具有稳定预报准确率,并具有较广泛适用性的海表温、盐短期预报方法。

1 数据与方法

1.1 数据来源

本研究数据主要来自美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)组织实施的OceanSITES观测系统中PAPA 站(145°W,50°N)、Stratus站(85°W,20°S)、KEO 站(145°E,32°N)、WHOTS站(160°W,25°N)和JKEO 站(146°E,38°N)等多个浮标站位于2009—2012年的监测数据。这些数据包括0～300 m 深度的温度、0～200 m 深度的盐度和密度、表层海流、纬向和经向海流的声学多普勒剖面等,以及风速、气温、相对湿度和大气压等气象观测数据。本文采用Mat Lab软件及其机器学习工具箱进行短期预测方法研究。

1.2 实验方法

1.2.1 BP神经网络预测模型的构建

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最为广泛的神经网络。BP网络按结构分为输入层、隐藏层和输出层,如图1所示。

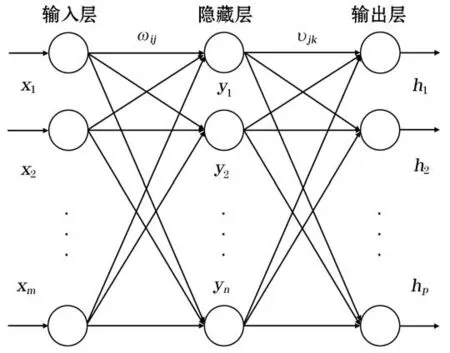
图1 BP神经网络结构Fig.1 Structure diagram of BP neural network

对于隐藏层,利用激活函数处理输入可以得到隐藏层输出,公式为:

式中,f(net j)为隐藏层激活函数,其中

对于输出层,利用激活函数处理隐藏层输出可以得到神经元输出,公式为:

式中,f(net k)为输出层激活函数,其中

BP 神经网络的优点是拥有很好的非线性映射能力和灵活的网络结构。网络各层的神经元个数可根据具体情况设定,并且其性能也会随着结构的差异而有所不同。但是BP神经网络也存在学习速度慢、因容易陷入局部极小值而无法得到全局最优值等主要缺陷。建立BP神经网络模型的步骤主要有5步[21]。

步骤一:读取研究对象数据集,如海表温度数据或海表盐度数据,对缺损值和突兀点进行预处理。

步骤二:划分训练集和测试集,对海表温度和海表盐度数据进行归一化处理。一般情况下,训练集的数据量会影响BP神经网络的预测效果。因此,以PAPA 站2009—2012年每年4月海表温度数据为样本,在预测时长固定为5 d的情况下,对比5 d、10 d、15 d、20 d和25 d不同时长训练海表温度数据集预测结果的均方误差,结果如表1所示。由表1可知,选取20 d的观测海表温度数据作为训练集,预测结果相对最优,训练时长也在可接受范围内。

表1 2009—2012年每年4月BP神经网络不同训练时长对应海表温度预测结果的均方误差Table 1 MSE of SST prediction results of different training time by BP neural network in April 2009—2012

步骤三:确定输入层节点和输出层节点数。实验中将历史海表温度和海表盐度数据作为输入,因此,选取输入层节点数为1,分别选择下一时刻的海表温度和海表盐度作为输出,因此,实验中输出层节点数为1。

步骤四:确定网络各层之间的传递函数和训练算法。BP神经网络使用最多的激活函数为sigmoid函数,其输入值可取任意值,输出值范围为0～1。本文选择隐藏层激活函数为tansig,其输入值为任意值,输出值为-1～1。选择输出层激活函数为purelin,其输入和输出值均为任意值。训练算法为Levenberg-Marquardt[trainlm],该算法作为系统的默认算法,其优势在于针对中等规模的BP神经网络,收敛速度最快。

通过网络测试,对比隐藏层节点数对应的训练集均方误差值,可以选择出最优的隐藏层节点个数,并应用于海洋数据预测。同样以2009—2012年每年4月海表温度的预测为例,设置每月前20 d海表温度数据为训练集进行实验,训练集均方误差结果如表2所示。由表2可知,最优的隐藏层节点数为8。

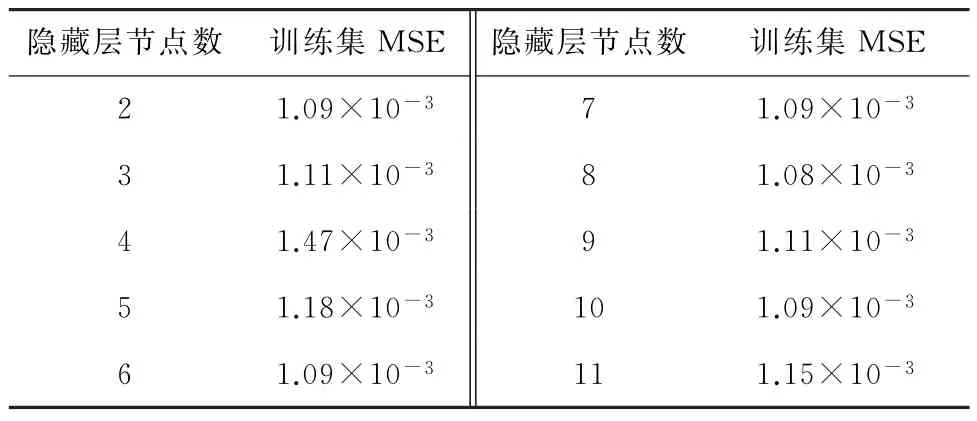
表2 BP神经网络隐藏层节点数对应海表温度训练集的均方误差Table 2 The MSE of SST training set corresponding to the number of hidden layer nodes of BP neural network

步骤五:分析BP 神经网络的预测值与实测值误差。通过误差分析,研究预测方法的适用性及策略改进。

1.2.2 RBF神经网络预测模型构建

径向基函数RBF神经网络主要用于解决多变量插值的问题。其取值依赖于空间任意一点x到中心点c的距离,即。最常用的径向基函数是高斯核函数[22],其形式为:

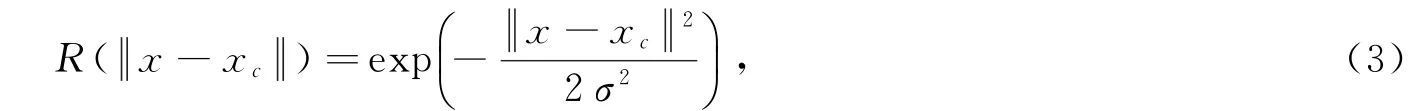
式中,x c是核函数中心,σ是函数的宽度参数。

RBF神经网络属于前向神经网络类型,拥有3层前向网络结构,包括输入层、隐藏层和输出层。输入层由信号源结点构成;隐藏层神经单元的激活函数是径向基函数,它是对应中心点径向对称且逐渐衰减的非线性函数,BP 神经网络可以有多个隐藏层,但是RBF 只有一个隐藏层;输出层对输入模式做出响应。从输入层到隐藏层的变换是非线性的,而从隐藏层到输出层的变换是线性的[23]。RBF神经网络结构如图2所示。

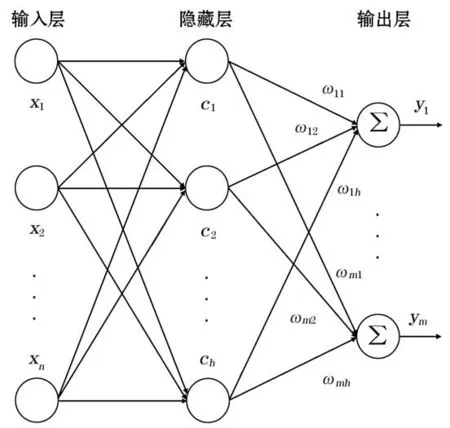
图2 RBF神经网络结构Fig.2 Structure diagram of RBF neural network

RBF神经网络实质上是利用由径向基函数构成的隐藏层,将输入变量直接映射至隐藏空间,通过确定RBF 中心点来控制映射关系。通常径向基函数对于空间中心点具备径向对称性,当神经元输入距离中心点较远时,神经元的激活程度较低,这属于RBF 神经网络的局部特性[24]。隐藏层的作用是将输入向量由低维度n映射成高维度h,使得向量具有线性可分的特性,通常利用高斯核函数作为激活函数:

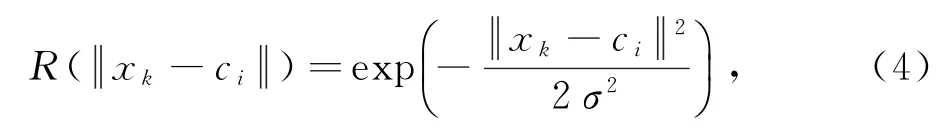
式中,k=1,2,…,n;i=1,2,…,h。

此时网络的输出是隐藏层输出的线性加权和,权即为可调参数,网络输出可表示为:

式中,k=1,2,…,n,j=1,2,…,m;σ为最小二乘损失函数,其中i=1,2,…,h;d j为理想输出值。

RBF神经网络的设计主要需要确认径向基函数中心、方差和隐藏层到输出层的权值三个参数。对于高斯核函数的径向基网络,首先利用k-means聚类得到h个中心,然后利用(式中,i=1,2,…,h,cmax表示选择的中心点之间最大距离)计算径向基函数方差,最后利用最小二乘法计算权值w,计算式为ω=

RBF模型建立步骤基本与BP神经网络类似。同样考虑到训练集的数据量对RBF 神经网络预测效果的影响,以2009—2012年间每年4月海表温度数据预测为例,在预测时长固定5 d情况下,设置不同训练时长进行对比,预测结果的均方误差如表3所示。由表3可知,选取20 d的海表温度作为训练集,预测结果相对最优。

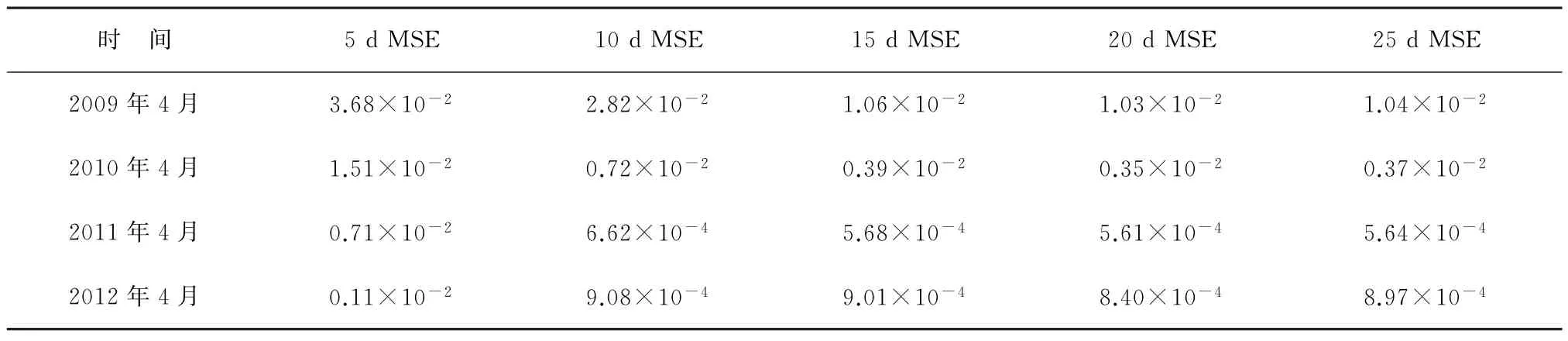
表3 RBF神经网络训练时间对应海表温度预测结果均方误差Table 3 Mean square error of SST prediction corresponding to different training days by RBF neural network

1.2.3 评价标准

本文采取均方误差(MSE)和平均绝对误差(Mean Absolute Error,MAE)两个指标来对检测结果进行分析。均方误差是指参数估计值与参数真值之差平方的期望值,可以评价数据的变化程度,MSE 值越小,说明预测模型描述的实验数据具有更好的精确度;平均绝对误差能更好地反映预测值误差的实际情况。2个指标的计算公式为:

式中,N为模型样本数,f i为海表温度或海表盐度的实测值,y i为海表温度或海表盐度的预测值。

相关系数是一种研究变量之间线性相关程度的量。相关系数以变量与各自平均的差值为基础,按积差的方式进行计算,其表达式为:处于0～1之间越接近1,代表预测值与实测值之间相关程度越高,即预测性能越好;r

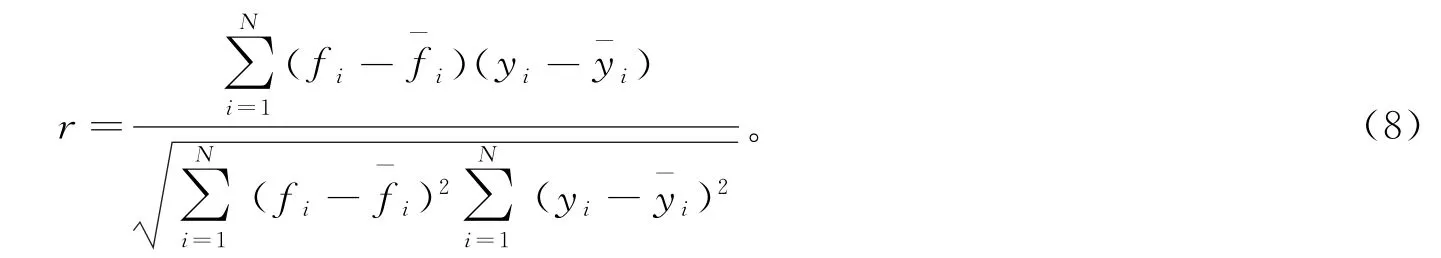
越接近0则代表预测性能越差。

2 结果与分析

海洋表面的海水温度、盐度等物理参数受到波浪、海流、风及海气交换等诸多不稳定因素的影响,有时变化剧烈、随机性较强,利用传统拟合、客观分析等方法难以进行准确的短期预测。

本文首先选择PAPA 站在2009年的1月、4月、7月和10月的海表温度和海表盐度数据作为研究数据集。1月、4月、7月和10月是常用的北半球冬季、春季、夏季、秋季四个季节典型环境特点代表月份。PAPA站浮标搭载传感器对海表温度及海表盐度采样周期均为1 h。根据前文所述,预测模型所用海表温度及海表盐度实测数据的训练集时间长度为20 d,短期预测时间长度为5 d,共25 d、合计600 h的海表温度及海表盐度数据变化曲线如图3和图4所示。

从图3和图4可见,海表温度数据表现出了明显的季节变化特征与日周期的变化特点,在这些趋势性和固定的周期变化基础上,叠加了非线性、随机的扰动。其中1月和10月海表温度呈明显下降趋势,分别从5.9 ℃下降到5.2 ℃、从11.0 ℃下降到9.0 ℃;4月和7月海表温度呈明显上升趋势,分别从7.0 ℃上升到9.0 ℃、从12.0 ℃上升到13.2 ℃。而海表盐度数据的季节性趋势相对不明显,整体变化范围较小,其中1月和4月大部分时间的海表盐度实测数据均超过32.50,而7月和10月大部分时间的海表盐度实测数据却均低于32.50。

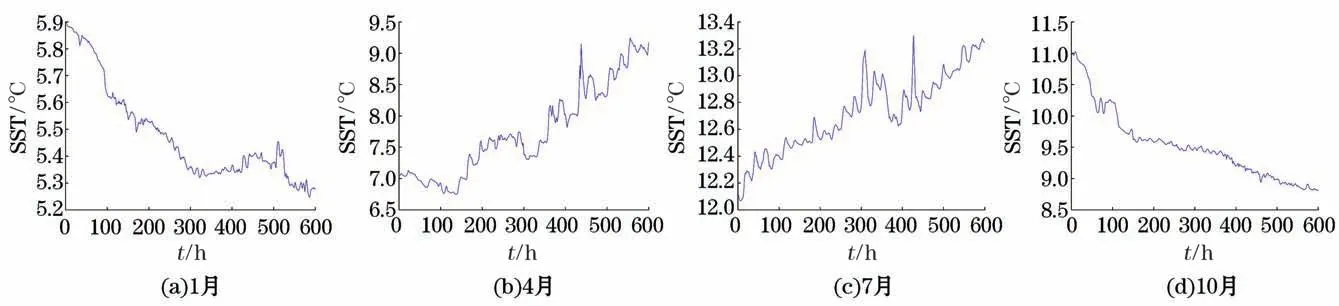
图3 冬、春、夏、秋四个季节海表温度随时间的变化Fig.3 Changes of SST with time in winter,spring,summer and autumn

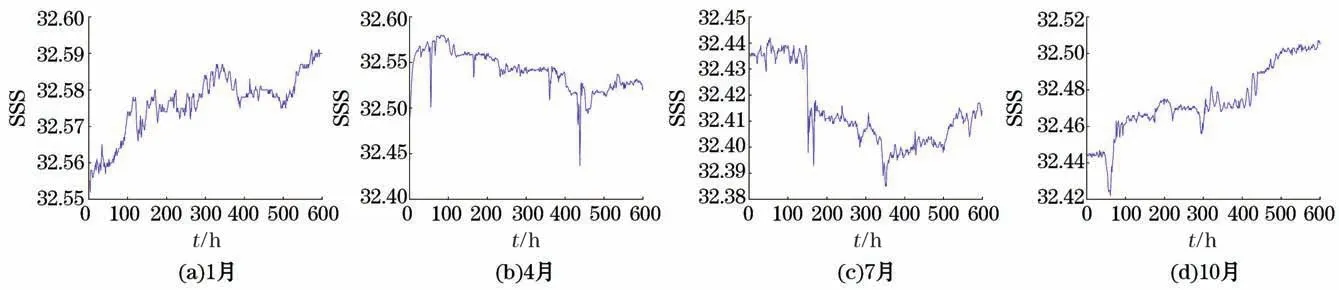
图4 冬、春、夏、秋四个季节海表盐度随时间的变化Fig.4 Changes of SSS with time in winter,spring,summer and autumn

2.1 预测对比实验

分别采用BP和RBF神经网络模型,对PAPA 站4个代表月份的21至25日、共120 h的海表温度与海表盐度进行了短期预报。预报结果如图5和图6所示。训练集均为各月前20 d的实测数据。BP神经网络隐藏层节点数为8,RBF神经网络隐藏层节点数为8。

从图5和图6看出,2种神经网络所获得的预测结果能够反映实测数据的变化趋势,对局部细节也有所反应。2种方法的预测效果随着预测时长增加均出现相对实测数据的偏离,其中BP神经网络的预测结果偏离更为显著。对2种方法预测结果的量化评价,主要从均方误差(MSE)和平均绝对误差(MAE)来衡量。

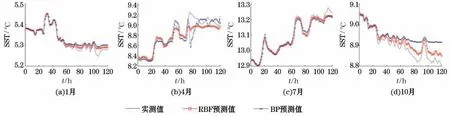
图5 4个季节代表月份21至25日海表温度预测结果Fig.5 Prediction results of SST from 21 to 25 in representative months of four seasons

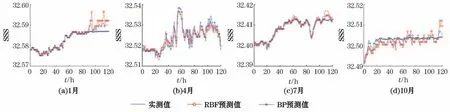
图6 4个季节代表月份21至25日海表盐度预测结果Fig.6 Prediction results of SSS from 21 to 25 in representative months of four seasons

在温度短期预报方面(表4),2种方法的MAE均远小于0.5 ℃。其中误差超过《海洋调查规范》[25]规定的0.02 ℃标准的情况,RBF预测结果有1次,BP预测结果有2次。由于盐度实测值(表4)较为稳定,各项误差指数均优于温度预报结果。其中误差超过《海洋调查规范》[25]规定的0.02标准的情况,只有BP预测结果有1次。RBF对海温和盐度的预测最小MAE分别为0.99×10-2℃和9.07×10-4,BP对海温和盐度的预测最小MAE分别为1.50×10-2℃和0.12×10-2。

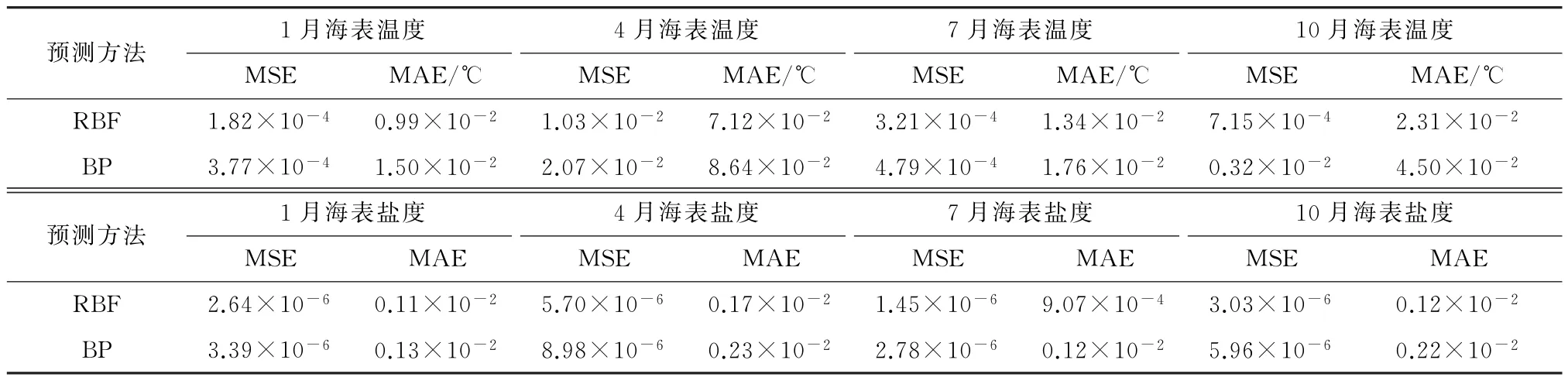
表4 2种预测方法预测海表温度和海表盐度误差分析Table 4 Error analysis of two methods for predicting SST and SSS

利用式(8)计算RBF和BP两种方法的预测结果与实测结果的相关系数,结果如表5和表6所示。从相关系数指标看,RBF预测方法对海表温度和海表盐度的预测结果,在所有月份均优于BP预测方法的结果。受篇幅所限,本文只展示了2种预测方法的温度(图7a)和盐度(图7b)单月预测结果的相关性趋势,其他3个月情况没有大的差异。在相关性趋势图中,RBF预测方法结果分布点也更集中于y=x直线,没有明显的偏离点。因此,就整体预测效果而言,RBF神经网络方法更精准。

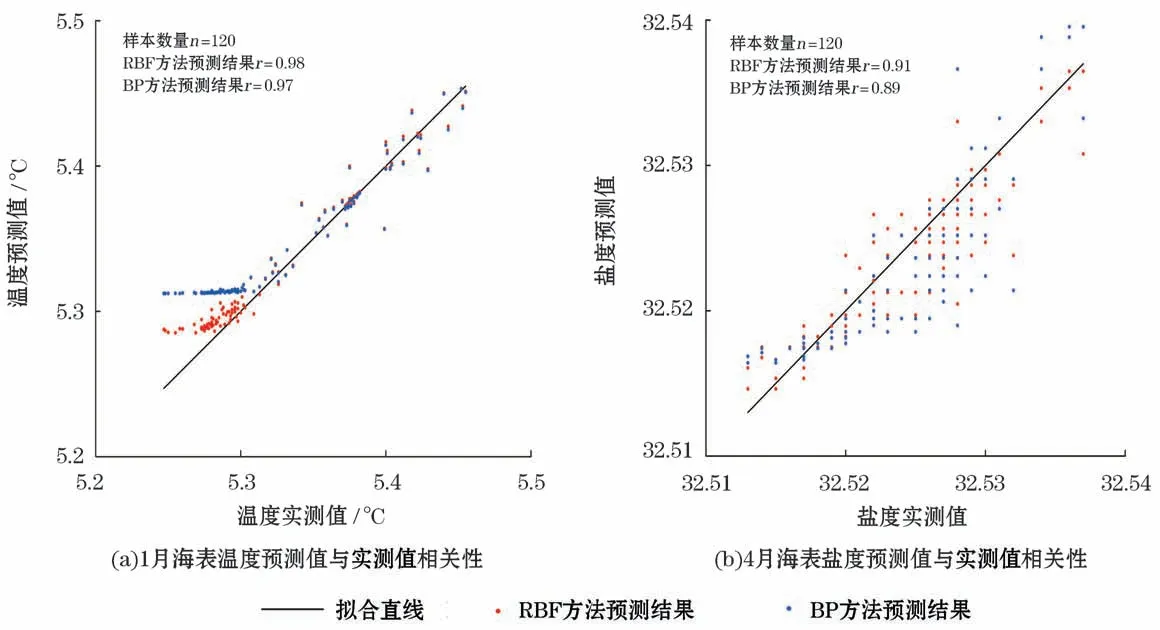
图7 RBF和BP两种神经网络方法1月海表温度、4月海表盐度预测值与实测值的相关性Fig.7 Correlation between the predicted and measured values of monthly SST or SSS by the two methods

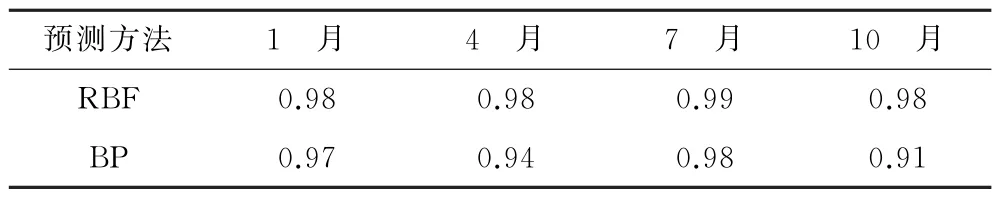
表5 2种预测方法的海表温度预测值与实测值相关系数Table 5 Correlation coefficients between predicted and measured SST of the two methods

表6 2种预测方法的海表盐度预测值与实测值相关系数Table 6 Correlation coefficients between predicted and measured SSS of the two methods

此外,对于不同季节的海表温度和海表盐度数据,2种神经网络方法预测效果的准确性均达到海表温度模式预报0.5 ℃的精度,海表温度和海表盐度的短期预报精度均接近《海洋调查规范》[25]规定的0.02 ℃和0.02标准的要求。预测结果的误差指标证明,这2种神经网络预测方法具备针对不同季节的海洋环境的适应能力,可以预测整年的海洋温盐数据。

5 d是典型的短期预报时长,但是在以20 d实测数据为训练集的前提下,对RBF和BP两种神经网络预测方法而言,对能获取更高预测准确率的最佳预测周期可开展进一步研究。

设置预测时长为1 d、2 d、3 d、4 d和5 d,利用2种神经网络模型对PAPA 站2009年各季节海表温度和海表盐度进行预测对比,训练集仍选最佳训练时长20 d。预测值各月MAE 的结果如图8 和图9所示。由图8和图9可知,随着测试集预测时长的变化,利用RBF神经网络方法预测的海表温度和海表盐度的MAE始终低于BP神经网络。由于海表温度的变化幅度大于海表盐度,因此随着预测时长的增加,海表温度预测的误差增加较为明显,除个别情形(如RBF 对7 月海表温度的预测)外,2 种预测模型的海表温度预测最佳周期可选为1 d;由于海表盐度的变化幅度较小,因此预测误差随预测时长的变化不太明显,整体趋势为随着预测时长增加,预测误差也对应增大,最佳预测周期可选2～3 d。在实际应用中,需综合考虑预测成本与准确性的实际需求确定预测时长。

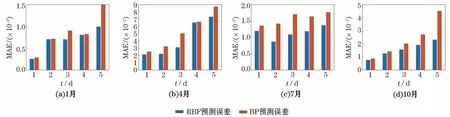
图8 RBF和BP两种神经网络预测方法在4个代表月份以不同预测时长预测海表温度结果的平均绝对误差Fig.8 The MAE of SST predicted by two prediction methods with different prediction days in four representative months

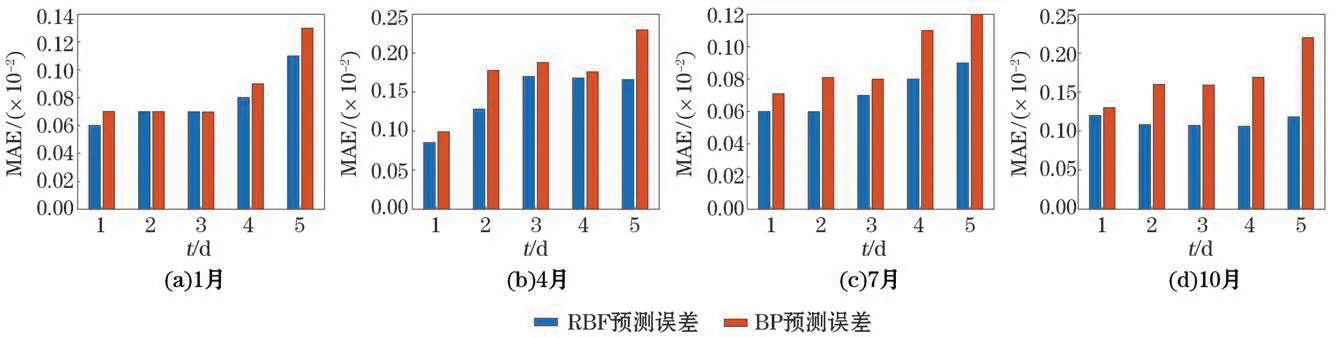
图9 RBF和BP两种神经网络预测方法在4个代表月份以不同预测时长预测海表盐度结果的平均绝对误差Fig.9 The MAE of SSS predicted by two prediction methods with different prediction days in four representative months

2.2 多站点预测验证

为了验证预测模型的适用性和普遍性,选择PAPA 站以外的其他4个站点的浮标数据,利用RBF神经网络模型对海表温盐数据进行预测验证。这4 个站点分别为Stratus站(85°W,20°S)、KEO 站(145°E,32°N)、WHOTS站(160°W,25°N)和JKEO 站(146°E,38°N)。各站点海表温度和海表盐度数据采样周期也为1 h,模型参数通过上述实验方法选定,海表温度预测时长为1 d,海表盐度预测时间为3 d。其中,利用位于东太平洋距离较近的KEO 站和JKEO 站对2010年的海表温度和海表盐度数据进行重复性实验,验证RBF神经网络模型预测能力的可重复性;利用中太平洋相距较远的WHOTS站和西太平洋Stratus站2012年的海表温度和海表盐度数据验证预测模型的普适性。由于数据较多,本文只给出Stratus站(85°W,20°S)各季节的预测结果(图10和图11)。各站点的预测误差及相关系数如表7～表10所示。

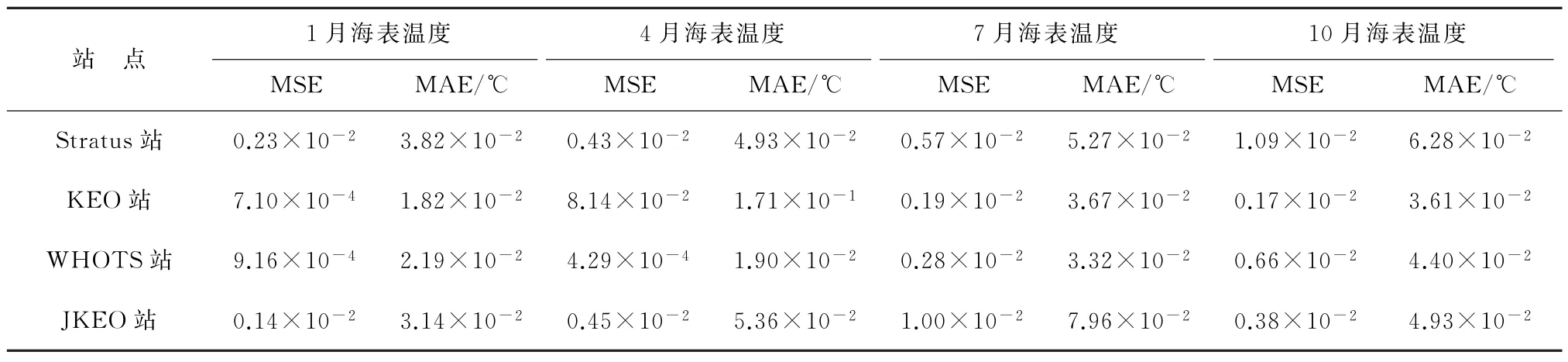
表7 RBF神经网络海表温度预测误差Table 7 Prediction error of SST by RBF neural network

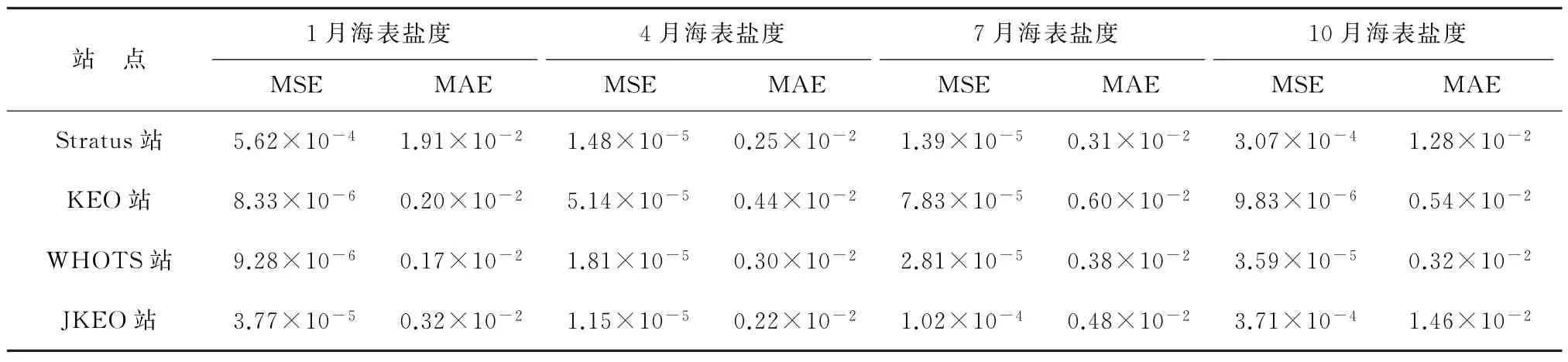
表8 RBF神经网络海表盐度预测误差Table 8 Prediction error of SSS by RBF neural network

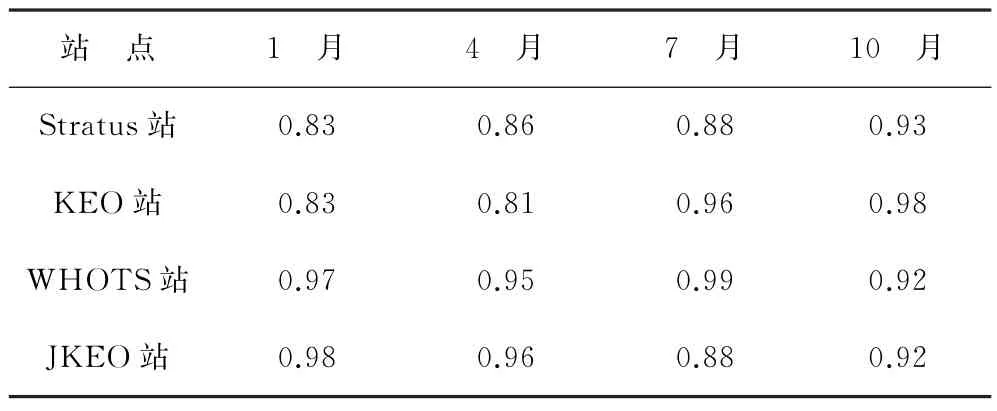
表9 RBF神经网络预测海表温度的预测值与实测值相关系数Table 9 Correlation coefficients between predicted and measured SST predicted by RBF neural network

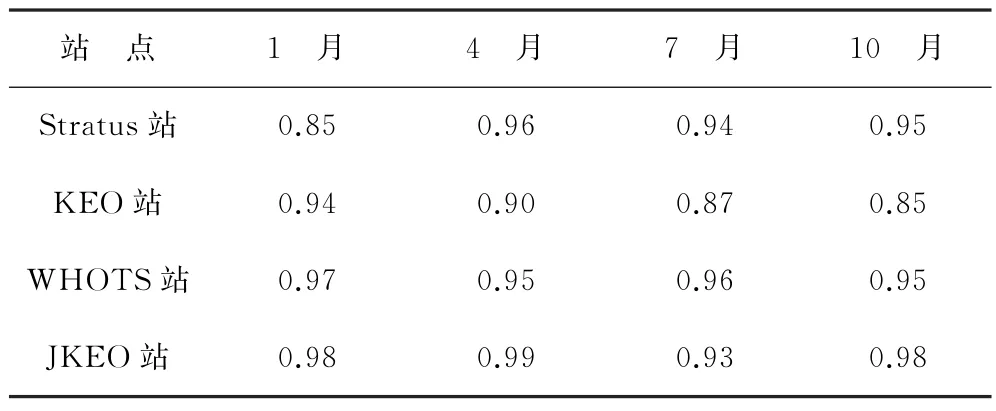
表10 RBF神经网络预测海表盐度的预测值与实测值相关系数Table 10 Correlation coefficients between predicted and measured SSS predicted by RBF neural network

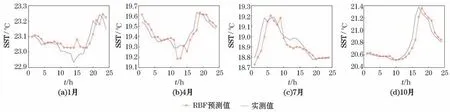
图10 Stratus站4个代表月份1 d海表温度预测结果Fig.10 1-day SST prediction results of four representative months at Stratus Station

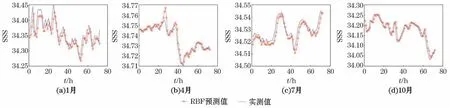
图11 Stratus站4个代表月份3 d海表盐度预测结果Fig.11 3-day SSS prediction results of four representative months at Stratus Station

由多站点预测实验结果的误差分析和相关系数比对可知,RBF神经网络模型对于海洋表面温盐数据的超短期预测具备普遍适用性,并能精确拟合出多个海域及其四季海表温盐数据的变化规律。这表明,尽管海表温盐等数据受诸多不稳定因素影响而具备随机性、非线性的特点,但使用RBF神经网络能够进行有效、高精度的预测。相较于已往研究成果,应用本方法对独立站位海表温度数据进行1 d预测、对海表盐度数据进行3 d预测,预测结果在均方误差和平均绝对误差指标方面,均优于已有的海表温度和海表盐度遥感数据预测研究所取得的结果。