基于均布式多孔表面吹气的索结构尾流控制

高东来，余海洋，陈文礼†

（1.土木工程智能防灾减灾工业与信息化部重点实验室（哈尔滨工业大学），黑龙江哈尔滨 150090；2.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），黑龙江哈尔滨 150090）

近年来，我国大跨度桥梁建设发展迅速，主跨千米级的桥梁不断建成.大跨度桥梁一般采用缆索承重体系，具体的结构形式为斜拉桥与悬索桥.与中小跨度桥梁相比，大跨度斜拉桥和悬索桥的柔度大，动力效应更明显.斜拉桥和悬索桥的桥址一般处于山谷、江河和沿海地区，风环境较为复杂.大跨度柔性桥梁为风敏感结构，在风作用下产生的效应十分明显，需对结构和构件的风效应进行评估［1］.在定常气流的作用下，结构或构件可能会由于气动弹性失稳而发生自激的、发散性的风致振动，如颤振和驰振；在脉动风的作用下，则可能发生限幅的强迫振动，如抖振.对于大跨度桥梁，一种更为常见的风致振动形式为涡激振动，该振动形式是由于钝体绕流时的旋涡脱落频率和结构自身振动的某阶频率相接近时发生的锁定现象而产生，在较低风速区间内发生，且振幅有限，介于发散的自激振动与限幅的强迫振动之间［2］.为保证大跨度桥梁的正常使用和承载能力，需对风致振动进行抑制，既可通过抑制结构或构件自身的振动，也可通过对绕流场的调控加以实现［3］.

索结构是大跨度桥梁重要的组成部分，如斜拉桥的拉索、悬索桥的主缆和吊杆，以及下承式、中承式拱桥的柔性吊杆等.以斜拉桥的拉索为例，其可能发生的振动形式为涡激振动、尾流驰振、风雨激振和参数共振等［2，4-5］.Chen 等［6］通过节段模型风洞试验对西堠门大桥吊杆的桥塔尾流致振现象进行了分析，建立了气动力模型和相应的吊杆运动方程.索的驰振和风雨激振的振幅过大，一般为几倍的拉索直径甚至更大，可能会影响行车安全；索发生涡激振动时的振幅一般不大，但发生频率最高，会使其耐久性受到影响，甚至会发生疲劳破坏.因此，控制并抑制大跨度桥梁索结构的风致振动具有十分重要的意义.

索结构振动的控制可分为结构措施、机械阻尼措施和气动措施［2］.结构措施一般是通过设置辅助索减小索的自由长度，增加索面刚度，以削弱振幅，其缺点是安装困难，且对桥梁的外观造型有影响.机械阻尼措施一般是在拉索与桥面间设置阻尼器，耗散振动的能量.常见的阻尼器有油阻尼器、剪切型黏滞阻尼器和磁流变阻尼器［7］等.气动措施是指改变结构或构件的横截面形式，改变外部气流的流动特性，以达到控制风致振动的目的.根据外部能量的消耗与否，流动控制方法可以分为主动控制与被动控制［8］.被动控制措施一般通过改变钝体的外形，以改善其流体动力学特性，从而对流动分离和尾流进行控制并抑制气动力，尤其是降低阻力和脉动升力.被动控制方法的主要优点是节省能量并易于安装［8］.常见的被动控制方法有表面设置凸起［9-10］、安装导流板［11］、开槽［12］等.然而，与主动控制相比，被动控制方法往往难以达到非常明显的控制效果，且无法对控制过程进行调节.

在主动流动控制方面，定常吸/吹气是一种常见的控制方法.Chen 等［13］通过风洞试验研究了在雷诺数Re为3×104时定常吸气的流动控制效果，需要指出的是，该雷诺数位于斜拉索通常发生涡激振动时的风速所对应的雷诺数区间.研究结果表明，尾流区的旋涡脱落过程发生了变化，作用于圆柱的不稳定气动力得到了削弱，从而抑制了圆柱的涡激振动.在控制过程中，吸气孔在圆柱表面的分布方位角是十分重要的控制参数.Gao 等［14］通过试验研究了圆柱在迎风侧吸气与背风侧吹气同时作用下的控制效果.结果表明，作用于圆柱上的阻力和气动力脉动幅值均有降低，旋涡脱落频率也发生了变化，后驻点的吹气在尾流中产生了一对旋涡，对原始的旋涡脱落过程有调节作用.

本文通过风洞试验，研究了具有均布式多孔表面的圆柱在定常吹气控制下的尾流特性，对尾流的流动特性如流线、湍动能、雷诺应力和涡量等进行了分析，并结合尾流区的频谱特性，得到了不同吹气控制程度下的尾流变化过程.

1 风洞试验概况

试验在哈尔滨工业大学大气边界层风洞与浪槽联合实验室1 号闭口回流式风洞（SMC-WT1）中进行.试验段的宽度和高度均为505 mm，长度为1 000 mm.试验段的壁面为透明玻璃，可保证良好的流动可视化观测条件.试验段风速在0～24 m/s 范围内连续可调，且上游位置所布置的蜂窝和栅格可保证试验段风速稳定，湍流度较小（约为0.30%）.试验的来流风速U∞设为3.0 m/s，对应的雷诺数Re为1.0×104.试验所用的多孔索结构模型如图1（a）所示，模型两端为具有光滑表面的空心有机玻璃管，中间段为多孔段，材料为树脂，采用3D 打印技术制作而成.模型的外部直径D为50 mm，内部空心段直径d为25 mm，展向长度L为504 mm，其中多孔段的长度L0为64 mm.模型多孔段的内部构造如图1（b）所示，沿模型环向均匀布置有30 个气孔，展向孔数为16 个.模型表面单个气孔直径为3.2 mm，气孔总面积Sh约为3 858 mm2.在本试验中同时研究了无控圆柱（光滑圆柱）作为对比.图1（c）所示为粒子图像测速（particle image velocimetry，PIV）系统的示意图，该系统主要由高能双脉冲激光器（Beamtech Vlite 430）、高分辨率双曝光CMOS（complementary oxide semiconduc⁃tor）相机（pco dimax HS4）、烟雾发生器（ROSCO Al⁃pha 900）和数字式延迟发生器（Berkeley Nucleonics Model 577）组成.试验所用的Nd：YAG 激光器所释放的激光能量为0.435 J，波长为532 nm，双路激光的时间间隔Δt为0.1 ms.CMOS 相机的采样频率为200 Hz，其与激光器之间的信号同步由数字式延迟发生器实现.示踪粒子为平均直径1～5 μm 的油滴，通过烟雾发生器均匀散布于试验段内.通过帧间互相关运算，可由相机采集到的图像计算得到对应时刻的速度场，并进一步计算得到尾流面内涡量（ωz=∂v/∂x-∂u/∂y）、湍动能和 雷 诺切应力等流动物理量.

图1 试验模型及PIV观测系统示意图Fig.1 Diagrams of the test model and the PIV measurement system

模型的主动吹气流动控制通过外部风机实现，风机与模型之间通过预留的气孔与PVC软管进行连接.风机的吹气流率Q通过流量控制器（Omega FMA-2613A）进行控制并保持恒定，流率范围为24～216 L/min，步长为48 L/min.本文引入了无量纲参数——等效吹气系数CQ对主动吹气流动控制进行量化，其定义为：

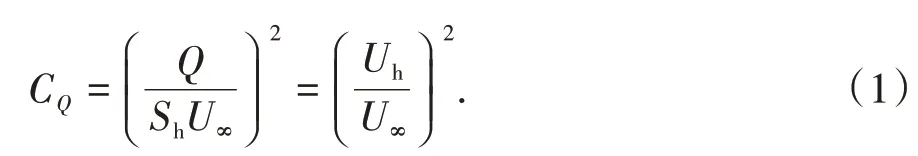
式中：Uh为表面气孔处平均吹气流速，m/s.在风洞试验中，各流率所对应的主动控制工况的吹气控制参数如表1所示.

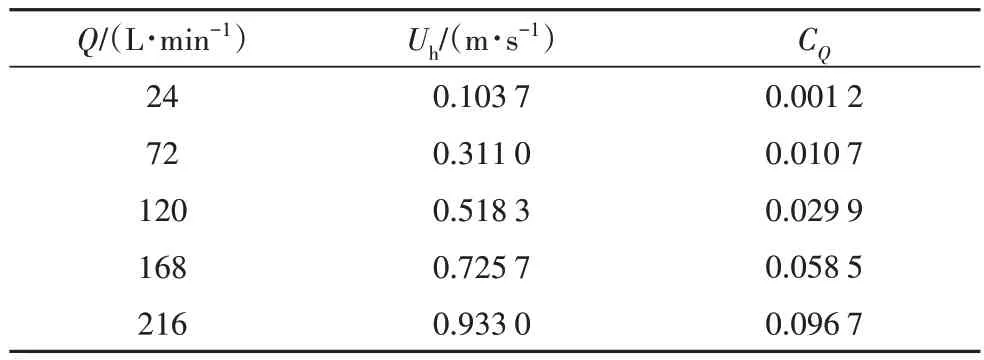
表1 试验模型的吹气控制参数Tab.1 Blowing control parameters for test cases in the present study

为分析流场中主要的拟序结构，本文采用了本征正交分解（proper orthogonal decomposition，POD）方法，将PIV 所观测到的原始流动物理量由前15 阶POD 模态进行重构，并分析了POD 前4 阶模态的特性.为进一步评估均布式多孔表面吹气对索结构的尾流控制效果，采用动态模态分解（dynamic mode de⁃composition，DMD）方法对一些典型工况尾流场主要模态的动力学特性进行对比分析.

2 结果与讨论

2.1 POD模态特性

模态能量是POD 模态排序的依据，低阶的POD模态能量占比最高，第j阶POD 模态的能量占比Pj定义为该阶模态的特征值λj与从流场中提取出的所有n阶模态的特征值之和的比值，即：

在本文中，共提取了前500 阶的POD 模态进行计算，即式（2）中n=500.前100 阶POD 模态的累积能量分布曲线如图2 所示，对于无控圆柱，低阶次模态的相应能量占比较大，且随阶次的增高而降低，即低阶次的POD模态代表整个流场中大尺度的拟序结构［8］.无控圆柱前4阶POD模态的累积能量占比约为流场总能量的75%，与Feng 等［15］的研究结果相似.从图2 中可看出，随着等效吹气系数CQ的增大，各工况的前100 阶POD 模态累积能量占比呈下降趋势，意味着索结构在均布式多孔表面吹气控制下，流场中大尺度的拟序结构得到了有效的抑制.同时，低阶次的模态能量相对降低，而高阶次的模态能量相对升高，表明流场中的拟序结构尺度趋于均一化.均布式多孔表面吹气控制使得前2 阶POD 模态能量降幅最为明显，由于第1、2 阶POD 模态对“2S”旋涡脱落模式中交替脱落的旋涡起控制作用［16］，由此可知吹气控制可有效控制索结构尾流中交替脱落的旋涡（即Karman 涡街），具体控制效果将在下文进行分析与讨论.

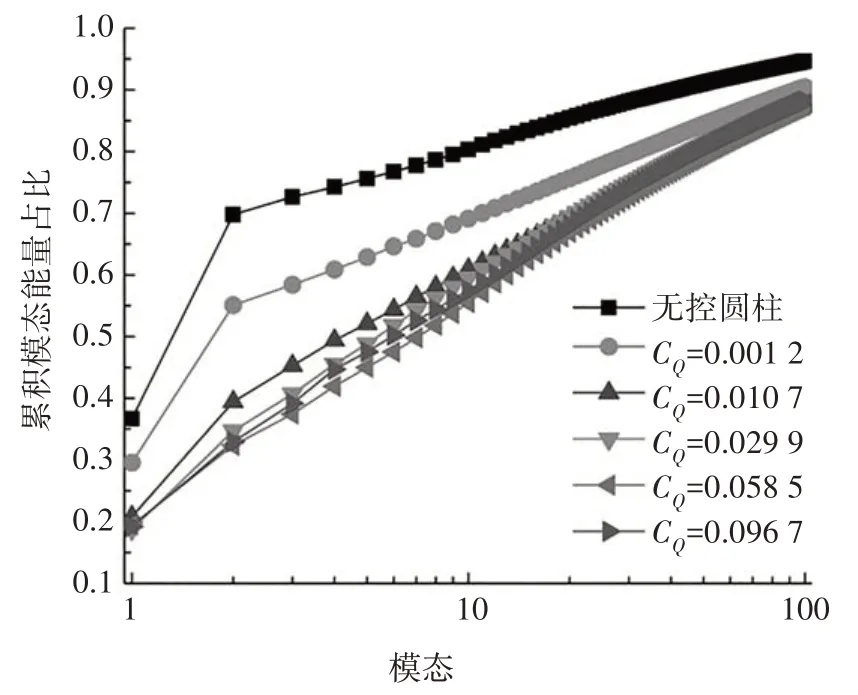
图2 前100阶POD模态累积能量分布Fig.2 Cumulative energy proportions of the first 100 POD modes

流场经POD 重构后的前4 阶模态涡量分布如图3所示.各工况的第1、2阶POD模态涡量沿圆柱中心线Y/D=0 呈对称分布，第3、4 阶模态则呈反对称分布.无控圆柱的前2 阶模态涡量在近壁面区分布明显，沿顺流向衰减.第1、2 阶模态的涡量分布的相位差约为π/2，该相位差和涡量分布值与尾流中Kar⁃man涡街的形成密切相关.第3、4阶模态涡量分布幅值较小，但沿顺流向的分布趋势明显，表征尾流中脱落的旋涡沿顺流向的能量输运过程［17］.从图3（b）和（c）中可看出，当施加均布式吹气控制后，均布多孔表面的圆柱尾流中POD 前2 阶模态涡量分布得到削弱，且向下游偏移，远离圆柱壁面；而第3、4 阶模态涡量分布得到增强.

试验工况的前4 阶POD 模态系数分布如图4 所示.从图4（a）可看出，无控圆柱的第1、2阶POD 模态系数幅值较大，且具有明显的周期性，结合图3（a）中模态涡量分布特征，进一步表明了前2 阶模态对尾流中的旋涡脱落起着主要的控制作用［17］.第3、4 阶POD 模态系数幅值较小，时间历程也不具有明显的周期性.当等效吹气系数CQ逐渐增大时，第1、2阶模态系数幅值减小，且周期性不再明显；第3、4 阶模态系数幅值增大，并达到与第1、2 阶模态系数幅值相似的水平，如图4（b）和（c）所示.

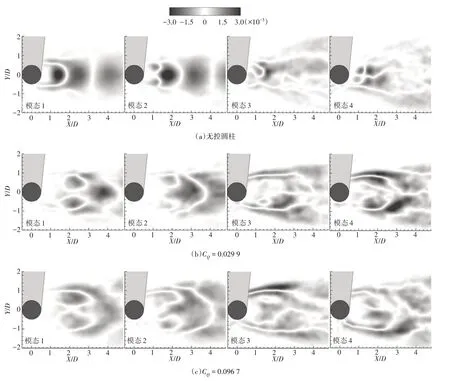
图3 前4阶POD模态涡量分布Fig.3 Modal vorticity distributions of the first four POD modes

POD 模态系数的均值和均方差（mean-squareerror，MSE）值如表2 所示，其中MSE值可描述模态系数的波动程度.从表2 中可看出，无控圆柱的第3 阶POD 模态均值的偏移较大，而第1、2 阶模态的波动程度最明显.当CQ=0.029 9 时，第1～4 阶POD 模态均值进一步发生偏移，而MSE值均得到了削弱，尤其是第1、2 阶POD 模态的削弱程度最大，即模态系数波动程度被明显抑制.当CQ=0.096 7 时，各模态的均值偏移幅度减小，而第3、4 阶模态的波动程度变大.以上结果与图4 中的现象一致，即随着等效吹气系数的增大，第1、2阶POD 模态得到了抑制，而第3、4阶模态被增强.

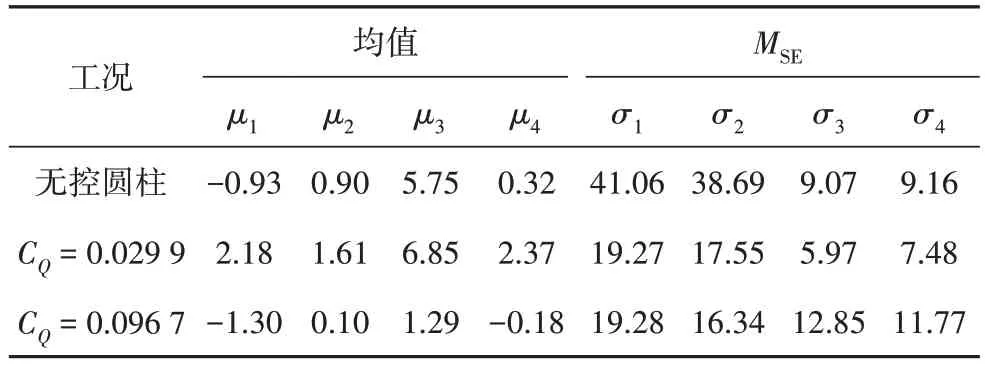
表2 POD模态系数均值与MSE值Tab.2 Mean and MSE values of POD modal coefficients

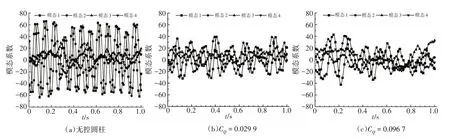
图4 前4阶POD模态系数分布Fig.4 Modal coefficient distributions of the first four POD modes

2.2 尾流瞬时特性

索结构尾流中一个旋涡脱落周期的瞬时面内涡量ωz分布如图5 所示，任意给定各工况的初始时刻t0，相邻时刻的时间间隔为T/4，其中T为各工况所对应的尾迹涡脱落周期，分别为0.08 s、0.11 s和0.12 s，对应的斯托罗哈数（St）为0.208、0.152 和0.139，其中无控圆柱的St值与Fey 等［16］在相同雷诺数下的研究结果相吻合.St为描述旋涡脱落周期或频率特征的常用的无量纲参数，其定义为：

式中：fv为旋涡脱落频率；T为旋涡脱落周期（fv=1/T）；D为钝体的特征长度即圆柱的外部直径；U∞为来流风速.从图5（a）中可以看出，无控圆柱两侧分离的剪切层之间相互作用明显，尾迹涡脱落模式为典型的“2S”模式，即一个周期内有两个反对称的旋涡脱落［18-19］，这种旋涡脱落模式在钝体尾流中所形成的一系列旋涡即所谓的Karman 涡街.随着等效吹气系数CQ的增大，剪切层间的相互作用减弱，涡量分布幅值减小，随时间的演变周期被改变，尾流中的旋涡脱落现象已不再明显甚至消失.

图5 一个周期内的瞬时涡量ωz分布Fig.5 Instantaneous vorticity ωz distributions within one cycle

2.3 DMD模态特性

图6 给出了无控圆柱的DMD 模态特征.图6（a）所示为DMD 模态特征值λj在复平面上的分布，实部为Re｛λj｝，虚部为Im｛λj｝，特征值λj也被称为Ritz值.从图6（a）中可以看出，DMD 模态的特征值为共轭复数对，主要分布在单位圆|λj|=1上，与Rowley 等［20］和张扬等［21］的研究结果相似.DMD 模态幅值分布随无量纲频率（St）的变化如图6（b）所示，根据幅值大小对模态进行降序排序后可以看出，第1 阶DMD 模态所对应的St值即为无控圆柱实际流场中的旋涡脱落频率所对应的St数，与2.2 节中的结果相吻合.图6中的结果表明，无控圆柱的DMD 模态主要分布于低频段，且主要模态的幅值分布较为集中.

图6 无控圆柱的DMD模态特征Fig.6 DMD modal characteristics of the uncontrolled circular cylinder

图7 所示为索结构在等效吹气系数CQ=0.029 9时的DMD 模态特征.特征值λj仍主要分布在复平面内的单位圆|λj|=1上，如图7（a）所示.与无控圆柱相比，该工况的模态幅值分布向低频段进一步偏移，主要DMD 模态的幅值得到增强，第2 阶模态所对应的St值与2.2节中的结果相同.

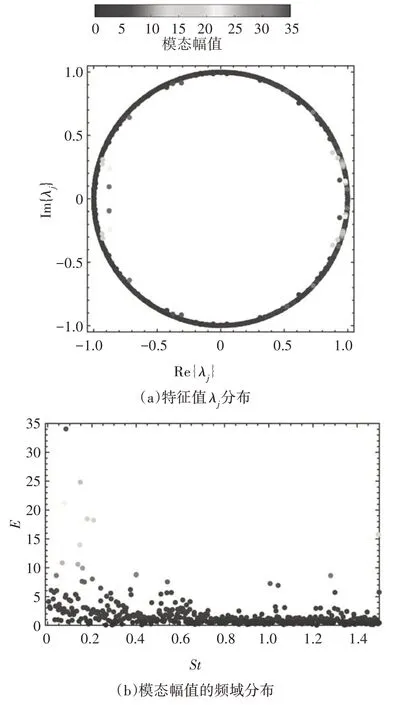
图7 CQ=0.029 9时的DMD模态特征Fig.7 DMD modal characteristics of the controlled case with CQ=0.029 9

等效吹气系数CQ=0.096 7 时的DMD 模态特征如图8 所示.与上述工况相比，有较多模态的特征值λj分布于复平面内的单位圆|λj|=1内部，表明流场已不再以中性稳定为主，如图8（a）所示.从图8（b）所示的模态幅值频域分布结果可以看出，DMD 各模态间的幅值分布趋于均匀，主要模态间的幅值差异已不再明显，表现出明显的宽频分布特征.

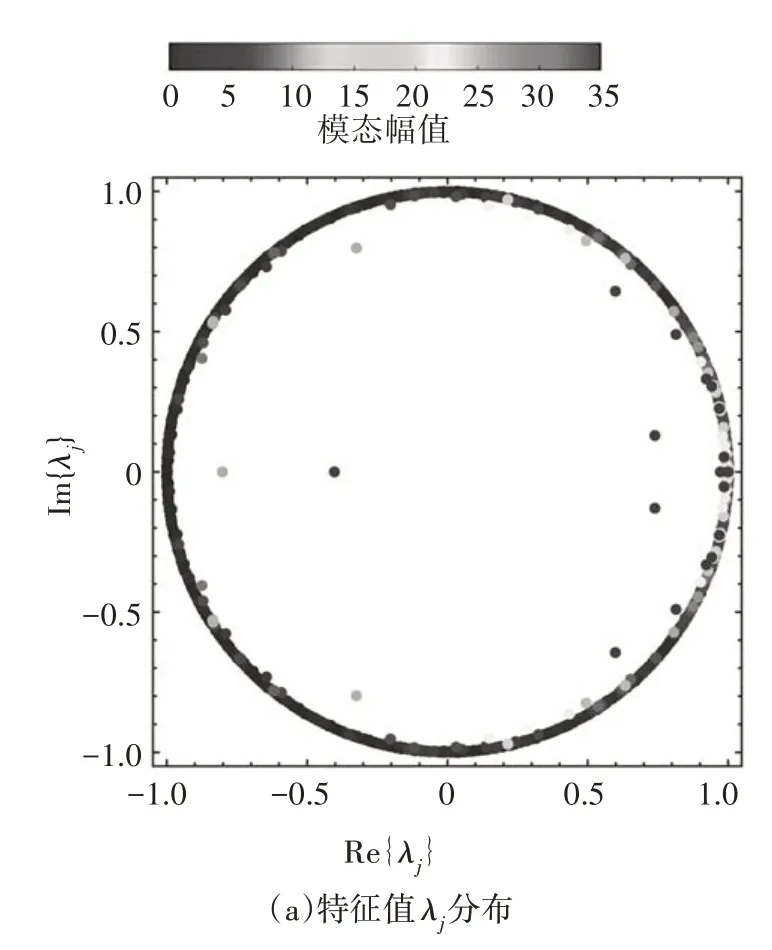
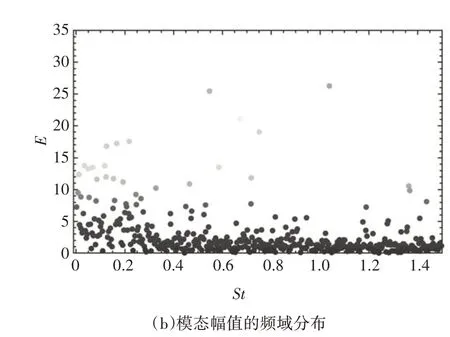
图8 CQ=0.096 7时的DMD模态特征Fig.8 DMD modal characteristics of the controlled case with CQ=0.096 7

2.4 时间平均特性

索结构尾流的时均流线和湍动能分布如图9 所示.从图9（a）中可以看出，无控圆柱的尾流回流区范围约为X/D≤1.7，-0.5 ≤Y/D≤0.5.尾流中的湍动能较大，峰值集中分布于X/D≈0.8 处.随着等效吹气系数CQ的增大，索结构尾流中的回流区尺寸变大，湍动能分布得到明显削弱，如图9（b）和（c）所示.当CQ=0.029 9 时，回流区范围约为X/D≤3.2，-0.8 ≤Y/D≤0.8；当CQ增至0.096 7 时，回流区范围扩大到X/D≤3.5，-1.0 ≤Y/D≤1.0.此现象也与图5 所示的索结构在吹气控制时的尾流区剪切层距离增大、相互作用受到削弱相一致.

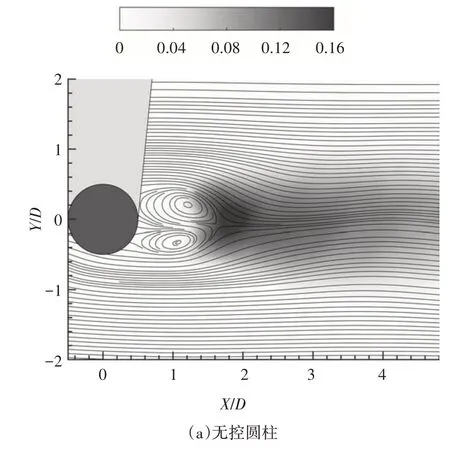
图9 时均流线和湍动能分布Fig.9 Distributions of time-averaged streamlines and turbulence kinetic energy

图10 所示为索结构尾流的时均雷诺切应力分布情况，在所有的工况中，雷诺切应力均关于Y/D=0呈反对称分布.从图10（a）中可以看出，无控圆柱尾流中的雷诺应力分布幅值较大，且距后驻点较近，表明湍流脉动对时均流动的影响较大.当进行吹气控制时，雷诺应力分布幅值受到削弱，且向下游偏移，如图10（b）和（c）所示.

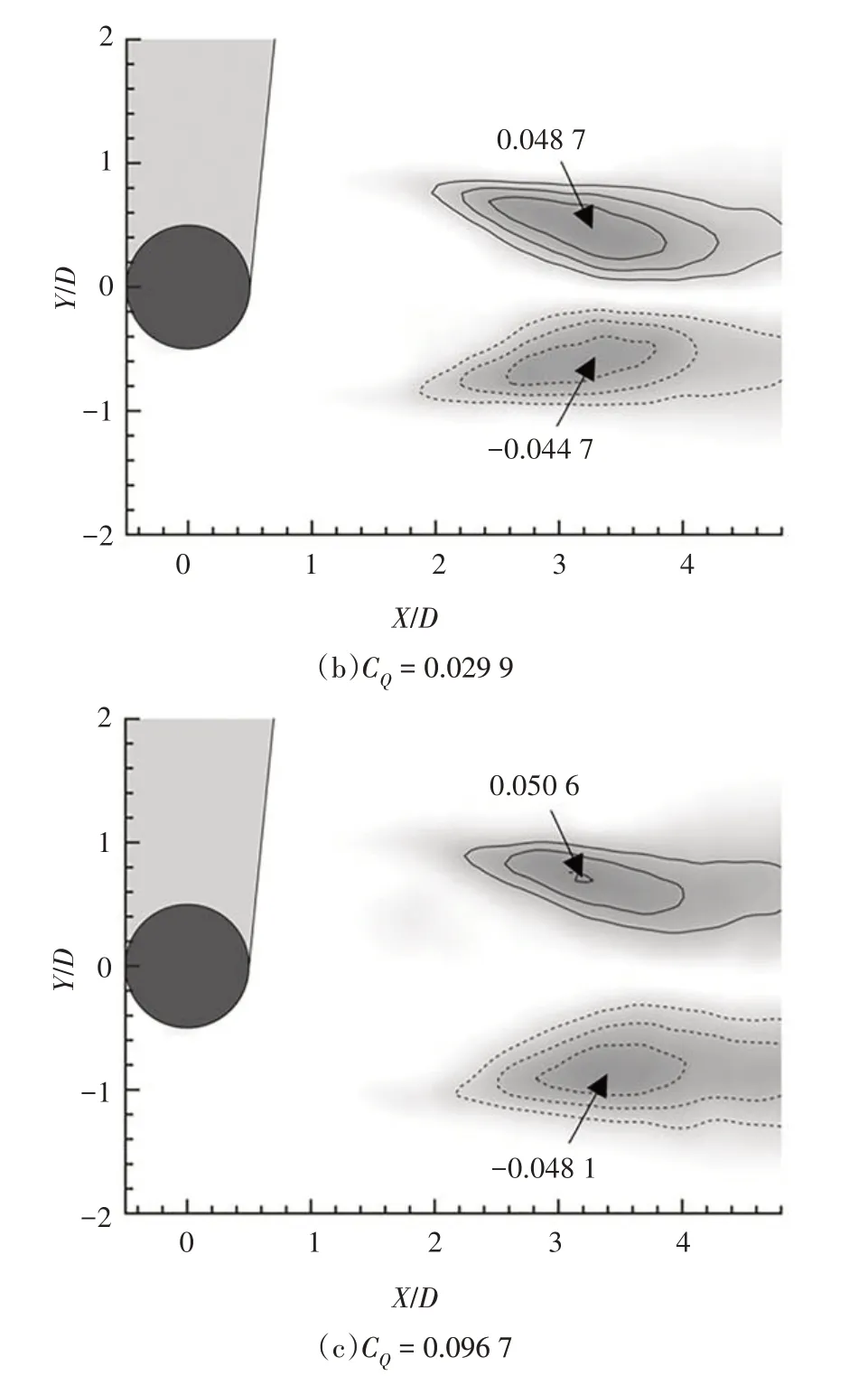
图10 时均雷诺切应力分布Fig.10 Distributions of time-averaged Reynolds shear stress

3 结论

本文进行了一系列风洞试验，通过PIV 系统测量了无控和均布式多孔表面吹气的索结构尾流速度场，在此基础上分析了各试验工况的瞬时和时均流动物理量变化情况，并通过POD 和DMD 等降阶模型，对主要的模态特性进行了分析和对比，得出如下主要结论：

1）与无控工况相比，控制工况的尾流场中各POD 模态阶次的能量分布趋于一致，流场中拟序结构的尺度趋于均一化；模态涡量分布得到削弱，第1、2 阶模态对反对称交替脱落的旋涡起到的控制作用得到抑制，而第3、4 阶模态表征的顺流向能量输运效应得到增强.

2）索结构尾流的旋涡脱落频率被改变，随着等效吹气系数CQ的增大，剪切层间的距离增大，其相互作用得到抑制.当CQ值足够大时，初始脱落的旋涡会消失.

3）当等效吹气系数CQ增大时，绕流场的DMD 模态特征发生了明显的变化，具体表现为：更多模态的特征值λj分布在复平面内的单位圆|λj|=1 中；具有高幅值的主要DMD 模态在频域中向低频偏移，随着CQ的增大，进一步地表现出宽频特征.

4）随着CQ的增加，索结构尾流中的回流区沿顺流向和横流向的尺度变大；湍动能和雷诺应力得到显著削弱；雷诺应力向下游偏移，湍流脉动对时均流动的影响得到抑制.