基于精确阻尼调控的桥梁竖弯涡振Sc 数影响
2022-06-06华旭刚马伟猛黄智文陈政清万田保孙英杰刘曙光
华旭刚,马伟猛,黄智文†,陈政清,万田保,孙英杰,刘曙光
(1.风工程与桥梁工程湖南省重点实验室(湖南大学),湖南长沙 410082;2.湖南大学土木工程学院,湖南长沙 410082;3.中铁大桥勘测设计院集团有限公司,湖北武汉 430056;4.中铁桥隧技术有限公司,江苏南京 210061)
主梁竖向涡振是大跨度桥梁在常遇风速下容易发生的一种风致振动现象.主梁涡振响应的锁定风速区间和幅值大小主要受主梁断面气动外形、来流特性和结构动力特性等因素的影响[1-3].在结构动力特性参数中,模态阻尼比和质量是两个重要参数,它们对主梁涡振响应的影响通常可归纳为无量纲参数Scruton数的影响[4].Scruton数简称Sc数,它是结构无量纲质量和阻尼比的乘积,最早由Scruton 在对烟囱等圆柱体结构涡振的研究中提出[5].对于主梁竖向涡振,文献[6]对Sc数的原始定义进行了修正,其表达式为Sc=4πmξ/(ρBD),其中m表示主梁单位长度的质量;ξ表示结构模态阻尼比;ρ表示空气密度;B和D分别表示主梁宽度和高度.本文将采用Sc数的上述定义形式.
研究Sc数对主梁涡振的影响是实桥涡振响应预测及控制的重要环节.一方面,大跨度桥梁各阶竖弯模态的等效质量和阻尼比都可能存在差异,因此要预测不同模态的涡振响应,就需要分析Sc数的影响规律.郭震山等[7]和王守强等[8]分别以虎门大桥和西堠门大桥为背景对大跨度悬索桥的模态阻尼比进行了统计分析,结果发现大跨度悬索桥的竖弯模态阻尼比一般随模态阶次的增大而减小.实际上,由于大跨度桥梁阻尼比实测统计资料较少,目前国内外不同桥梁规范对阻尼比的建议值也存在较大差异.例如,对于钢混组合缆索承重桥梁,我国抗风设计规范建议的模态阻尼比为1%[9],而英国桥梁设计规范BD 49/01 的建议值则为0.48%[10].另一方面,当采用调谐质量减振器等机械阻尼措施进行涡振控制时,可首先确定主梁涡振响应随模态阻尼比或Sc数的变化规律,然后再根据所需的附加模态阻尼比或Sc数开展阻尼器参数设计.
目前,有大量文献报道了气动外形和来流特性对桥梁涡振的影响规律[11-12],但有关Sc数对桥梁涡振的影响仍缺乏系统的研究.在试验研究方面,Klamo 等[13]研制了电磁电涡流阻尼装置,并依托该装置分析了阻尼对水中圆柱体结构横流向涡振振幅和频率的影响规律.Larsen[14]基于风洞试验研究了一个钝体箱形断面分别在均匀流场和紊流下的竖向涡振振幅随Sc数的变化规律,并提出了一种涡激力的广义范德玻振子经验模型.李永君等[15]以东海大桥颗珠山桥为背景研究了质量和阻尼比对桥梁扭转涡振的影响,发现增大质量参数或阻尼参数都可以减小扭转涡振幅值.Marra等[16]通过节段模型风洞试验研究了Sc数对宽高比为4∶1 的矩形断面竖向涡振的影响规律,并由此提出了改进的Scanlan 非线性经验涡激力模型,但只考虑了0°风攻角的试验工况.在理论研究方面,为了提高桥梁涡振响应的预测精度,近年来许多学者致力于拓展半经验涡激力数学模型的适用性,使之能够在不同的Sc数下成立[17-19].在针对海洋立管等圆柱体结构的流致涡振研究中,Van⁃diver[20]提出了一种新的无量纲阻尼参数,并分析了它在三维涡振幅值响应预测中的优势.Garcia 等[21]分析了圆柱体结构涡振中固有阻尼比对系统附加质量和升力的影响.
采用节段模型风洞试验和理论分析研究结构阻尼比或Sc数对桥梁涡振响应的影响,其关键在于为节段模型系统提供稳定、可靠和精确可调的线性黏滞阻尼.目前桥梁节段模型风洞试验中主要采用油阻尼桶、缠绕钢丝绳或电工胶带等方式来调节节段模型悬挂系统的阻尼比,但上述方法都有很明显的局限性.例如,油阻尼桶提供的剪切黏滞阻尼一般具有较好的线性特性,但其阻尼系数与剪切面的形状和面积相关,难以实现连续调节;缠绕钢丝绳或电工胶带产生的阻尼都在一定程度上依赖于材料之间的摩擦,因此都具有一定的非线性,也难以实现精确、连续调节[22].此外,若采用电磁电涡流阻尼,则可能存在电磁铁发热的问题.
为了开展Sc数对大跨度桥梁竖向涡振影响的精细化研究,本文首先研制了适用于桥梁节段模型风洞试验的、阻尼系数精确可调的永磁式板式电涡流阻尼器,结合电磁有限元分析和自由衰减振动试验验证了阻尼器的阻尼特性.然后通过改变节段模型系统的附加阻尼比来改变系统的Sc数,以带风嘴的开口断面钢混组合梁为研究对象,通过节段模型风洞试验研究了实桥在+3°、0°和-3°三个风攻角下的竖向涡振响应随Sc数的变化规律,并据此对桥梁高阶模态涡振响应进行了预测.
1 板式电涡流阻尼器研制及性能测试
1.1 永磁式板式电涡流阻尼器的基本构造
图1 给出了永磁式板式电涡流阻尼器的基本构造.可以看到,板式电涡流阻尼器由永磁体、永磁体背铁、导体板、底座和间距调节装置构成.其中,导体板固定在节段模型的端部,与节段模型一起沿竖向运动;底座固定在风洞地面,其距离地面的高度可以调节;永磁体分别布置在导体板的两侧,其中沿导体板运动方向的磁极交替布置,沿垂直于导体板运动方向的磁极相同布置.导体板两侧永磁体之间的空气间隙可连续调节,从而实现阻尼器的阻尼系数以及节段模型系统阻尼比的连续调节.永磁体背铁由高磁导率材料制作,这样使阻尼器自身形成闭合磁路,不会对试验仪器产生电磁干扰,同时还提高了电涡流阻尼器的耗能效率.永磁体采用钕铁硼稀土永磁体,厚度20 mm;导体板采用铝板,厚度6 mm.

图1 板式电涡流阻尼器原理示意图Fig.1 Schematic diagram of plate eddy current damper
本文只研究节段模型的竖向涡振,因此电涡流阻尼器安装在节段模型左右两端的中心位置,如图2所示.当节段模型振动时,模型带动导体板也做上下振动,从而使永磁体与导体板之间发生相对运动.于是导体板切割磁力线,并在其上产生电涡流,电涡流产生的磁场与永磁体磁场相互作用,产生一个阻碍导体板和永磁体相对运动的阻尼力,即电涡流阻尼力.从能量转化的角度看,电涡流阻尼器把节段模型的振动能量首先转化为导体板内的电能,并最终转化为热能耗散掉,由此产生了阻尼效应.

图2 板式电涡流阻尼器的安装照片Fig.2 The installation photograph of plate eddy current dampers
1.2 板式电涡流阻尼器性能
本文以钢混组合梁为研究对象,图3 给出了节段模型横断面设计尺寸,其中模型宽度B=0.633 m,高度D=0.046 m,长度L=1.740 m,每延米质量m=11.273 kg,竖向振动的固有频率fn=2.87 Hz,几何缩尺比λL=60,试验风速比λU=2.1.

图3 节段模型横断面图Fig.3 Standard cross section of section model
在开展节段模型风洞试验前,通过电磁有限元分析和节段模型的自由衰减振动试验对永磁式板式电涡流阻尼器的理想线性阻尼特性进行了验证.在电磁有限元分析软件COMSOL 中建立了板式电涡流阻尼器的有限元模型,分析了4 种不同气隙条件下板式电涡流阻尼器的阻尼系数随模型振动速度的变化规律,并根据节段模型系统的质量和自振频率把上述阻尼系数转换为节段模型系统的附加结构阻尼比.为了便于对比,不同振动速度下的附加结构阻尼比均除以速度为0.01 m/s时的附加阻尼比,以无量纲化.分析结果如图4 所示,可以看到,不管气隙如何变化,节段模型系统的附加结构阻尼比都几乎不随其振动速度(即导体铝板的振动速度)变化,说明文中板式电涡流阻尼器的阻尼性能与模型振动状态无关.需要说明的是,根据模型固有频率和以往试验中钢混组合梁断面的涡振响应大小,分析时保守估计了模型的最大振动速度为0.2 m/s,对应最大涡振振幅为0.011 m,约为0.24倍模型高度.

图4 附加阻尼比随振动速度的变化曲线Fig.4 Curve of additional damping ratio versus vibration velocity
板式电涡流阻尼器的线性阻尼特性还可以从安装阻尼器前后节段模型系统的附加阻尼比随振幅的变化上得到验证.图5 给出了无阻尼器时由自由衰减振动试验得到的节段模型阻尼比和频率随振幅变化曲线,可以看到,节段模型系统的阻尼比随节段模型振幅的增大而近似呈线性增大,但节段模型系统的固有频率随振幅变化非常小,可认为是常数.值得注意的是,无阻尼器时由自由衰减振动试验得到的阻尼包括因模型变形和构件摩擦等因素产生的机械阻尼,以及无风环境下的气动阻尼[23].
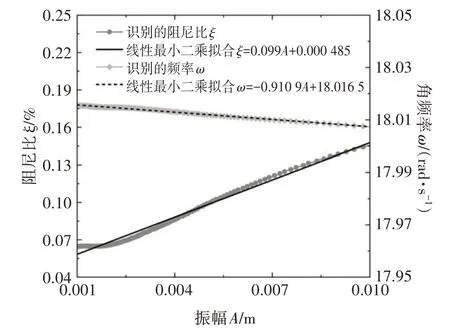
图5 无阻尼器时节段模型动力特性随振幅变化曲线Fig.5 Curve of dynamic characteristics versus amplitude of the sectional model without dampers
安装板式电涡流阻尼器后,首先通过自由衰减振动得到节段模型系统的总阻尼比随振幅的变化曲线,再减去无阻尼器时系统的阻尼比(见图5),就得到板式电涡流阻尼器提供的附加阻尼比.图6 根据附加阻尼比随振幅的变化结果进一步统计了附加阻尼比的平均值ξ0及其变动率δ随气隙大小的变化规律.其中ξ0为1~10 mm 的振幅区间内,附加阻尼比的平均值;变动率δ=(ξmax-ξmin)/ξ0,其中ξmax和ξmin分别为1~10 mm 振幅区间内,附加阻尼比的最大值和最小值.从图6 可知,不同气隙下附加阻尼比的变动率δ都很小,大部分工况都在4%以内.因此,不同气隙下附加阻尼比可认为是一常量,并可用平均值ξ0表示.

图6 附加阻尼比平均值及其变动率随气隙的变化Fig.6 Average value and variation rate of additional damping ratio under different air gaps
需要说明的是,本文在分析阻尼或Sc数对节段模型涡振响应的影响时,将计入阻尼器的附加阻尼、节段模型系统的机械阻尼和无风环境下的气动阻尼(即图5 中识别的系统阻尼),以下称为总阻尼.实际上,节段模型发生涡振时,应将无风环境下的气动阻尼排除在影响因素之外,但要准确分离机械阻尼和无风环境下的气动阻尼难度较大[24-25].考虑到无风环境下的气动阻尼相对附加阻尼较小,本文为了简化分析,把无风环境下的气动阻尼合并到机械阻尼中,得到的涡振预测结果将偏于保守.
为了展现板式电涡流阻尼器阻尼系数的连续可调功能,采用电磁有限元分析和节段模型系统的自由衰减振动试验,对比分析了节段模型系统的附加阻尼比随永磁体与导体板之间气隙大小的变化规律,结果如图7 所示.可以看到,随着气隙的减小,节段模型系统的附加阻尼比逐渐增大.当气隙大于4 cm 时,由阻尼器提供的附加阻尼比几乎为零;当气隙减小到2 cm 时,附加阻尼比可增大到2%,可完全抑制节段模型的竖向涡振.此外可以发现,由有限元分析预测的附加阻尼比与实测结果非常接近,证明了板式电涡流阻尼器设计方案的可行性.
2 阻尼及Sc数对节段模型涡振的影响
2.1 竖向涡振位移响应风速区间随阻尼的变化
因为机械阻尼和无风环境下的气动阻尼具有振幅依赖性,所以当附加阻尼较小时,系统的总阻尼及对应的Sc数也具有较明显的振幅依赖性.桥梁涡振研究的主要目的之一是预测实桥最大涡振振幅,因此可取各工况下节段模型最大涡振振幅对应的总阻尼比作为该工况下的名义阻尼比,再由此计算Sc数,即Sc=4πmξn/(ρBD),其中ξn表示节段模型名义阻尼比.
图8 为没有附加阻尼时,不同风攻角下节段模型的无量纲竖向涡振振幅随折减风速的变化曲线,其中无量纲振幅定义为η=y/D,无量纲折减风速定义为Vr=U/fnB,其中U为来流风速.可以看到,在+3º、0º和-3°来流风攻角下节段模型系统的名义阻尼比均为0.1%,主梁均只有一个竖向涡振锁定风速区间,且不同风攻角下的涡振锁定风速区间基本一致,无量纲最大涡振振幅约为0.12.

图8 无阻尼器时主梁竖向涡振振幅与风速关系Fig.8 Vertical vortex-induced vibration amplitude versus wind speed of main beam without dampers
通过板式电涡流阻尼器不断增大节段模型系统的附加阻尼比,得到不同风攻角下名义阻尼比不断增大时,节段模型的无量纲竖向涡振振幅随折减风速的变化情况,如图9 所示.可以看到,不同风攻角下,节段模型的竖向涡振最大振幅和涡振锁定折减风速区间均随着名义阻尼比的增大而逐渐减小,但变化趋势不同.例如,对于+3º风攻角,即使名义阻尼比增大到1%,主梁的竖向涡振也没有完全消失.而对于-3º风攻角,当系统的名义阻尼比略大于0.37%时,竖向涡振就基本消失.


图9 主梁竖向涡振随名义阻尼比变化曲线Fig.9 Curve of vertical vortex-induced vibration versus nominal damping ratio of main beam
2.2 最大竖向涡振振幅随Sc数的变化曲线
根据上一节试验结果进一步统计得到节段模型竖向涡振的最大涡振振幅随名义阻尼比及Sc数的变化曲线,分别如图10和图11所示.可以看到,随着名义阻尼比或Sc数的不断增加,不同风攻角下的最大涡振振幅不断降低,但不同风攻角下的变化规律不相同.+3º风攻角下的节段模型竖向涡振峰值响应下降最慢,-3º风攻角下的节段模型竖向涡振峰值响应下降最快,0º风攻角下的节段模型竖向涡振峰值响应下降速度介于前两者之间.此外,随着阻尼比或Sc数的增大,最大涡振振幅对阻尼比或Sc数的敏感程度逐渐降低.
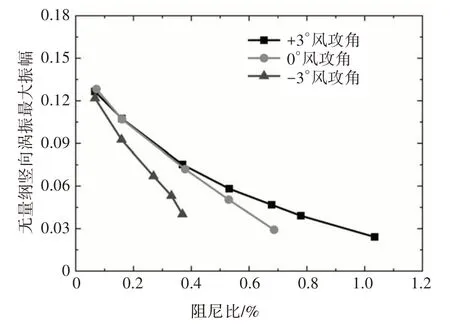
图10 主梁竖向最大涡振振幅与名义阻尼比关系Fig.10 Peak value of vertical vortex-induced vibration versus nominal damping ratio
2.3 最大竖向涡振振幅随Sc数的变化曲线拟合
利用板式电涡流阻尼器可实现节段模型系统阻尼比的连续调节,得到最大涡振振幅随阻尼比或Sc数的精确变化规律.但从实际工程的角度看,应尽量减少振幅预测所需Sc数的试验工况,提高试验效率.提高试验效率的一个重要方法就是对最大竖向涡振振幅随Sc数的变化曲线进行函数拟合.参考Sc数对圆柱体涡振振幅的影响规律[26-27],采用两种函数形式对图11 所示试验数据进行拟合,其中函数一为分数形式,函数二为幂指数形式,即

图11 主梁最大竖向涡振振幅与Sc数关系Fig.11 Peak value of vertical vortex-induced vibration versus Sc number

式中:a、b和c表示函数一的待拟合参数;a1和b1表示函数二的待拟合参数,从物理意义上看,a和a1表示当Sc数等于零时结构可能达到的极限涡振振幅;ηmax表示主梁无量纲涡振振幅.
不同风攻角下函数一和函数二的参数识别结果见表1,拟合函数和试验数据的对比如图12所示.从图12 可看到,在试验的Sc数范围内,函数一和函数二均能较好地拟合主梁的最大涡振振幅随Sc数的变化规律,但当Sc数小于试验范围时,函数一和函数二的拟合结果偏差逐渐增大.从表1 可看到,对于函数一,3 个风攻角下的极限涡振振幅基本相同,均在0.135 左右;对于函数二,从-3°风攻角到+3°风攻角,对应的极限涡振振幅逐渐减小.总体来看,函数二预测的极限涡振振幅大于函数一.

表1 最大涡振振幅随Sc数变化的拟合函数识别结果Tab.1 Fitting results of the dimensionless maximum vortex-induced vibration amplitude function

图12 主梁竖向涡振峰值与Sc数关系拟合Fig.12 Fitting of peak value of vertical vortex-induced vibration versus Sc number of main beam
选择合适的试验方案可在保证拟合精度的前提下进一步减少工作量,下面以+3°风攻角为例,说明试验方案对函数拟合精度的影响,结果如图13(a)~(d)所示.对于函数一:方案一的拟合误差最大,说明当Sc数小于试验范围时,函数一难以准确描述主梁涡振振幅随Sc数的变化规律.相反,若用Sc数较小时的试验数据预测高Sc数的主梁涡振响应,则相对误差较小(见图13(b)).试验方案三和试验方案四都保留了Sc数最小和最大的试验工况,然后再选取Sc数介于二者之间的一个或两个工况.从图13(c)和图13(d)可发现,上述两种方案的拟合误差都较小,可有效预测不同Sc数下的主梁涡振振幅.

图13 试验方案对Sc数拟合函数的影响Fig.13 Effect of test scheme on Sc number fitting function
对比函数一和函数二的拟合结果可发现,函数二能更精确地描述节段模型的最大涡振振幅随Sc数的变化规律,即使要预测的Sc数小于试验范围,函数二的预测结果也非常准确,因此函数二将用于下文实桥涡振响应预测研究.值得说明的是,函数二的适用性还有待针对不同的桥梁断面开展进一步研究.
3 实桥主梁高阶模态涡振响应预测
基于节段模型的最大涡振振幅预测公式(2),可进一步得到实桥各阶竖弯模态的涡振振幅预测公式:

式中:ηi,max表示某个风攻角下实桥第i阶竖弯模态的最大涡振振幅;λL表示几何缩尺比;λi,s表示第i阶竖弯模态的振型修正系数;λi,c表示第i阶竖弯模态的涡激力展向相关性修正系数.其他参数的物理意义如前文所示.
需要说明的是,主梁各阶竖弯模态的振型修正系数和涡激力展向相关性修正系数都与涡激力的数学模型和振型函数有关,目前尚缺乏定论.本文从工程实用的角度考虑,各阶竖弯模态的振型修正系数都按Scanlan 非线性涡激力模型和简谐波振型计算,即;涡激力展向相关性修正系数按完全相关考虑,λi,c=1.
通过结构有限元分析可得到大桥每延米的等效质量,各阶竖弯模态的阻尼比则参照英国抗风规范取为0.48%,由此计算得到大桥前15 阶模态的Sc数如图14 所示.可以看到,大桥各阶竖弯模态的Sc数基本相同,都在19左右.利用公式(3)可预测+3°风攻角和0°风攻角下,主梁各阶竖弯模态的最大涡振振幅,结果如图15 所示.图中还依据我国《公路桥梁抗风设计规范》(JTG/T 3360-01—2018)[9]给出了各阶竖弯模态的涡振振幅容许值.可以看到,各阶竖弯模态的最大涡振振幅基本相等,但对应的规范容许值则随着竖弯频率的增加按反比例关系逐渐减小.因此,高阶模态的涡振振幅比低阶模态更容易超过规范容许值,而且模态阶次越高,可能超过规范容许值的程度也越大.综上,对于大跨度悬索桥必须检验高阶竖弯模态的涡振振幅是否满足规范要求.仅对一阶竖弯模态进行最大涡振振幅检验,一般是偏于不安全的.

图14 各阶竖弯模态的Sc 数Fig.14 The Sc number of each vertical bending mode
4 结论
1)永磁式板式电涡流阻尼器可为节段模型系统提供连续可调的、精确的线性黏滞阻尼,为节段模型涡振试验的阻尼比调节提供了新方法.
2)不同风攻角下的主梁竖向涡振峰值都随Sc数的增大而减小,但风攻角不同,变化的规律也存在显著差异.总体来看,幂指数函数能较好地反映主梁竖向涡振峰值随Sc数的变化规律.
3)大跨度悬索桥各阶竖弯模态的涡振振幅基本相等,高阶模态的涡振响应更容易超过规范限值,应予以重视.
