混合桥面横向连接构造静力性能

2022-06-06戴昌源邵长宇苏庆田

同济大学学报（自然科学版） 2022年5期

戴昌源，邵长宇，苏庆田，陈亮

（1. 上海市政工程设计研究总院（集团）有限公司，上海 200092；2. 同济大学土木工程学院，上海 200092；3. 上海高性能组合结构桥梁工程技术研究中心，上海 200092）

大跨径斜拉桥结构通常对自重较为敏感，多采用强度高自重小的钢材作为加劲梁的主要材料。正交异性钢桥面（OSD）以其明确的受力方式、较高的承载力和较小的自重在大跨度钢结构桥梁中大规模应用，但其疲劳［1-4］和铺装［5-7］问题一直是桥梁运营过程中难以避免的顽疾，其中重载交通是造成上述问题的一个主要原因。通过对大跨度桥梁交通流的分析发现，重载车辆主要行驶在外侧慢车道［8］。

相关研究表明，超高性能混凝土（UHPC）华夫板具有较好的疲劳性能。Aaleti 等［9］采用放大的荷载幅对UHPC 华夫板进行了100 万次疲劳循环加载，100 万次循环加载后UHPC 华夫板竖向刚度的降幅在8%以内，肋底部最大裂缝宽为0.05 mm，并且在整个疲劳加载过程中最大裂缝宽度保持不变，表明UHPC 华夫板具有较好的疲劳性能。邵旭东等［10］基于有限元和UHPC 材料S-N 曲线预测得到UHPC 华夫板疲劳寿命超过1 000 万次。此外，Aaleti 等［9］、Toutlemonde 等［11］、Honarvar 等［12］、Baby等［13］、邱明红等［14］对UHPC华夫板的受弯承载力、正常使用极限状态性能、双向受弯和冲剪性能、结构构造优化等的研究结果表明，该结构强度高、自重相对较小，适合作为桥面结构。因此，提出将斜拉桥流线型扁平钢箱梁桥面结构最外侧慢车道及车道以外的部分更换为UHPC 华夫板，中间车道和快车道仍采用正交异性钢板，组成混合桥面体系。

混合桥面系统在桥面横向由2 种桥面形式组成，连接2 种桥面的横向连接构造协同两侧桥面共同承担荷载并起到荷载传递与分配的作用。实际工程结构中少有不同类型桥面横向连接的实例，但不同类型桥面纵向连接在混合梁斜拉桥［15］、混合梁自锚式悬索桥［16］、混合梁连续梁桥和连续刚构桥［17］中较为多见。针对混合梁结合部的构造形式、刚度平顺性［18］、传力机理［19］、静力性能［20］以及在结构中的合理位置［21］等已有较多相关研究，并成功应用在多多罗大桥、鄂东长江大桥、诺曼底大桥［22］等特大型桥梁中，验证了构造的可靠性。混合桥面横向连接构造的作用为连接横向两侧不同种类的桥面板，使混合桥面能够共同承受上部车辆荷载并将荷载传递到横梁、横隔板等构件，与混合梁桥钢混结合部构造的作用有所不同。浙江台州椒江二桥（组合梁斜拉桥）采用了类似的混合桥面横向连接构造［23］，但机动车行车道部分为混凝土桥面板，非机动车道部分为正交异性钢桥面板。由于非机动车道荷载相对较小，并且连接位置恰好在箱室外侧腹板位置，因此两侧桥面可直接将荷载传递到箱梁腹板，横向连接构造并不协同两侧桥面共同受力。

鉴于现有结构中类似构造较少，因此在考虑传力均匀平顺的原则上确定了一种混合桥面横向连接构造，并针对此连接构造的静力性能进行试验和理论研究。

1 桥面横向连接构造

UHPC 华夫板-正交异性钢板混合桥面系统如图1所示。箱梁外侧UHPC华夫板与钢箱梁腹板翼缘通过剪力钉连接，与常规组合梁相同，在箱梁内侧则需横向连接2种不同形式的桥面。正交异性钢板刚度相对较低，易发生局部变形，而UHPC华夫板刚度相对较大，因此两者的连接构造如何使两侧刚度平顺过渡尤为重要。

图1 UHPC华夫板桥面-正交异性钢板桥面混合桥面系统Fig.1 UHPC waffle deck-OSD hybrid deck system

横向连接构造如图2 所示。L 型钢板与正交异性钢板部分焊接，内侧设置剪力连接件，通过后浇湿接缝与预制UHPC华夫板连接。L型钢板下焊接一个T型加劲肋。在实际工程中亦可采用纵隔板代替T 型加劲肋。正交异性钢板中U 肋间净距一般为300 mm，为了使连接构造刚度过渡平顺，可降低最靠近连接构造的U 肋与L 型钢板的距离（见图2 中m），提高局部刚度。连接构造细节与扁平钢箱梁中纵隔板顶板焊缝类似，并未引入新的疲劳细节。同时，此构造在2个车道中间位置，并非车轮高频作用位置。文献［24］中对运营近20 年后的南京长江三桥正交异性钢桥面疲劳裂缝进行统计，共发现998处疲劳裂缝，其中有57%分布在重车道范围内。在重车道和中间车道之间的纵隔板顶板焊缝中仅发现5 条疲劳裂缝，由此可见，若能妥善处理此处构造细节、保证焊接质量，则可确保构造的疲劳寿命。

图2 横向连接构造示意图Fig.2 Configuration of transverse connection detail

2 试件设计

正、负弯矩作用试件的断面包括一个U肋宽度的正交异性钢板、横向连接构造和一个U肋宽度的华夫板，总宽度为1 584 mm，如图3所示。对于正交异性钢板，顶板厚16 mm，U肋厚8 mm；对于横向连接构造，T型加劲肋翼缘厚20 mm，宽度180 mm，其余部分板厚12 mm。正弯矩作用试件跨度为4 m，横隔板外侧悬挑0.15 m。负弯矩作用试件中间设置一道横隔板，横隔板距离两侧支点1.635 m，支点外侧伸出0.15 m。试件平面和立面构造如图4所示。

图3 正负弯矩作用试件断面（单位：mm）Fig.3 Cross section of positive and negative bending specimens(unit:mm)

图4 正、负弯矩作用试件平面和立面图（单位：mm）Fig.4 Plane and elevation of positive and negative bending specimens(unit:mm)

3 加载方案与测点布置

正弯矩作用试件加载方式采用跨中单点加载，负弯矩作用试件加载方式为将试件倒立，从上向下加载。选用2 个1 500 kN 的作用器并联，合计加载力为3 000 kN，作用器荷载通过分配梁传递到试件，如图5所示。

图5 加载方式Fig.5 Loading setup

测点布置方面，正弯矩作用试件在跨中断面和一侧四分点断面布置应变片，出于节省篇幅考虑，这里仅给出后续应变结果中用到的跨中断面应变片，如图6所示。图6中，M表示跨中断面，S表示钢结构上的应变片，C表示混凝土上的应变片，R表示钢筋上的应变片。

图6 正弯矩作用试件跨中位置应变片布置（单位：mm）Fig.6 Layout of strain gauges at midspan of positive bending specimen (unit:mm)

负弯矩作用试件在4 个断面上布置了应变片，分别为中间横隔板断面（M 断面）、两侧截面突变断面（L 断面和R 断面）、M 断面与一侧支座之间的中间位置（R1 断面）。应变片编号中字符含义与正弯矩作用试件相同，同样仅给出后续应变结果中引用到的L断面应变片，如图7所示。

图7 负弯矩作用试件应变片布置（单位：mm）Fig.7 Layout of strain gauges for negative bending specimen (unit:mm)

4 材性试验

测试了钢板和钢筋的屈服强度（fy）与极限强度（fu），测试结果如表1所示。

表1 材性试验结果Tab.1 Material test results

对于UHPC，测试100 mm×100 mm×100 mm立方体试块抗压强度和棱柱体试块弹性模量，除此之外还进行了三点加载缺口梁试验。制作3个尺寸为550 mm×150 mm×150 mm 的棱柱体试件（S1、S2和S3）。在试件中部与浇筑时上表面相邻的光滑表面上用可以控制深度的钻石锯切割一个25 mm深度、5 mm 以内宽度的缺口，如图8 所示。三点弯曲加载时，采用蝶式引伸仪测量缺口张开的位移，得到荷载-裂缝张开位移（CMOD）曲线，通过式（1）转化为残余应力-CMOD曲线，如图9所示。

图8 缺口梁三点加载试验（单位：mm）Fig.8 Three-point bending test on notched beam(unit:mm)

式中：fR为残余应力；F为外荷载；l为试件跨度；b、hsp分别为试件截面宽度和去除缺口后截面高度。图9中，fR，1和fR，3分别为裂缝张开位移为0.5 mm 和2.5 mm时对应的残余应力。

图9 缺口梁三点加载试验结果Fig.9 Three-point bending test results on notched beam

5 试验结果

5.1 正弯矩作用试件

荷载达到300 kN时，正弯矩作用试件跨中位置纵肋底部可以观察到裂缝，但裂缝宽度小于裂缝观测仪可以测量的最小值0.02 mm。荷载达到800 kN时，纵肋侧边四分点断面附近出现较多斜裂缝。荷载继续增加到1 100 kN 时，跨中位置主裂缝扩展到上翼缘，并且裂缝逐渐横向贯穿，裂缝中可以观察到明显的纤维桥接作用。当荷载增加到2 221 kN 时UHPC压碎，试件竖向变形达到160 mm，停止加载，破坏模式如图10所示。

图10 正弯矩作用试件破坏模式Fig.10 Failure mode of positive bending specimen

加载过程的荷载-位移曲线如图11所示。从图11 可以看出，荷载在1 500 kN 左右后出现明显的非线性行为。UHPC华夫板侧变形显著大于正交异性钢板侧，表明试件在加载过程中出现了一定程度的横向倾斜，这可能是由加载过程中UHPC 华夫板开裂、刚度逐渐降低而导致的。

图11 正弯矩作用试件荷载-位移曲线Fig.11 Load-displacement curve of positive bending specimen

弹性阶段应变分布如图12所示，构件上翼缘顶面UHPC华夫板部分平均应变比正交异性钢板部分大74.1%。UHPC华夫板部分表现出明显的剪力滞效应，纵肋位置应变较大，而边缘和中间位置应变较小。正交异性钢板部分在外侧U肋腹板与钢顶板连接位置（MS1）应力显著大于其他位置（MS2～MS4）。正交异性钢板部分和UHPC华夫板部分弹性阶段断面应变分布符合平截面假定，两者中性轴位置与顶面的距离分别为60.2 mm和51.8 mm。进入非线性阶段后正交异性钢板部分的应变显著大于UHPC华夫板部分（见图13），造成这种现象的原因可能为UHPC华夫板逐渐开裂和压碎，其刚度退化，荷载转移到正交异性钢板部分。

图12 正弯矩作用试件弹性阶段应变分布Fig.12 Strain distribution for positive bending specimen in elastic stage

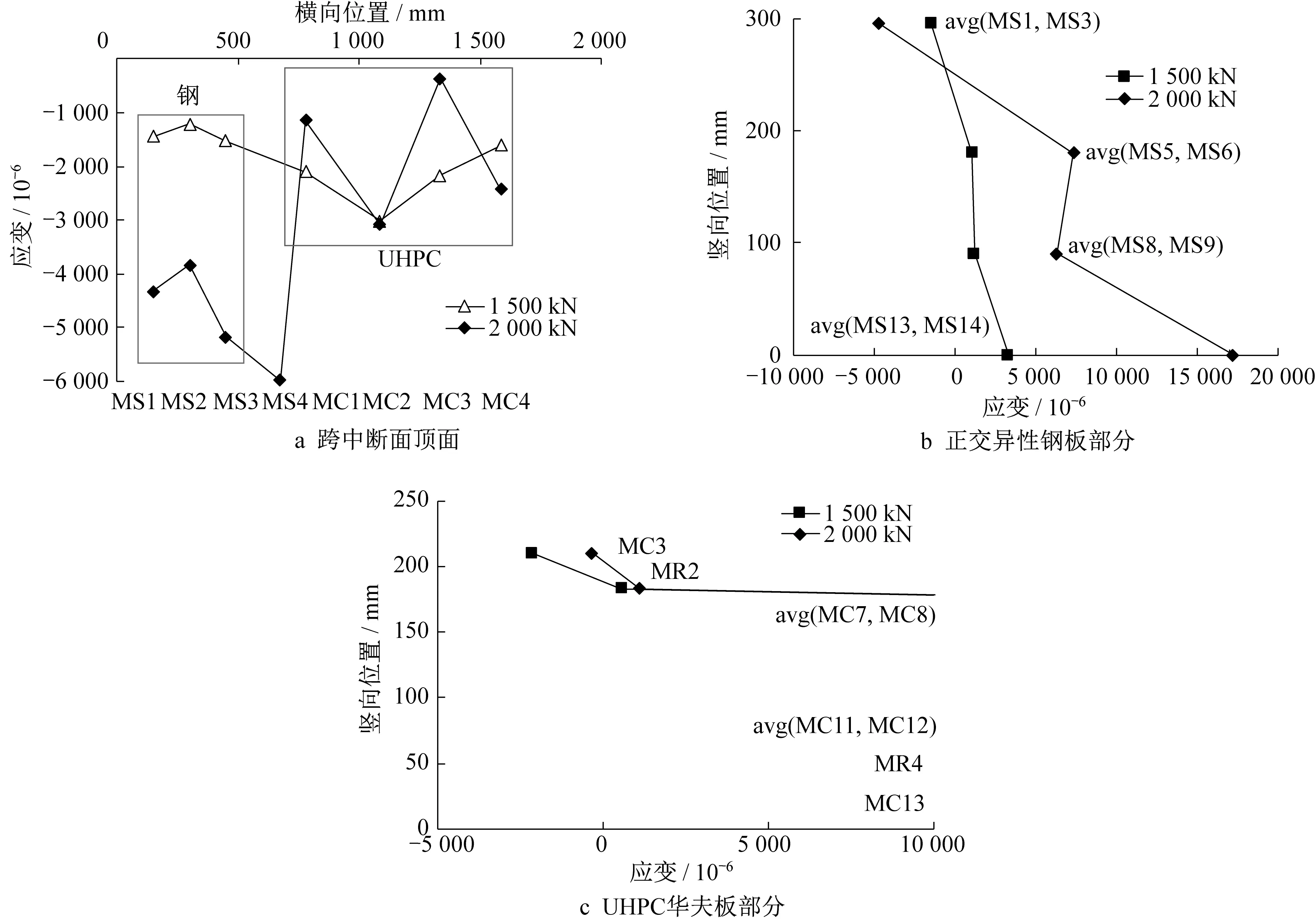
图13 正弯矩作用试件塑性阶段应变分布Fig.13 Strain distribution for positive bending specimen in plastic stage

加载过程中主裂缝宽度-荷载曲线如图14所示。当荷载超过1 700 kN时，裂缝宽度超过4 mm，并且试件周围区域已经不安全，因此停止裂缝宽度的测量。裂缝宽度随荷载的增加而增大，而且增加的速率增大，荷载为779 kN（跨中弯矩779 kN·m）时，裂缝宽度达到0.2 mm，该值为《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362―2018）对钢筋混凝土构件在Ⅰ类和Ⅱ类环境中的裂缝宽度限值。《公路桥涵通用规范》中规定车辆荷载后轮轴重为140 kN，将车辆荷载两重轴在试件的跨度范围内进行最不利正弯矩布载，在跨中产生的弯矩为182 kN·m，则试件具有的超载能力为779/182=4.28倍。

5.2 负弯矩作用试件

负弯矩作用试件的破坏模式如图15 所示。加载到400 kN时，在靠近R断面位置观察到了一条肉眼可见的裂缝。荷载为500 kN时，肉眼观察到的裂缝增多，间距和宽度均较小，并且分布在R断面和L断面两侧，但两者之间裂缝较少。出于安全考虑，裂缝宽度的测量在1 600 kN 时停止，此时最大裂缝宽度已经超过0.5 mm。此后，随着荷载增加，R 断面和L 断面位置的裂缝发展为主裂缝。当荷载达到2 093 kN时，中间隔板位置U肋和T型加劲肋屈曲，屈曲部位如图15c、e所示。此后，试件位移显著增加但荷载保持不变，当位移增加到100 mm 时停止加载。

图15 负弯矩作用试件破坏模式Fig.15 Failure mode of negative bending specimen

荷载-位移曲线如图16 所示。荷载超过1 300 kN 后，荷载-位移曲线表现出显著的非线性特征。与正弯矩作用试件相同，加载过程中试件出现一定程度的横向倾斜。局部屈曲发生后，荷载不再增加而变形持续增长。

图16 负弯矩作用试件荷载-位移曲线Fig.16 Load-displacement curve of negative bending specimen

弹性阶段L 断面上表面应变分布如图17 所示。UHPC 华夫板部分的应变大于正交异性钢板部分，此阶段正交异性钢板部分和UHPC华夫板部分应变分布较好地符合平截面假定。进入非线性阶段后断面L 应变分布如图18 所示，中间横向连接构造位置应变大幅增加，向两侧应变逐渐递减。

图17 负弯矩作用试件弹性阶段应变分布Fig.17 Strain distribution for negative bending specimen in elastic stage

图18 负弯矩作用试件塑性阶段应变分布Fig.18 Strain distribution for negative bending specimen in plastic stage

破坏时UHPC 华夫板上表面的裂缝分布如图19a 所示。裂缝间距小、数量多，长度普遍较短。R断面和L断面之间没有裂缝出现。随着加载的进行裂缝12 号和2 号逐渐发展成为主裂缝，裂缝宽度显著增加。

选取并测量了如图19a 所示裂缝2 号、4 号和12号在各级荷载下的宽度，如图19b 所示。在裂缝宽度的最后观测阶段（外荷载为600 kN）2号裂缝的宽度最大，为0.6 mm。4 号裂缝宽度首先达到0.2 mm，对应荷载为1 066 kN。同样将车辆荷载两重轴在试件的横隔板位置进行最不利负弯矩布载，在横隔板位置产生的负弯矩为98 kN·m，则试件具有的超载能力为1 066/98=10.88倍。

图19 负弯矩作用试件裂缝宽度-荷载曲线Fig.19 Crack width-load curve of negative bending specimen

6 截面弹塑性承载力分析

6.1 基本理论

本试验试件中采用了UHPC，其受拉开裂时混凝土并未完全退出工作，由于钢纤维的作用，裂缝之间仍然存在残余应力，这在开裂后对断面的承载力有不可忽略的贡献。考虑UHPC 材料受压、受拉时不同本构模型，采用弹塑性断面分析方法［25］计算试件的抗弯承载力与弯矩-曲率曲线。

主要分析流程如下：

（1）将断面离散成矩形块。

（2）假定一个中性轴位置x和截面顶端应变εtop，截面高度为H，中性轴与截面底端间距离为x，此时断面曲率

Zhang等[6]对Sagae进行了改进，使用线性模型对决策序列进行预测，从全局的角度对决策进行了考量，采用泛化的感知器算法对模型的参数进行训练，模型解码时，不再像Sagae使用确定性方式，而是引入BeamSearch策略，实验中讨论了Beam-size和训练数据集的大小对实验结果的影响，可惜的是此文只给出了在CTB上的实验结果。

对于每一个矩形块，假设其上缘和下缘与截面底端距离分别为y1和y2，则对于矩形块内部任意位置y（y1＞y＞y2），应变

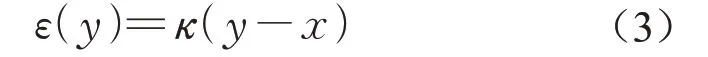
（3）通过数值积分和材料应力-应变关系计算每个矩形块的合力大小和作用点。

（4）计算所有矩形块的合力，这是一个关于x的函数，令合力为零，通过二分法求解x。

（5）将所有矩形块的合力乘以其作用点到中性轴的距离并求和，即可得到当前断面的抗弯承载弯矩M。

（6）给出一组连续的断面顶端应变εtop，可以计算出每一个εtop对应的断面曲率和断面弯矩，由此即可绘制出弯矩-曲率曲线。

6.2 材料模型

钢材的本构关系采用文献［26］中建议的考虑屈服后强化阶段的三线性模型，给定钢材的屈服强度fy、极限强度fu和弹性模量Es，可依据式（4）～（8）计算钢筋的本构关系曲线，如图20所示。

图20 钢材本构关系Fig.20 Stress-strain curve of steel

对于UHPC，受压时参照日本［27］、瑞士［28］和法国［29］等UHPC结构设计规范的建议，采用了双线性应力-应变曲线，如图21a所示，其中fc为UHPC抗压强度，εc0为应力达到抗压强度时的应变，εcu为抗压极限应变。受拉时采用了Fib model code 2010 中纤维混凝土受拉本构关系CASE（Ⅱ），如图21b所示。受拉本构曲线中的关键参数通过前文三点加载缺口梁试验获得。图21b中，fct为UHPC的抗拉强度，εt为相应应变，εSLS为裂缝张开位移0.5 mm 时的等效应变，fFts=0.45fR，1为此时的残余应力，εULS为裂缝张开位移2.5 mm时的等效应变，fFtu=fR，3/3为此时残余应力，εu为裂缝张开位移等于纤维长度一半时的等效应变。

图21 UHPC本构关系Fig.21 Stress-strain curve of UHPC

6.3 结果分析

正弯矩作用试件全断面承载力与全断面弯曲曲率的关系如图22a所示。整个断面的发展过程分为3个阶段。第一阶段断面处于弹性阶段，初始屈服时的截面弯矩为1 300 kN·m，此阶段实测弯矩-曲率曲线与计算得到曲线吻合度较高，说明理论分析得到的断面刚度与实测断面刚度能够较好吻合。断面弯矩超过1 300 kN·m后，弯矩-曲率曲线表现出明显的非线性特征，进入第二阶段。断面弯矩超过1 700 kN·m后，实测弯矩-曲率曲线高于计算曲线。最后，弯矩-曲率曲线趋于水平，进入第三阶段。理论分析得到的断面抗弯承载力极限值为2 063 kN·m，与实测值2 221 kN·m相差7.11%，表明弹塑性断面分析可以准确预测断面的刚度与抗弯承载力。

图22b为负弯矩作用试件加载过程中的弯矩-曲率曲线。曲线同样表现出明显的三阶段特征，弹性阶段实测弯矩-曲率曲线低于计算曲线，造成此结果的原因是在曲率计算位置处存在横隔板和截面突变，使得应变分布较为复杂，有限的应变片布置难以准确地反映真实应变分布，进而影响曲率计算，而弯矩-曲率计算曲线是以理想的L断面（或R断面）形状进行的，因此造成计算结果与实测结果有较大误差。计算曲线与实测曲线均在800 kN·m时进入第二阶段。在第二阶段，断面弯矩为1 538 kN·m时试件发生局部屈曲，达到极限承载力，未能进入第三阶段。若理论计算中不考虑局部屈曲的影响，进入第三阶段后断面的塑性极限抗弯承载力为1 926 kN·m，这说明按照强度理论计算负弯矩作用的混合桥面承载力时必须考虑钢板局部屈曲产生的强度折减效应。