控制疫情传播的多模式交通收费与补贴政策

郑 煜

（上海理工大学管理学院，上海 200093）

传染性疾病对全世界公共卫生是巨大的威胁，了解病毒的传播途径对于传染病的防控非常重要。虽然与病毒传播控制相关的问题已被广泛研究，但是大部分集中在公共卫生与行政政策制定等领域。经验表明，大部分流行病最初是通过交通系统进行跨区域传播，但从交通运输渠道控制病毒传播的研究却相对被忽视。因此，提出一种突发公共卫生事件下的交通应急管理方法（下文简称公共卫生交通管理方法），从方法论角度给出解决方案。以新冠肺炎传播为研究对象，基于该方法提出控制疫情大规模传播的最优交通管理方案。

1 文献综述

1.1 交通分配模型与双层规划模型

交通分配模型可以较好地再现实际交通状态，对交通网络的使用情况作出分析与预测。正确的交通分配模型可为交通管理与控制、动态路径诱导等提供依据。针对不同的交通网络结构以及用户出行选择行为，Sheffi［1］、黄海军［2］、唐铁桥等［3］提出了不同的交通分配模型。从交通出行方式多样性角度，可将交通分配模型分为单模式交通分配模型和多模式交通分配模型；根据用户的出行选择行为（如路径选择、出行方式选择、目的地选择等）是否随机，交通分配模型又可分为（确定）用户均衡模型和随机用户均衡模型。本研究中考虑交通出行方式的多样性以及用户路径选择行为的随机性，构建多模式随机交通分配模型。采用双层规划模型表示交通管理问题。对于上层模型，交通管理者通过设计交通管理方案使得整个交通网络的性能达到最优（如系统总出行时间最小、社会福利最大等），而下层模型是描述出行者在交通网络中的交通出行行为。Yang等［4］总结了近30年来经典的城市道路拥挤收费模型，其中大部分利用双层规划刻画管理决策与交通流分布之间的关系。

1.2 突发疫情下交通应急管理研究

在对交通运输网络疫情传播进行有效建模的基础上分析交通运输活动影响疫情传播的机理，继而对交通网络运行状态进行调控是突发疫情下交通应急管理的核心问题之一。经调查后发现，已有研究主要通过相变分析、网络分析、数值仿真等方法，定位关键调控交通因子、参数，寻求最佳防控措施。

文献［5-7］中采用病毒扩散模型研究感染人数随时间演化的规律，常见的病毒扩散模型有SIR、SIS、SEIR等（S、I、R、E为流行病学分类通常使用的缩写词，S 类代表易受感染的个体，I 类代表有传染性的个体，R 类代表感染后获得永久免疫力的康复个体，E 类代表接触过感染者但不存在传染性的个体，在一个模型中选择包含哪些类别取决于被建模的特定疾病的特征和建模的目的）。通过系统相变分析计算病毒扩散模型的临界值，得到系统发生跳变或达到稳态2种状况下感染人数关于疾病传染参数的表达式，并通过控制参数值寻求最佳防控措施。相变分析方法适用于模型结构简单并且各级相变状态存在解析解的情况。Bota等［8］分析了某个地区乘客的公共交通出行方式，定义了一种公共交通系统乘客出行接触网络，然后基于网络分析提出了能有效识别需要监控的网络关键组成部分的方法，最后通过模型计算验证该方法的可靠性。网络分析方法适用于网络规模不大、交通线路较单一且交通需求方式较为固定的传染病传播模型。近年来，研究者们综合利用数学模型和统计模型，基于多源信息对传染病扩散规律进行建模，并通过数值模拟对病毒传播的时空过程进行描述［9-11］。数值模拟方法的分析过程简单且分析结果直观，但对数据的充分性与可靠性依赖度较高。针对我国在此次新冠肺炎疫情防控中出现的问题，谢驰等［12］指出了交通运输管理的重要性，从管理科学角度分析疫情期间高感染风险的出行需求，并设计合理的交通管理方案，从而安全有效地调度有限的交通资源。

2 突发公共卫生事件下交通应急管理

不同于其他突发事件的交通应急管理模式，突发公共卫生事件下交通应急管理的基本原则有［13］：突发公共卫生事件下交通应急预案的制定，应当以突发事件的传播特性为依据，对与突发事件传播有关的交通运输方式以及交通区域加强防治抵御工作；在确保传染病病毒传播和蔓延抑制的前提下，尽量做到交通不中断、客流不中断；重大传染病疫情发生后，应当对可能传播传染病的交通工具、乘运人员、货物以及应急工作人员采取消毒和其他卫生防护措施。依据以上原则，将交通大数据与交通流分配、交通优化理论相结合，提出公共卫生交通管理方法。支持公共卫生交通管理方法可行的前提条件包括：第一，公共卫生事件的传播具有规律性，通过历史事件得来的交通管理经验可为以后相似公共卫生事件的交通应急处理提供指导依据；第二，除交通因素外的其他应急管理措施（如政府规定的强制隔离措施、以社区为单位的进出管控等）的执行力度与施行效果保持不变，只考虑交通因素对突发公共卫生事件传播的影响。公共卫生交通管理方法包含2个阶段，如图1所示。

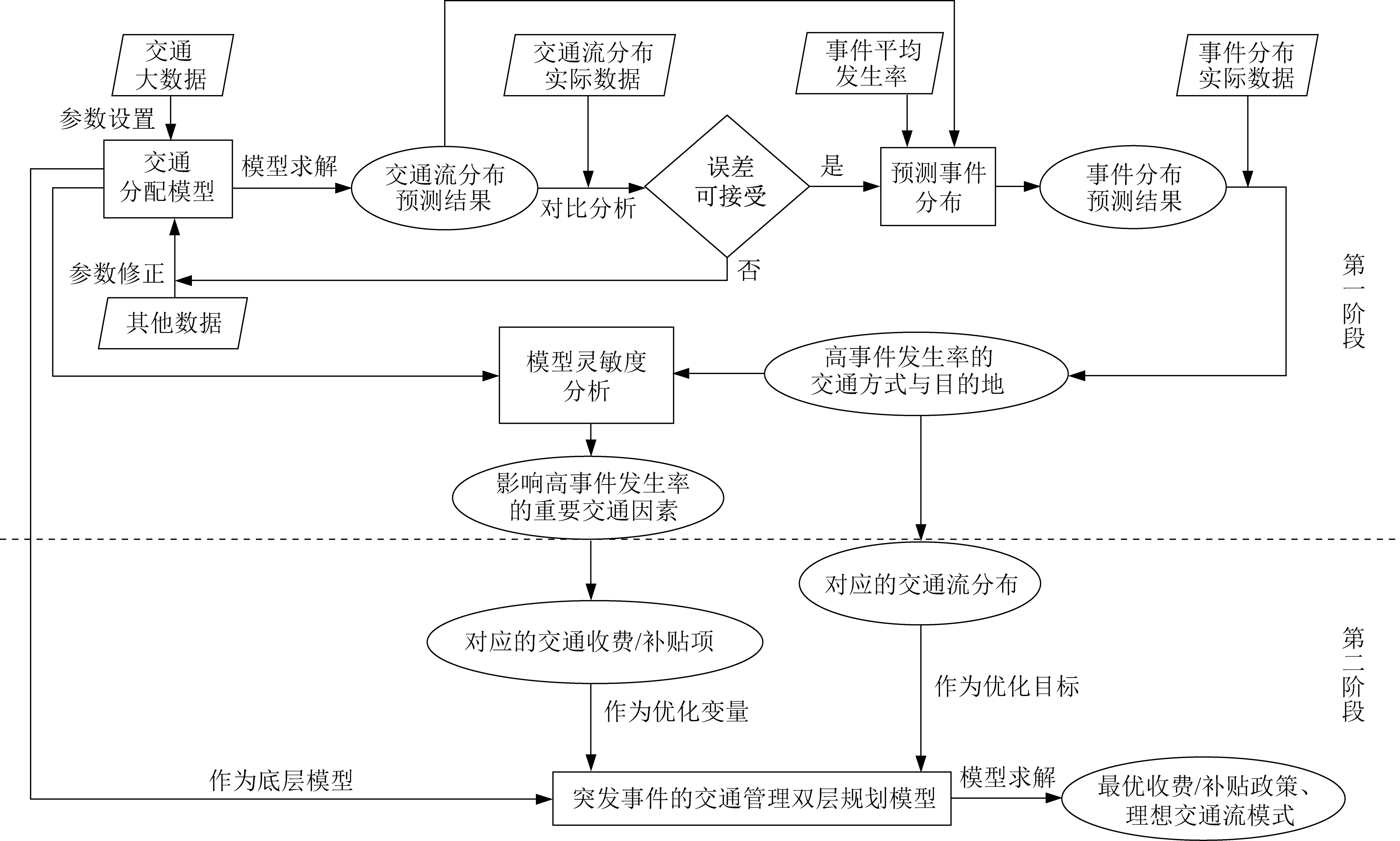
图1 公共卫生交通管理方法流程Fig.1 Flow chart of public health transportation management method

2.1 公共卫生交通管理方法第一阶段

（1）步骤一，模型选择。根据突发公共卫生事件下交通系统及出行群体的特点，选择合适的交通分配模型。

（2）步骤二，参数修正。结合同类型或相似类型突发公共卫生事件下的历史交通数据对交通分配模型参数进行修正，数据包括历史交通流分配数据以及与突发事件传播目的地相关的数据。

（3）步骤三，误差分析。利用修正后的交通分配模型预测历史突发公共卫生事件下的交通流分布，并对比预测结果与实际数据。若预测结果与实际数据相差较大，则收集更多的数据继续修正模型参数，直到接近实际数据。

（4）步骤四，模型判断。若参数调节无法改善模型预测性能，则选择其他交通分配模型：重复以上步骤直至获得理想的预测结果。

（5）步骤五，确定优化目标与交通管理参数。确定交通分配模型后，确定下一阶段交通应急管理的优化目标以及对优化目标有重大影响的交通管理参数。将模型计算得到的交通流分布结果与实际突发公共卫生事件下的交通流分布作对比，找到与实际情况误差较大的交通流分布结果。例如，某种交通方式下的交通流分布预测结果或某地区的交通流分布预测结果明显低于实际值，说明该交通方式下或该地区的公共卫生事件感染风险要高于平均水平，可以作为下一步需要优化的目标。明确与交通管理措施相关的交通管理参数，如与高铁交通管理相关的高铁票价，与高速公路交通管理相关的高速公路收费价格等。在此基础上，对优化目标进行不同交通管理参数的灵敏度分析，找到对优化目标影响最大的交通管理参数，并确定该参数所对应的交通应急管理措施，如与高铁票价对应的管理措施为调节高铁票价，即提高或降低价格。

2.2 公共卫生交通管理方法第二阶段

（1）步骤一，构造双层规划模型。在第一阶段分析结果的基础上，构造突发公共卫生事件的交通应急管理双层规划模型。上层模型优化变量为第一阶段确定的交通管理参数，上层模型优化目标为第一阶段确定的与突发公共卫生事件传播强相关的不同类型交通需求；下层模型为第一阶段确定的交通分配模型。

（2）步骤二，双层规划模型计算。通过求解该双层规划模型可以得到最优交通应急管理决策。

3 武汉迁徙人口的交通流分布预测

3.1 预测模型

3.1.1 多方式出行成本函数

考虑5种主要出行方式，即私家车出行方式、高铁出行方式、普通火车出行方式、长途客车出行方式和飞机出行方式。多方式交通出行成本函数的相关参数值是从连接武汉与其他城市的实际交通网络中获得的经验数据。令Cd，m表示从武汉到目的地为d出行方式为m的出行成本（d∈D，m∈M，M=｛私家车，高铁，普通火车，长途客车，飞机｝）。目的地集合D包括湖北省内部分地级或县级城市（15个，不包括武汉）和中国除湖北省外的33个省级地区。将湖北省内15 个城市组成的集合定义为Din（Din=｛孝感，黄冈，荆州，咸宁，鄂州，襄阳，黄石，荆门，随州，仙桃，宜昌，天门，十堰，恩施，潜江｝），33个省级地区组成的集合定义为Dout（Dout=｛河南，湖南，安徽，江西，广东，江苏，重庆，四川，山东，浙江，河北，福建，北京，广西，陕西，上海，山西，贵州，云南，海南，甘肃，辽宁，黑龙江，新疆，内蒙古，吉林，天津，宁夏，青海，西藏，香港，澳门，台湾｝），则D=Din∪Dout。

从武汉到各目的地使用不同交通方式出行的成本函数如下：

（1）私家车出行方式

式中：εat为每公里消耗的汽油成本；ld为驾驶私家车从武汉到目的地d的公里数；Td，at为乘坐私家车的出行时间；vat为乘坐私家车的单位时间货币价值，将出行者的出行时间进行货币化可得到出行时间成本，即出行时间的货币价值；Fd，hw为高速公路通行费成本；Cd，at为乘坐私家车的出行成本；n为私家车平均载客数。成本函数由三项组成：第一项为乘坐私家车出行时间的货币价值；第二项为本次出行所消耗的汽油成本；第三项为高速公路通行费成本，可由我国高速公路每公里平均收费金额与高速公路总路程长度的乘积计算得到。考虑私家车平均载客数对私家车出行效用的影响。私家车平均载客数n是指一辆私家车的平均乘员数。武汉市交通运输局公布的数据显示，武汉市私家车的日常平均载客数为1.8人·辆−1。此外，来自湖北省春运办的报道，近几年春运期间出行方式出现了从公共交通向私家车转移的现象。亲友共同分担出行费用以及较大的行李空间、无需换乘等优势吸引了越来越多的个人乘坐私家车返乡。因此，假设春运期间，武汉市私家车平均载客数不低于日常平均载客数（1.8 人·辆−1），n的值取2。

（2）高铁出行方式

式中：Td，hr为乘坐高铁的出行时间；vhr为乘坐高铁的单位时间货币价值；Cd，hr为乘坐高铁的出行成本；τd，hr为高铁票价。乘坐高铁的出行成本由两项组成：第一项为乘坐高铁出行时间的货币价值，第二项为高铁票价。

（3）普通火车出行方式

式中：Td，r为乘坐普通火车的出行时间；vr为乘坐普通火车的单位时间货币价值；Cd，r为乘坐普通火车的出行成本；τd，r为普通火车票价。乘坐普通火车的出行成本由两项组成：第一项为乘坐普通火车出行时间的货币价值，第二项为普通火车票价。

（4）长途客车出行方式

式中：Td，c为乘坐长途客车的出行时间；vc为乘坐长途客车的单位时间货币价值；Cd，c为乘坐长途客车的出行成本；τd，c为长途客车票价。乘坐长途客车的出行成本由两项组成：第一项为乘坐长途客车出行时间的货币价值，第二项为长途客车票价。

（5）飞机出行方式

式中：Td，f为乘坐飞机的出行时间；vf为乘坐飞机的单位时间货币价值；Cd，f为乘坐飞机的出行成本；τd，f为飞机票价。乘坐飞机的出行成本由两项组成：第一项为乘坐飞机出行时间的货币价值；第二项为飞机票价。

3.1.2 多模式交通网络均衡模型

考虑目的地与交通出行方式的双重选择，提出了一个多模式交通网络随机用户均衡模型，如下所示：

约束条件：

式中：θd为与前往目的地d的交通出行方式选择相关的阻抗参数；δ为与目的地选择相关的阻抗参数；βd，m为前往目的地d的交通出行方式m的吸引力参数；αd为目的地d的吸引力参数；qd，m为前往目的地d的交通出行方式m的交通需求；qd为前往目的地d的交通需求；Q为总出行需求。为量化每个目的地对武汉的吸引力，定义了目的地吸引力的加权函数，如下所示：

式中：Hd为归一化后目的地d的历史需求分布比例；Pd为归一化后目的地d的人口数量；Ld为归一化后目的地d与武汉之间的距离；a为参数Hd的加权系数；b为参数Pd的加权系数；kd为参数Ld的加权系数。加权系数a、b、kd反映了历史需求分布比例、人口数量、与武汉之间的距离这3个因素对目的地d吸引力的影响程度。从实际生活经验可以观察到：目的地d的历史需求分布比例Hd往往与其到出发城市的出行距离Ld成反比。参考式（17）可知，从武汉到目的地d的广义出行成本ud与出行时间成正比，而出行时间又与广义出行距离Ld正相关，因此从武汉到目的地d的广义出行成本ud与出行距离Ld成正比。为了消除出行距离Ld对广义出行成本ud和历史需求分布比例Hd的影响，将历史需求分布比例相关项aHd乘以出行距离Ld的修正系数kd。

标记目的地d的历史需求分布比例、人口数量和出行距离的原始数据为hd、pd、ld。由于hd、pd、ld分别是由不同计量标准得到的数值，因此不能直接相加，需要进行归一化处理。归一化后的历史需求分布比例、人口数量和出行距离计算式如下所示：

式中：min(·)函数用于获取列表中最小项；max(·)函数用于获取列表中最大项。由式（14）可知，0 ≤Ld≤1，则对于任意kd（kd＞0），加权距离Lkdd的取值范围在0 到1 之间。出行者的感知偏差也会对出行者的行为产生影响，如短途出行者对出行成本的敏感度要普遍高于长途出行者，这一心理现象已经在随机交通流分布领域得到了深入研究［14］。由此可以认为，湖北省内的出行者比湖北省外的出行者对出行成本更为敏感。相应地，省内出行者对目的地吸引力的感知程度大于省外出行者，对于目的地吸引力计算，就需要满足（d∈Din)＞Lkdd（d∈Dout)。已知0 ≤Ld≤1，因此k（dd∈Din）＞kd（d∈Dout)。在武汉市春运期间，流动人口构成出行需求的主体，历史交通流分布信息可以为以后的交通流分布预测提供重要的参考依据。突出历史交通流分布信息对目的地吸引力估计的重大影响，设定与历史需求分布比例相关的加权系数大于与人口数量相关的加权系数，即a＞b。相关参数值如表1所示。式（6）～（10）描述了基于双层嵌套Logit 选择模型的随机用户均衡问题。式（6）为目标函数；式（7）为出行总需求守恒约束，确保分配到武汉市内不同目的地的交通流量总和等于总出行需求Q，2019 年武汉市春运期间总出行需求Q为5 000 000；式（8）为目的地需求守恒约束，保证分配到某目的地的不同交通出行方式的交通流量总和等于从武汉到该目的地的交通需求；式（9）和（10）要求目的地需求和交通出行方式需求满足非负条件。

表1 基于嵌套Logit的交通分配模型相关参数Tab.1 Parameters for nested-Logit-based traffic assignment model

通过该随机用户均衡问题的一阶条件可以得到关于交通出行方式选择和目的地选择的双层嵌套Logit模型，如下所示：

此随机用户均衡问题的求解分两步：首先根据式（17）计算目的地广义出行成本ud（∀d∈D），然后按照交通流分配原则（15）与（16），求得目的地需求和交通出行方式需求，即qd、qd，m。

3.2 预测结果分析

新冠肺炎疫情爆发后不久，共有500 多万人离开武汉。利用第3.1节中提出的交通分配模型分析武汉市500万人的迁徙去向。将人口出行分布分为两部分：一部分从武汉市到湖北省其他城市，属于省内出行；另一部分从武汉市到其他省市，属于省外出行。

为了方便计算式（11）中的参数Hd，采用武汉市到其他省份省会城市的出行效用统一代表到该省其他城市的出行效用。利用腾讯社交网络春节地理定位数据平台收集到的2017 年武汉向其他目的地迁移的数据，除河南、安徽、湖南、江苏、浙江、广东等省份外，武汉市到其他省级地区的交通流量大部分集中在该省的省会城市，因此在计算式（11）中的参数Pd时，采用省会城市的人口数量来代替该省的人口数量。对于河南、安徽、湖南、江苏、浙江、广东这6个省，则采用该省2017年武汉市外来人口最多的几个城市的人口总和来代替该省的人口数量。

式（11）中的出行距离Ld采用从武汉到各目的地的公路长度。根据日常出行经验，各交通工具出行时间货币价值的设置遵循vf＜vhr＜vat＜vr＜vc。此外，还考虑了不同种类的出行者对于出行成本的感知偏差，相关研究结果［14］表明，短途出行者比长途出行者对出行成本更为敏感，设定θd，m的值在∀d∈Din情况下是∀d∈Dout情况下的5倍。

3.2.1 交通流分布预测结果分析

利用第3.1节中提出的交通分配模型计算得到武汉市到其他48个目的地（包括湖北省内15个城市和33 个省外目的地）的交通流量。另外，从百度迁移大数据平台收集到了2019 年春运期间武汉市实际的迁徙分布数据，用以分析预测误差。图2 为所有目的地交通流量的预测值与实际值对比。预测得到孝感、黄冈、荆州、咸宁、鄂州是湖北省内迁徙人数最多的5个城市，河南、湖南、安徽、江西是湖北省外迁徙人口最多的4 个省份，这与实际情况保持一致。

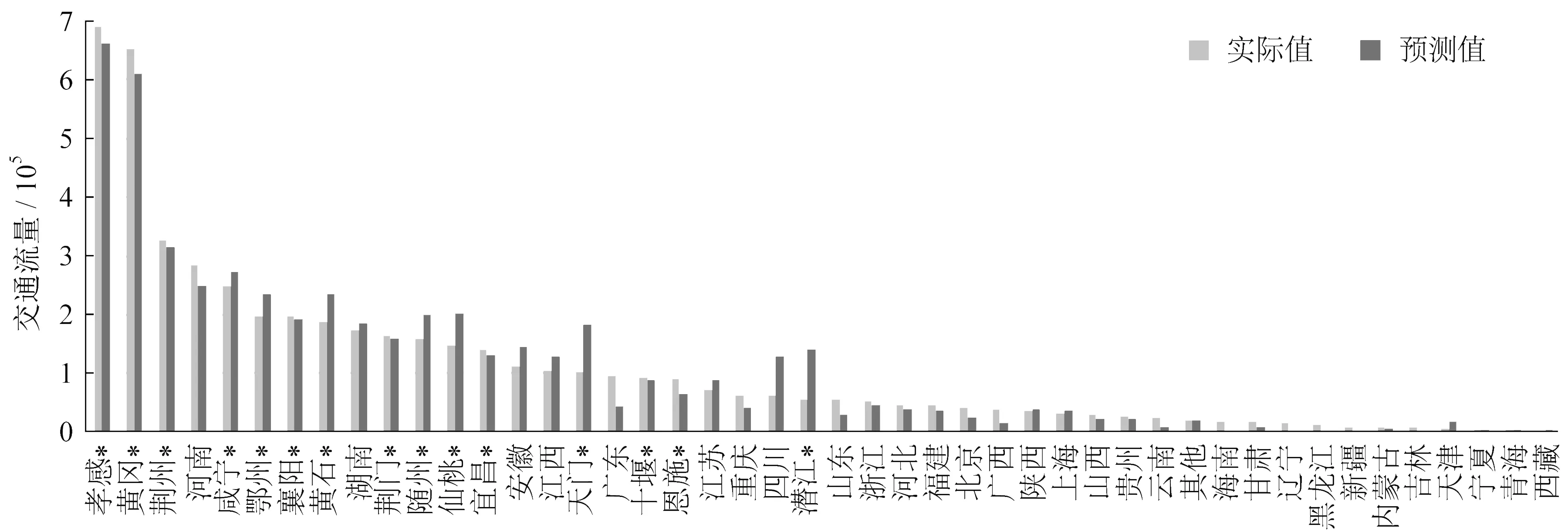
图2 交通流量的实际结果与预测结果对比Fig.2 Comparison of traffic volume between actual and estimated results

3.2.2 疾病传播预测结果分析

根据国家卫生健康委员会官方报道，从2020 年3 月18 日开始中国新增确诊病例均为境外输入，因此将2020 年3 月18 日当天统计到的确诊病例数作为此次国内疫情传播的最终确诊病例数。定义从武汉离开的出行者的平均发病率

式中：z为除武汉外的全国确诊病例数。已知z=31 296，可以得到γ=0.625 9%，再利用计算式qdγ（∀d∈D）进一步预测不同目的地的发病人数。

图3为不同地区新冠肺炎发病人数的实际值与预测值对比。可以观察到，模型的预测结果高估了湖北省内大部分城市以及河南、湖南两省的发病人数。在第3.2.1 节的交通流预测结果中，这些城市或省份是预测交通流量分布最多的目的区域。这说明湖北省内以及河南与湖南两省的实际发病率要低于平均发病率。中国政府在此低发病率现象背后发挥了重要作用。为防止疫情传播扩散，中国政府采取的有效防控措施包括：疫情发生后立即对湖北省内12个城市的公共交通实行阻断；在湖北省内建设临时治疗中心，如方舱医院等；其他省市对来自武汉的出行者实行为期两周的强制性自我隔离；指定并实施以社区为单位的疫情防控管理制度；所有紧缺物资实行国家统一调度，如调度医务人员和医疗设备到医疗资源匮乏地区等。此外，模型的预测结果低估了包括广东、重庆、四川、山东、浙江、北京、上海、黑龙江、香港、澳门等在内的目的地的发病率。原因可能是大部分以上地区的商业活动较为频繁，而商业活动过程中人与人的亲密接触会增加感染新冠肺炎的风险，导致发病率的上升。此外，黑龙江省感染人数较多很大程度上与聚集性活动中的病毒传播有关［15］。

图3 发病人数的实际结果与预测结果对比Fig.3 Comparison of patient number between actual and estimated results

3.2.3 不同交通出行方式需求分布预测结果分析

为了遏制新冠肺炎的大规模传播，对武汉乃至几乎整个湖北省的公共交通系统实施了阻断。在此背景下，研究特定交通出行方式限制政策对武汉迁徙人口分布的影响具有十分重要的意义。由表2可知，对某一交通出行方式的阻断将导致其他出行方式交通流量的增长，其中阻断高铁出行方式对其他出行方式交通流量增长的影响最为显著，因此在阻断高铁出行方式的情况下应加强对其他公共交通方式的疫情防控工作。研究还表明，对某一交通出行方式阻断导致的其他出行方式的交通需求量增长是不同的。例如，在湖北省内实施普通火车出行方式阻断对于私家车出行交通需求量的增长影响最大（增长63.65%），而对私家车出行方式实施限制则会导致长途客车出行出现最大增长率（增长42.98%）。对与某交通出行方式阻断高度相关的其他公共交通方式加强管理，可以降低病毒通过这些公共交通出行方式大规模传播的风险。

表2 某交通出行方式阻断下其他交通出行方式的需求增长Tab.2 Demand growth of the other traffic patterns when applying lockdown on one traffic pattern

3.2.4 模型的灵敏度分析

对交通管理参数（包括高速公路通行费成本（Fhw）、高铁票价（τhr）、普通火车票价（τr）、长途汽车票价（τc）、飞机票价（τf）和私家车平均载客数（n））进行灵敏度分析。通过鼓励交通流从公共交通方式转向私家车出行，将降低突发疫情通过公共交通传播的风险。表3 中，Qat为私家车出行方式交通需求总量。由表3可见，n（私家车平均载客数）的增加对Qat值提升的正面影响最大，其次是提升τhr（高铁票价）。

第3.2.2 节的研究结果表明，经济发达地区以及大型聚集性活动频繁地区的社交接触多、疾病传播风险较高，抑制这些目的地的交通需求也是防止病毒大规模传播的有效途径之一。定义Qhi为高社交接触频率地区的总出行需求。表3 中列出了Qhi对不同交通管理参数的灵敏度。利用Qhi关于各交通管理参数的灵敏度信息识别出能够引发Qhi负增长的交通管理参数。本研究中，n的减少导致Qhi的下降最快，增加τhr的效果紧随其后，这表明降低私家车平均载客数和提高高铁票价是抑制武汉到高风险目的地交通出行的有效途径。注意到减小n的同时Qat下降，这与促进私家车出行方式需求量增长的初衷相悖，应当考虑到这种矛盾的存在，对交通管理参数进行合理设置。

表3 Qat与Qhi关于各交通管理参数的一阶导数Tab.3 Derivatives of Qat and Qhi with respect to different input parameters

4 控制疫情传播的交通收费与补贴方案设计

4.1 方案模型

采用对省外出行者发放共享出行补贴提高省外私家车平均载客数、提高省外高铁票价以抑制省外高社交接触频率地区的出行总人数2种方法。目前关于如何发放共享出行补贴尚在研究和摸索阶段［16-17］，假定由政府或共享出行相关运营企业向省外共享出行的私家车乘客每人发放固定金额的共享出行补贴，以实现期望达到的省外私家车平均载客数水平，并约束省外共享出行补贴总金额不超过由省外高铁票价上调带来的财政总收入。构建一个双层规划模型，上层模型的优化变量为省外私家车平均载客数增量（Δnout）以及省外高铁票价上调金额（Δτhr）。

考虑省外私家车平均载客数增量Δnout对私家车出行成本函数的影响，计算式如下所示：

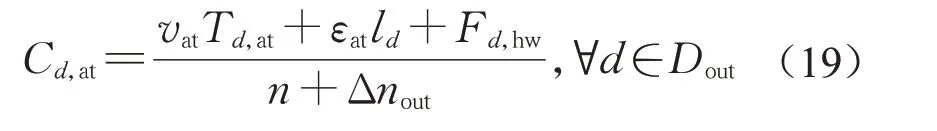
考虑省外高铁票价上调金额Δτhr对高铁出行成本函数的影响：

Cd，hr=vhrTd，hr+τd，hr+Δτhr，∀d∈Dout（20）

上层模型的优化目标是提高省外私家车出行人数的同时减少高社交接触频率地区的交通总需求。将均衡状态下省外私家车出行总需求用Qˉout，at表示，均衡状态下高社交接触频率地区交通总需求用Qˉhi表示，计算可得Qˉout，at=261 451，Qˉhi=260 003。为了方便对2 个指标进行综合评价，将对省外私家车出行总需求及高社交接触频率地区的交通总需求进行标准化处理，使2 个指标处于同一数量级。将省外私家车出行总人数及高社交接触频率地区的交通总需求与各自在均衡状态下值的比值作为衡量系统性能的指标。α为高社交接触频率地区交通总需求的修正系数，取值为高社交接触频率地区的平均感染率与全国其他地区（不包括武汉）的平均感染率的比值，参考相关数据可以得到α=5.5。以各指标加权总和最小为上层模型优化目标，将λ作为加权因子，可以得到上层数学规划模型，如下所示：

式中：Δτhr，max为Δτhr的上限，取50；Δnout，max为Δnout的上限，考虑私家车规格最小为四人座，在原来平均载客数2 人的情况下，最大私家车载客数增量为2，即Δnout，max的值为2；ρ为预先规定的每个共享出行乘客的补贴，设定为20。约束条件（24）限定省外共享出行补贴总金额不超过省外高铁价格上调带来的财政总收入。

上层模型可以解释为寻找一个方案T=(Δnout，Δτhr)，使得高社交接触频率目的地出行人数尽可能低，同时省外私家车出行人数尽可能高，2 个目标的相对重要性通过λ的大小体现。目标函数（21）中的未知数Qhi、Qout，at可由下层模型获得，下层模型即为交通应急管理下的随机用户均衡模型。通过求解该双层规划模型，即可得到系统性能加权总和最小的交通应急管理方案。为求解提出的交通应急管理方案，首先将约束条件作为惩罚因子项附加到原上层模型的目标函数中，将上层模型转化为无约束的极值模型，然后利用模式搜索法求解上层模型，得到交通应急管理方案T=(Δnout，Δτhr)，最后用连续平均算法（MSA）求解下层模型，得到Qhi、Qout，at。

4.2 方案效果分析

将上层目标函数中高社交接触频率地区出行总人数目标权重λ从0 增加至1.0，不同权重系数下省外私家车出行总人数、高社交接触频率地区出行总人数、系统加权总目标值的变化情况如图4～6所示。

图4 系统最优时不同权重下的省外私家车出行总人数Fig.4 Total number of passengers out of Hubei Province in private car travel pattern under different weights when system is optimal

图5 系统最优时不同权重下的高社交接触频率地区出行总人数Fig.5 Total number of passengers in areas with high social contact frequency under different weights when system is optimal

图6 系统最优时不同权重下的系统加权总目标值Fig.6 Weighted target value of the system under different weights when system is optimal

可以观察到，以系统加权总目标值最小为目标实行最优交通应急管理时，当目标函数中高社交接触频率地区出行总人数目标权重λ从0 增加至1.0时，省外私家车出行总人数、高社交接触频率地区出行总人数呈下降趋势，系统加权总目标值呈上升趋势。当0 ≤λ≤0.7时，为使系统加权总目标值最小，需要满足省外私家车出行总人数最多的同时高社交接触频率地区出行总人数最小。省外私家车出行总人数受私家车平均载客数影响最大，私家车平均载客数的增加会引发省外私家车出行总人数的提升。由于高铁收费与共享出行补贴平衡约束的限制（见式（24）），私家车平均载客数最大增长幅度为0.7（Δn*out=0.7），因此随着λ值从0 增大到0.7，私家车平均载客数满足最大值2.7。同时，由于私家车平均载客数的上升对于高社交接触频率地区出行总人数也有促进作用，为了使高社交接触频率地区出行总人数最少，需保持高铁收费金额为最大值50元。将λ从0.7继续增大，高社交接触频率地区出行总人数对目标函数值影响较大，为使目标函数值最小，需要满足高社交接触频率地区出行总人数最小的同时省外出行总人数尽量最大。由于高社交接触频率地区出行总人数与私家车平均载客数负相关，因此私家车平均载客数增幅最小值为0（Δn*out=0），这也间接导致了省外私家车出行总人数最低，在此基础上向省外高铁乘客征收最大高铁收费金额（Δτ*hr=50）可以最大程度抑制省外出行人数。因此，当λ在［0.7，1.0］范围内时，高社交接触频率地区出行总人数与省外私家车出行总人数均达到最小值，分别为240 010与328 972。同时，由于λ的增大导致高社交接触频率地区出行总人数及省外私家车出行总人数递减，并且省外私家车出行总人数减少的幅度大于高社交接触频率地区出行总人数减少的幅度，这会导致系统加权总目标值递增。在实际交通应急管理政策中，需根据一定的目标设定合理的管理决策值（Δnout，Δτhr）和λ值。

5 结语

将交通大数据与交通分配模型、交通优化理论相结合，提出一种公共卫生交通管理方法。第一阶段利用随机交通分配模型分析突发公共卫生事件在交通网络中的传播即分布情况，识别出需要管控的交通性能指标以及影响这些交通性能指标的交通因素；第二阶段构建一个双层规划模型，上层变量为交通收费或补贴，优化目标为第一阶段分析出的需要管控的交通性能指标，最后得到最优收费补贴决策。数值模拟结果表明，病毒的传播与交通流分布不成线性关系。这是由于疾病的蔓延不仅取决于交通状况，还受政府防控力度以及地区经济活动的频度、人群聚集活动次数的影响。对某一种交通出行方式进行阻断会引起其他交通出行方式需求量不同程度的变化，阻断高铁出行方式对其他出行方式的交通流量变化的影响最明显，因此了解某一种交通出行方式阻断行为与其他交通出行方式需求变化之间的关联度是非常重要的。此外，灵敏度分析结果表明，对疫情交通传播有重要影响的交通管理参数为私家车平均载客数以及高铁收费金额。最后，通过双层规划模型得到控制疫情传播的最优高铁票价、最优私家车平均载客数以及共享出行补贴等交通管理方案。

作者贡献声明：

郑 煜：提出选题，设计论文框架，构建模型，分析数据，撰写并修订论文。