基于CFD模拟及PIV技术的鱼池流场分析与优化
2022-06-06张成林张宇雷郑跃平
张成林,张宇雷,吴 凡,吴 铠,郑跃平
(1 中国水产科学研究院渔业机械仪器研究所,农业农村部渔业装备与工程技术重点实验室,上海 200092;2 青岛海洋科学与技术国家实验室深蓝渔业工程装备联合实验室,山东青岛 266237;3 上海市水生野生动植物保护研究中心,上海 200092)
鱼池作为水产养殖尤其是循环水养殖系统中最基本也是极为重要的一个生产单元,其形状、尺寸、结构对养殖产量、养殖效率及后期维护费用有着很大的影响,尤其是鱼池的水流特性,直接关系到鱼类生长的最佳流态,因此,通过现代科技手段对其流场进行详细分析测量,探索优化流动环境是循环水高密度养殖的前提条件。
鱼池设计主要考虑建设成本、空间利用、水质维护及便于管理等因素[1],常用形状有圆形、矩形(方切角)等。圆形鱼池水体流动情况较好,方便自行集排污,但土地利用率不高且流速不能准确预测[2-3];矩形鱼池易于建设,土地利用率高,但池中会出现死水区,水体交换不均匀,造成局部缺氧或代谢废物集中于死水区[4]。由此可见,如何准确地设计鱼池的形状及结构,使其内部水流流速分布均匀、水体交换完全、不存在运动死角、集排污效果好,对陆基高效全循环水养殖工程有重要意义。
目前,国内对于鱼池内水体流态的研究仍较少,主要是缺少研究方法和手段。国外方面,研究主要集中在对于鱼池流态流场的描述方面。Joan等[5]使用ADV(Acoustic Doppler Velocimeter)测量了鱼池内不同深度,不同半径处的水流切向速度,提出鱼池内的水体是由自由涡和强制涡组成的组合涡形态。湛含辉等[6]研究提出利用二次流理论来实现池内颗粒污染物的快速收集,但是由于涉及边界层、涡流现象等问题,在定量研究方面存在较大的难度。此外,在鱼池进水方式及流速控制的调研中,有研究表明,鱼池内部水体的旋转速度从池壁到池中心,从池表面到池底都要尽可能地保持一致,它可保证鱼池完成自清洗,但速度不应过大,避免能量浪费。水流速度为鱼体长度的0.5~2.0倍/s,有利于鱼类生长,要求推动可沉淀固体颗粒物到池中心的速度应大于15~30 cm/s[7-9]。由此可见,在鱼池的设计中,除结构参数外,应着重研究进水口位置的布置及进水流速的控制[10-12]。
鱼池形状及结构的研究可分为传统经验方法和数学方法两类。传统经验方法主要依靠常年积累的养殖经验,该方法存在一定的主观性,多限于小范围的定性研究;数学方法主要是指利用物理数学模型进行计算机模拟的方法,习惯上称为计算流体力学方法(Computational Fluid Dynamics,CFD),是当前的一种非常有效的研究方法,其在水体的流动特性研究方面得到了广泛的应用[13-15]。粒子图像测速(Particle Image Velocimetry,PIV)技术作为一种先进的全流场、瞬态、无接触测量技术,可将测得的数据和控制相间动力学特性的物理机理联系起来[16],对部分通过CFD方法得出的模拟结果进行流态验证。在CFD方法与PIV技术相结合解决实际问题方面,国内外尚无将其应用到鱼池相关问题的研究上,但在人工鱼礁水动力学及螺旋分离器水流动特性研究方面均有涉及[17-18],其采用三维湍流模拟技术为手段,开展了水动力学的数值模拟研究,同时与动力水槽试验,特别是PIV技术的实测结果进行对比分析,使两类方法得到相互验证。
以鱼池作为研究对象,采用CFD模拟与PIV技术相结合的手段,研究在不同循环率及进水流速下的鱼池流场特性,同时进一步研究进水口位置变化对鱼池流场的影响,以期为今后鱼池的结构建造与优化提供研究手段及理论依据。
1 鱼池结构与参数设计
1.1 鱼池结构
本研究选用的鱼池需符合:满足鱼类快速、健康生长需求;便于实现颗粒污染物的快速收集,保证养殖水质;满足操作性和经济性需求。以中国水产科学研究院渔业机械仪器研究所“农业农村部渔业装备与工程技术重点实验室”中的高密度循环水养殖鱼池为研究原型,其主要由3部分组成,分别为进水口、池体和出水口,主要参数为:池体直径2.0 m,水深0.8 m,鱼池总水体量约为2.5 m3,进水口中心线距离鱼池池壁0.1 m,鱼池池底坡度为3 %,即鱼池中心水深0.83 m,鱼池出水口直径为50 mm。固液混合液体以一定的初速度从进水口流入池体,而后经出水口排出。几何模型及尺寸如图1所示。
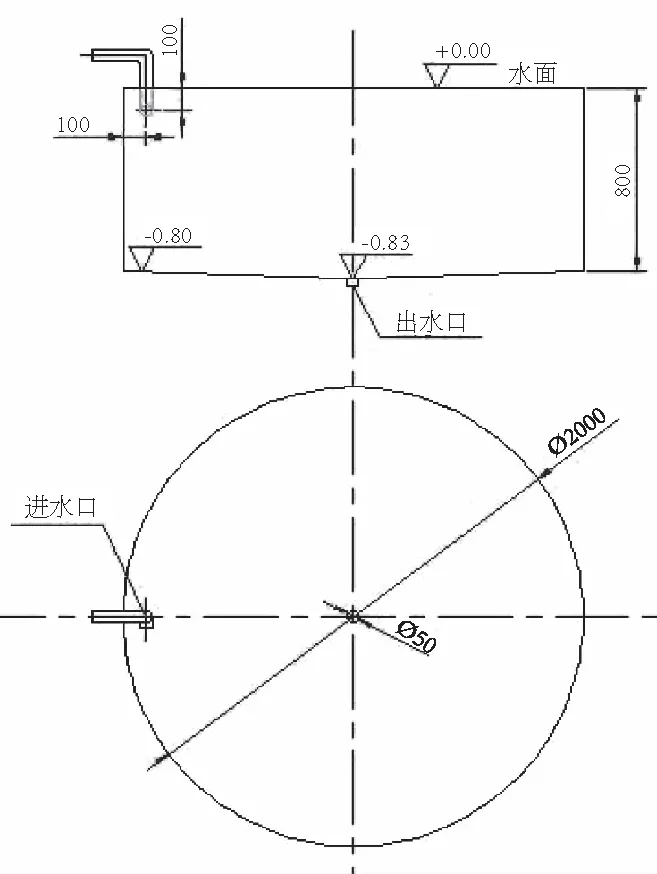
图1 鱼池几何模型
1.2 参数设计
选择对鱼池的循环率、进水口流速和进水口位置这3个关键设计参数进行模拟优化。根据Davidson等国内外相关学者对鱼池各项参数的研究与建议[19-21]以及循环水养殖系统的运行经验,初始运行参数设计如下:循环率设置2个梯度,分别为1次/h和2 次/h,对应循环量(Q)为800 L/h和1 200 L/h;鱼池进水速度(Vin)设置3个梯度,分别为1 m/s、2 m/s、3 m/s;进水口位置(H)设置为水面以下10 cm和30 cm。对各组参数分别进行计算机模拟研究与分析,具体参数详见表1。
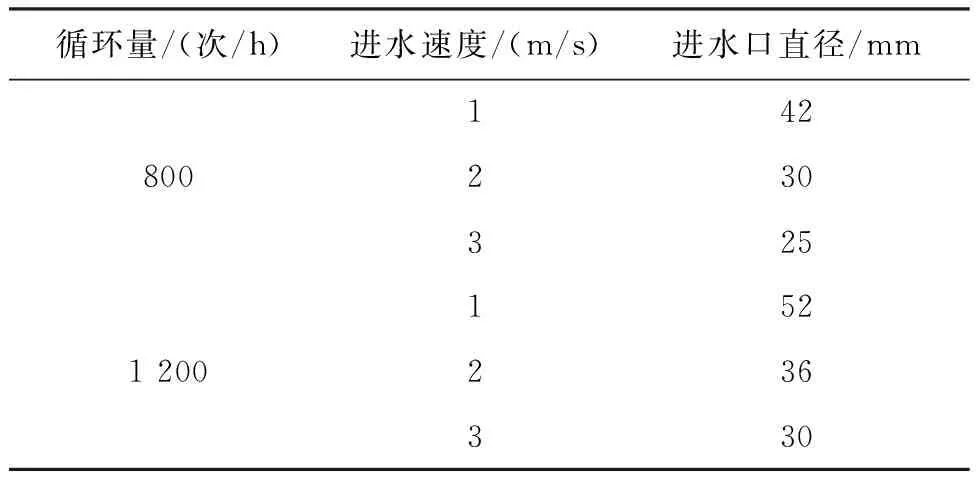
表1 鱼池结构及运行参数
2 数值模拟与PIV流场测试
2.1 数值模拟
2.1.1 数学模型
用ANSYS Fluent 16.1软件和联想服务器进行数值模拟。考虑到鱼池流场特性,首先可将鱼池流场视为等温、不可压缩三维流场;其次,鱼池出水流量由进水流量控制,当鱼池流场发展充分后,在进水流量不变的前提下,鱼池中各点的速度、压力等参数为常量,即其流场流动状态不随时间变化而变化,可按定常流动求解。故选择非耦合、隐式定常的3D求解器,采用N-S方程配合标准k-ε双方程紊流模型对鱼池进行三维数值模拟[22]。运用SIMPLE算法求解压力-速度耦合,动量、能量、组分、湍动能和湍流耗散率的离散格式均取一阶迎风差分格式,壁面附近采用标准壁面函数方法处理。设定残差监视器,当计算残差小于10-5时认为计算结果达到收敛。
标准k-ε模型是由 Launder 等[23]于 1972 年提出的,其双方程模型是通过补充微分方程的方法来获得紊流尺度的,用来封闭雷诺方程的微分方程数如下[13,24]:
GK-ρε
(1)
(2)
式中:GK为平均速度梯度引起的湍动能k的产生项,定义为:
(3)
式中:t为时间,s;xi为横坐标量,m;xj为纵坐标量,m;k为湍动能,m2/s2;ε为扩散率,m2/s;μ为水的运动黏性系数,m2/s;μt为水的涡黏系数,m2/s;σK和σε分别表示与湍动能k和耗散率ε对应的普朗特常数,C1ε和C2ε均为经验常数。根据经验公式模型的相关参数取值如下:C1ε=1.44,C2ε=1.92,μt=0.09,σK=1.0,σε=1.3。
2.1.2 网格划分与边界条件
利用GAMBIT建模平台构建鱼池三维模型,并结合鱼池模型形状进行网格划分及边界条件设定。在网格划分中,高质量的网格是完成模拟的前提,但同时又要避免因网格过密造成计算量过大。通常,网格质量以满足要求为准,即随着网格数目的增加,计算结果不再有显著的变化即可[25]。根据上述原则,本试验模型主要划分为六面体结构性网格,并将进水口和出水口区域进行网格加密操作,同时进行了网格独立性检验,最后确定的整体计算域网格数量为195 483个,具体划分见图2;选择非耦合、隐式定常的3D求解器,运用SIMPLE算法求解压力-速度耦合,动量、能量、组分、湍动能和湍流耗散率的离散格式均取一阶迎风差分格式,壁面附近采用标准壁面函数方法处理。在边界条件设定中,进水口选择速度进口,出水口设定为压力出口。

图2 网格划分
2.2 PIV流场测试
2.2.1 试验系统
为准确获取不同水流工况下鱼池的瞬时流场图像,搭建了流场测试试验系统。该试验系统主要包括光学补偿鱼池、水泵、流量计、控制装置和PIV系统,PIV系统主要部件及参数为:LaVision激光器,激光能量为2×135 mJ,最大频率为15 Hz;LaVision VC10-0090 CCD相机,分辨率为 1 936×1 216,最大频率为20 Hz;高分辨率8通道同步器。
2.2.2 匹配原则
PIV粒子图像测速主要基于基本模式匹配[26-27],其通过激光光源照射所测流场区域,形成流场光照平面,同时利用高速CCD摄像机同步获取示踪粒子的运动轨迹图像,并记录相邻两张图像I1和I2的时间间隔t,通过I1和I2中同一示踪粒子的位移与时间t的比值计算速度场,位移方向即为速度矢量。大量粒子的流动成像即可形成速度矢量场。其基本计算公式如下:
(4)
式中:m,n为对应粒子数。
在鱼池模型匹配方面,考虑到PIV拍摄镜头的大小,要对研究对象鱼池进行流场实测可行性较差,故采用制作缩尺模型的方法来拍摄实际流场。考虑到鱼池流场特性,动力源主要来自进水口,依靠水体黏性力带动鱼池水体整体流动。而且本试验模型进水口位于液面以下,基本不会在水面产生波浪,故选择雷诺数相似能够保证鱼池模型与原型的流动相似性,亦可更加准确地反映小型流场的流动特性。
2.2.3 试验方法
水源为自来水,示踪粒子选择聚苯乙烯颗粒,直径在60~100 μm之间,示踪粒子的数目以保证鱼池被测区域内粒子分布均匀为宜。试验系统搭建完成以后,连接好鱼池模型的循环管路,向鱼池内注入自来水并加入示踪粒子,然后水泵通电,通过流量计将进水速度调整到所需数值,使鱼池水体流动一段时间,流态基本稳定后调节摄像机镜头,使焦距对准中心点,使镜头轴线与反应器成90°角,待光线最佳、流态稳定后打开摄像系统,通过调整摄像机的光圈、快门速度、曝光强度、焦距等参数,使拍摄效果达到最佳,在确认拍摄效果可以后将影像保存至硬盘中。对保存的影像进行处理,用计算机软件提取出图片中的示踪粒子运动轨迹并跟基于数值模拟的鱼池流态进行拟合。
试验使用PIV系统二维成像功能,根据激光照射及光学补偿等实际测量条件,共拍摄鱼池内4个不同深度水平面上的流速分布情况,以池底为基准分别为:h=140 mm、120 mm、80 mm和10 mm,通过对原始拍摄图像的分析,得到鱼池速度矢量场、颗粒物运动状态及鱼池涡量场等。
3 结果与讨论
3.1 模拟结果与分析
3.1.1 速度分布
在不同的进水条件下,速度变化规律类似:水流速度从池壁到鱼池中心呈减小趋势,在中间半径处达到最小值,而后朝着鱼池中心逐渐增加。但在较低的进水流速下,鱼池池壁与鱼池中心的水流速度变化较小。
在鱼池直径方向的剖面上,速度分布斜率持续变化,在靠近池壁处达到最大值,而在鱼池中心则为负值。速度斜率在距离鱼池中心1/3处有较大提升,尤其是在进水速度较大的试验条件下,此现象与圆形鱼池二次流的相关研究相吻合[6,28]。
在不同进水条件下,鱼池沿直径方向的速度分布如图3、图4所示。
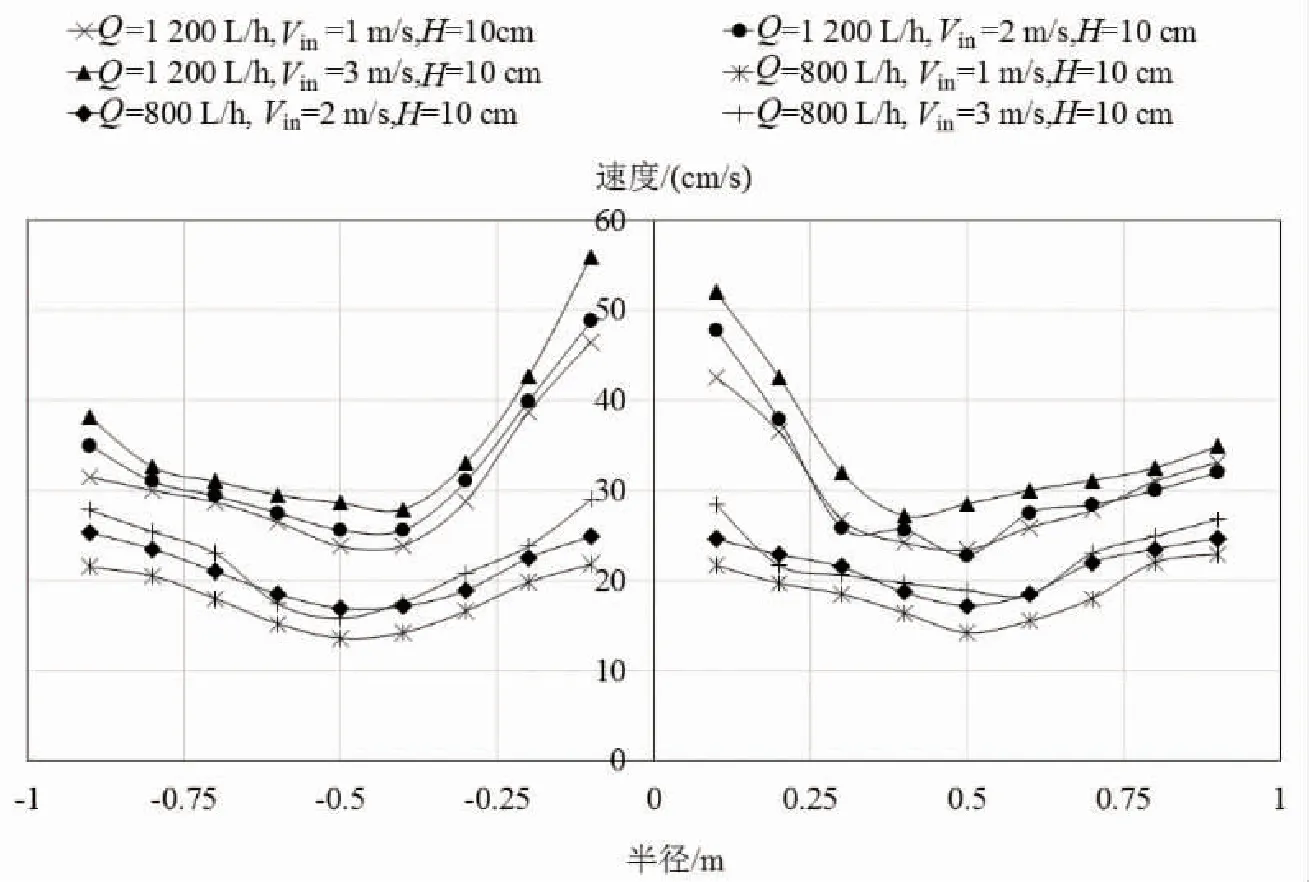
图3 不同进水条件下鱼池在直径轴上的速度分布(H=10 cm)
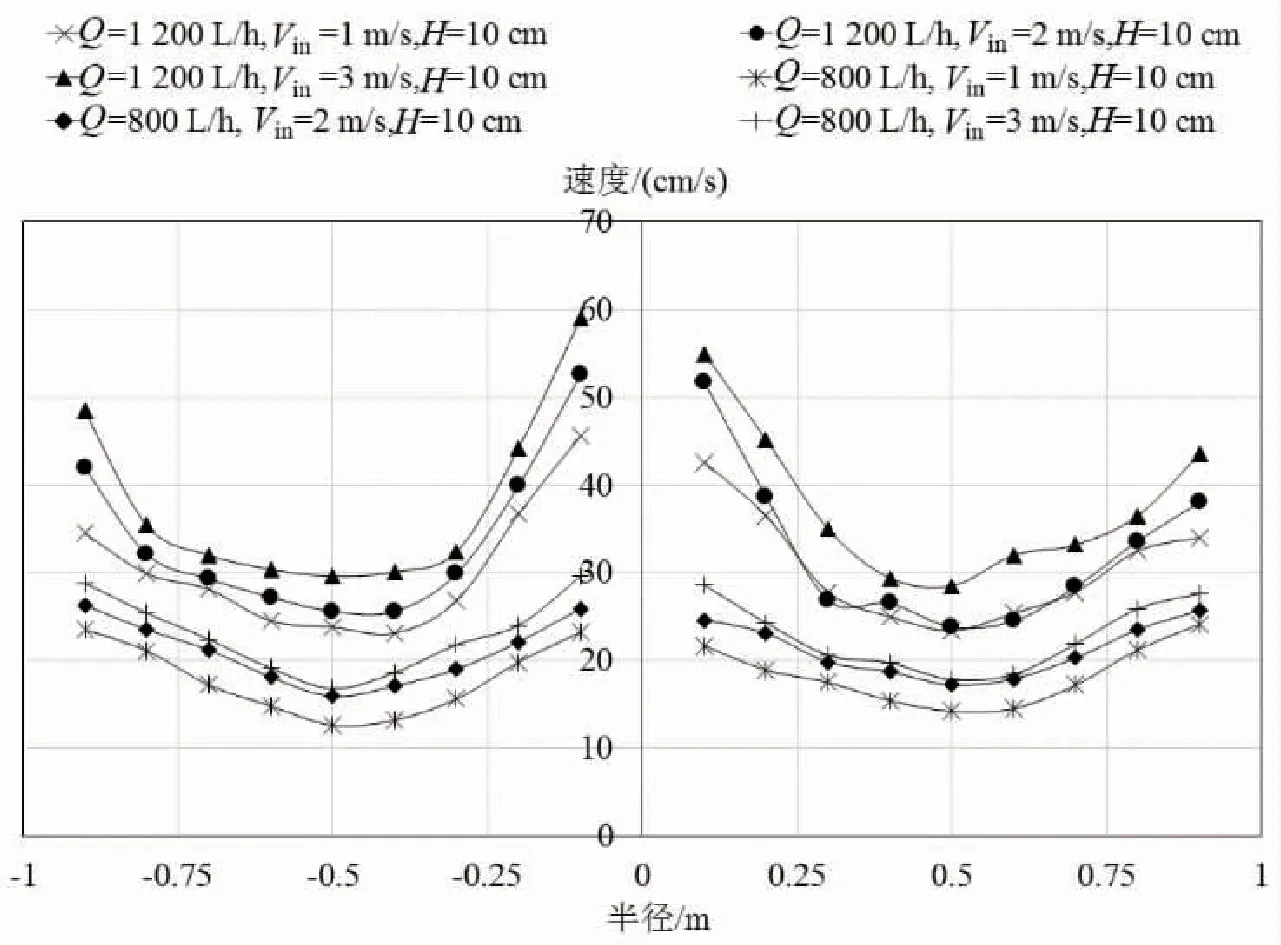
图4 不同进水条件下鱼池在直径轴上的速度分布(H=30 cm)
在相同的进水流量下,进水速度越快,鱼池整体流速分布越高,在池壁和鱼池中心处尤为明显,而进水口位置对鱼池内部流速分布影响差异性不显著(P>0.05)。
在相同的进水速度下,进水量越大(循环率高),鱼池整体流速分布越高,且进水量大使得鱼池中心流速显著高于靠近鱼池池壁附近的流速,但此现象在进水量小的试验条件下表现不明显。同样,进水口位置对鱼池内部流速分布影响差异性不显著(P>0.05)。
不同的进水口位置,会导致靠近鱼池池壁的流速有所不同,较深的进水口位置,其池壁附近的流速相对较快,但对鱼池整体流速分布影响甚微。
鱼池左右两个半径方向的流速分布并不完全对称,主要是受到进水口的影响,有进水口分布的一侧速度要高,但其差异在实验允许的误差范围之内,并不影响数值模拟结果,此结论与国外相关研究相吻合[29]。
3.1.2 流线分布与颗粒物运动轨迹
根据数值模拟的流场状态及流速分布情况,循环量Q为1 200 L/h时,鱼池流场的稳定性、均匀性及整体速度分布状态较好,以水体循环量Q为1 200 L/h时各工况下的流态模拟情况做主要分析。
当进水口位置在水面以下10 cm时,随时间发展的不同进水速度的鱼池流场流线图和固体颗粒物运动轨迹图(颗粒物直径设定为1 mm,密度为1.19 g/cm3,从进水口释放)见图5、图6。
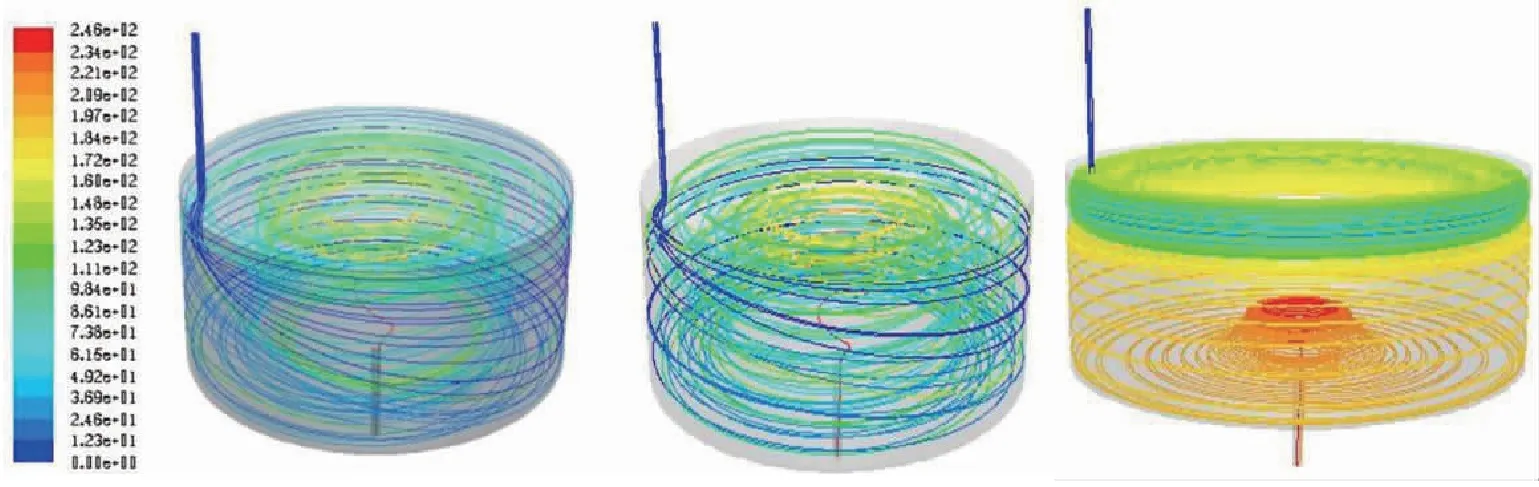
注:左1 m/s,中2 m/s,右3 m/s

注:左1 m/s,中2 m/s,右3 m/s
颗粒物运动轨迹与水流发展并不同步。在循环率不变且进水口位置固定的前提下,随着进水口水流流速的增大(进水口直径变小),鱼池中水体旋转速度变快,水流更容易也更迅速地流向出水口,但同时,由于快速旋转带来的离心力增大,颗粒物随着进水流速的增加,越来越集中的在池底做旋转运动,无法顺利运动到池底中心排出。由此可见,进水速度增大可以加快鱼池中水体旋转速度,但无法促进鱼池快速排污;当进水口位置在水面以下30 cm时,除进水口附近及鱼池中心处速度稍快外,鱼池整体流场流线图与进水口位置在水下10 cm处并无显著区别,但进水口位置远离水面会使鱼池流场变动复杂,颗粒物的运动轨迹更为发散。
综上所述,水体循环量Q为1 200 L/h时,不同进水条件下,颗粒物运动轨迹和水流运动轨迹并不完全重合;进水流速的增加能够提高水体混合度,但并不会促进颗粒物的有效排出,反而会因离心力的增大产生相反的结果;在进水口位置在水面以下10 cm、进水流速1 m/s的水利条件下,鱼池内的水体流态无论从稳定性、排污性能还是节能方面都更符合实际使用需要。
3.2 PIV试验结果与对比分析
以水体循环量Q为1 200 L/h、进水口位置在水面以下10 cm、进水流速1 m/s水利条件的缩尺模型为例,进行PIV实测,使用总物质平均流速(Vmass average,即所有单位质量点的流速的平均值)作为流场描述的特征值。图7为不同水层位置CFD模拟速度与PIV结果的对比,从图中可以看出,CFD预测结果与试验数据吻合,误差基本保持在10%以内,CFD模拟图可以较好地反映了鱼池的实际流态。
以h=100 mm水层为例,CFD模拟结果显示,进水口附近(左下方)水流流速最快,对应流速约为35.9 cm/s,随着水流远离进水口,流速逐渐降低,在靠近进水口背面位置,达到30.5 cm/s左右。该趋势与PIV实测结果基本一致,分别为38.1 cm/s和34.2 cm/s。另外,模拟结果显示,沿着半径方向,水流流速从池壁至半径中心位置逐步递减,在半径中心处降至最低,而后逐渐升高,该现象也与PIV实测结果一致。但在以h=10 mm水层上,CFD模拟的总物质平均流速与PIV实测结果误差相对较大,尤其是进水口和鱼池中心处,最大误差可达21%,究其原因,是该水层靠近鱼池池壁及底部边界层,受边界层影响较大,在水流速度较大处影响更为显著。总体考虑,由于研究对象是流体流场,其受到的影响因素众多,现有的理论基础、技术条件和手段在这方面尚无法做到精准化模拟,本试验PIV实测与CFD模拟的总体趋势一致,产生的误差亦在可接受的范围内,因此,可以认为在流态描述上,CFD可以准确地模拟出了鱼池实际流态[30]。

a:h=140 mm,b:h=100 mm,c:h=80 mm,d:h=10 mm
4 结论
通过设置不同流量、不同进水速度和不同进水高度,分析了基于CFD模拟的圆形养殖池的径向速度分布以及基于PIV实测的鱼池实际流场。
(1)决定圆形鱼池流场的除鱼池几何参数外,还有进水流量、进水速度及进水高度,其中进水流量和速度是主要影响因素,这些因素决定了鱼池整体流场及流速分布。圆形鱼池可以通过拟合进水流量、进水口直径和进水高度来获得最佳流速和适宜的流场。
(2)在圆形鱼池直径2.0 m、水深0.8 m、水体量约为2.4 m3的几何尺度下,水体循环量Q为1 200 L/h时(循环量2 次/h),在进水口位置在水面以下10 cm、进水流速1 m/s的水利条件,鱼池内的水体流态无论从稳定性、排污性能还是节能方面都更符合实际使用需要。
(3)基于CFD技术的流场分析可以准确地反映圆形鱼池内部流场及速度分布,并能进一步地研究鱼池固液两相流,掌握颗粒物运动规律。采用CFD技术与PIV技术相结合的手段,可以得出不同鱼池形状及不同长深比、池底坡度等因素下的流场特性,既简化了试验手段,又具备实际工程意义,可为今后鱼池的结构建造与优化提供研究手段及理论依据。
□
