云爆式子母弹超声速分离气动特性研究

庞川博，蒋胜矩

(西安现代控制技术研究所，西安 710065)

0 引言

子母弹武器系统广泛运用于现代化战争中，通过调整母弹姿态，合理设计分离过程，实现子弹均匀散布，达到大面积毁伤的目的。当子弹采用云爆战斗部时，通过抛洒子弹可进一步扩大云团覆盖区域，从而提高二次起爆时云雾爆轰的打击面积和杀伤作用。不同于搭载常规战斗部的子母弹，为了达到预期的杀伤效果，云爆子弹外形通常为非旋成体以获得更大的装药量，为使云爆剂抛洒后与空气充分混合，子弹分离达到一定距离后需要开启减速伞进行减速，减速伞的释放与充气对分离后子弹的姿态和径向位移提出了更高要求，为保持姿态稳定，云爆子弹通常配备折叠弹翼作为安定面。考虑到在高速来流环境下子弹的出舱、弹翼张开、分离运动等过程具有显著的非定常特征，子弹运动过程中与母弹间流场结构复杂多变，激波干扰强烈，研究该过程中非定常流场变化以及采用不同分离条件下对子弹非定常气动特性的改变，对云爆式子母弹子弹气动外形设计、结构设计、分离方案设计等工作具有重要意义。

国外针对子母弹气动问题的研究起步较早，相关学者采用风洞试验或数值模拟的手段对子母弹分离过程激波相互作用、子弹气动特性变化、子弹绕流场分布以及子弹分离运动的位移和姿态变化展开研究。国内林靖明、雷娟棉、陶如意等采用定常流动数值模拟对子母弹不同位置典型姿态下的干扰流场进行了研究，随着结合动网格技术的流动/运动耦合求解方法的发展与完善，更多围绕多体分离非定常过程中流场演变/子弹动态气动特性的研究得到开展，其中王金龙等对多舱段、不同时序下子弹抛洒分离干扰特性进行了研究，得到了保证安全分离的时序间隔；袁武等通过研究子母弹绕流场非定常流动机理，建立了有效的干扰修正模型；靳晨晖等研究了分离过程中母弹运动时引起激波位置变化对子弹气动力的干扰，给出了锁定/放开母弹自由度时子弹运动轨迹；陈时通等采用嵌套网格模拟了母弹不同弹仓位置时对子弹抛撒后姿态的影响；张曼曼等模拟了多枚子弹在不同初始状态下的分离过程，研究了不同飞行速度、攻角下各个子弹间的流场干扰，但计算中并未考虑母弹影响。

上述研究工作普遍针对常见外形子母弹，对子弹分离后姿态、位移要求一般不严格，故模拟的分离过程时间均较短，旨在探索多体运动间流场变化以及短时间对子弹气动特性的干扰。目前对于分离过程耗时较长、分离后姿态、相对位移要求较高、外形通常为非旋成体的云爆式子弹的研究还较少，且很少考虑折叠安定面张开过程对分离的影响。文中通过耦合求解流体力学方程与动力学/运动学方程，结合动态嵌套网格技术，计算非旋成体子弹出舱、开翼、分离过程的气动特性与运动特性，讨论分离方式、分离时序、气动干扰等对后续分离运动的影响，为相应工程问题提供参考。

1 一体化数值模拟方法

1.1 流动控制方程

三维非定常可压缩N-S方程的积分形式表达式为：

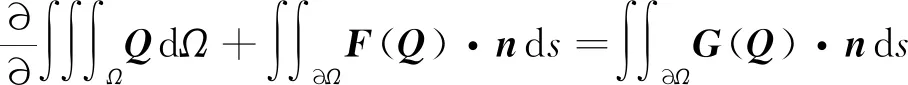
(1)

式中:为控制体；∂为单位控制体边界表面积；为积分面的单位法向矢量；为守恒形式的状态变量；()与()分别为对流项通量与粘性项通量。采用适用于非结构网格的二阶有限体积法求解流场，时间推进采用隐式双时间步方法，湍流模型采用Menter-SST两方程模型。

1.2 6DOF运动求解

运动过程中计算模型的姿态、位置的变化通过求解其动力学方程组与运动学方程组得到，在惯性系下，计算模型的平动与转动动力学方程组为：

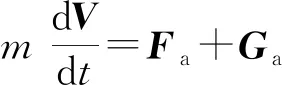
(2)

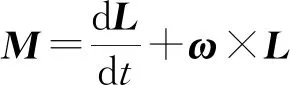
(3)

式中：为模型质心的速度矢量;与分别为作用在计算模型上的气动力与重力;为质量;为模型所受合力矩;为其惯性矩张量矩阵;为转动角速度。在已有当前时刻气动载荷的前提下，求解式(2)、式(3)得到当前的加速度与角加速度，再通过以下运动方程组求解得到计算模型的线位移与欧拉角如式(4)所示。

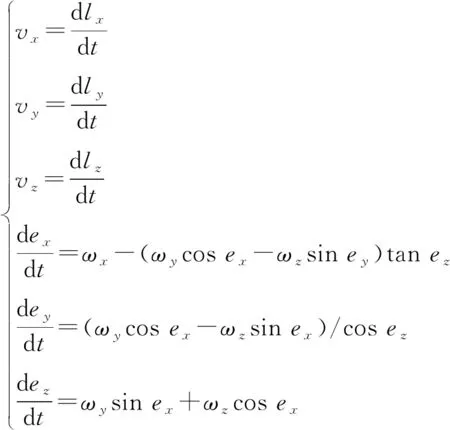
(4)

式中,(,,)、(,,)与(,,)分别表示模型的线位移、线速度与姿态角，姿态角满足--顺规。对于计算模型进行无控自由飞模拟时，随时间推进依次交替求解式(1)与式(2)、式(3)、式(4)即可得到当前时刻计算模型的气动载荷、绕流场分布以及运动状态。当描述弹翼张开过程时，需要依次单独求解部件的运动。

2 数值方法验证

通过模拟典型外挂物投放的运动过程来验证非定常流场计算模块与运动模块耦合求解的正确性。计算模型由机翼、挂架与外挂物组成，该外形多次用于嵌套网格与动态运动过程的验证，模型尺寸、来流条件参考文献[15]。采用非结构网格对计算域进行空间离散，在外挂物掉落途经区域加密背景体网格，在机翼、外挂物的前后缘同样进行加密，物面边界层网格以棱柱网格为主，底层高度为1×10m。计算网格分布如图1所示。

图1 机翼-外挂物计算嵌套网格

计算得到外挂物分离掉落后质心位置改变随时间变化的曲线如图2(a)所示，欧拉角曲线如图2(b)所示，线速度与角速度的随时间变化的曲线见图2(c)与图2(d)所示。对比计算结果与试验值可知，文中采用的耦合计算方法在求解物体运动过程中非定常流场时能够取得较好的效果。

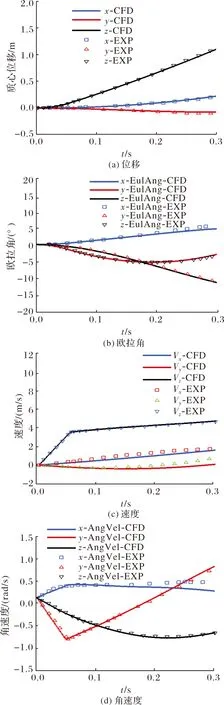
图2 CFD结果与试验结果对比

3 计算结果讨论

图3为云爆式子母弹计算模型，子弹背部外形近似为母弹二锥部分的1/4锥，弹体截面为扇形，质心位于距前端面60%处，装配于母弹内时子弹弹翼按沿弹轴周向折叠。为便于嵌套网格插值正常进行、避免初始时刻物面间的干涉，子弹、弹翼、母弹凹腔间均留有一定缝隙。

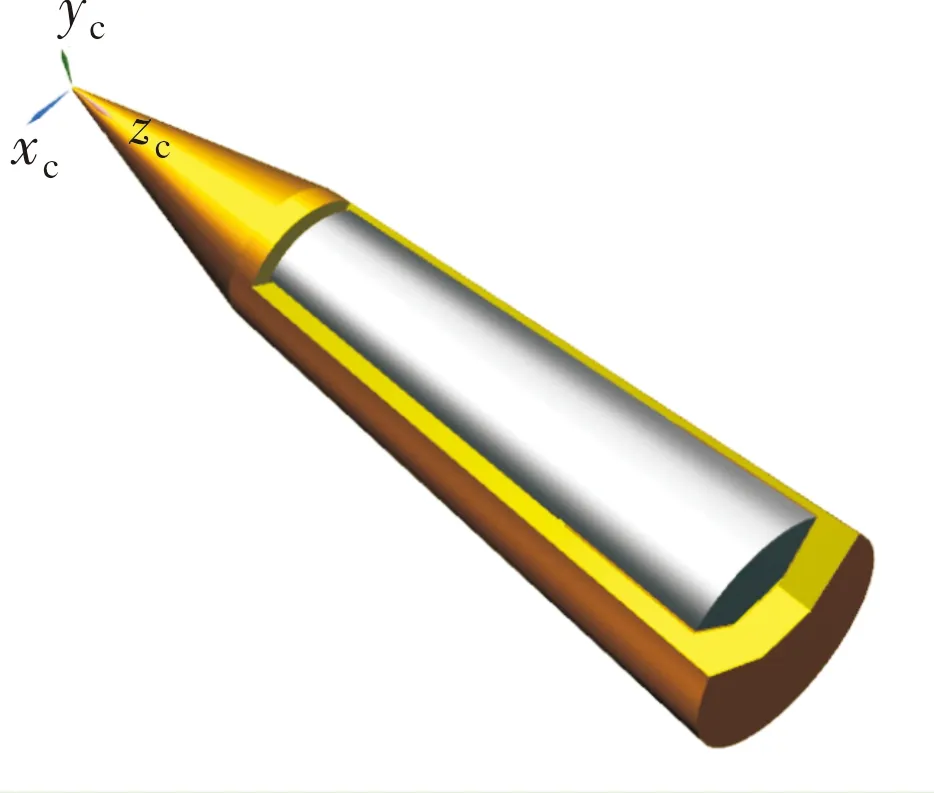
图3 云爆式子母弹计算模型

流场空间采用非结构嵌套网格进行离散，母弹，子弹、折叠弹翼各自独立生成计算网格，折叠弹翼处网格如图4所示，通过装配不同部件间网格，流场信息在部件网格重叠区域通过插值进行传递，部件之间出现相对运动时网格不进行变形，具有鲁棒性好、使用方便的优点。在母弹头部、弹腔内壁、子弹折叠翼、子弹分离运动区域进行网格加密以提高流场分辨率，网格向远场均匀过渡至较稀疏以降低计算量，网格数量约为900万。远场采用自由来流边界条件，母弹、子弹、弹翼均采用粘性无滑移壁面条件。

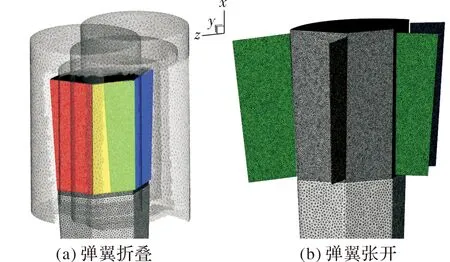
图4 弹翼处嵌套网格示意图

由于母弹的质量、惯量均远远大于子弹，在子弹分离运动过程中可忽略母弹位置、姿态的变化。初始时刻子弹折叠弹翼收拢并装于母弹凹槽中，子弹背部弧面不高于母弹二锥外包络，为降低计算量，本文仅考虑一枚子弹，着重讨论子弹与母弹间气动干扰以及不同分离条件影响。取来流2.0，6.98×10，温度288.15 K，来流攻角取0°，在该条件下进行流动定常求解，待流动发展均匀后作为非定常计算的初始流场。

数值计算主要考察不同分离条件下对分离过程、子弹运动过程的影响，分离条件可细分为：1)分离机构；2)子弹弹翼张开时刻；3)子弹弹出初速度。将不同分离条件组合成一系列工况见下表所示，计算不同分离工况时的分离过程，并评估上述分离条件对分离过程的影响。

表1 计算工况一览

上表中工况1与工况2主要考察初始弹出速度的影响。工况1与工况3主要考察弹翼张开时刻的影响。工况1与工况4主要考察分离形式的影响。采用弹簧作动式分离时子弹解除约束后按给定弹出速度开始运动，气囊式分离子弹解除约束并开始分离运动后，在气囊膨胀有效行程内子弹姿态保持不变。弹翼张开角速率统一为50 rad/s。

3.1 分离初期流场分析

以工况1为例，图5所示=0处流场截面可知，分离开始前，来流经过弹头产生的斜激波以及二锥扩张处膨胀波后作用于子弹背部弧面，由于子弹此时全部埋进母弹弹身，子弹头部大部分区域不受来流影响，母弹肩台缝隙处气流扩张产生明显的膨胀波，在缝隙内形成顺时针方向低能量回流区，且与外部流场几乎无质量交换。在子弹腹部与母弹凹腔缝隙处，靠近子弹头部位置为另一低速低压的回流区域，流动沿着缝隙下游方向压力逐渐增大，通过观察图6所示=0.1 m处流场截面，可知来流气流在母弹凹腔中间部位两侧进入缝隙内，当地流动速度与压强与外流场接近，气流继续向下游流经折叠尾翼处，由于缝隙进一步减小，气流流速降低，当地局部压力显著增大。在分离初始阶段，子弹腹部靠近头部部分表面压力较低，腹部靠后位置压力较大，放开自由度后受到低头方向力矩，子弹姿态呈低头方向变化，产生的法向力指向母弹，不利于分离过程进行，加之尾翼张开前子弹处于显著静不稳定状态，因此一定的分离初始速度是保证分离过程安全顺利进行所必须的条件。

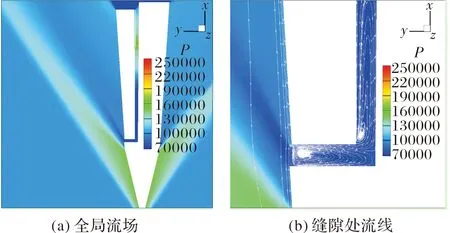
图5 分离初期z=0 m流场截面压力分布

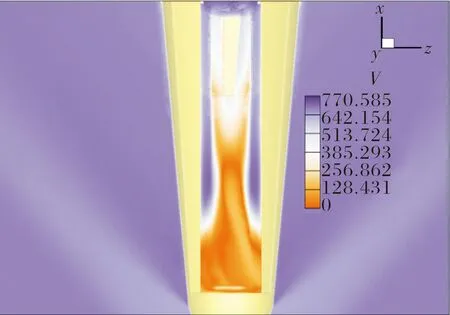
图6 分离初期y=0.1 m流场截面速度分布

给出分离开始后前20 ms时间段内在=0截面上的流场压力分布变化如图7所示，随着子弹头部逐渐暴露于母弹头部激波后的高压流场，气流受到子弹钝头部外形二次压缩产生强烈的弓形激波，沿子弹背部弧面方向，子弹激波与母弹头部激波方向一致；沿子弹腹部方向气流受膨胀作用加速进入母弹凹腔内，作用于凹腔底部前端形成局部高压区，并随子弹侧向运动继续进行而后移，此时在子弹腹部前端仍持续存在较大范围的低速低压回流区域，如图8所示。

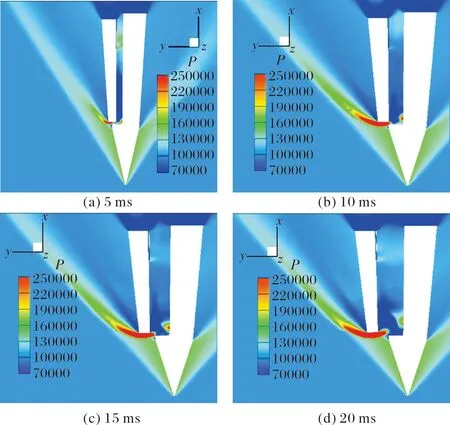
图7 z=0 m流场截面压力分布

图8 z=0 m截面速度矢量图

图9为前20 ms不同时刻在子弹腹部中心线处的压力分布，结合流场变化趋势，可以得出如下的压力变化规律：在零时刻，子弹腹部与母弹凹腔的缝隙前半部分受外流场影响较小，整个低压区压力梯度较小，缝隙后半部分外流场气流流入，局部压力显著增大，压力在折叠尾翼处达到峰值；子弹出现侧向位移后，气流从子弹头部缝隙处进入母弹凹腔内，凹腔内流动变化剧烈，气流膨胀产生显著低压区，同时由于凹腔空间变大，后部折叠弹翼处气流受挤压效果减弱，压力有所回落；随着两弹间距进一步增大，在外部流动持续进入腔内的影响下，凹腔前部低压区逐步减弱，凹腔后部折叠弹翼处受来流影响增大，局部压力有所回升。根据压力曲线变化可知，在尾翼张开前的分离过程，子弹始终受低头力矩影响。

图9 不同时刻子弹腹部中心线压力分布

3.2 子弹初始速度的影响

分离初期子弹受到显著的低头力矩，理论上更大的初始速度可以有效减短分离初期子弹头部低压区与尾部高压区的作用时间。计算工况1、工况2分别模拟了不同初速的分离过程，给出两种条件下子弹向速度与位置变化曲线，从图10中可知，两种工况在分离开始后子弹向侧推速度均开始衰减，工况1在=0.1 s附近向速度降至最小值，此时向位移已达到约1.15 m，在=0.13 s后向速度迅速增大，子弹运动远离母弹，分离过程正常进行；工况2由于初始侧推速度较低，在=0.07 s时向速度降至0 m/s，此时子弹向位移仅有0.5 m，随着向速度朝负向不断增大，子弹向接近母弹方向运动，分离未能顺利进行。

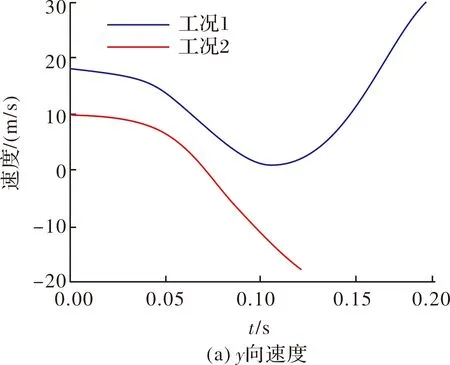
图10 不同初速下子弹沿分离方向速度与位移曲线

从运动过程可知，当前条件下，决定分离能否正常进行取决于向速度衰减至零时子弹在流场中的位置以及当前受力情况，图11给出两种工况下向力矩曲线与向姿态角曲线。可以看出在分离前期，子弹所受向气动俯仰力矩主要由母弹腔内流动影响，两种工况在前10 ms所受力矩曲线基本一致，力矩产生正的向姿态角，子弹向低头方向发生角位移，在来流作用下产生的法向力指向母弹，并使方向速度沿正向不断衰减。随着子弹不断远离母弹凹腔，向力矩逐步降低至零后朝负向增大，此时力矩使子弹产生抬头方向角速度，工况1达到的最大向姿态角约为7°，工况2最大向姿态角约为10°，子弹处于低头负攻角状态持续时间更长，如图12所示。此时子弹与母弹距离较近，尽管子弹已开始作抬头运动，但仍处于正向姿态角即负攻角，在向姿态尚未能够变化至抬头状态时子弹已和母弹发生碰撞，导致分离失败。

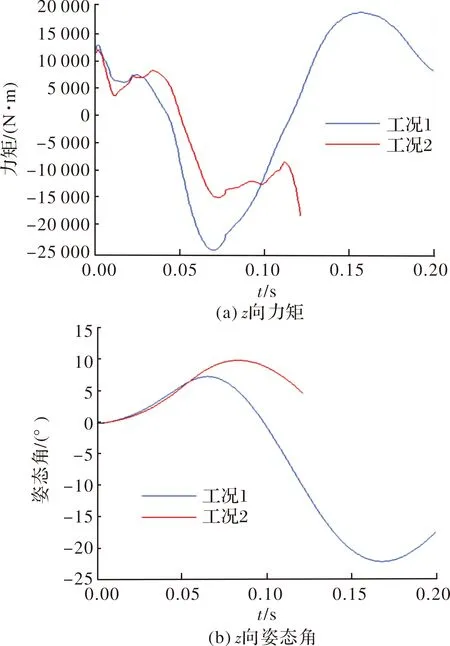
图11 不同初速下子弹z向力矩与姿态角变化曲线

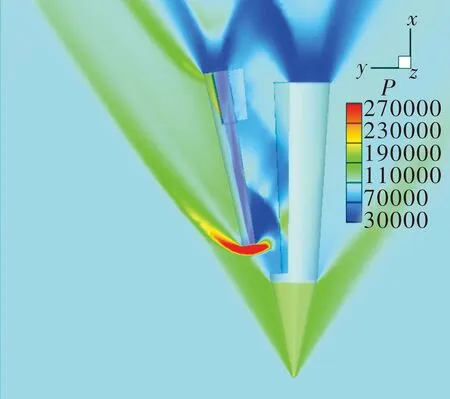
图12 t=0.07 s工况2压力分布

图13为工况1在=0.03 s时的流场压力云图，此时子弹的质心侧向位置与图12中工况2在=0.07 s基本一致，更大的初始侧推速度使得子弹受母弹凹腔作用的时间更短，导致同样位置子弹的负攻角更小，向侧推速度衰减更小；随着子弹逐渐远离母弹，母弹头部激波开始作用于子弹腹部前端，产生的力矩使得子弹持续作抬头运动，在相对来流正攻角条件下，子弹向速度增大远离母弹；随分离过程进一步进行后流场云图如图14、图15所示，随弹翼逐步张开到位，弹翼表面受力产生恢复力矩，当子弹具有的负向姿态角不断增大，其自身恢复力矩也不断增强，加之远离母弹后其头部激波强度减弱，子弹所受向力矩再次反向，子弹作低头运动且远离母弹，在俯仰振荡过程中直至向力矩达到平衡。

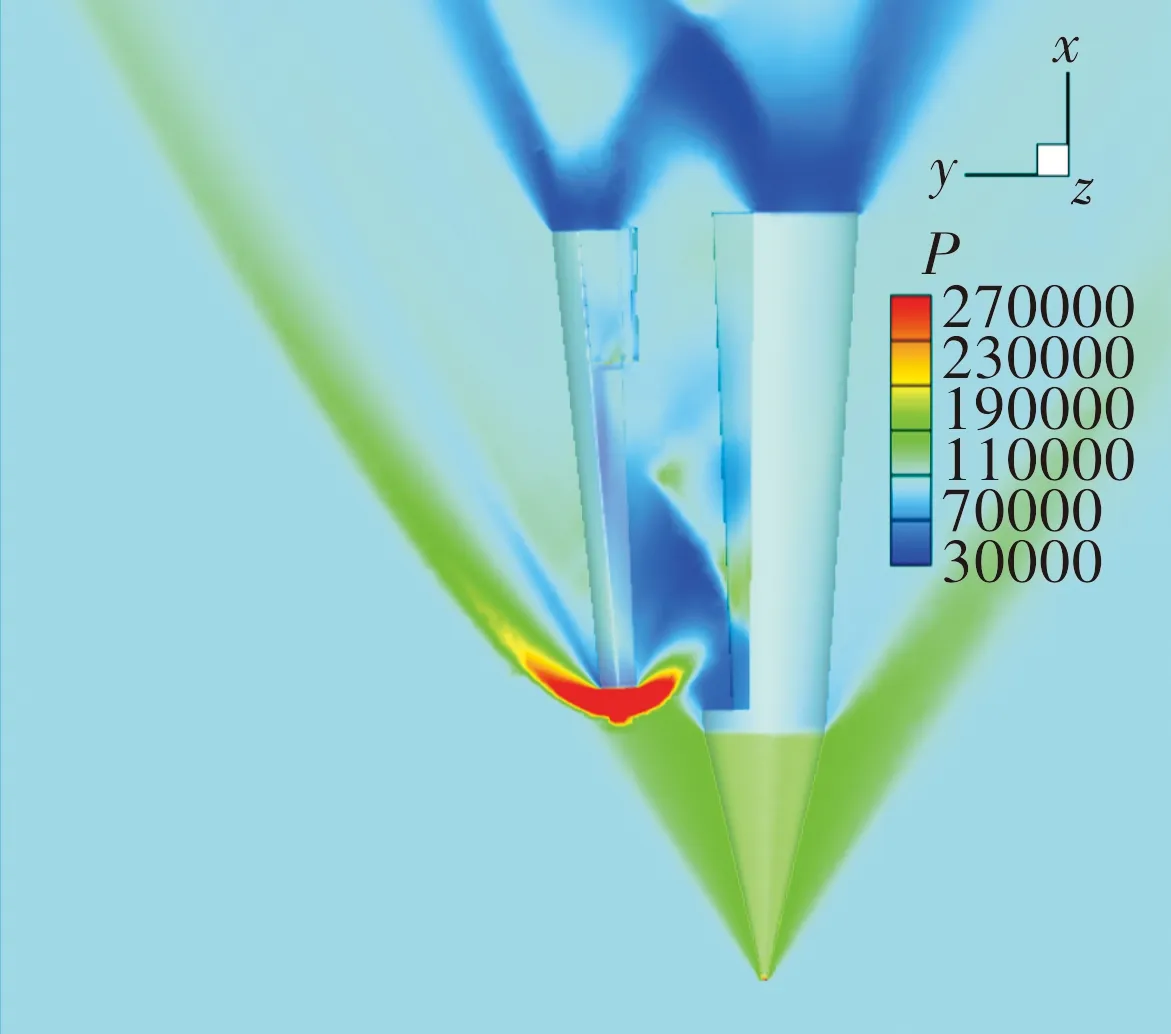
图13 t=0.03 s工况1压力分布

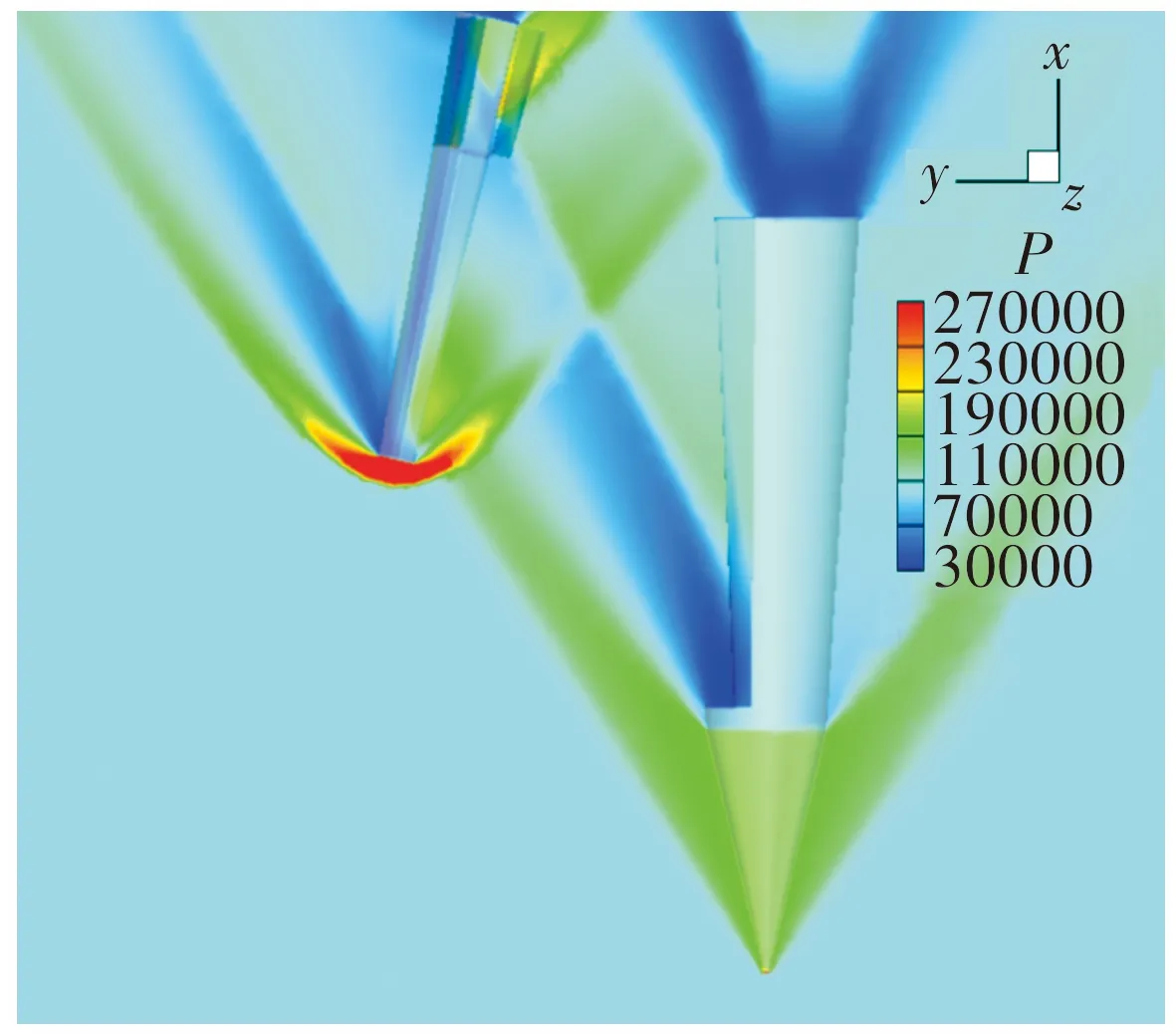
图14 t=0.13 s工况1压力分布

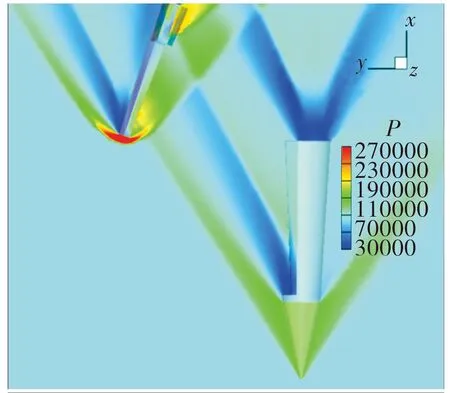
图15 t=0.18 s工况1压力分布

3.3 弹翼张开时刻影响

为保证分离过程中弹翼与母弹不能发生碰撞或干涉，通常在分离开始一段时间后弹翼才开始张开，工况1、工况3模拟了在相同分离形式、相同初始分离速度下不同弹翼张开时刻的分离过程，翼片从折叠到完全张开耗时约56 ms，工况1弹翼在取0.02～0.076 s完成张开过程，工况3弹翼在取0.04～0.096 s完成张开过程。图16分别给出子弹的向速度、位移以及向力矩、姿态角随时间的变化曲线。

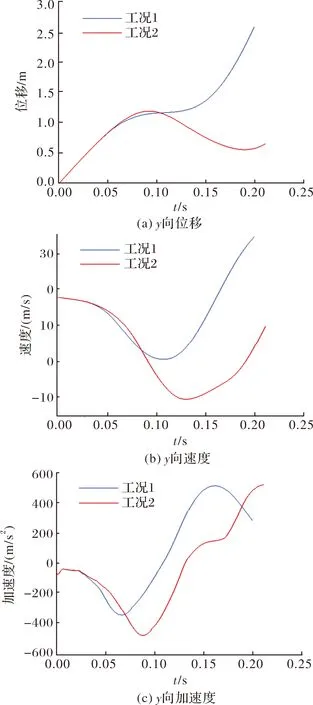
图16 不同弹翼张开时刻子弹侧向运动状态

如图16所示，前0.02 s两个工况子弹的运动状态基本一致，自=0.02 s时刻起工况1弹翼开始张开，由弹翼引起的额外向气动力增量使得向速度衰减加快如图16(c)所示，尽管在前0.1 s工况3的向位移略大于工况1，但更晚张开的弹翼使子弹前期俯仰稳定性更差，恢复力矩更晚与分离初期凹腔引起的低头力矩取得平衡，子弹最大低头姿态角，即图17所示向姿态角相比于工况1出现更晚且更大，达到约13°；由于工况3子弹长时间处于负攻角状态，使得其向速度衰减至零后反向增大，如图16(b)所示，子弹继续向靠近母弹方向运动，直至=0.13 s时刻姿态角恢复至零且朝负向增大，子弹相对来流具有正攻角，产生远离母弹的气动力使分离继续进行。

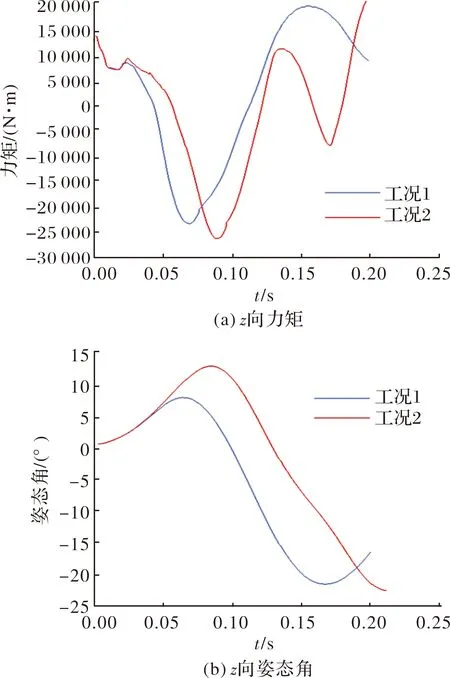
图17 不同弹翼张开时刻子弹z向力矩与姿态

图17(a)中=0.13 s至0.17 s时间段，子弹向姿态角负向增大，呈抬头趋势，其所受向力矩并未像工况1一样不断增大从而抑制姿态角变化，而是短时间内迅速反向变化加剧子弹抬头程度，这是由于子弹尾部及弹翼进入到母弹二锥后尾部膨胀波作用区导致，考虑到母弹弹长一般较长，文中计算中的二锥后尾部流场并不存在。在真实分离过程中，子弹距离母弹较近时，子弹头部激波经过母弹弹身反射后作用于其弹翼上，从而抑制子弹的抬头运动如图18所示，使得分离过程耗时更长，分离安全性更低。

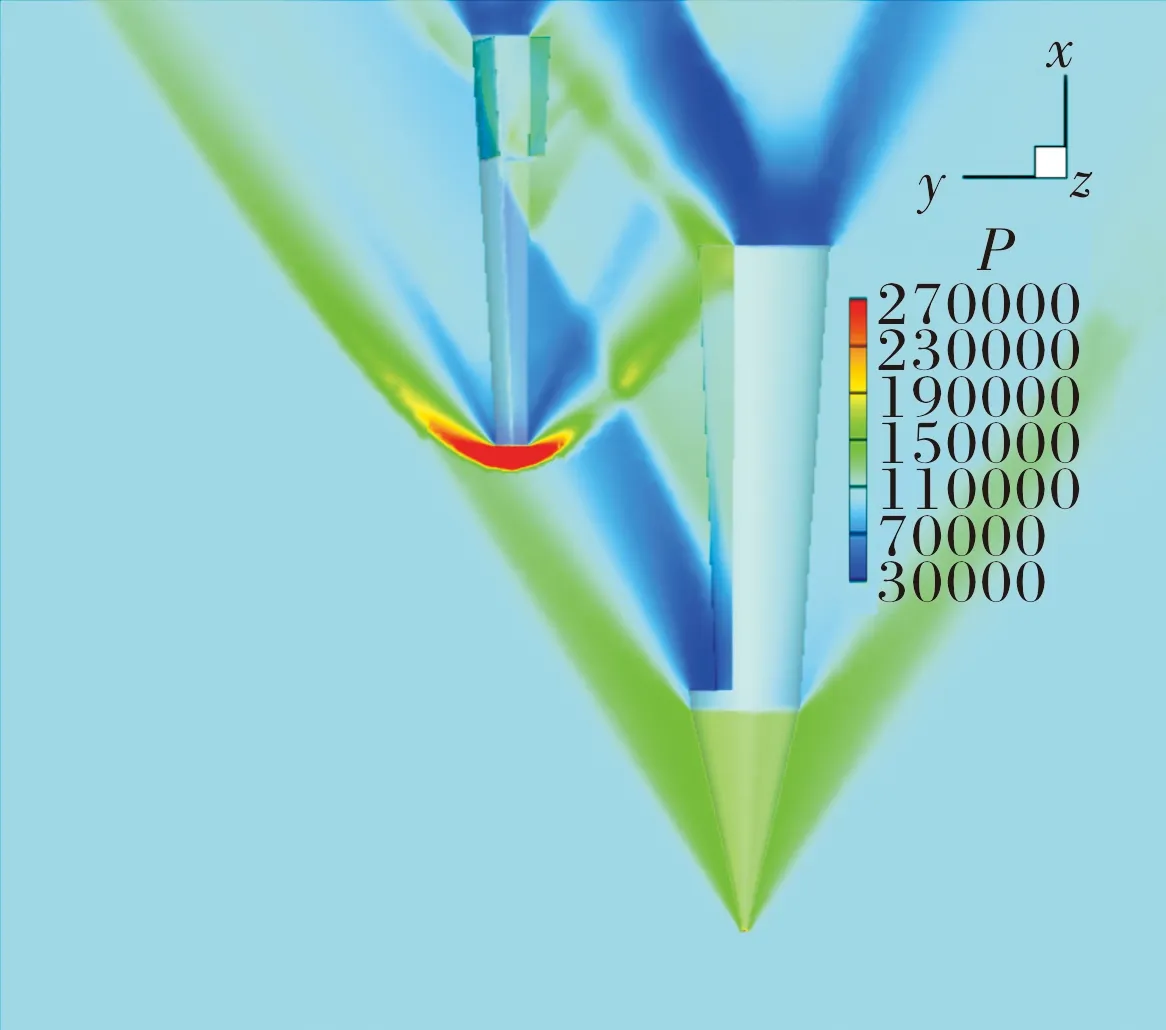
图18 子弹头部激波经反射作用于弹翼

3.4 气囊式分离的影响

不同于弹簧/作动器等机械力式分离机构，气囊具有更大的行程，分离过程冲击过载更小，在膨胀过程中通过与子弹腹部的大范围面接触来抑制其姿态变化，从达到稳定出舱姿态的目的。计算工况4气囊作用时间0.02 s，假设其匀速膨胀，总行程即为0.36 m，在该行程内子弹姿态保持不变且不因气动力矩而产生角加速度，给出工况4与工况1的向力矩曲线与向姿态角变化曲线如图19所示。

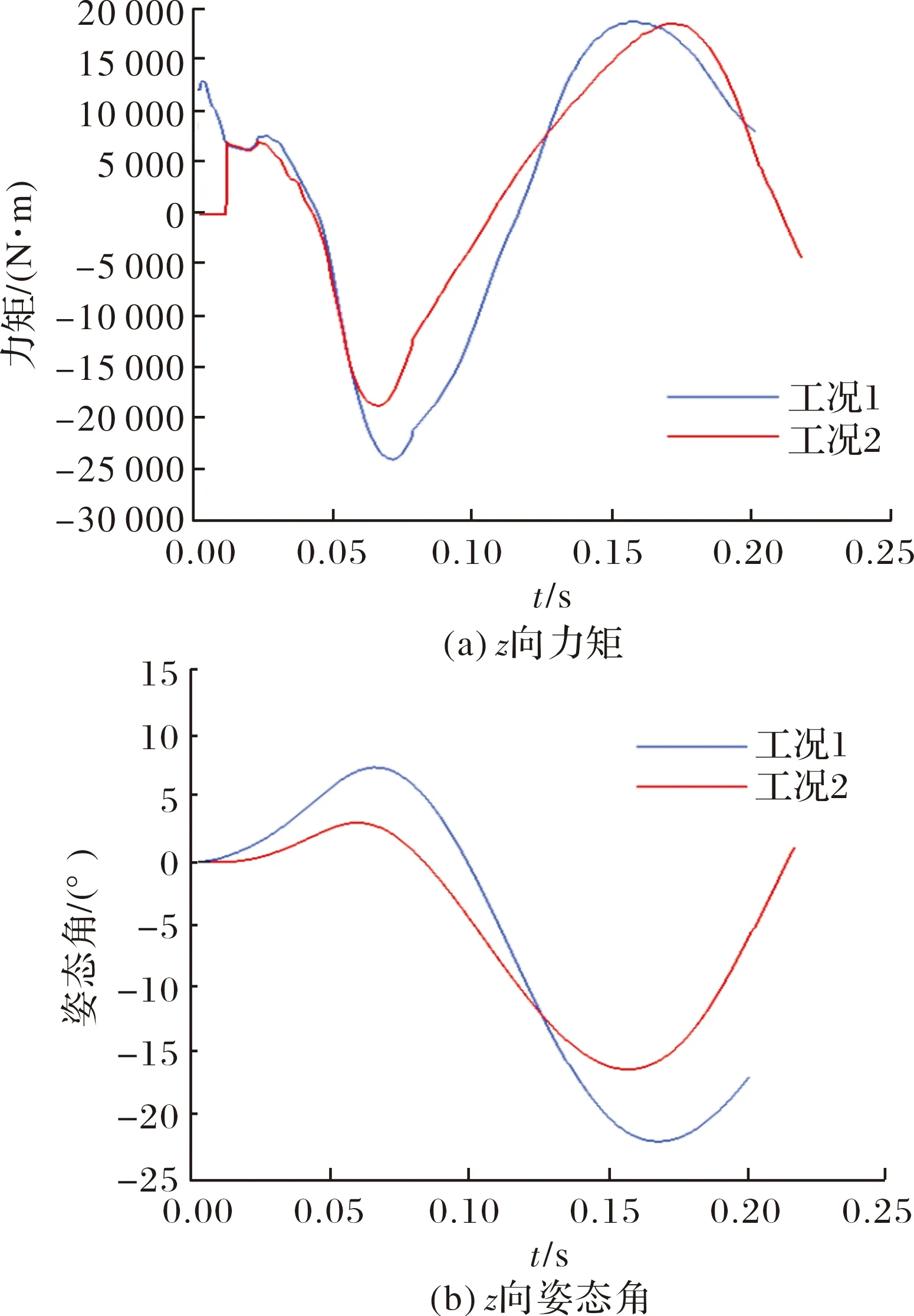
图19 不同作动形式下子弹z向力矩与姿态角

从图19中可知，前0.02 s工况4子弹在气囊作用下不受气动力矩影响，分离初期母弹凹腔对其引起的低头力矩效果显著减小，子弹最大低头姿态角约3°左右，达到所有工况分离初期姿态变化最小，随后子弹在恢复力矩以及母弹头部激波共同作用下开始抬头方向运动，迅速远离母弹。观察其向速度与位移曲线如图20所示，由于分离前期处于负攻角的时间更短，工况4的向速度衰减最小，前0.2 s子弹侧向位移更大，后续分离过程由于工况4的正攻角振荡幅值更小，其后续向最大速度会保持在31 m/s以内，长时间内侧向位移较工况1更小。

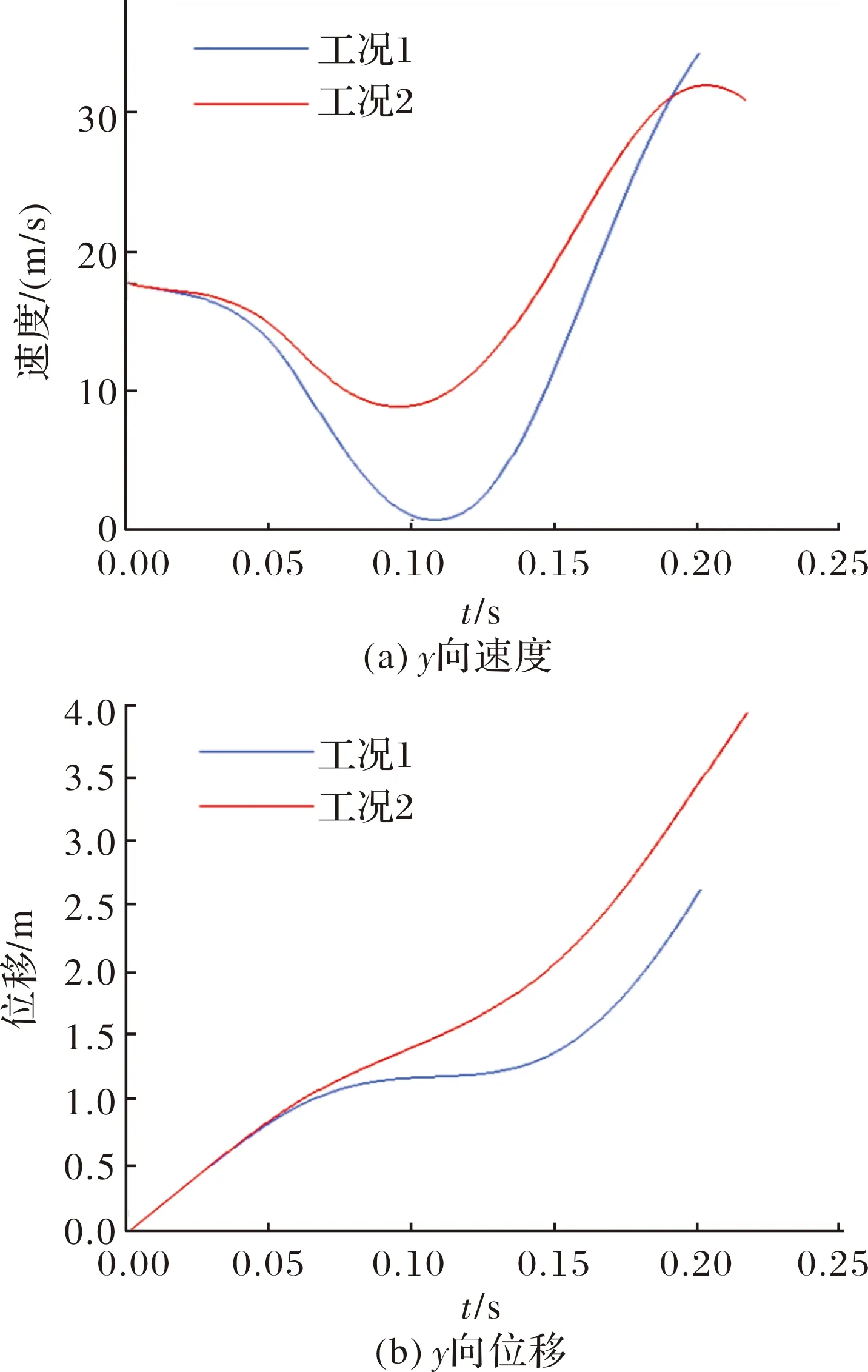
图20 不同作动形式下子弹y向速度与位移

4 结论

采用动态嵌套网格，通过耦合求解流动控制方程与动力学方程，对云爆式子母弹分离过程进行了数值模拟，重点关注初始分离速度、弹翼张开时刻以及不同分离机构对分离过程的影响，通过对子弹气动载荷、运动姿态、流场分布进行分析，得出以下结论：

1)分离初期，母弹凹腔前部为低压回流区，外部流动从凹腔中部两侧进入到缝隙内，在腔体后部折叠尾翼处受到挤压形成高压区，子弹在凹腔内流作用下受到低头方向力矩，此时子弹弹翼未张开，处于强静不稳定状态，低头姿态下产生的气动力对分离过程起阻碍作用，随着子弹与母弹的间距变大，凹腔的影响逐步减弱。

2)保证子弹能够顺利离开母弹凹腔影响需要足够的初始分离速度，初始分离速度越大，分离前期受母弹凹腔内流影响的时间越短，子弹前期的低头姿态角越小，分离安全性越高。当初始分离速度不够时，尽管子弹自身稳定度尚能够调整姿态，但前期过长的时间处于负攻角状态所引起的侧向分离速度过度衰减下，分离过程无法继续进行。为提高安全性，在满足分离机构体积、弹体过载等要求时，应尽量提高初始分离速度。

3)子弹弹翼张开后会增大横向方向阻力，导致分离速度降低，但全弹稳定性会显著增大，在分离前期受凹腔影响低头过程或是分离后期受激波影响抬头过程中，均可产生更大的恢复力矩，降低子弹角位移振荡幅值。当弹翼张开时刻较晚时，分离前期子弹低头姿态角更大，处于负攻角时间更长，分离方向速度与位移均更小，分离过程耗时更长，分离安全性更低。故在满足弹翼与母弹间不发生碰撞前提下，尾翼应尽早张开。

4)采用气囊进行分离时，膨胀后气囊的体积以及与子弹腹部平面的大面积解除可以有效抑制分离初期母弹凹腔对子弹姿态的影响，后续弹体运动过程中俯仰振幅更小，侧向速度变化量更小，子弹的速度、位移更加可控。