某战术导弹舵面异常高频抖动机理分析
2022-06-06刘钧圣刘万刚张延风叶正寅
刘钧圣,刘万刚,张延风,叶正寅,叶 坤
(1 西安现代控制技术研究所,西安 710065;2 西北工业大学航空学院,西安 710072)
0 引言
舵翼是控制导弹姿态的关键气动部件,舵翼的异常振动无疑会给导弹的正常飞行以及任务完成质量产生重要的影响。
造成舵翼振动有多种诱因,空转和初始条件对导弹舵翼的非线性振动有重要的影响,空转间隙的增加会导致气弹响应的频率下降;伺服系统也可以导致导弹的气弹性能恶化。从工程应用角度出发,杨立海等分析了由于速率陀螺组供电断路器故障导致的抖动现象;李辉分析了由于滤波电容性能不合格,使得角速度模拟量零位噪声过大,导致电动舵机抖动;李家旭分析了由于襟翼带应力安装和间隙控制不当引起异常抖动;马位涛分析了由于飞行员不当操纵方向舵导致的异常抖动;付长安等从液压阻力器稳定性方面分析了水平尾翼抖动故障;杨璐等对某型炸弹制导化改造舵面及其操作系统进行颤振分析;王强等采用基于模态综合法分析了含间隙折叠舵面的极限环振动;李治涛等采用CFD/CSD耦合数值和试验方法分析了双线性非线性全动舵面的极限环振动;隋鑫等分析了含间隙舵面非线性颤振特性;何昊南等进行了有间隙折叠舵面的振动试验与非线性建模研究。Kim等探讨了复合材料的铺层对舵翼振动的影响;Yoo和Aksoy等采用了不同的方法旨在抑制舵翼的振动。
对于亚声速导弹而言,导致舵翼振动还可能是因为底部分离流对舵翼的诱导作用,文中根据某导弹外形和实际测量获得的振动现象,探讨了底部分离流对舵翼的诱导振动问题,揭示了该外形下舵翼振动的诱发机理,为抑制此类诱发振动问题指出了方向。
1 计算方法
三维非定常N-S方程在直角坐标系中的积分守恒形式为:
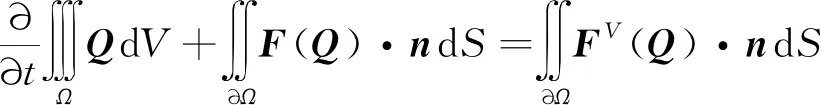
(1)
式中:为控制体;∂为控制体单元边界;为控制体体积;为控制体面积;为时间;为守恒变量,=[,,,,];()为无粘通量;()为黏性通量;为面积d外法线方向;,分别为密度、单位控制体∂的总能;,,分别为,,方向的速度分量。
采用SST-两方程湍流模型对流场进行模拟,采用有限体积方法进行空间离散,空间格式采用AUSM,时间推进采用LU-SGS。非定常计算中采用双时间推进方法。
2 验证算例
采用CRM机翼跨声速抖振算例验证采用的URANS求解器的可靠性。CRM模型是AIAA第4次阻力预测会议中采用的标模,机翼模型半展长为634.6 mm,参考弦长为151.3 mm。如图1所示,采用非结构混合网格开展数值模拟,网格单元总数约为500万,远场约为参考长度的50倍。壁面第1层网格高度为参考弦长的2×10,附面层网格约为40层。
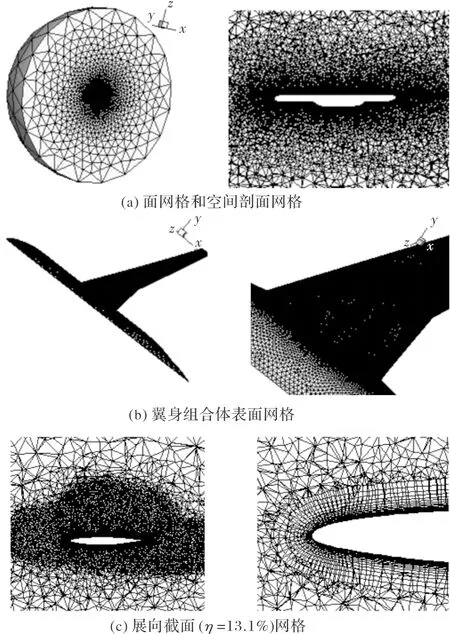
图1 CFD计算网格
首先对来流条件为:0.847,迎角为2.47°的定长状态开展计算。基于参考弦长2.2×10,分别基于S-A模型和SST模型开展计算,图2为机翼上下表面不同位置处压力系数分布,其中为截面位置相对于展长的百分比,可以看出两种湍流模型的计算结果均与试验数据吻合较好。
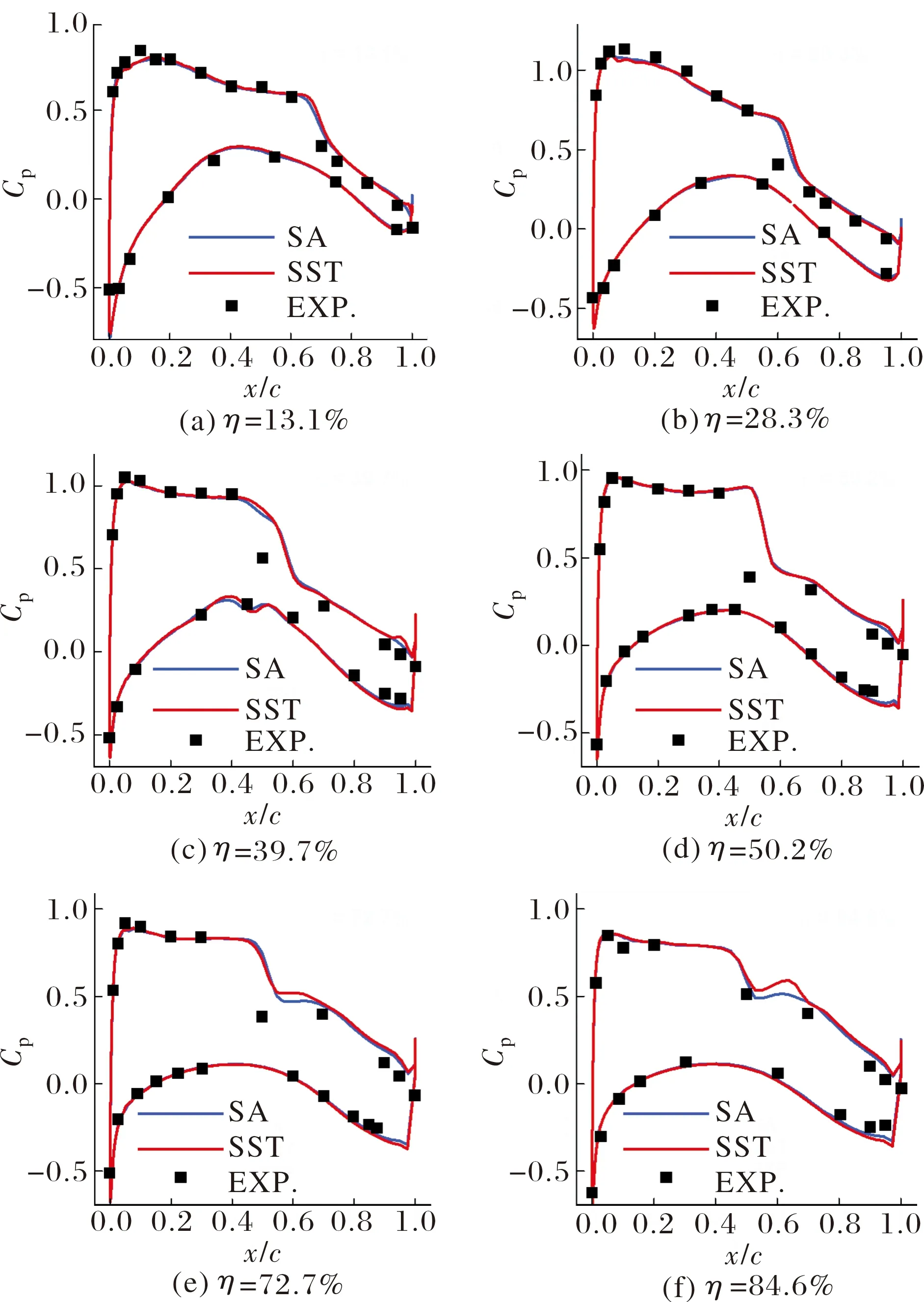
图2 机翼各展向截面压力系数与试验结果比较
进一步采用URANS求解器对来流条件为0.85,=4.9°,2.2×10的非定常状态开展计算。计算中采用SST湍流模型,时间步长为 2×10s。图3为非定常脉动压力均方根的分布,可以看出计算结果和风洞试验结果相似。同时选取6个典型的监测点~,监测其压力脉动,图4为监测点上压力脉动响应及其功率谱分析,可以看出点压力脉动很小,并且没有明显的主频特性。点和点位于激波振荡的区域,压力系数波动幅值达到了0.7以上,主频约为60 Hz左右。点压力系数波动幅值明显小于激波振荡区,但仍然具有较好的周期性特征,主频约为60 Hz,与激动振荡频率一致,失稳频率=0.03。位于激波振荡区域,位于激波后分离区域,可以看出这两个监测点的压力脉动幅值均小于激波主振荡区域。同时频率分析结果可以看出除了60 Hz的低频响应外,还存在明显的高频振荡,高频频率约为400 Hz。高频振荡是由K-H型流动失稳造成的,并且其失稳频率约为0.21,与文献[19]中试验结果比较吻合。上述计算结果表明,URANS数值模拟方法可以比较准确地预测三维非定常流动现象。
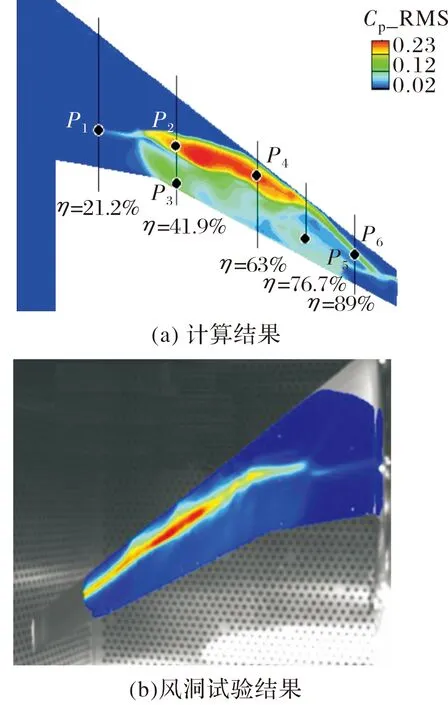
图3 机翼上压力脉动均方根与风洞试验结果的对比
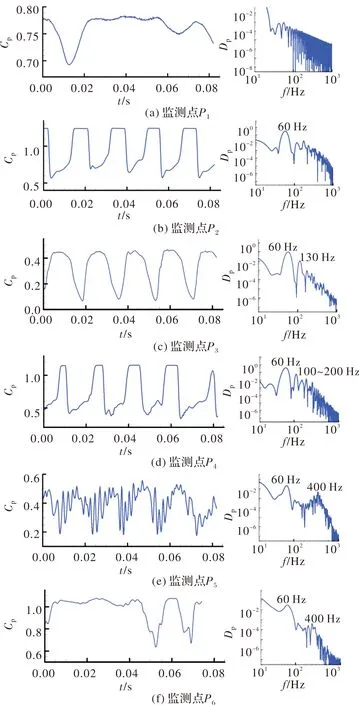
图4 监测点的压力系数响应及其功率谱分析
3 结果与分析
3.1 分析模型和计算状态
为了从气动的角度研究亚声速导弹舵的振动问题,首先将某导弹外形进行简化,去掉了弹体的头部,提取了舵面、弹体以及底部3个主要部分。由于舵面的气动干扰主要来源于这几个部分。为了找出诱导舵面非定常载荷的主要部件,主要对模型1—单独舵面翼模型;模型2—弹身、底部和舵面(简称原始模型);模型3—弹身、弹身延长和舵面(弹身延长是为了消除底部的影响,从而与模型2可以形成对比,简称弹身延长模型)这3种模型进行数值模拟后分析各部部件对舵面非定常载荷的影响,如图5所示。
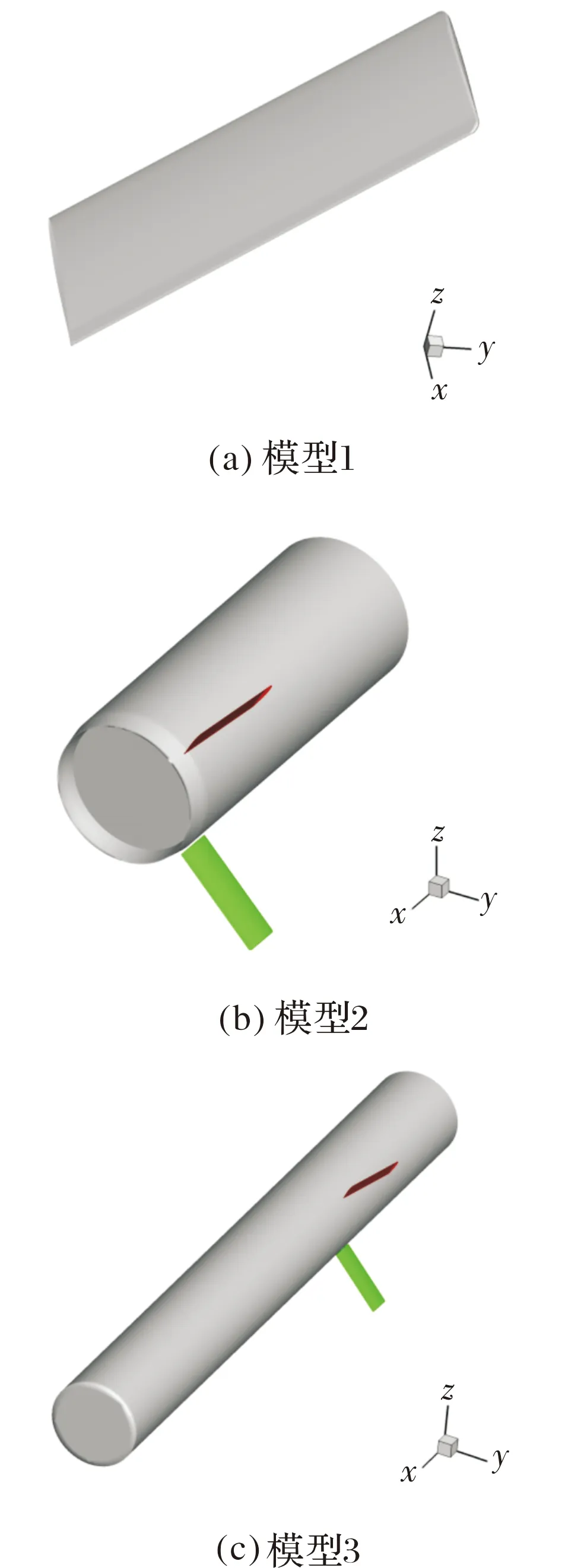
图5 3种计算模型
通过模型1与模型2之间形成对比可以分析出弹身和底部的影响;通过模型2与模型3之间形成对比可以分析出底部的影响。 状态下,来流状态为:飞行高度260 m,0.76,1.77×10,迎角为3°,舵偏角为5°。
为了对舵面和弹体尾部的分离区进行准确的数值模拟,网格生成中对舵面的上表面和弹体尾部的空间网格进行加密。同时为了在不影响问题分析的条件下降低计算量,舵面只取半模,弹身和底部取全模。网格单元总数约为550万,第一层附面层厚度为1×10m,附面层中生成30层网格,附面层网格增长率为1.3。图6为数值模拟中采用的网格。
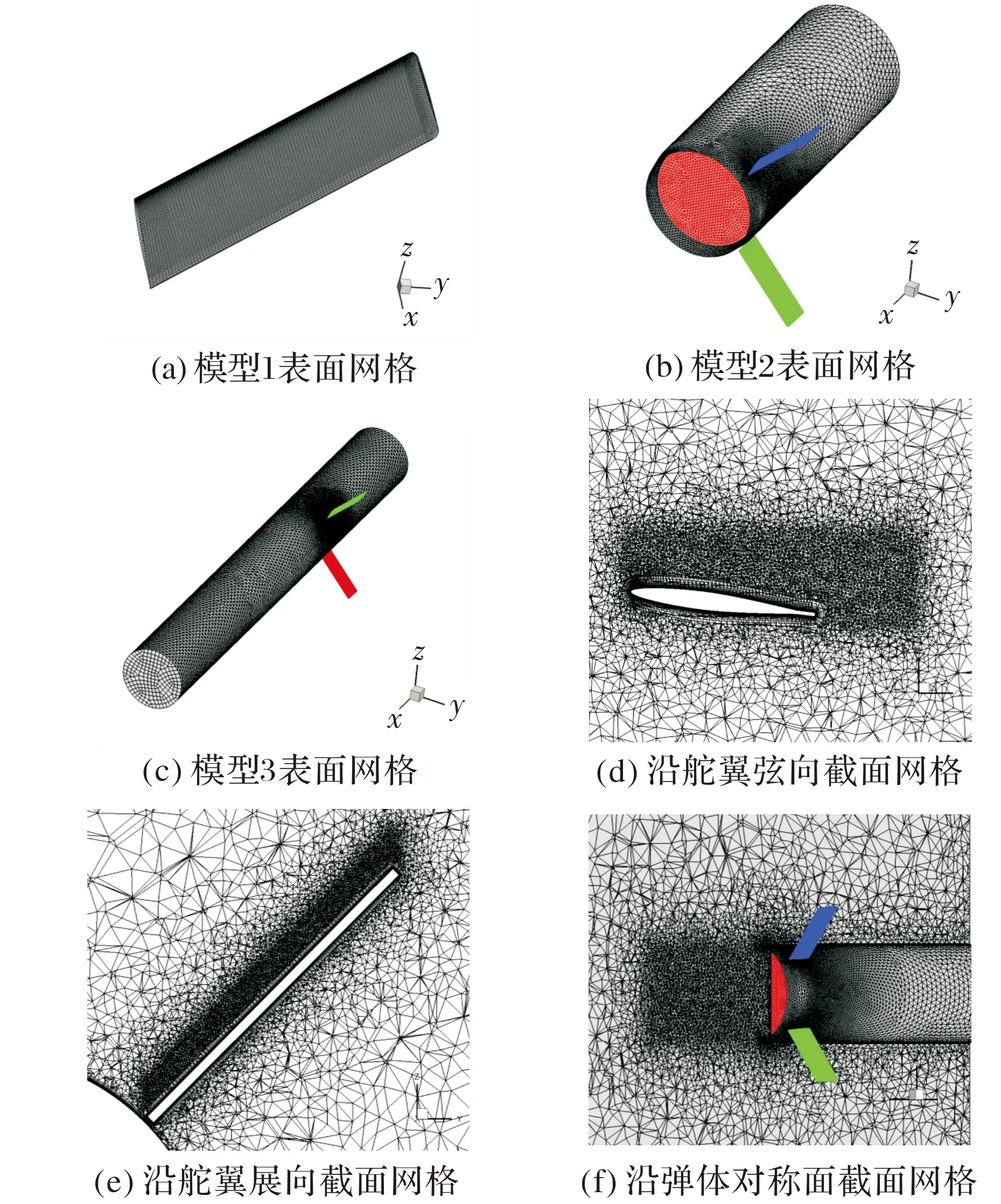
图6 计算网格
3.2 气动力非定常特性的分析
图7为单独舵面模型下舵面3个方向的非定常气动力随时间的变化。可以看出,由于方向为舵面的展向方向,舵面方向非定常气动力的绝对值和脉动幅值都比较小,因此对和方向的非定常气动力进行分析。
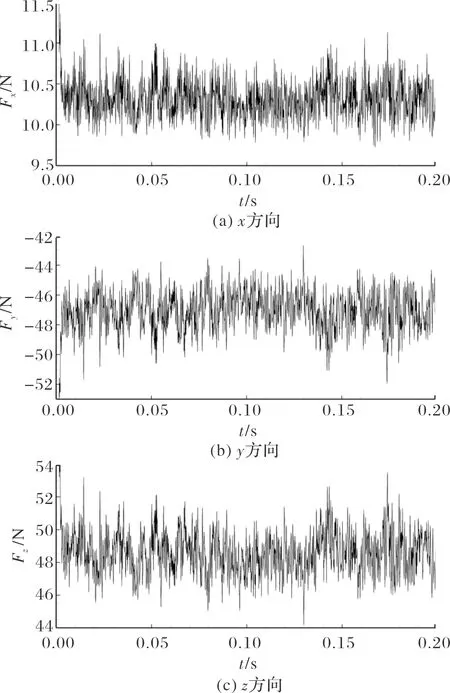
图7 单独舵面非定常气动力随时间的变化
图8为和方向的非定常气动力的频谱分析,可以看出对于单独舵面模型,舵面上非定常气动力的脉动主频在为10 Hz附近,同时也存在一些高频脉动,频率在33 Hz和56 Hz附近,主频的幅值约为6.0,幅值相对较小。
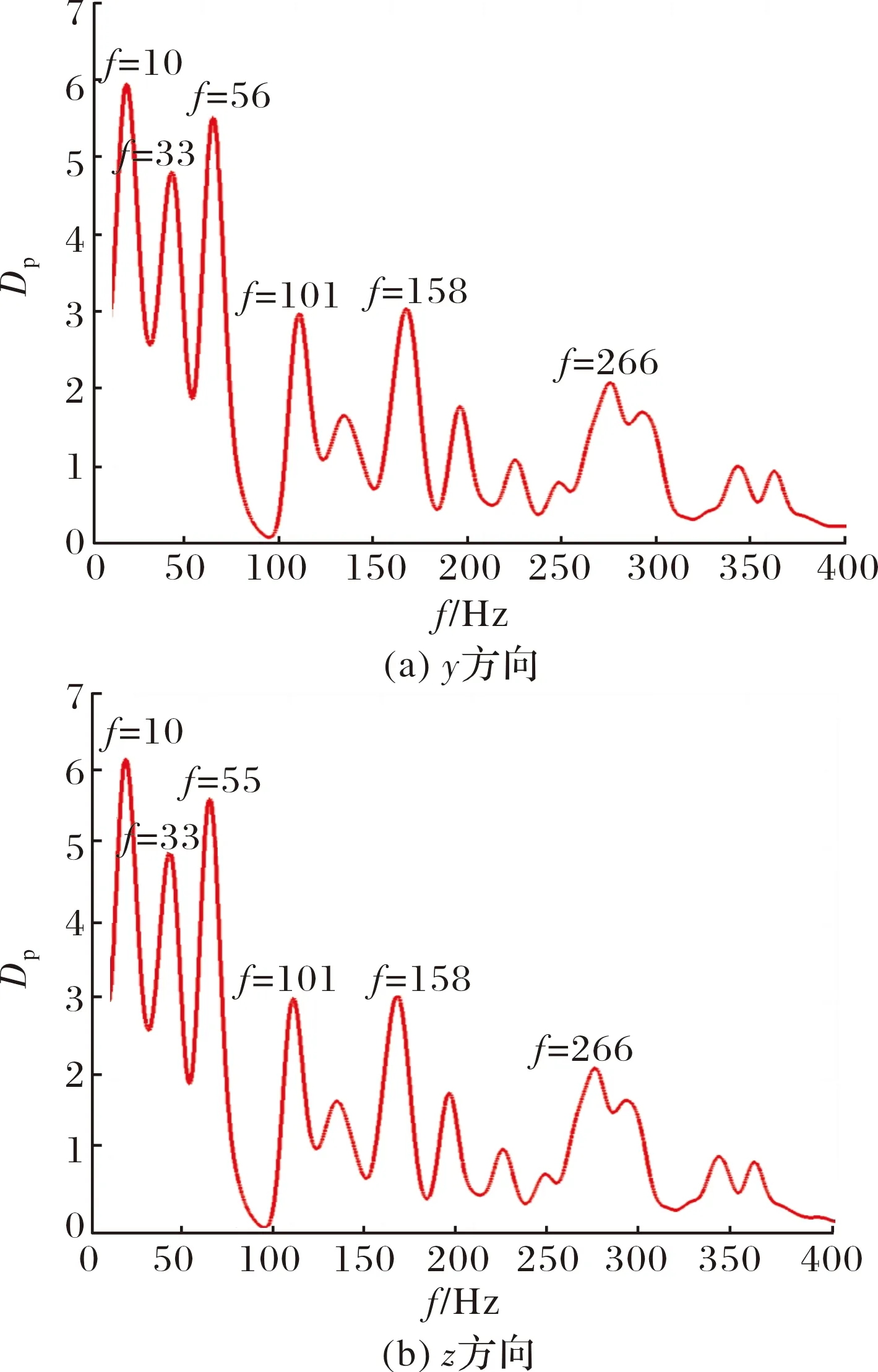
图8 单独舵面模型非定常气动力频谱分析
图9所示为原始模型下舵面和方向的非定常气动力随时间的变化。可以看出由于原始模型中,舵面附近存在弹身和弹体底部。因此,相对于单独舵面模型,原始模型考虑的弹身和弹体底部的影响。
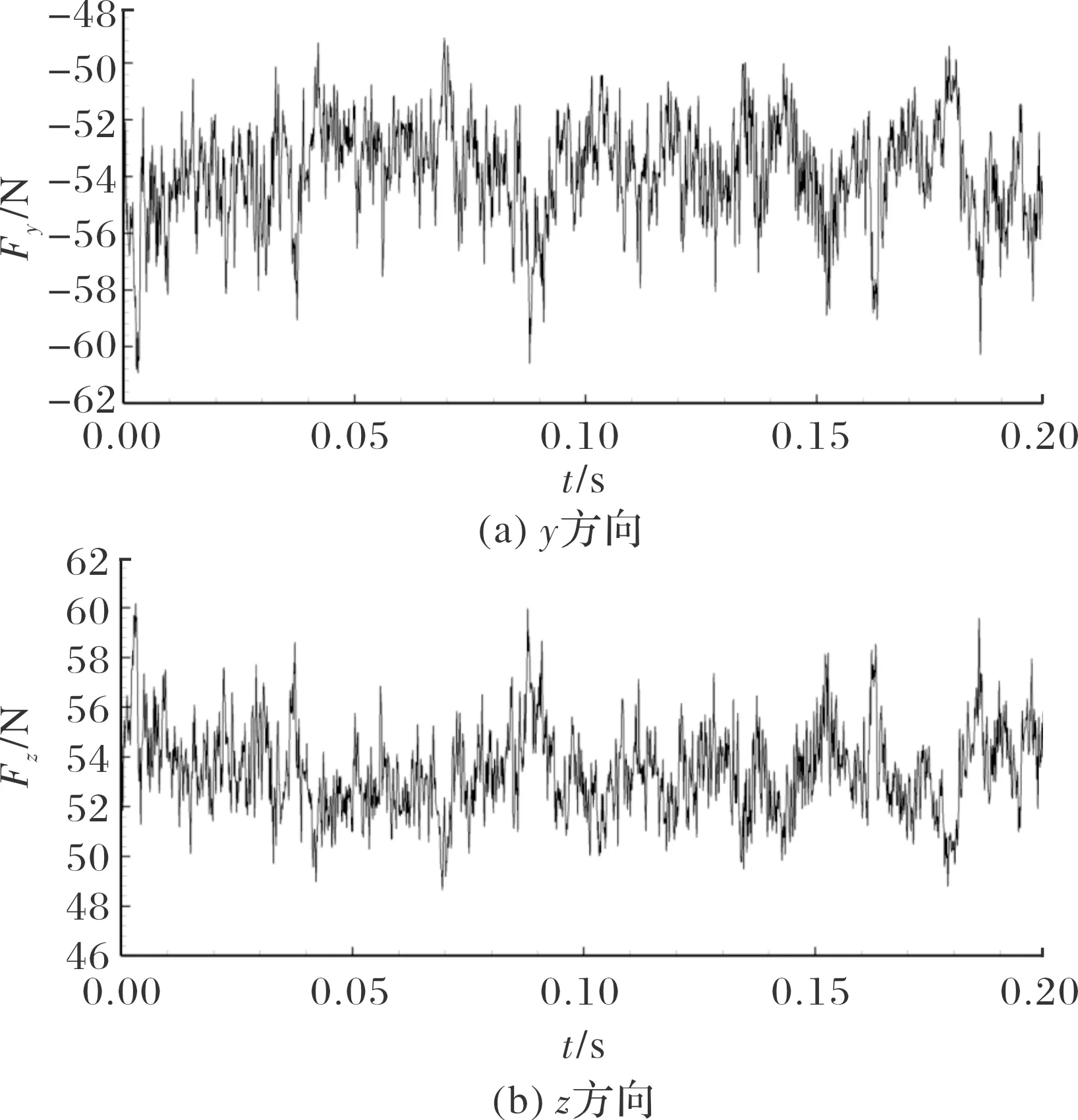
图9 原始模型非定常气动力随时间的变化
图10为和方向的非定常气动力的频谱分析。可以看出,对于原始模型,舵面上非定常气动力的脉动主频在在28 Hz和30 Hz附近,同时也存在一些高频脉动,频率在85 Hz附近;主频的幅值约为33.0,幅值相对较大。
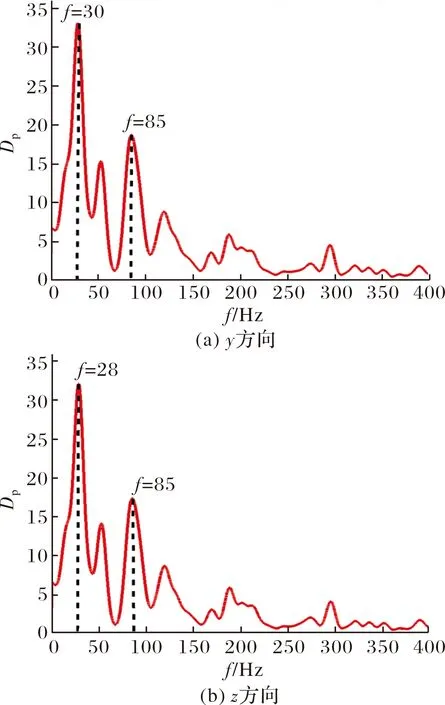
图10 原始模型非定常气动力频谱分析
因此,相对于单独舵面模型,在弹身和弹体底部的综合影响下,舵面上非定常气动力脉动的幅值大幅增加的同时主频率也会增加。频谱分析的幅值由6.0增加到33.0,主频率由10 Hz增加到30 Hz。然而上述的结果并不能分析出是弹身的影响占主导,还是弹体底部的影响占主导。
图11为弹身延长模型舵面和方向的非定常气动力随时间的变化。由于弹身延长模型中,舵面附近主要存在弹身,由于弹身延长弹体底部距离舵面较远。因此,相对于单独舵面模型,弹身延长模型仅考虑弹身影响。图12为和方向的非定常气动力的频谱分析。
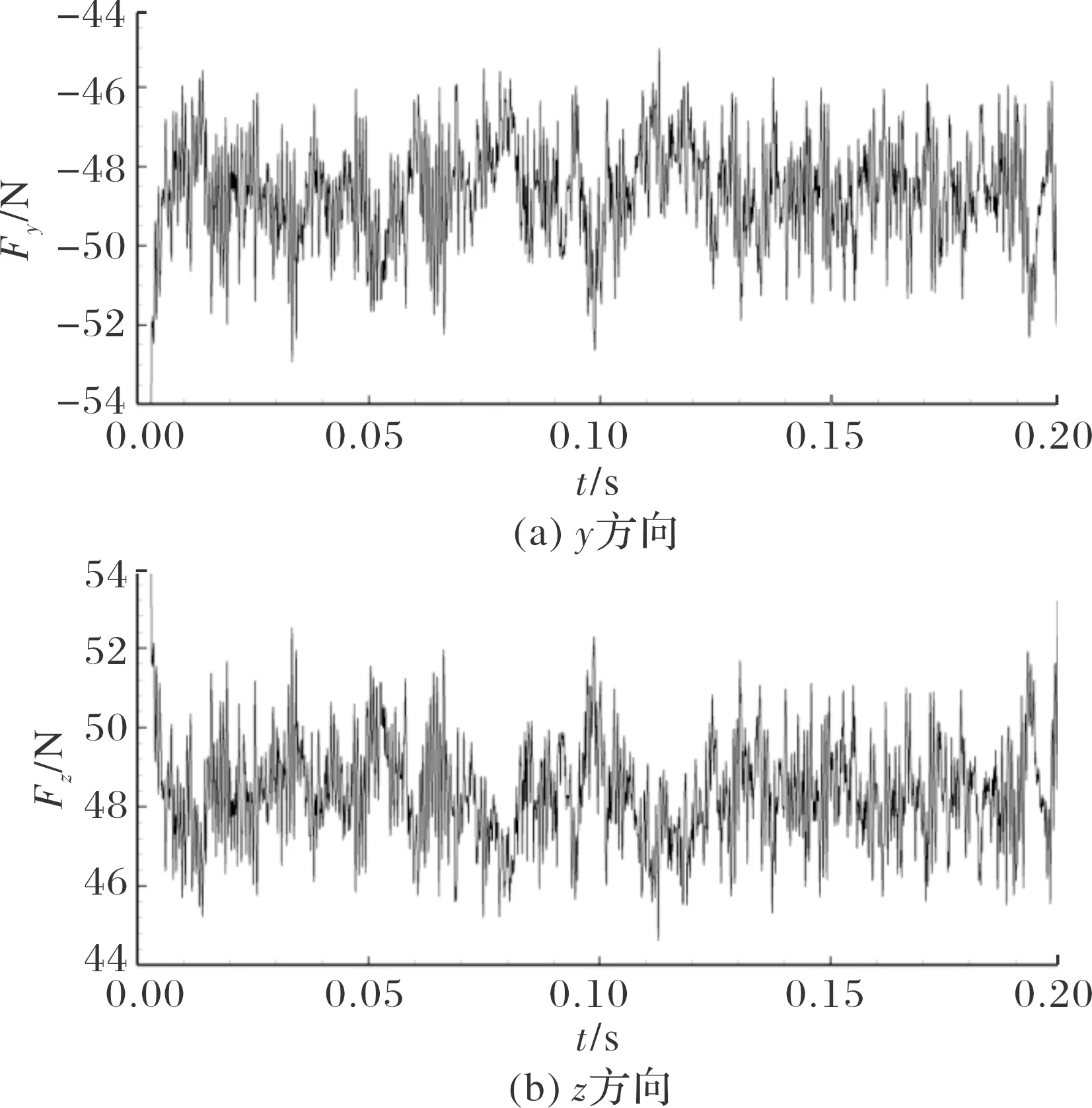
图11 弹身延长模型非定常气动力随时间的变化
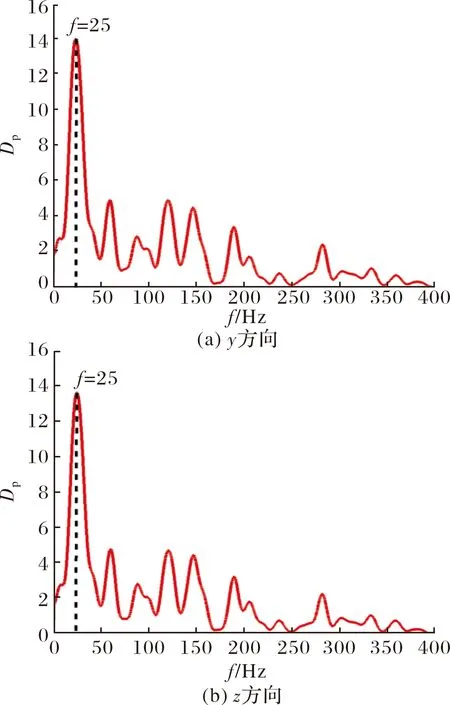
图12 弹身延长模型非定常气动力频谱分析
可以看出对于弹身延长模型,舵面上非定常气动力的脉动主频在在25 Hz附近,主频的幅值约为14.0,幅值相对较大。
和单独模型结果相比,弹身延长模型中舵面上非定常气动力脉动的幅值大幅增加了,同时主频率也增加了。频谱分析的幅值由6.0增加到14.0,主频率由10 Hz增加到25 Hz。这说明考虑弹身的影响后舵面上非定常气动力脉动的幅值大幅增加的同时主频率也增加了。
和原始模型相比,弹身延长模型中舵面上非定常气动力脉动的幅值减小的同时主频率也降低了。频谱分析的幅值由33.0降低到14.0,主频率由30 Hz降低到25 Hz。说明当同时考虑弹身和底部的影响后,舵面上非定常气动力脉动的幅值会大幅增加的同时主频率也增加了,说明底部非定常流动会诱发舵面产生更大的非定常脉动载荷。
导弹模型如图13所示,在实际飞行中研究人员中发现当发动机工作时,舵面抖动幅度较小。然而,当发动机工作结束时,舵面存在明显地大幅高频抖动,抖动频率在30 Hz附近。结合分析结果可知,弹身延长模型仅仅考虑弹身的干扰,相当于发动机工作状态,舵面非定常气动力脉动并不是很大。然而当进一步考虑底部的影响时,相当于发动机关闭状态,弹体底部非定常分离流动较强,舵面非定常气动力脉动大幅增加,同时脉动频率也是在30 Hz附近。
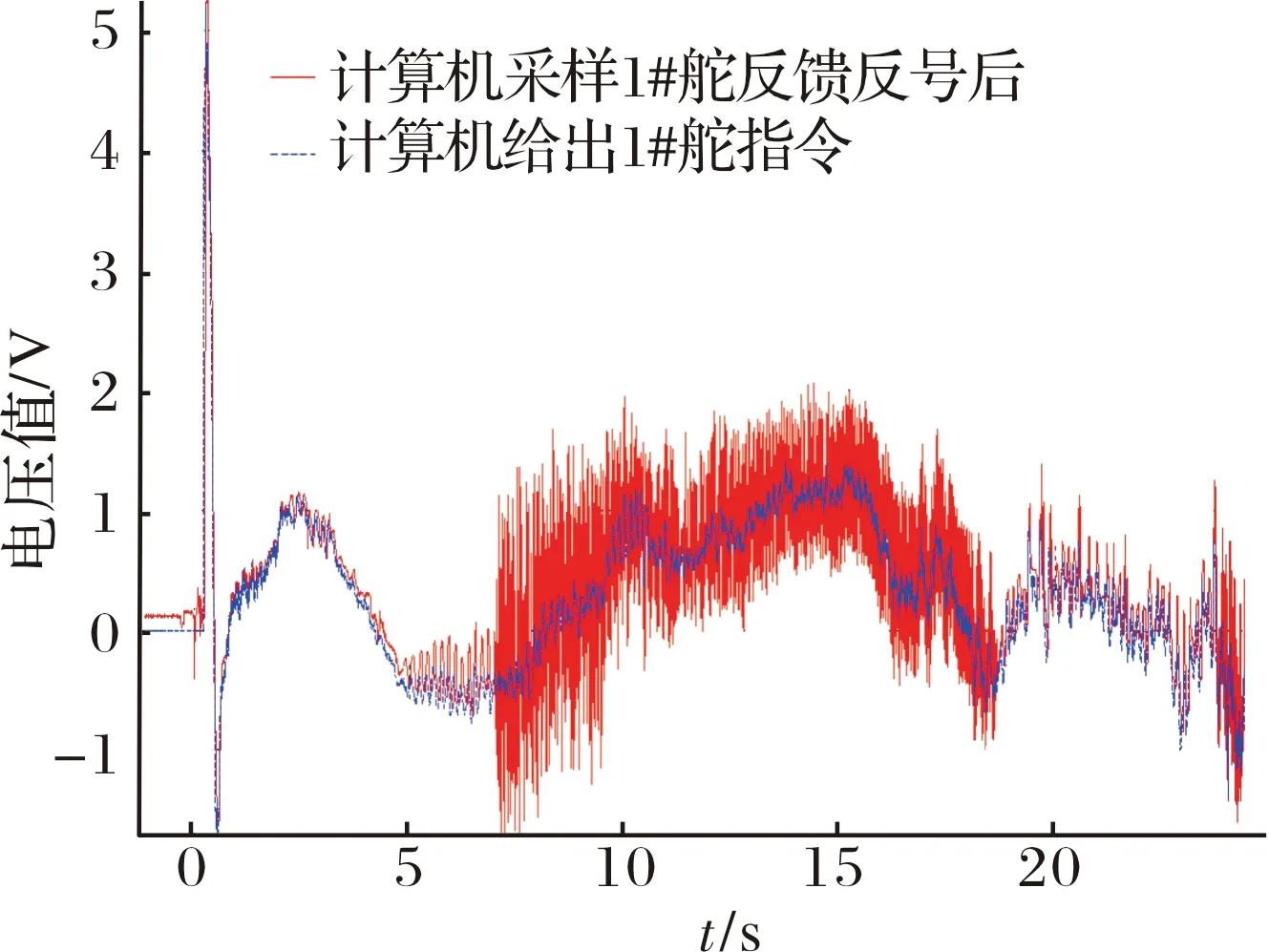
图13 舵指令和舵反馈示意图
舵面在发动机关闭后变现处的高频抖动,其非定常脉动载荷激励的来源为弹体底部非定常流动。这为工程实际中寻找舵面高频振动的来源以及研究抑制舵面高频振动的方法提供了参考。
3.3 流场涡结构的分析
图14为3种分析模型流场中涡量等值面云图。对于单独舵面模型,分离涡结构相对较简单;对于原始模型,底部分离区域和分离涡尺度均较大,舵面根部处分离涡结构和弹体底部上的分离涡存在相互干扰;对于弹身加长模型,舵面根部处分离涡结构和弹身处的局部较小的分离涡存在相互干扰。这也从分离涡结构角度解释了仅仅考虑弹身对舵面的干扰,脉动幅值有一定程度的增加,而当进一步考虑弹体底部影响后,舵面上非定常气动力脉动幅值将大幅增加。
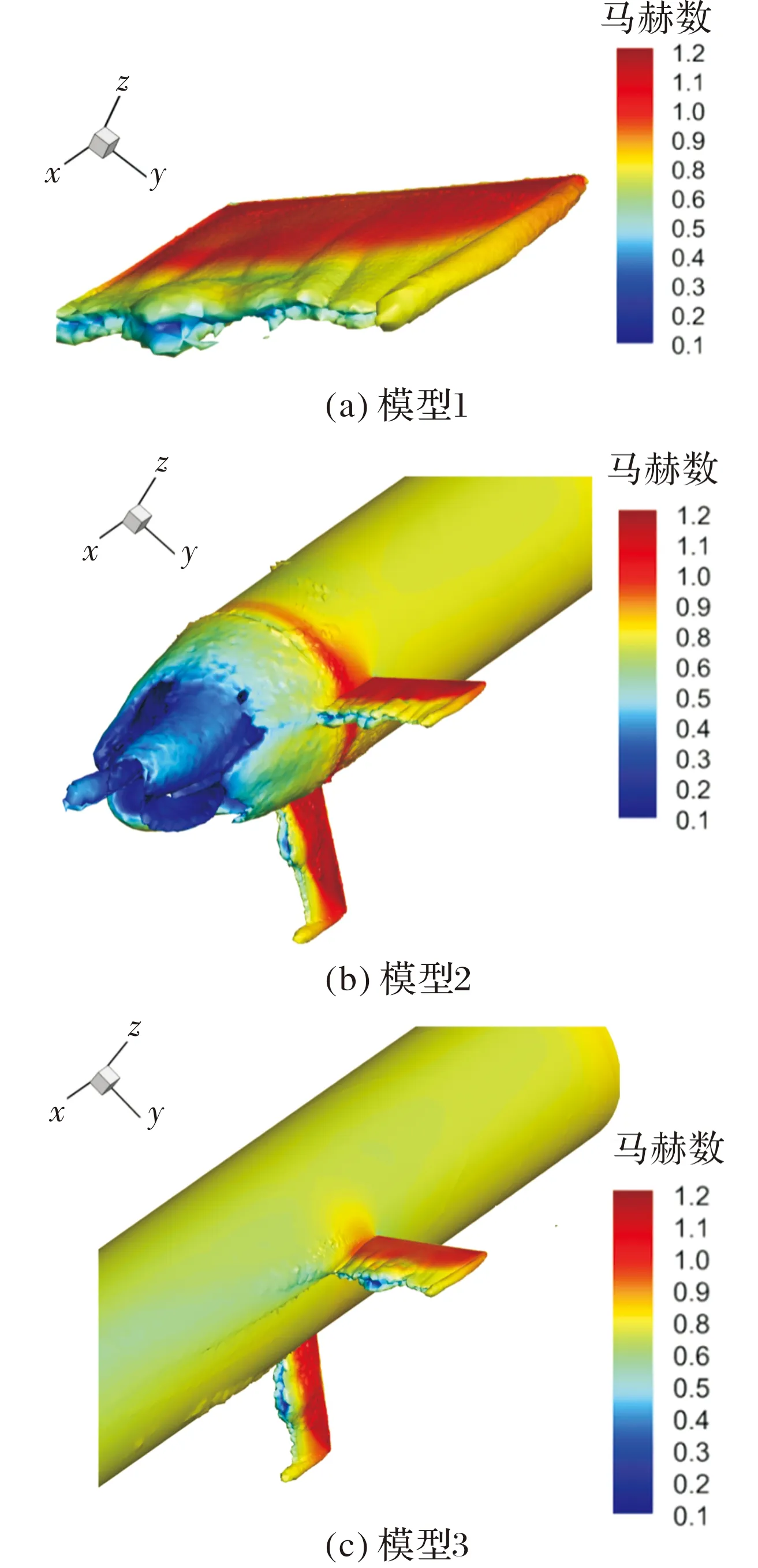
图14 非定常流场涡量等值面
4 结论
从气动的角度研究亚声速舵面高频振动的原因,基于CFD技术求解URANS方程,对3种模型进行非定常数值模拟。通过对不同模型下舵面非定常气动力脉动幅值以及频率的分析,得出以下结论:
1)仅仅考虑弹身对舵面的干扰,将导致舵面上非定常气动力脉动的幅值增加同时主频率也增加。对于模型频谱分析的幅值由6.0增加到14.0,主频率由10 Hz增加到25 Hz。
2)当同时考虑弹身和弹体底部对舵面的干扰,将导致舵面上非定常气动力脉动的幅值进一步大幅增加了,同时主频率也会进一步增加。对于分析模型,频谱分析的幅值由6.0增加到30.0,主频率由10 Hz增加到30 Hz。
文中揭示舵面在发动机关闭后变现处的高频抖动机理,发现其非定常脉动载荷激励的来源主要为弹体底部非定常流动。这对从工程中寻找舵面高频振动的来源以及研究抑制舵面高频振动的方法提供了参考。
