基于时滞稳定裕度的柔性直流系统高频稳定性分析

张 芳，杨丰瑜，姚文鹏

（智能电网教育部重点实验室（天津大学），天津 300072）

基于模块化多电平换流器的高压直流MMCHVDC（modular multilevel converter based high voltage direct current）输电系统因其结构灵活，有功无功实现解耦控制，谐波含量低等优势在海上风电场并网等领域得到了广泛应用[1-2]。近年来，国内多处柔直工程已经出现交流系统与柔直换流站间的高频振荡现象，如2017年鲁西直流工程柔直换流站经弱电网接入交流电网时，出现1 270 Hz的高频振荡；2018年渝鄂背靠背联网工程在加压调试的过程中出现700 Hz和1 810 Hz左右的高频振荡[3-5]。

针对MMC-HVDC系统的高频振荡，国内外学者采用阻抗法开展了一系列的研究。文献[4-5]建立了MMC换流站和交流系统的阻抗模型，分别复现了鲁西1 270 Hz和渝鄂1 810 Hz的高频振荡现象，分析了高频振荡的产生机理；文献[6-7]采用阻抗法，利用广义奈奎斯特稳定判据分析影响高频振荡的关键环节。文献[6]建立了MMC-HVDC系统的阻抗模型，分析了延时大小、锁相环参数、电压前馈环节和运行功率对高频振荡的作用规律；文献[7]基于阻抗模型，证明了控制器中的链路延时是导致换流器阻抗在高频段呈现负电阻的原因，且无论电压源型换流器的拓扑结构如何，长延时都会产生高频负阻抗。阻抗法虽然计算和分析过程简单直观，便于分析高频振荡产生的机理，但柔性直流系统主要采用简化阻抗模型，故分析结果存在一定的误差，且阻抗法依赖于交流系统阻抗模型，而实际工程中外部交流系统复杂，且随运行方式变化，交流系统的阻抗模型不易获取。

除阻抗法外，状态空间法也被广泛应用于高频稳定性的分析，状态空间法通过构建状态空间模型，结合根轨迹分析系统高频稳定性。文献[8]基于状态空间模型采用特征值法分析了高频振荡的机理，指出采样延时是导致渝鄂工程中出现1 810 Hz高频振荡的原因；文献[9]提出了衡量系统小扰动稳定性强弱的临界角度指标和衡量变量对系统稳定性影响大小的影响强度指标，基于参数的影响强度指标揭示了时滞是系统出现Hopf分岔现象的根本原因；文献[10]研究了延时环节时间常数对MMCHVDC高频振荡的影响，指出了交流系统和MMC的延时环节间的耦合作用是导致系统发生高频振荡的主要因素；文献[11]建立了MMC-HVDC系统的谐波状态空间模型，研究了交流网络参数、链路延时时间和控制器参数对高频振荡的影响；文献[12]通过参与因子分析辨识了引起高频振荡的关键因素，利用根轨迹法分析了锁相环、内环电流控制器参数、交流线路参数以及并联回路数等交流系统参数对高频稳定性的作用；文献[13]结合阻抗法和状态空间法两种方法的优点，分别建立了MMC-HVDC系统的阻抗模型和状态空间模型，基于状态空间法分析了影响高频振荡的关键因素，基于阻抗法揭示高频振荡产生的机理。

上述文献在利用状态空间法分析高频振荡的影响因素时通常采用Pade变换对延时环节进行等效，采用Pade变换会引入新的特征根，新引入的特征根可能会与系统原有特征根产生交互作用，对分析结果产生影响。此外，Pade变换是一种有差变换，误差与Pade变换的阶数相关，阶数越大，误差越小；而状态空间模型的复杂度会随着Pade变换阶数的增加而增大，因此合理选取Pade变换的阶数，平衡状态空间模型的精确度与复杂度存在一定的困难[14]。Rekasius变换是时滞系统稳定性分析中常用的处理超越项的手段，一方面引入Rekasius变换后可不带任何近似地求解系统时滞稳定裕度；另一方面在给定系统参数下，基于Rekasius变换可直接计算系统时滞稳定裕度，而Pade变换则需不断改变延时时间求取稳定裕度。相较于Pade变换，引入Rekasius变换分析结果更精确，分析过程更简便。

本文考虑延时的MMC-HVDC系统视为典型的时滞系统，从时滞系统小扰动稳定性的角度研究MMC-HVDC系统的高频稳定性，推导建立系统的时滞微分方程模型，利用Rekasius变换精确求解MMC-HVDC系统的时滞稳定裕度，基于时滞稳定裕度定量分析MMC-HVDC系统高频振荡的影响因素。本文所做工作为研究柔性直流输电系统高频稳定性及分析高频振荡的影响因素提供了新的思路。

1 考虑系统延时的MMC-HVDC系统模型

MMC-HVDC系统主电路及控制系统结构如图1所示。将MMC-HVDC系统分为主电路数学模型和控制系统数学模型两部分，采用将主电路建模在以同步转速ω1旋转的同步d-q坐标系下、将控制系统建模在以锁相环测量转速ωPLL旋转的控制dcf-qcf坐标系下的建模方法。

图1 MMC-HVDC系统主电路及控制系统结构Fig.1 Structure of main circuit and control system for MMC-HVDC system

1.1 主电路数学模型

主电路数学模型均建立在以同步转速ω1旋转的同步坐标系下，由图1可知，MMC-HVDC系统主电路数学模型为

式（1）和式（2）的线性化模型为

1.2 控制系统数学模型

MMC-HVDC控制系统主要由外环功率控制、锁相环、内环电流控制、电压调制和环流抑制等环节构成，实际柔直工程实例和文献表明，外环功率控制、环流抑制和换流站内部动态特性对系统高频稳定性影响较小[12，15]，因此本文在建模时忽略外环功率控制、环流抑制环节及MMC内部动态，仅考虑锁相环、内环电流控制和电压调制环节。

1）同步坐标系和控制坐标系之间的关系

图2 MMC-HVDC系统坐标系Fig.2 Coordinate system for MMC-HVDC system

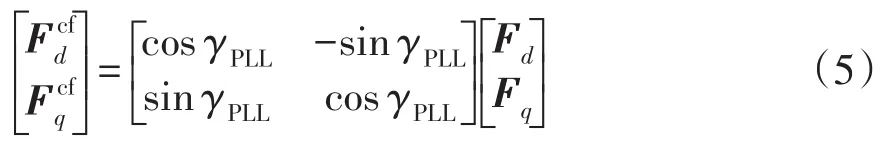
由图2可知

式（5）和式（6）的线性化模型为

式中：Fd0和Fq0分别为相量F在系统平衡点处的d、q轴分量；Δ为线性化模型变量参数。

2）锁相环的数学模型

锁相环控制结构如图3所示。

图3 锁相环结构框图Fig.3 Block diagram of PLL structure

式中，Kp_PLL和Ki_PLL分别为锁相环PI控制中的比例系数和积分系数。

式（8）的线性化模型为

3）内环电流控制的数学模型

定义d轴和q轴交流电流参考值与实际值之差为经内环电流PI控制中的积分环节后引入的变量为xid和xiq，则有内环电流控制的数学模型为

式（10）和式（11）的线性化模型为

4）电压调制过程

式（14）的线性化模型为

1.3 MMC-HVDC时滞微分方程模型

利用式（7）将上述线性化模型中dcf-qcf坐标系下的变量都转换到d-q坐标系下，利用代数方程消去微分方程中的代数变量Δusd、Δusq、Δucd和Δucq，得到MMC-HVDC系统时滞微分方程模型为

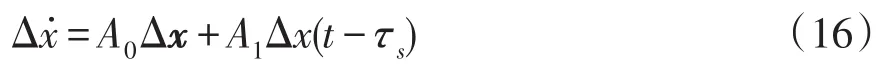
式中：Δx为常规状态变量构成的向量；Δx(t-τs)为对应的时滞状态变量构成的向量；A0为常规状态变量矩阵；A1为时滞状态变量矩阵。各量分别表示为

式中：Usd0、Usq0、Ucd0和Ucq0分别为PCC点电压和换流器调制点电压在系统平衡点处的d、q轴分量；Icd0和Icq0分别为交流电流在系统平衡点处的d、q轴分量。

式（16）所示的MMC-HVDC系统微分方程数学模型是时滞系统稳定性分析中常用的标准形式。

由式（16）可知，MMC-HVDC时滞系统的特征方程为

求解式（20）得到MMC-HVDC系统的特征根。如果系统的所有特征根均位于复平面的左半平面，则对于时滞时间τs，MMC-HVDC系统是小扰动稳定的；如果除1对位于虚轴上的纯虚特征根s=±jω外，系统所有特征根均位于复平面的左半平面，则对于时滞时间τs，MMC-HVDC系统处于临界稳定状态；如果系统存在位于右半平面的特征根，则对于时滞时间τs，MMC-HVDC系统是小扰动不稳定的。

时滞稳定裕度是指系统在保证小扰动稳定的前提下，能够承受的最大时滞时间。文献[18]指出，控制链路延时是造成柔性直流输电系统高频振荡的重要因素。式（16）所表示的MMC-HVDC系统是一个单时滞系统，当系统总延时τs大于时滞稳定裕度时，MMC-HVDC系统会发生高频振荡现象。因此，系统时滞稳定裕度越大，表示系统所能承受的链路延时时间越长，系统高频稳定性越好。本文将结合Rekasius变换求解系统的时滞稳定裕度，基于时滞稳定裕度分析MMC-HVDC系统高频振荡的影响因素。

2 基于Rekasius变换求解MMC-HVDC系统时滞稳定裕度

2.1 Rekasius变换

Rekasius变换[19]表示为

式中：T为待求变换系数，且T∈R；当τs∈R+，s为纯虚特征根，设s=jωv（ωv为系统角频率）时存在唯一的T与之对应，使得式（22）为恒等变换。

将式（22）替换式（21）中的超越项，即可得指数方程转化为多项式方程，即

式中，bm为与T相关的实系数。

由Rekasius变换的性质可知，式（23）的纯虚特征根即为式（21）的纯虚特征根。不断改变系数T，求解式（23）的特征根，当特征多项式存在纯虚特征根s=jωv时，求解系统此时的时滞常数为

由式（21）可知，一个纯虚特征根s=jωv对应一个频率ωv，同时对应无数个时滞常数τvl。将式（24）求解得到的所有时滞常数记为集合Mτv，表示为

求出式（20）中的所有纯虚特征根，并根据式（24）计算出对应每一个纯虚特征根的时滞常数集合。由系统时滞稳定裕度的定义可知，所有时滞常数集合中最小的正时滞常数即为式（21）所示系统的时滞稳定裕度。

求解系统时滞稳定裕度时，为了减少计算量，可以利用劳斯判据判断系统是否存在纯虚特征根。

2.2 劳斯判据

由劳斯判据[20]可知，劳斯表中第1列系数全为正时，系统稳定；劳斯表中第1列各系数符号的改变次数Ns即为特征方程的正实部特征根个数。

由于bm与变换系数T相关，因此随着T的改变，由式（23）形成的劳斯表也将发生变化。设有u个T会使得劳斯表中第1列系数符号的改变次数发生变化，记为集合N={T1,T2,…,Tu}，集合N中的每一个元素都使得式（23）存在一对纯虚特征根。因此，利用劳斯判据，得到集合N后即可利用成熟的多项式特征根求解方法求解式（23）的所有纯虚特征根。

2.3 求解MMC-HVDC系统时滞稳定裕度的步骤

综上，求解MMC-HVDC系统时滞稳定裕度的步骤如下。

步骤2 给定变换系数T，T∈（-∞，+∞），利用劳斯判据判断在当前T下按照式（23）形成的劳斯表中第1列各系数符号的改变次数是否发生变化。若是，转入步骤3；若否，则转入步骤4。

步骤4 改变变换系数T，重复步骤2，直至找到系统所有的纯虚特征根后，所有时滞常数集合中最小的正时滞常数即为式（21）所示系统的时滞稳定裕度。

基于Rekasius变换求解系统时滞稳定裕度流程如图4所示。

图4 基于Rekasius变换求解系统时滞稳定裕度的流程Fig.4 Flow chart for solving the delay stability margin of system based on Rekasius transform

3 基于时滞稳定裕度分析MMC-HVDC系统高频振荡的影响因素

在PSCAD平台中搭建如图1所示的MMCHVDC系统模型，整流侧换流站采用定有功功率和定无功功率控制，MMC-HVDC系统主电路参数和控制系统参数分别如表1和表2所示。

表1 MMC-HVDC系统主电路参数Tab.1 Parameters of main circuit for MMC-HVDC system

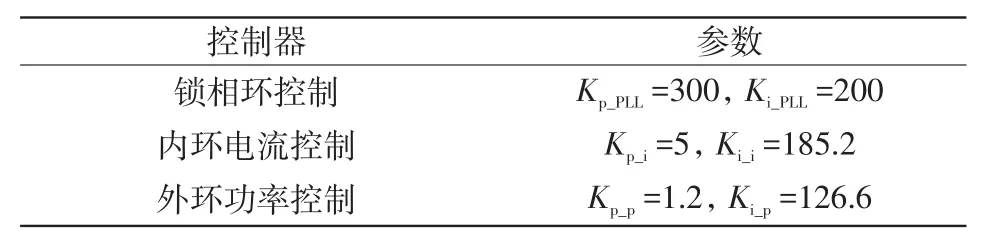
表2 MMC-HVDC系统控制系统参数Tab.2 Parameters of control system for MMC-HVDC system

考虑延时的MMC-HVDC系统小扰动稳定的前提是系统总延时τs小于系统的时滞稳定裕度，而系统总延时与MMC-HVDC系统高频段特性密切相关[4]，时滞稳定裕度越大，MMC-HVDC系统能够承受的系统总延时越长，系统高频稳定性越好；反之，时滞稳定裕度越小，MMC-HVDC系统能够承受的系统总延时越短，系统高频稳定性越差，越容易发生高频振荡。基于式（16）建立的MMC-HVDC系统模型，利用Rekasius变换求解系统时滞稳定裕度，并根据时滞稳定裕度大小分析MMC-HVDC系统控制器参数及直流系统功率传输水平对MMC-HVDC系统高频稳定性的影响。

3.1 控制器参数对高频稳定性的影响分析

由矩阵 A0、A1和式（20）可知，MMC-HVDC系统的特征方程与控制器参数有关，控制器参数将会影响系统时滞稳定裕度，因此本节针对控制器参数对MMC-HVDC系统高频振荡的影响进行分析。

1）内环电流比例系数

设内环电流比例系数Kp_i=5，根据第2.3节的步骤求解系统时滞稳定裕度。在变换系数T∈[0，0.000 2）时，系统特征方程对应的罗斯表中第1列元素全为正，第1列元素符号改变次数Ns=0；T∈[0.000 2，0.000 23]时，系统特征方程对应的劳斯表中第1列元素符号改变次数Ns与变换系数T的关系曲线如图5所示。

由图5可知，在T1=2.137 8×10-4时，Ns由0变为2，此时系统有一对特征根穿越虚轴进入右半平面；在T2=2.151 3×10-4时，Ns由2变为4，此时系统又有一对特征根穿越虚轴进入右半平面。根据式（24）求解对应T=T1和T=T2的系统最小正时滞常数分别为：τ1_min=345.52 μs；τ2_min=328.81 μs。

图5 Ns与变换系数T的关系Fig.5 Relationship betweenNsand transform factor T

继续增大T，Ns始终保持为4不变，系统不再有特征根穿越虚轴进入右半平面。因此，Kp_i=5时，系统时滞稳定裕度为 τs=τ2_min=328.81 μs，此时系统的纯虚根为s=0±j4 997.4，角频率为 ω1=4 997.4 rad/s，振荡频率为795.4 Hz。

以0.5为步长，将内环电流比例系数Kp_i由5逐步增大至10，重复上述步骤，得到不同Kp_i下的系统时滞稳定裕度及纯虚特征根振荡频率，如表3所示，系统时滞稳定裕度随Kp_i的变化曲线如图6所示。

表3 不同Kp_i下的系统时滞稳定裕度及纯虚根振荡频率Tab.3 Delay stability margin of system and the oscillation frequency of pure imaginary root with different values ofKp_i

图6 不同Kp_i下的系统时滞稳定裕度Fig.6 Delay stability margin of system with different values ofKp_i

由表3可知，内环电流比例系数Kp_i对MMCHVDC系统高频稳定性有显著影响。Kp_i由5增大到10，系统时滞稳定裕度由328.81 μs减小至167.02 μs，减小49.2%；系统振荡频率由795.4Hz增大至1 532.9 Hz，增大92.7%；随着Kp_i增大，系统时滞稳定裕度减小，考虑系统延时的MMC-HVDC系统小扰动稳定性变差，发生高频振荡的风险提升。因此，适当减小内环电流比例系数有利于改善MMC-HVDC系统的高频稳定性。

2）内环电流积分系数

固定Kp_i=5不变，以5为步长，将内环电流积分系数Ki_i逐步由135.2增大到185.2，不同Ki_i下系统时滞稳定裕度及纯虚特征根振荡频率如表4所示。

表4 不同Ki_i下的系统时滞稳定裕度及纯虚根振荡频率Tab.4 Delay stability margin of system and the oscillation frequency of pure imaginary root with different values ofKi_i

由表4可知，电流内环积分系数由135.2增大到185.2，系统时滞稳定裕度由329.15 μs缓慢减小至328.81 μs，减小0.1%，基本不变；系统振荡频率由795.5 Hz减小至795.4 Hz，基本保持不变。由此可见，改变内环电流积分系数Ki_i对MMC-HVDC系统高频稳定性基本无影响。

3）锁相环参数

将锁相环的比例系数Kp_PLL与积分系数Ki_PLL的比值固定在1.5不变，以20为步长，将Kp_PLL由200逐步增大到400，不同Kp_PLL下的系统时滞稳定裕度及纯虚特征根振荡频率如表5所示。

由表5可知，锁相环参数Kp_PLL由200逐步增大到400、Ki_PLL由133.3逐步增大到266.7的变化过程中，系统时滞稳定裕度由328.61 μs增大至328.98 μs，增大0.1%，基本不变；振荡频率由795.8 Hz减小到794.9 Hz，基本不变。由此可见，改变锁相环参数对MMC-HVDC系统高频稳定性基本无影响。

表5 不同PLL参数下的系统时滞稳定裕度及纯虚根振荡频率Tab.5 Delay stability margin of system and the oscillation frequency of pure imaginary root with different PLL parameters

综合上述理论分析的结果，内环电流比例系数对系统高频稳定性影响显著，随着内环比例系数的增大，系统发生高频振荡的风险增加；而内环电流积分系数和锁相环参数对系统的高频稳定性影响不大。

3.2 有功、无功功率变化对高频稳定性的影响分析

1）有功功率变化

MMC-HVDC系统在实际运行中需要调制直流功率以参与电网的稳定控制，因此本节研究有功功率变化对高频稳定性的影响。

保持无功功率参考值Qref=0，以0.125 p.u.为步长，将有功功率参考值Pref从-1 p.u.逐步增大到1 p.u.，不同Pref下的系统时滞稳定裕度及纯虚特征根振荡频率如表6所示。

表6 不同Pref下的系统时滞稳定裕度及纯虚根振荡频率Tab.6 Delay stability margin of system and the oscillation frequency of pure imaginary root with different values ofPref

由表6可知，有功功率变化对系统高频稳定性略有影响，有功功率参考值Pref由-1 p.u.逐渐增大至1 p.u.，系统时滞稳定裕度由327.96 μs逐步增大到328.81 μs，增大0.3%；振荡频率由797.5 Hz减小到795.4 Hz，减小0.3%。随着换流站由逆变状态变化到整流状态，系统时滞稳定裕度略有增大，因此换流站运行在整流状态时的高频稳定性要略优于运行在逆变状态。

2）无功功率变化

MMC-HVDC系统在运行的过程中需调节无功功率以维持交流电压的恒定，因此本节探究无功功率变化对系统高频稳定性的影响。

保持有功功率参考值Pref=1.0 p.u.，以0.125 p.u.为步长，将无功功率参考值Qref从-0.5 p.u.逐步增大到0.5 p.u.，不同Qref下的系统时滞稳定裕度及振荡频率如表7所示。

表7 不同Qref下的系统时滞稳定裕度及纯虚根振荡频率Tab.7 Delay stability margin of system and the oscillation frequency of pure imaginary root with different values ofQref

由表7可知，无功功率变化对系统高频稳定性几乎无影响，无功功率参考值Qref由-0.5 p.u.逐渐增大至0.5 p.u.，系统时滞稳定裕度由328.95 μs逐步减小到328.64 μs，减小0.09%；振荡频率由795.3 Hz增大到795.4 Hz，基本不变。因此无功功率变化对MMC-HVDC系统高频稳定性几乎无影响。

4 时域仿真验证

基于PSCAD仿真平台搭建图1所示系统仿真模型对第3节中的结论进行仿真验证。仿真中MMC最近电平逼近调制NLM（nearest level modulation）的延时为150～160 μs，系统总延时考虑NLM调制延时设置为155 μs。

首先验证内环比例系数对系统高频稳定性的影响，设置系统总延时为237 μs，由表3可知，237 μs为Kp_i=7时的系统时滞稳定裕度。t=1.0 s时，电流内环比例系数由5增大至7，交流电流和d轴电流仿真波形分别如图7（a）所示，取1.5 s至2.0 s的d轴电流数据进行傅里叶分解，傅里叶分解结果如图7（b）所示。

图7 内环电流比例系数变化时的仿真结果Fig.7 Simulation results with changes in proportionality coefficient of inner loop current controller

由图6可知，1.0 s前，比例系数Kp_i=5时系统稳定运行，没有发生高频振荡；1.0 s之后，比例系数Kp_i变为7，系统发生高频振荡，时域仿真得到的d轴电流振荡频率为1 060 Hz，该振荡频率与理论分析得到的1 090.3 Hz相差30.3 Hz，理论计算结果与仿真吻合较好。

为验证内环电流积分系数对高频稳定性的影响，设置系统总延时为310 μs，比例系数Kp_i=5，t=1.0 s时电流内环积分系数Ki_i由140增大至180。

图8为内环电流积分系数变化时系统交流电流和内环d轴电流时域仿真波形，内环电流积分系数变化前后，系统均处于稳定状态，电流波形中无高频分量，验证了前文理论分析的正确性；同时，电流积分系数Ki_i由140增大至180，发生较大变化，但电流波形无明显畸变，说明内环电流积分系数对系统时滞稳定裕度影响不大，与理论分析结论一致。

图8 内环电流积分系数变化时的仿真结果Fig.8 Simulation results with changes in integration coefficient of inner loop current controller

图9为锁相环参数变化时系统交流电流和内环d轴电流时域仿真波形，设置系统总延时为310 μs，t=1.0 s时锁相环比例系数Kp_PLL由200增大至300。由图9可知，锁相环参数变化前后，系统均处于稳定状态，电流波形中无高频分量。仿真波形说明锁相环参数对系统时滞稳定裕度影响不大，与理论分析结论一致。

图9 锁相环参数变化时的时域仿真结果Fig.9 Simulation results in time-domain with changes in PLL parameters

图10为有功功率变化时系统交流电流和内环d轴电流的时域仿真波形，设置系统总延时为310 μs，t=1.0 s时有功功率参考值 Pref由1 p.u.变为-1 p.u.，MMC换流站由整流状态转为逆变状态。有功功率变化后，谐波畸变率由1.04%变为1.22%，由于有功功率变化前后系统总延时小于系统时滞稳定裕度（分别为328.81 μs和327.96 μs），因此系统未发生高频振荡。

图10 有功功率参考值变化时的时域仿真结果Fig.10 Simulation results in time domain with changes in reference value of active power

图11为无功功率变化时系统交流电流和内环q轴电流的时域仿真波形，设置系统总延时为310 μs，t=1.0 s时，无功功率参考值 Qref由-0.2 p.u.变为0.2 p.u.，无功功率变化后，系统稳态运行点改变，因此q轴电流经历短暂的暂态过程后趋于稳定，无功功率变化后q轴电流和交流电流均未发生明显畸变，系统仍处于稳定状态。

图11 无功功率参考值变化时的时域仿真结果Fig.11 Simulation results in time domain with changes in reference value of reactive power

5 结论

本文建立了考虑系统延时的柔性直流输电系统数学模型，结合Rekasius变换求解系统时滞稳定裕度，基于时滞稳定裕度研究了高频稳定性的影响因素，结论如下。

（1）本文采用Rekasius变换消去MMC-HVDC系统特征方程中的超越项，相较于Pade近似，Rekasius变换表达式在纯虚根处是恒等变换，因此采用Rekasius变换分析结果更精确可靠；此外，Pade近似需不断改变延时时间反复求解特征根来确定时滞稳定裕度，而本文引入Rekasius变换后可直接求解系统时滞稳定裕度，分析过程更简便。本文基于时滞稳定裕度的高频稳定性分析方法为MMCHVDC系统高频稳定性分析提供了新思路。

（2）内环电流比例系数是影响MMC-HVDC系统高频稳定性的重要因素，减小内环电流比例系数能够提高系统的高频稳定性。系统有功功率变化对高频稳定性略有影响，工作在整流状态时系统的高频稳定性要优于工作在逆变状态。内环电流积分系数、锁相环参数和无功功率变化对系统高频稳定性几乎无影响。

（3）系统时滞稳定裕度反映了系统的高频稳定性强弱，下一步工作可研究系统高频振荡的抑制策略，从增大系统时滞稳定裕度的角度改善控制器结构、选取控制器参数来抑制高频振荡。