微细磨削表面成型机理的研究浅析

陶瓷材料由于其具有高熔点、高硬度、高耐磨性、耐氧化性及绝缘性而广泛应用于航空航天、电子电气、医学等领域。与此同时，对于由陶瓷材料制作成的微细部件的市场需求也在日益增加，但是，考虑到陶瓷材料本身属于硬脆的难加工材料，很难使用普通的加工方式对其进行加工，这也引起了微细磨削工艺在加工陶瓷材料领域的巨大发展。比如，使用微细笔状磨削刀具或者超薄刀片的微细磨削加工。与以其他刀具为基础的微细加工工艺相比较而言，微细磨削在加工硬脆材料时有若干优点。

改革开放以来，我国规划工作取得重大进展，国土空间规划取得积极成效，但规划编制工作仍存在一些问题。经济社会发展转型必然对空间优化提出相应需求。高质量发展落实到国土空间上，要通过高质量规划实现国土空间高质量开发利用，保障和促进经济高质量发展。

微细笔状磨削刀具相较雕刻机而言的优点在于可以灵活地生产复杂三维微观结构。磨削刀具上的磨料颗粒通过多种物理或者化学方法被覆盖在圆柱型的基体上，比如，电镀、化学镀、电铸、冷喷涂及CVD(化学气相沉积)。与传统的砂轮相类似的是，无论是哪种方法，磨粒的位置与方向都是随机的。在材料去除机理方面，传统磨削加工与微细磨削加工是一定可比性的，也就是说，单独一个磨粒在与工件表面的切割去料过程中所引起的摩擦、耕犁、剪切变形的模式是可比较的。与基于其他刀具的微细加工工艺相类似，与最小磨屑厚度相关联的尺寸效应起着重要的作用。表1中着重对比了传统磨削工艺与微细磨削工艺的加工环境。

从表1中可以明显看出，微细磨削的切削速度要远远小于传统磨削中的切削速度。在传统磨削中较低的速度比导致单个磨粒拥有更高的进给量及更大的进给角度，这影响着参与磨削的磨粒总数。这里将单个磨粒的进给量定义为，磨粒在一次旋转中所经过的距离。沿着切削路径上任意位置的影响程度是由进给角度所决定的，而进给角度的计算要考虑到砂轮圆周速度矢量与工件速度矢量。

如果在砂轮表面有

个均匀分布的磨粒，那么对每一个磨粒(假设为第

个磨粒)的进给量(

)、位移接触长度(

)和进给角(

)的数值都可以由公式(1)-(3)计算得出。

实值RBM模型相对于二值RBM模型就是将评分数据表示为多维度的0、1向量，以满分5分为例，则在表示评分的向量中第五行为1向量，其他行都为0向量，没有评分即所有的行都为0表示，此方法虽然会在一定程度上导致数据量变大，但是可以很有效地解决多评分问题。具体实值RBM模型如图1所示。

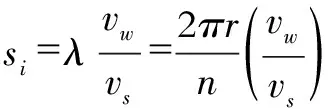
(1)

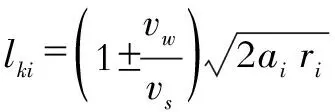
(2)

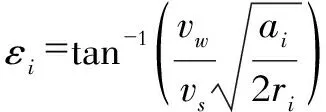
(3)

式中，

为砂轮表面两个相邻磨粒间的距离，

为第

个磨粒的切削深度，

为砂轮半径，

为第

个磨粒的径向高度。径向高度是指从砂轮中心到磨粒切割点之间的距离。如果将第

个磨粒与其他磨粒间的相互作用忽略不计，那么公式(1)中的

值等于2

。

已经有学者对磨削过程中的力学特性及磨削过程中相应预测的有限元模型、多比例模型进行了一些分析工作。大部分关于微细磨削过程相应的推测的分析工作都考虑到了Makin的均匀砂轮表面模型(公式(4))和表2中总结的静态切割边缘密度。

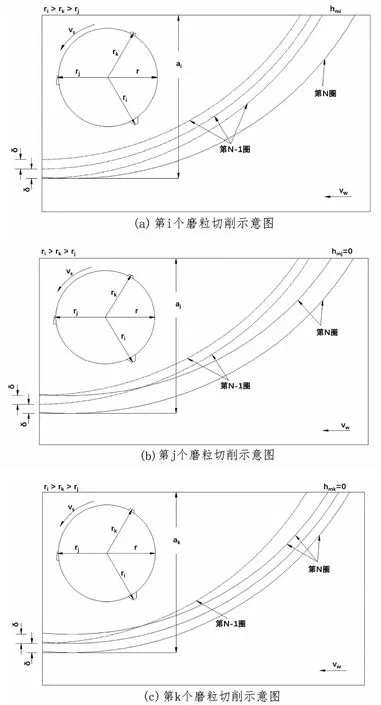
砂轮表面参与磨削的磨粒百分比与未变形磨屑的平均厚度是影响加工表面质量的主要因素。未变形磨屑厚度(hmi)是指单独一个磨粒切削的最大深度。它取决于多种因素，包括砂轮表面质量与运动学条件。对于传统磨削而言，已经发表了关于未变形磨屑尺寸估算的若干描述。根据Malkin的理论，对于一个表面形状均匀的砂轮而言，单个磨粒的最大切削深度(假设为第i个磨粒，图1a)可以描述为：

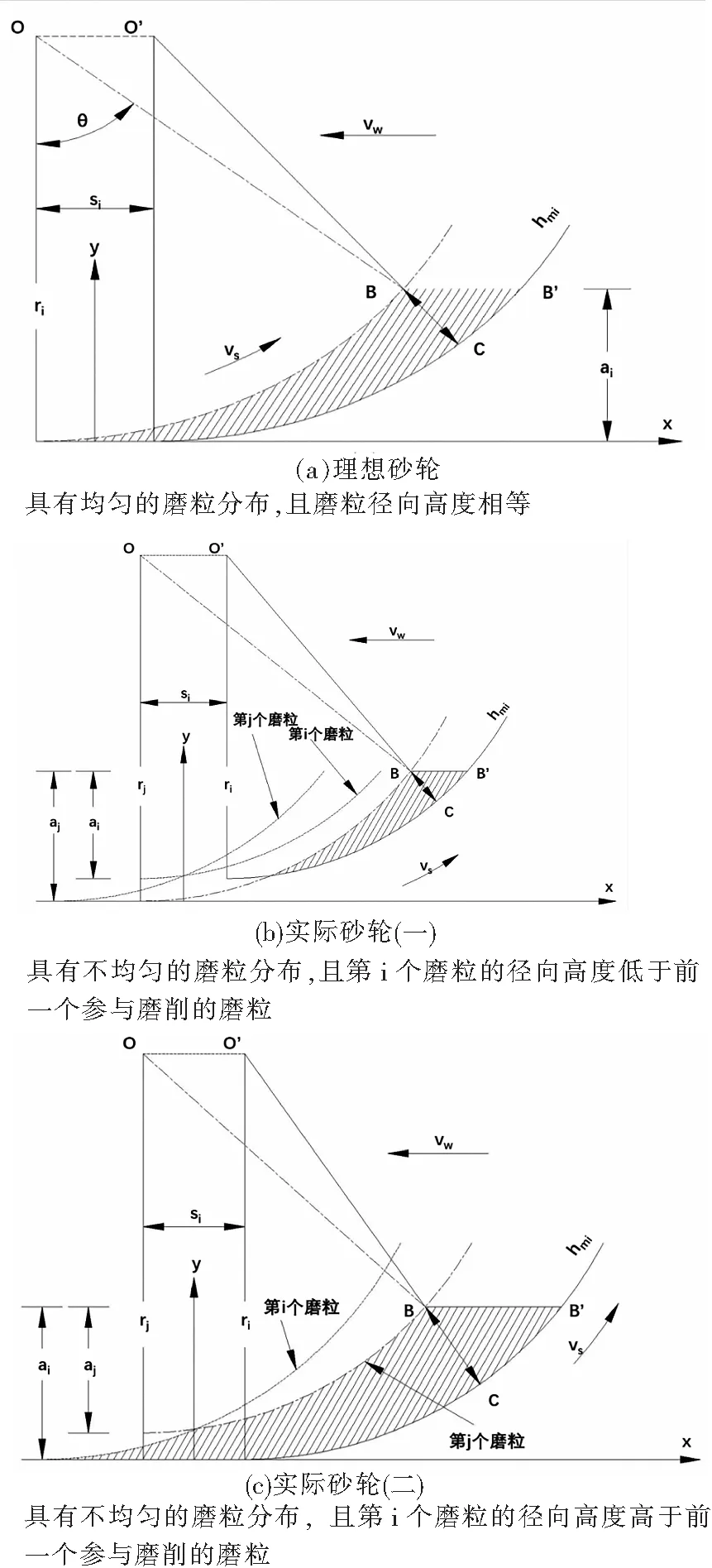
图2中展示了一个案例，案例中的砂轮表面仅有三个磨粒(

，

和

)。这三个磨粒彼此间距离相等，并且处于同一轴向平面内。相邻的两个磨粒间的距离是恒定的(即：

=

=

=

)，并且径向高度差的关系为：

=

-

，2

=

-

，

=

-

。给定一个旋转方向，

是

的前一个磨粒，

是

的前一个磨粒，

是

的前一个磨粒。在所有的案例中，拥有最大径向高度的磨粒(即第

个磨粒)是进入切削区域的第一颗磨粒(或者是前导磨粒)。在这些条件下，根据公式(6)，对应每一个磨屑的未变形磨屑厚度值可由以下公式表示(图2

-

)。

对于一个表面形状不均匀的砂轮而言(即，磨粒的分布与凸起都不均匀，图1

-

)，根据下方公式(6)可得出第

个磨粒的最大未变形磨屑厚度的值。

(4)

公式(4)在不考虑二阶项并忽略掉那些结果比单位值小得多的项(即数据远小于1的项)可以进一步简化描述为：

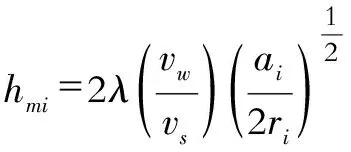
(5)

数据来源：华杨大队：《一九七三年收益分配统计表》，《一九七五年收益分配统计表》，《一九七九年收益分配统计表》，高县档案馆藏。

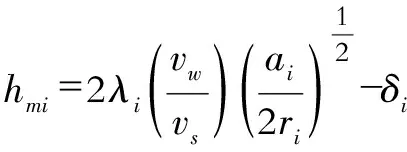
(6)

式中

为砂轮表面即将参与磨削加工的磨粒(第

个)与前一个磨粒(第

个)之间的距离，

为前一个磨粒的切削深度，

为两个磨粒之间的高度差(

-

)，当即将到来的磨粒凸起高度小于前一个磨粒

为正值，反之则为负值。如果

为负值，即将参与磨削加工的磨粒将不会进行切削，可忽略。

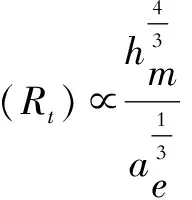
(7)

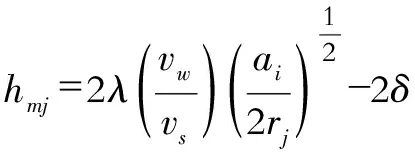
(8)

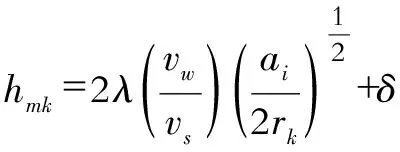
(9)

从公式(9)中可以很明显的看出，尽管理论切削厚度值是正的，但是正如图2c中所展现的最大径向高度磨粒的运动轨迹，第k个磨粒的实际切屑厚度值是小于零的。此外，Malkin的模型(公式(6))仅仅只考虑了即将参与磨削加工的磨粒和前一个磨粒之间的径向高度差。但是，前一个磨粒不一定是一个参与切削的磨粒。此外，从磨粒的运动轨迹可以观察出，即将参与磨削加工的磨粒的未变形磨屑厚度值是由最大径向高度磨粒所决定的。很明显公式(6)是有缺陷的，其仅考虑了与前一个磨粒的径向高度差，而忽略了这些磨粒与最大突出磨粒之间的位置关系。此外，公式(7)-(9)考虑到所有情况下的磨屑的形成(当

>0时)，而忽略了未变形磨屑厚度值与所需最小磨屑厚度值(

’)的比较。由于最小磨屑厚度值在微细磨削中起着重要作用，因此有必要去了解切屑厚度变化，并找到一种描述微细磨削中这些值的简单方法。这种方法应该同时考虑砂轮表面磨粒的分布与他们的运动轨迹。

此外，一项深入的文献研究提出若干个根据未变形切屑厚度过程响应的分析预测公式。未变形切屑厚度与过程反馈(如，磨削力，比能和表面粗糙度)之间的基本关系如下所示：

学术研究支撑我国知识产权制度发展四十年........................................................................邓仪友 赵志彬 09.66

(

)

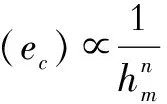
加强林业资源保护力度和完善森林防火管理措施是实现林业资源的可持续发展的根本性措施之一，通过加快我国经济社会产业结构优化升级速度、提高林业资源保护管理机制的全面性、强化林业管理人员的防火意识等来提高林业资源保护效果。

(

)

根据Malkin的理论，在突出点数量相同的情况下，如果切割点比前一个磨粒突出的越多那么该磨粒的未变形切屑厚度尺寸就越大。然而，公式(6)仅仅考虑了静态条件下的砂轮表面特征。并没有考虑到连续切割点的运动学特性。公式(6)的适用性是不确定的，这一点同样在图2中进行了说明。

(

)

根据本组研究结果,我们认为在采用注射器抽吸负压状态下同轴取材活检更容易成功,并且不增加穿刺活检相关并发症,而有助于明确椎体压缩骨折病因,减少椎体压缩骨折病因的误诊和漏诊,使患者获得更长期的良好疗效。因此,经皮椎体成形术中在负压状态下同轴取材活检是一种安全易行、提高诊断准确性的活检方法,应该在椎体压缩骨折行椎体成形术时常规进行。

其他已发表的研究文章都致力于研究通过电镀、化学镀层及CVD等方式研究微细磨削刀具的韧性向脆性的转变，而对微细磨削中砂轮表面的磨粒的运动学分析却是很少报道的。总结过往的研究可以发现，磨粒的运动轨迹和运动学分析对了解微细磨削过程、提升微细磨削工艺水平有着至关重要的决定性作用，后续将通过更多的实验、仿真与数学分析对微细磨削过程中的磨粒运动轨迹建立更加详尽的数学模型以供分析。

结论：

1.微细磨削加工过程中所使用砂轮的外观形貌是不均匀的，每一个磨粒的径向高度不尽相同，所以在研究微细磨削表面成型机理的过程中要注意对不同径向高度的磨粒进行单独分析，以确保计算及分析的正确性。

2.当所研究的磨粒(第i个磨粒)的径向高度低于前一个参与磨削加工的磨粒(第

个磨粒)的径向高度时，则当前磨粒未变形磨屑厚度小于前一个参与磨削加工的磨粒，即

<

。反之，当所研究的磨粒(第

个磨粒)的径向高度高于前一个参与磨削加工的磨粒(第

个磨粒)的径向高度时，则当前磨粒未变形磨屑厚度大于于前一个参与磨削加工的磨粒，即

>

。当

为负值时，所研究的磨粒不参与磨削加工过程。

3.微细磨削是一个动态加工过程，每一个磨粒作为一个单独的个体都有其独有的运动轨迹。所以，在研究微细磨削表面成型机理的过程中，应在考虑静态切削的基础上考虑磨粒的运动轨迹，通过对运动轨迹的分析可以更好的了解各个磨粒之间切削状态的差异，有利于更好地分析微细磨削过程。

培育壮大新动能有利于推进创新发展。创新发展是新发展理念之一。创新是引领发展的第一动力，是建设现代化经济体系的战略支撑。创新发展首先要解决的是创新动力的培育，而培育壮大新动能将为创新发展提供强大的动力。特别是创新型企业是创新发展的基本主体，新技术是创新发展的核心内容，新制度是创新发展的内在动力。

4.微细磨削的砂轮在静态下的外观形貌数据固然重要，但是在设备运转后的加工状态下的运动学数据同样重要。故此，在研究过程中，不能仅仅依赖于实验中所测定的实验数据，同时要考虑各个磨粒在微细磨削加工过程中的动态切削刃。

[1]Gäbler, Jan; Schäfer, Lothar; Menze, Bernd; Hoffmeister, Hans-Werner (2003). Micro abrasive pencils with CVD diamond coating. Diamond and Related Materials, 12(3-7), 707-710. doi:10.1016/S0925-9635(03)00059-1.

[2]J. Ikeno; Y. Tani; A. Fukutani; H. Sato (1991). Development of Chipping-Free Dicing Technology Applying Electrophoretic Deposition of Ultrafine Abrasives. , 40(1), 351-354. doi:10.1016/s0007-8506(07)62004-6.

[3]Hyung Wook Park; Steven Y. Liang (2008). Force modeling of micro-grinding incorporating crystallographic effects. , 48(15), 1658-1667. doi:10.1016/j.ijmachtools.2008.07.004.

[4]J. Cheng, Y.D. Gong, Experimental study of surface generation and force modeling in micro-grinding of single crystal silicon considering crystallographic effects, Int. J. Mach. Tool Manuf. 77 (2014) 1-15, https://doi.org/10.1016/j. ijmachtools.2013.10.003.

[5]J. Cheng, Y. Gong, J. Wang, Modeling and evaluating of surface roughness prediction in micro-grinding on soda-lime glass considering tool characterization, Chin. J. Mech. Eng. 26 (2013) 1091-1100, https://doi.org/10.3901/ CJME.2013.06.1091.

[6]J. Cheng, C. Wang, X. Wen, Y. Gong, Modeling and experimental study on micro- fracture behavior and restraining technology in micro-grinding of glass, Int. J. Mach. Tool Manuf. 85 (2014) 36-48, https://doi.org/10.1016/j. ijmachtools.2014.05.002.