基于GARCH-VaR 模型的投资风险评估分析——以茅台股票为例

李 银，伍晓晴，林芯怡，朱文静，杨 艳

（韶关学院 数学与统计学院，广东 韶关 512005）

股票投资的发展历史悠久，人们生活水平的逐步提高带动了股票市场的飞速发展，股份公司数量大幅增加，人们对股票投资表现活跃。然而风险在股票投资中一直存在，如何让投资者达到“投资最小，产出最大”的目的，则需要对股票风险及收益进行评估。

在金融市场中，能够度量金融投资风险的VaR 方法越来越得到国际上的关注和认可，该方法衡量风险具有速度快、高精准等特点。张锡［1］通过对上证指数实证分析，运用历史模拟法、方差-协方差方法、蒙特卡罗方法对VaR、CVaR 进行计算，发现VaR、CVaR 在评估金融风险中具有较好的度量性。赵文清等［2］从宏观、中观、微观角度分析黄山旅游板块指数，结果表明VaR 方法能使风险评估达到更高的精准性。此外，VaR 评估方法也广泛以GARCH 模型和RiskMetrics 模型为基础进行研究。林丛［3］通过EGARCH 模型和VaR 方法对泸深300 指数进行风险预测，并提出相应的投资风险评估建议。陈维龙［4］研究发现GARCH 模型对收益率拟合具有良好效果，能主要反映收益率的波动性特征，并结合VaR 方法，更好地反映了投资风险。郑凌琳［5］基于证券综合指数数据，分别建立GARCH 模型、GARCH-M模型和非对称的GARCH 模型，并结合显著性和AIC、SC 值的大小确定模型拟合的效果。Frey 建立GARCH模型分析收益率并提出精准计算VaR 评估方法。

1 模型介绍

自回归条件方差模型（autorgressive conditional heteroskedasticity mode，ARCH 模型）是恩格尔提出的，运用此模型时人们往往假设序列为正态分布，而博勒斯莱文将ARCH 拓展为GARCH 模型－广义回归条件异方差模型［6］。在金融随机序列中，真实的方差与模型预测的方差之间会存在一定的误差，扰乱项ut的条件方差依赖于它的前一项条件方差ut-1，即ARCH 模型。

无偏估计的表达式为

其中，σt为第t 天的股票波动率，σt2为第t 天的方差，股票第i 天的收益为pi，μi为对数收益率，μ 为最近m 天的对数收益率的平均值。

ARCH 模型表达式为

其中，yt为第t 天的收益率，σt2为第t 天的方差，εt为一个实值时间离散随机过程。

1.1 GARCH 模型

为了解决回归预测中估计参数数量多带来的问题，经济学家Clive Granger 创建了GARCH 模型［7］。广义自回归条件异方差模型（GARCH 模型）的主要思想是：用一个或两个σ2替代很多εt2的滞后值。这是一种回归模型，GARCH 模型的优点在于该框架下可以很好地处理金融时序的数据。

条件均值方程为

条件方差方程为

其中，ω＞0，ai＞0，βi＞0，，Rt为第t 天的对数收益率，σt2为第t 天的方差。若GARCH 模型中p=0，那么Rt则退化为服从模型MA（q）（滑动平均）过程。同理，当q=0 时，则原GARCH（p，q）退化为ARCH 模型，其实ARCH 模型是特殊的GARCH 模型的一种。

1.2 EGARCH 模型

GARCH 模型的起伏都是对称的，而且会出现杠杆效应。EGARCH 模型可以处理杠杆效应，即取消负面消息，对市场影响更大，和非对称效应、正收益和负收益对方差的影响不一样。

条件方差方程为

1.3 TGARCH 模型

TGARCH 模型正面信息的波动比负面信息小。条件方差方程为

其中，γrht-rτt-r为非对称效应项，ht-r为自变量，σt≥0 时取0，否则取1。当τt-r＜0 时，说明下跌α+γ 倍；τt＞0，说明上升α 倍。

1.4 VaR 模型

VaR 指的是在一定的置信水平下的风险价值，常用来衡量金融风险及金融资产在未来某一时间内所面临的最大损失。主要有三种计算方法：历史模拟法［8］、方差-协方差法、蒙特卡罗模拟法［9］，这三种计算方法的优缺点如表1 所示。

表1 计算VaR 的三种方法优缺点一览表

1.5 方差-协方差法

本文利用方差-协方差法（GARCH）计算风险值，GARCH 模型在金融数据描述方面应用广泛，且表现优异［7］。在实际应用中，尖峰厚尾的特征是金融时间序列常见的特征，因此可以增加在刻画尖峰厚尾特征方面表现更好的假设t 分布与GED 分布。

正态分布的概率密度函数式为

其中，μ 为均值，σ2为方差。

t 分布的概率密度函数式为

其中，Γ（*）为伽马函数，v 为自由度。

GED 分布（广义误差分布）的概率密度函数式为

其中，Γ（*）为伽马函数，v 为自由度，λ 为尾部厚度参数。

假设股票收盘价为P，收益率R 的期望值为E（R），最小收益率Ra为由Prob（R＜Ra）=1-α 得出的置信水平α 下的最小收益率。若收益率R 的期望收益为μ，标准差为σ。记P0为持有期末时股票的最小值，置信水平为α，Za为对应分位数，则Ra表示为Ra=μ-Zaσ，那么有以下公式

其中，VaR 为第t 天的风险值，置信水平为α，Za为对应分位数，Pt-1为第t-1 天的收益率。

2 实证分析

本文以茅台酒股票为例，利用方差－协方差法（GARCH 模型）计算其VaR 值。

2.1 数据收集

在我国股票市场迅速发展中，作为经典白酒贵州茅台，其股票占有一定的地位。本文通过网易财经平台选取贵州茅台作为研究对象，选取的时间段为2001 年8 月27 日至2021 年8 月6 日，如表2 所示，近20 年的数据样本能够更全面地分析股票波动情况（数据来源网址：https://money.163.com/）。

表2 贵州茅台股票相关信息

2.2 数据处理

研究发现，与金融时间相关的数据通常具有尖峰厚尾、偏态的性质，这种性质不符合正态分布的特征，不利于建立模型。因此建立模型前，需要对收集数据进行处理，本文利用式（1）计算股票的收益率，可通过算术收益率和对数收益率这两个方法实现。相比算术收益率，对数收益率在股票市场中运用范围更广，主要具有以下优势：数据经过对数处理，不仅可使数据平滑，而且能减少异方差数据带来的影响；具有收益率可加性和价格上下波动的对称性等等。因此，本文选取对数收益率方法计算该股票的日收益率，计算公式为

其中，pt-1、pt分别为第t-1 期和第t 期的收盘价。

得到的收益率利用Matlab 作出贵州茅台股票收益率的变化情况图，如图1、2 所示。

图1 收益率波动图

图2 对数收益率波动图

通过观察图1、2 的收益率变化情况，从上市到2021 年8 月贵州茅台股票收益率大部分在零界限上下波动，波动的幅度不大，绝大部分在0.05～-0.05 之间，说明收益率具有平稳性。不难发现，前期收益率的波动较小，而后期的波动率较大，体现了金融上的集聚性——收益率在平稳期变化不大，而在非平稳期变化较大。图中的第3 500～4 500 个观测值，出现了两次很大的波动，其中大幅度变化接着大幅度变化，小幅度变化接着小幅度变化，此外，在第3 000～3 500 个观测值也可观察出此现象。通过此现象，可得到金融时间序列的变化与经济现象的惯性有着较高的关联。

2.3 正态性检验

为了更直观地看出收益率的变化规律，下面利用SPSS 软件做出对数收益率的正态概率图和Q-Q图，分别如图3、4 所示，收益率的描述性统计结果如表3 所示。

表3 收益率描述性统计表

图3 正态概率直方图

统计结果显示：经过数据处理后，贵州茅台股票的对数日收益率平均值为0.000 8，标准差为0.021 2，这表明样本数据在一定程度上具有离散性。偏度系数大于0，反映了收益率分布具有右偏性，即数据样本中存在部分较大的数，也表明了样本数据具有不对称性。峰度系数为7.128，明显地大于0，则表明收益率分布相对于正态分布而言，其分布密度曲线更陡峭。综上所述，贵州茅台收益率具有“尖峰厚尾”的特征。

对于正态概率图，图4 中的直线斜率为标准差，截距为平均值，能够反映正态分布情况。可以看到大部分数据近似在该直线上下变化，表明对数收益率近似服从正态分布，而在数据左右两端与该直线存在一定的距离。

图4 正态Q-Q 图

2.4 平稳性检验

对于有关时间序列的数据需要检验其平稳性。利用Ewiewr 进行ADF 检验的步骤为：

（1）对原始数据进行检验，如果拒绝原假设，说明原始时间序列不平稳；

（2）再对原始数据的差分进行检验，若检验还是没有通过，则需要对原数据二阶差分检验。若不存在单位根，即P 值小于0.05，接受原假设，说明该数据为平稳序列。ADF 单位根检验结果（如图5 所示）显示，P 值都显著小于0.05，则表明拒绝原假设——序列服从随机游走，即对数收益率序列是平稳序列，不含单位根。

图5 平稳性检验结果

2.5 自相关性检验

如果收益率中存在自相关性，就会对模型建立的正确性产生一定的影响，为了寻找更好的拟合模型，检验序列的自相关性，本文利用SPSS25.0 做出贵州茅台的收益序列的自相关图，结果如图6 所示。

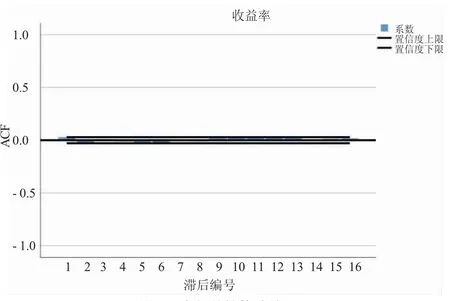
图6 自相关性检验结果

结果显示，贵州茅台对数收益率的自相关系数绝大部分落入一倍标准差范围内，因此可认为序列不存在自相关性，在后续所要建立的GARCH 模型中不需要加上自相关的描述部分。

2.6 异方差检验

对所建立的方程GARCH（1，1）进行异方差的ARCH-LM检验，检查是否存在异方差，得到的残差序列检验结果如表4 所示。

表4 残差序列检验结果

发现此模型显著水平为5%以下，P 值为0.997 2＞0.05，滞后阶数10 阶时接受原假设，则可认为序列残差值不存在ARCH 效应。

3 模型的建立

在前面部分，通过对数收益率波动图得到金融界上的集聚性，因此对于存在波动急剧的时间序列，本文选用GARCH 模型进行预测风险值VaR，它能够更好地避免高阶移动平均阶数对结果拟合精确度带来的影响，且描述金融上的集聚性［10］。

为了确定模型以及模型中的参数，在建立模型前需要对参数取值进行多次拟合，以得到拟合效果尚好的模型。判断拟合效果的方法为AIC 准则，即AIC 的值越小，拟合效果越好。为了弥补AIC 准则的不足之处——AIC 准则拟合效果会受到数据量大小的影响，本文通过AIC（赤池信息准则）、BIC（贝叶斯信息准则）最小准则来确定GARCH 模型中的参数取值，AIC 和BIC 的平均值越小，模型拟合的效果越好。

本文分别计算GARCH（1，1）、GARCH（2，1）、GARCH（1，2）、GARCH（2，2）、EGARCH（1，1）、EGARCH（1，2）、EGARCH（2，1）、TARCH（1，1）、TARCH（1，2）、TARCH（2，1）模型的AIC 和BIC 值，结果如表5 所示。

表5 模型拟合结果

由表5 可知，建立了GARCH（1，2）的P 值为0.088 5＞0.05，系数不相关，EGARCH（1，2）后发现其P 值为0.976 0＞0.05，系数不相关，TARCH（1，1）的P 值为0.907 7＞0.05，TARCH（1，2）的P 值为0.349 7＞0.05，系数不相关，而GARCH（1，1）模型的AIC 和BIC 平均值最小，其P 值为0.031 6＜0.05，系数高度相关，GARCH（2，2）的P 值0.0307＜0.05,模型拟合出的系数高度相关。因此，下文基于GARCH（1，1）和GARCH（2，2）分别计算茅台股票风险值（VaR）。

3.1 GARCH（1，1）模型求解

本文通过Ewiewr 软件拟合GARCH（1，1）模型，所得结果如图7 所示。其中，Rt为第t 天的对数收益率，σt2为第t 天的方差。

图7 GARCH（1，1）拟合结果

从估计结果可以看出，所建立的GARCH（1，1）模型中，α+β 之和为0.872 709，小于1，因此GARCH（1，1）过程是平稳的，条件方差ARCH 和GARCH 项都属于高度显著的，因此，收益率序列具有明显的波动集簇性。

3.2 GARCH（2，2）模型求解

为了达到结果的准确性以及进行模型结果的比较，本文建立GARCH（2，2）模型并进行求解，结果如图8 所示。

图8 GARCH（2，2）拟合结果

其中，Rt为第t 天的对数收益率，σt2为第t 天的方差。

从估计结果可以看出，所建立的GARCH（2，2）模型中，α+β 之和小于1，则GARCH（2，2）过程是平稳的，条件方差ARCH 和GARCH 项都属于高度显著的，因此收益率序列具有明显的波动集簇性。

利用EViews 8.0 中的Forest 和已经建立的GARCH（1，1）、GARCH（2，2），可以预测出第t 天的条件方差σ2。

4 VaR 的计算

基于上述建立的模型计算出方差的预测值，结合Matlab 计算第t 天的风险值。对处理好的数据计算VaR 和实际损失，损失值的计算为前一天的收盘价减去后一天的收盘价，即Pt-1-Pt。本文采用的计算方法是基于GARCH 模型计算的VaR 值，由式（12）VaR=Pt-1Zασt，其中，Pt-1是t-1 天的股票收盘价，Zα为置信水平下分位数，显著性水平为95%，计算得到Zα=1.644 64，σt是收益率的标准差，部分结果如表6、7 所示。

表6 GARCH（1，1）计算出的部分风险值

表7 GARCH（2，2）计算出的部分风险值

4.1 模型的稳健性分析

对GARCH（1，1）计算得到的VaR 值进行稳健性检验，以损失值超出VaR 值的天数为失败天数，利用Matlab 计算失败率，总天数为4 734 天，失败天数为132 天，失败率为2.79%，接近显著性水平。模型对收益率时间序列的分布特征拟合程度较好，结果如图9 所示。

图9 GARCH（1，1）稳健性检验图

对GARCH（2，2）计算得到的VaR 值进行稳健性检验，以损失值超出VaR 值的天数为失败天数，利用Matlab 计算失败率，总天数为4 737 天，失败天数为133 天，失败率为2.81%，通过稳健性检验，如图10所示。

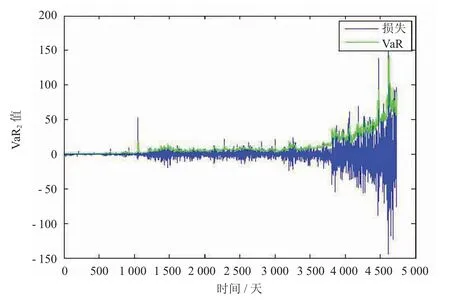
图10 GARCH（1，1）稳健性检验图

4.2 风险值VaR 的Kupiec 检验

在利用GARCH 模型计算得到VaR 的值后，需要对其预测风险的准确性进行检验，本文采用简单有效的Kupiec 失败率检验法进行检验。将VaR 与对应的损失值比较，当真实亏损大于预估VaR 值时记为失败，实际损失的计算公式为Pt-1-Pt。在给定显著性水平α 时，实际检验天数为N，失败天数为x，失败率为p=x/N，期望失败概率为1-α。在原假设的条件下，引入如下LR 统计量

当原假设为真，LR～χ2（1）。若LR 的值在置信区间内，则说明模型预测结果较准确；若LR 值在置信区间左边区域，则说明预测损失高于实际损失，LR 值在置信区间右边，则说明预测损失低于实际损失。

基于Matlab 软件，对计算的VaR值进行Kupiec 检验。χ2（1）在显著性水平α=0.975 和α=0.025 的置信区间为［0.001，5.024］，根据上述稳健性检验的结果，对于GARCH（1，1）模型计算的VaR 值，实际检验天数N=4 734，失败天数x=132，失败率p=0.027 9，显著性水平α=0.025，期望失败概率1-α。计算得到LR1=1.557 4，接受原假设，预测结果准确度较高。CARCH（2，2）模型计算的VaR值，实际检验天数N=4 737，失败天数x=133，失败率p=0.028 1，显著性水平α=0.025，期望失败概率1-α。计算得到LR2=1.789 5，接受原假设，预测结果准确度较高。

5 结语

基于国内外已有的模型研究成果，本文研究了基于GARCH 类模型计算茅台股票的VaR风险值。首先，通过预测未来茅台股票价格的变化趋势以及评估潜在的投资损失，进而判断茅台股票何时风险最小，以达到“高利润低风险”目的。在95%的置信水平下所建立的GARCH（1，1）-VaR 模型失败率为2.79%和GARCH（2，2）-VaR 模型失败率为2.81%。实证分析结果表明，GARCH 类模型更优于解决对称的序列。此外，投资者在选择投资组合时，可以仅简单地通过所预测出的风险值概括整个组合的潜在风险。此模型适用于不同的股票收益序列，运用GARCH-VaR 模型在一定程度上可以提前预测茅台股票价格的波动范围，评估可能的投资损失，从而可以更好地掌握股票的走势，即何时风险最小，有利于提高利润回报。