基于圆孔的光近场远场衍射实验研究

袁宇博，赵小侠，郭 钊，杨 迪，王 浩，罗奇松，贺俊芳，王碧熙，王红英，付福兴，杨森林

(西安文理学院 机械与材料工程学院，陕西 西安 710065)

圆孔衍射根据光源与圆孔以及圆孔与衍射屏之间的距离远近可以分为：菲涅尔圆孔衍射(近场衍射)和夫琅禾费圆孔衍射(远场衍射)。夫琅禾费圆孔衍射轴线上的光强可以根据惠更斯-菲涅尔原理积分得到，而菲涅尔圆孔衍射光强分布，原理上也可以从惠更斯-菲涅尔原理出发计算得到。但是在实际情况下，由于光源与障碍物圆孔以及与衍射屏的距离关系会导致光强计算相当复杂。菲涅尔圆孔衍射的传统理论是建立在菲涅尔的半波带法对圆孔衍射的定性解释。孙景亭[1-4]曾在球面波入射的情况下,导出了菲涅尔圆孔衍射时轴上光强分布的解析表达式,并对轴上光强分布进行了定量分析讨论；用标量衍射理论导出了平行光入射时，圆孔衍射的精确积分表达式；用数值积分法可求出整个衍射空间光场和光强的分布；也导出了普遍情况下的菲涅尔圆孔衍射的精确积分表达式和非傍轴区轴上点的菲涅尔圆孔衍射的解析表达式，并借助于数值计算方法，模拟出衍射光强随各种不同参数而变化的曲线。曹国荣[5]曾采用振幅矢量法，找出了菲涅尔圆孔衍射轴线上光强分布的规律及解析表达式。相对于孙景亭老师的推导理论，振幅矢量图法研究菲涅尔圆孔衍射轴线上的光强分布规律，具有简单的特点，又比菲涅耳半波带法优越，在一定的近似条件下可以得到与孙老师理论相同的结果。但是结果不够形象。于建强[6]在远场傍轴条件下，推导了圆孔夫琅禾费衍射场三维分布的积分表达式，并基于Matlab软件进行了数值积分，得到了圆孔夫琅禾费衍射图样的三维光强分布数据。游开明[7]利用Hankel变换算法，克服菲涅耳衍射积分计算的复杂性和因光波频率高而导致的采样点数目巨大两大难题，将二维计算变换为一维计算，并利用球面波因子处理，在普通PC上实现了菲涅耳圆孔衍射的计算机模拟演示。两位老师的模拟研究相对理论推导形象，但没有实际的实验结果形象生动。

项目主要搭建了圆孔的菲涅尔衍射实验，研究了在保持光源与衍射物圆孔距离不变的条件下，改变衍射屏与障碍物的距离，观察衍射屏上衍射光强的变化。从而与圆孔夫琅禾费衍射实验比较，得出可以把圆孔夫琅禾费衍射看作菲涅尔圆孔衍射的一个特例的结论。这与苏海涛[8]的点光源在聚焦条件下的菲涅尔圆孔衍射，当光源与目标物的距离增大时，衍射光强(图样)就会发生改变，从而使菲涅尔圆孔衍射过渡到夫琅禾费圆孔衍射的结论是一致的。

1 理论分析

1.在菲涅尔圆孔衍射中，根据惠更斯原理，当光源与半径恒定的衍射物圆孔和圆孔与观察屏之间的距离保持不变，对于菲涅尔圆孔衍射引用半波带划分法，得到菲涅尔圆孔对称轴上一点处的衍射图样的规律[9]：

通过圆孔的波面划分为k个半波带，当k为奇数时，观察屏中央衍射图样为亮斑，当k为偶数时，观察屏中央衍射图样为暗斑[10，11]。

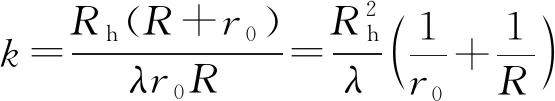
(1)

上式1中Rh为圆孔半径，R为点光源到圆孔的球面波的半径，r0为点光源到圆孔的球面波与通过圆孔的对称轴的交点到对称轴上观察点之间的距离，λ为单色光的波长。

由式1可以得出，当光源给定，圆孔的大小即圆孔半径Rh恒定，并且光源与圆孔之间的距离恒定即光源到圆孔的球面波半径R恒定情况下，在圆孔对称轴上的观察点位置改变，即r0值发生变化，划分的半波带个数k也随之改变。从而使观察点处的衍射图样发生亮暗的周期性变化。

2.苏海涛通过数学推导的方法[8]，讨论聚焦条件下菲涅尔圆孔衍射，推出夫琅禾费圆孔衍射合振动的函数式即光强分布如下。

菲涅尔圆孔衍射合振动函数式：

y=H0cos[wt-ks(θ)-kq0φ0sinθ]

(2)

式中H0为贝塞尔函数，

夫琅禾费圆孔衍射相当于光源距离很远时发生菲涅尔圆孔衍射，满足2φ0→0，此时q0φ0=r(r为衍射圆孔半径)，得到下式3夫琅禾费圆孔衍射合振动函数式：

y=H0cos[wt-ks(θ)-krsinθ]

(3)

苏老师理论分析了菲涅尔圆孔衍射过渡到夫琅禾费圆孔衍射，即可以把夫琅禾费圆孔衍射看成菲涅尔圆孔衍射的一个特例。

项目研究在保持光源与衍射物圆孔距离不变的条件下，改变观察屏与障碍物的距离，观察观察屏上衍射光强的变化。从而与圆孔夫琅禾费衍射实验相比较，也得出可以把圆孔夫琅禾费衍射看作菲涅尔圆孔衍射的一个特例的结论。

2 实验装置

实验室中搭建的近场菲涅尔圆孔衍射实验装置图如下图1所示。

图1 实验室搭建的菲涅尔衍射实验装置图

图1中从右向左依次为：1-实验光源532 nm激光器；2-圆形可调衰减器；3-空间光滤波器；4-聚焦为准直透镜(Φ25.4,f100.0)；5-聚焦透镜(Φ40,f150.0)；6-衍射物-圆孔；7-CCD数字相机(通过数据线与电脑连接进行图像的观察)。

实验中依次调整激光器、空间滤波器和准直镜；安装聚焦透镜和衍射物-圆孔和CCD数字相机。搭建好如上图1的近场菲涅尔圆孔衍射光路后，让光源照射在衍射物圆孔上，通过软件适当调节数字摄像机CCD的成像参数，并通过数据线把采集到的衍射图样传输到电脑中进行观察。实验中选择直径250 μm的圆孔为衍射物来进行实验验证的。

3 实验结果

实验过程中，保持光路中的其他光学器件不变，仅改变衍射物圆孔和相机之间的距离，实验采集到的圆孔衍射图样如下。

(1)衍射物圆孔与相机之间距离为60.0 mm时得到的菲涅尔衍射图如下图2所示。

图2 衍射物距CCD相机60.0 mm处的菲涅尔衍射图样

图2中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为亮斑，根据半波带理论，当CCD相机到圆孔之间的距离为60.0 mm情况下，可以把光源到圆孔的波面划分为奇数个半波带。

(2)衍射物圆孔与相机之间距离为103.0 mm时得到的菲涅尔衍射图如下图3所示。

图3 衍射物距CCD相机103.0 mm处的菲涅尔衍射图样

图3中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为暗斑，根据半波带理论，当CCD相机到圆孔之间的距离为103.0 mm情况下，可以把光源到圆孔的波面划分为偶数个半波带。

(3)衍射物圆孔与相机之间距离为168.0 mm时得到的菲涅尔衍射图如下图4所示。

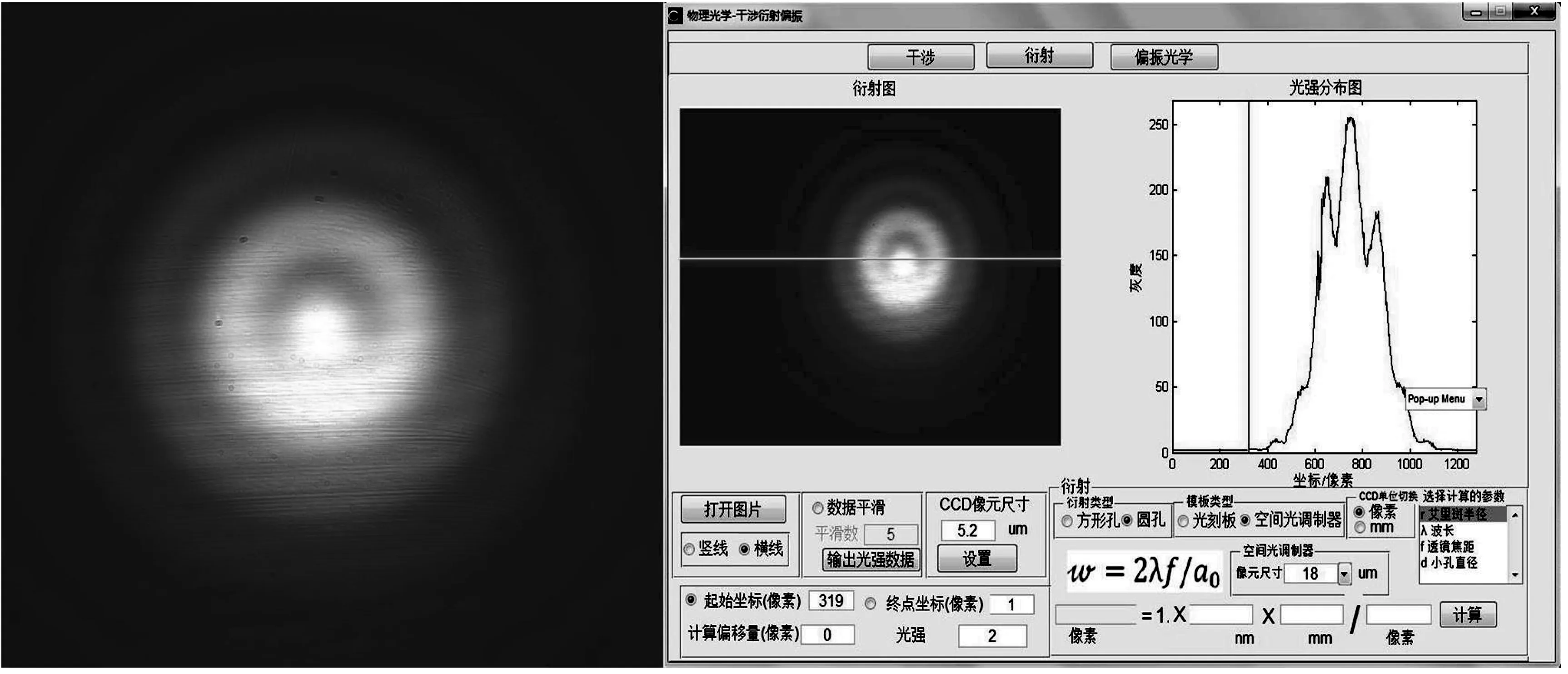
图4 衍射物距CCD相机168.0 mm处的菲涅尔衍射图样

图4中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为亮斑边缘有暗环亮环分布，根据半波带理论，当CCD相机到圆孔之间的距离为168.0 mm情况下，光源到圆孔的波面划分的半波带个数正在由偶数向奇数变化，不是整数而是小数。

(4)衍射物圆孔与相机之间距离为224.0 mm时得到的菲涅尔衍射图如下图5所示。

图5 衍射物距CCD相机224.0 mm处的菲涅尔衍射图样

图5中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为暗斑，根据半波带理论，当CCD相机到圆孔之间的距离为224.0 mm情况下，可以把光源到圆孔的波面划分为偶数个半波带。

(5)衍射物圆孔与相机之间距离为364.0 mm时得到的菲涅尔衍射图如下图6所示。

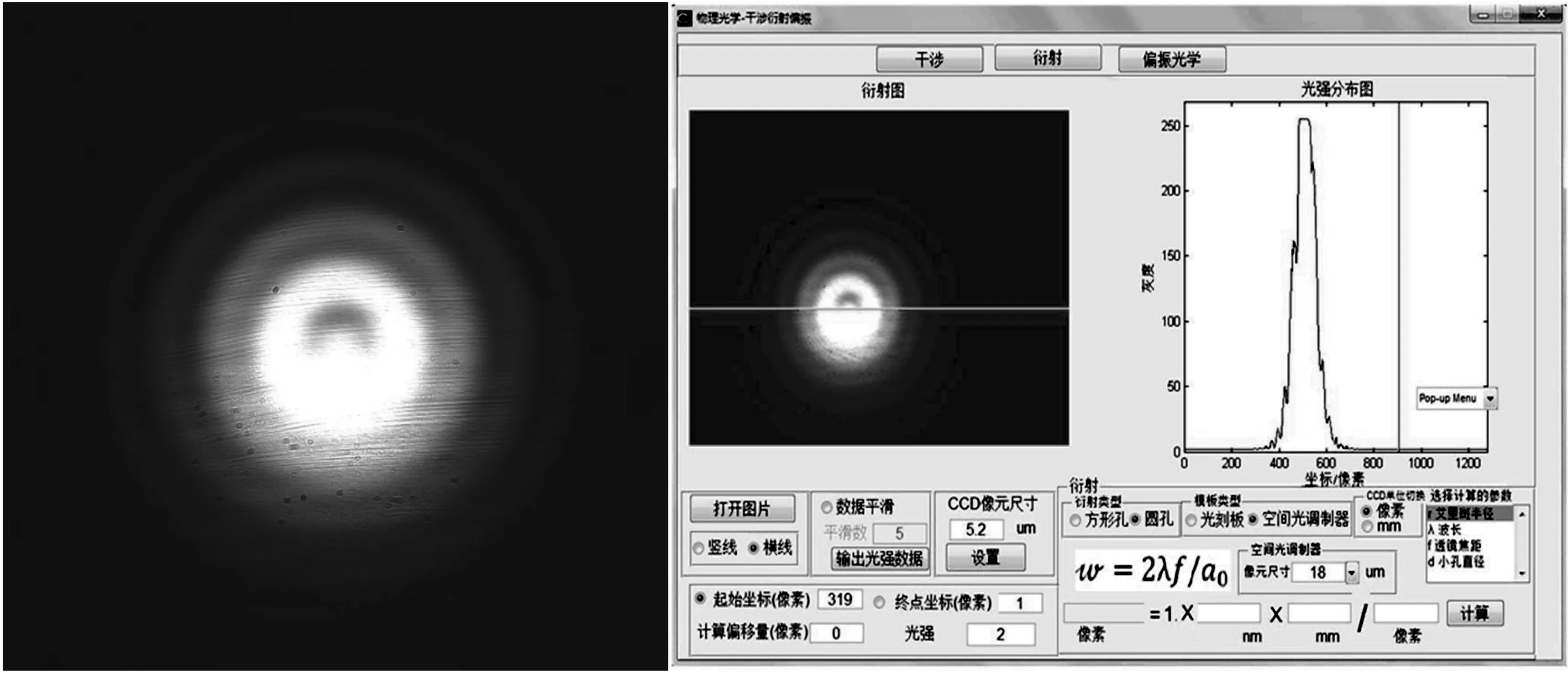
图6 衍射物距CCD相机364.0 mm处的菲涅尔圆孔衍射图样

图6中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为亮斑边缘有亮环和暗环的分布，根据半波带理论，当CCD相机到圆孔之间的距离为364.0 mm情况下，光源到圆孔的波面划分的半波带个数正在由偶数向奇数变化，也非整数而是小数，但是该数字已经非常接近于某一奇数。

(6)衍射物圆孔与相机之间距离为402.0 mm时得到的菲涅尔衍射图如下图7所示。

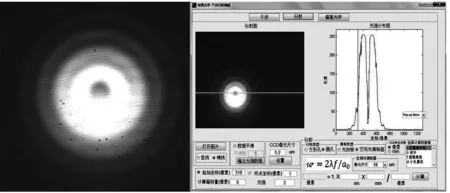
图7 衍射物距CCD相机402.0 mm处的菲涅尔圆孔衍射图样

图7中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为暗斑边缘有亮环和暗环的分布，根据半波带理论，当CCD相机到圆孔之间的距离为402.0 mm情况下，光源到圆孔的波面划分的半波带个数正在由奇数向偶数变化，也非整数而是小数，但是该数字已经非常接近于某一偶数。

(7)衍射物圆孔与相机之间距离为620.0 mm时得到的菲涅尔衍射图如下图8所示。

图8 衍射物距CCD相机620.0 mm处的菲涅尔圆孔衍射图样

图8中左图为圆孔菲涅尔衍射光斑，右图为圆孔菲涅尔衍射图样的光强分布。衍射图样中心为亮斑，根据半波带理论，当CCD相机到圆孔之间的距离为620.0 mm情况下，光源到圆孔的波面划分为奇数个半波带。

实验室中搭建的夫琅禾费衍射实验装置图如下图9所示。

图9 实验室搭建的夫琅禾费衍射实验装置图

图9中从右向左依次为：1-实验光源：532 nm激光器；2-圆形可调衰减器；3-空间光滤波器；4-准直透镜(Φ25.4,f100.0)；5-聚焦透镜(Φ40,f150.0)；6-衍射物-圆孔；7-聚焦透镜(Φ40,f150.0)；8-CCD数字相机(通过数据线与电脑连接)。实验得到的夫琅禾费衍射图样如下图10所示。

图10夫琅禾费远场衍射的图样与图10的菲涅尔衍射图样进行对比发现：当目标物与光源距离足够大时，就发生远场衍射，从而使近场衍射过渡到远场衍射。从图10可以清楚地看到，当目标物与光源的距离增大时，划分的半波带个数为k，根据k的奇偶性使衍射图样发生变化。当目标物与光源的距离足够大时，近场衍射就过渡到远场衍射。通过实验可以更加深入的理解近远场衍射的实质。

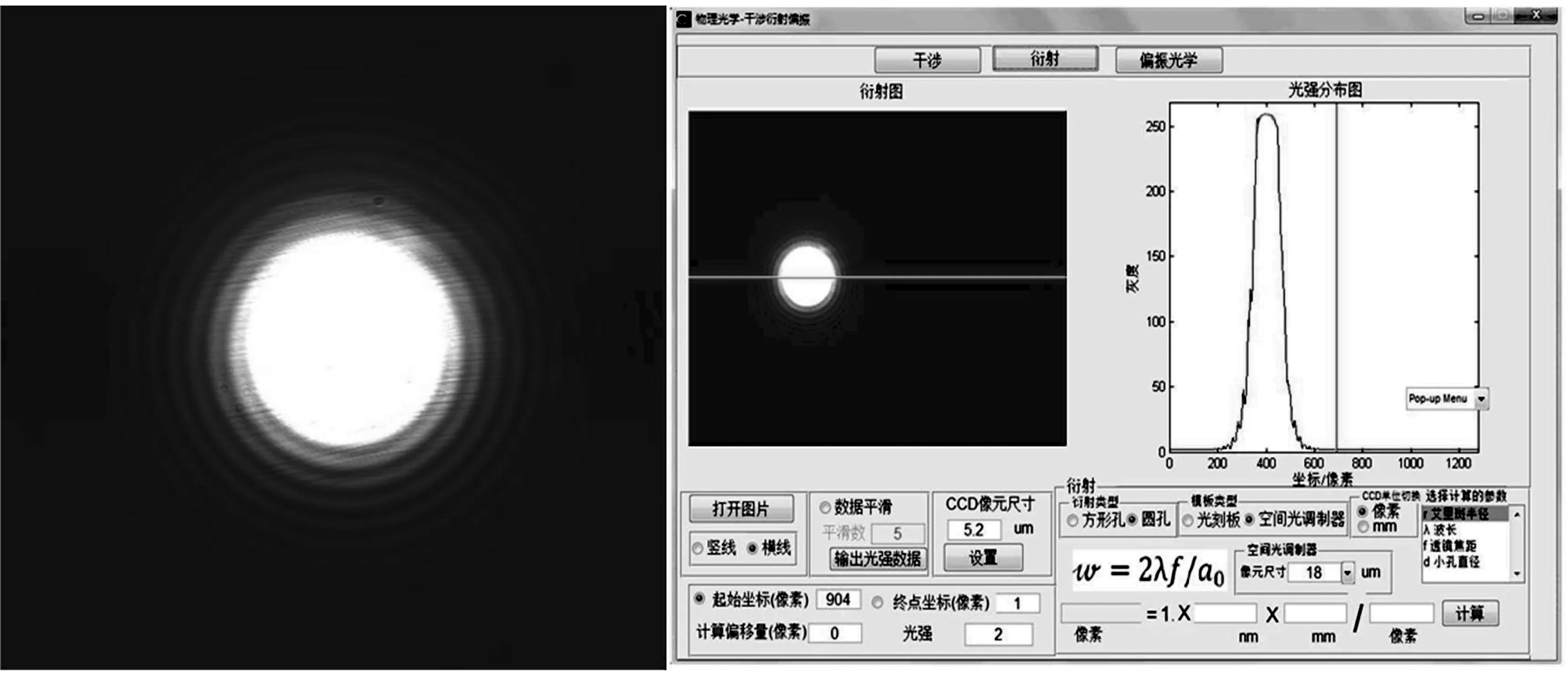
图10 夫琅禾费衍射图(左边为衍射图样右边为光强分析)

4 结 语

基于圆孔菲涅尔衍射原理，搭建了菲涅尔衍射和夫琅禾费衍射两个实验光路。在保持光源到衍射物距离不变的情况下，通过改变衍射物到观察屏的距离，在观察屏上得到了周期性变化的衍射图样，当衍射物与观察屏之间距离足够大时最终将近场衍射过渡到远场衍射。实验证实了夫琅禾费圆孔衍射可以看作菲涅尔圆孔衍射的一个特例的结论。这与苏海涛[8]的点光源在聚焦条件下的菲涅尔圆孔衍射，当光源与目标物的距离增大时菲涅尔圆孔衍射过渡到夫琅禾费圆孔衍射的结论相一致。加深了对圆孔的菲涅尔衍射和夫琅禾费衍射的理解，弄清楚了两种衍射之间的相互关系。