基于1stOpt的团簇优化实验程序设计探索

梁雪梅，黄吴夕，冯子俨,陈恒杰

(重庆科技学院 数理与大数据学院，重庆 401331)

团簇是物质从微观到宏观的过渡状态，是物质存在的重要形式之一。分子团簇的结构对其性质有着重要的影响，因此，对分子团簇研究的首要任务为确定其结构。然而，现有的实验很难分离得到不同尺度的团簇，对团簇结构的测定则更加困难，特别是当团簇尺度较大时，这项任务变的几乎不可能。因此，在团簇结构的研究方面往往需要结合理论计算帮助获得团簇的结构[1,2]。目前针对团簇结构主要有两个研究方向：一、利用基于量子力学的各类从头计算软件得到团簇在某一结构下的单点能，利用有偏或无偏优化算法来更新结构，通过多次迭代得到最低能结构，限于当前计算机资源的限制，这种方式也仅在中小尺度的团簇下适用，对中大尺度团簇，由于耗费的计算资源巨量而很难开展。二、利用实验或基于准确的量子理论计算下的团簇特性，构造出一个合理的势能函数，然后用该势能函数结合各类优化算法对包括中大尺度在内的分子团簇结构进行计算或预测[3-5]，其数学本质为一能量最小化的最优化问题。两种方法都需要研究者相当熟悉相应的优化算法，强大的编程能力，因此学习曲线相对较长[6-8]。

1stOpt被认为是当前全世界最好的全局优化程序[9]，其强大的通用/稳健全局优化算法(UGO)，接近数学描述且简单的编程语言和灵活多变的编程方式。我们想能不能通过二次开发，利用1stOpt的优化功能，在团簇优化时基于该软件进行结构更新，这样研究者可节约大量研究算法本身及其算法编写的时间和精力，使其能更多地关注到团簇问题本身。同时也可以通过该问题地解决来测试1stOpt的优化能力，给我们解决其他问题奠定基础。

1 实验原理

1.1 势函数

本文共测试了三种势函数，rij表示各原子间距，本质是对角线为零的对称方阵，为自变量。ULJ，UG和USC分别表示函数的势能，为因变量，N为构成团簇的原子总数，三种函数的具体形式如下[10,11]：

Lennard-Jones势：

(1)

Gupta势：

(2)

(3)

Sutton-Chen势：

(4)

(5)

1.2 设计思路

图1为程序设计思想及流程图，其中结构更新由1stOpt黑箱实现，是团簇优化中寻找最低能结构的核心问题，也是1stOpt的优势所在。收敛判断部分由1stOpt的图形界面设定，其余由1stOpt结合内嵌语言或动态库编程实现。原则上自变量可选择笛卡尔坐标(xyz)，分子间距(rij)或分子内坐标(键长，键角，二面角等)，为了计算的便利，本文选择xyz型坐标，可通过简单处理或借助于量化工具即可得到分子间距或分子内坐标。由于分子是可平移，旋转的，所以优化的xyz坐标不唯一，但与之对应的分子间距、内坐标和最低能是唯一的。

图1 程序流程图

2 结果与分析

结合1stOpt编程，分别用内嵌程序语言(如Pascal，Fortran等)以及调用外部编译器编写和编译的动态库(dll)，实现了上述三种势函数的单原子分子团簇结构优化程序，探索了双原子合金团簇结构优化程序，计算中采用全局优化算法或稳健全局优化算法，自动选择，根据团簇尺度大小，依次选择并行数100～1 000，比率0.3～0.5,控制数30～50,收敛判断迭代50,变异率0.3～0.50。为了检验编写程序的正确性，本文所有工作同时用ABCluster软件进行了计算。

2.1 原子团簇

2.1.1 Gupta势

计算时，取参数A=0.006 946 731,ξ=0.437 81,d=3.5,p=24.943 17,q=0.292 646。表1为基于Gupta势函数，结合内嵌Pascal语言编写的1stOpt程序，用户只需改变其中的原子个数num，执行程序后便可获得相应尺度团簇中每个原子的xyz坐标和最低能量。基于该程序，我们测试了num=2～20时的团簇，结果见表2，可以看出，本文完美地再现了Darby利用遗传算法[12]和王全武等利用人工蜂群算法[13]得到的结果，说明利用1stOpt编程实现团簇结构优化是可行的，同时也验证了当前程序是可靠的。编写该程序时，研究者并不需要任何优化算法理论知识，也不需要将优化算法转化为程序的经验，只需简单了解团簇问题涉及的势函数，简单学习1stOpt编程即可完成以往需要研究者花费大量时间，前期研究算法，后期大量编程才能完成的工作，将大大降低该研究问题的知识储备和门槛。

表1 Gupta势函数计算程序

表2 Gupta势函数结果

2.1.2 Sutton-Chen势

为进一步说明程序的可靠性，我们也针对文献中经常使用的Sutton-Chen势函数进行编写，计算时取参数ε=1，c=39.432，a=1.0，n=9，m=6，程序见表3，计算结果见表4。

表3 Sutton-Chen势函数计算程序

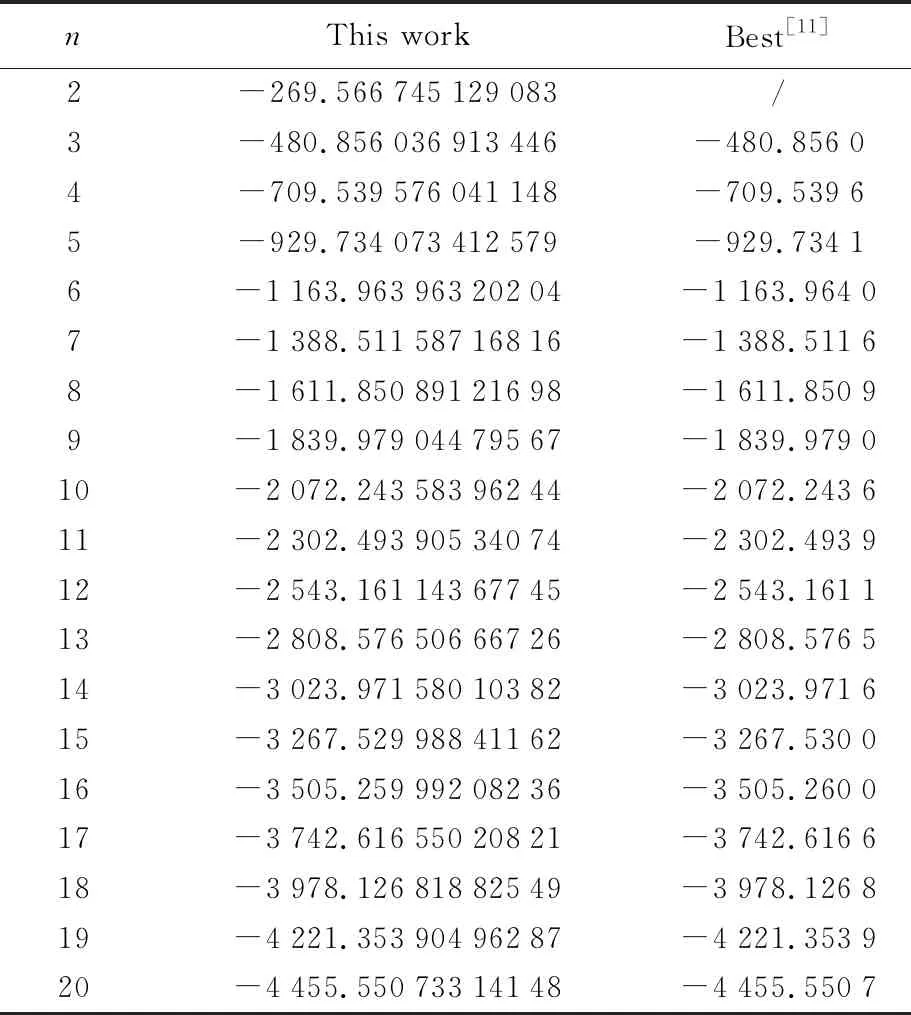
表4 Sutton-Chen势函数结果

为了比较各团簇优化算法的有效性，剑桥大学的Doye等搜集了多种势函数下已出版的最低能结构和最低能量值，本文后续均标记为Best。Doye没有给出n=2时的能量，我们优化的结果为-269.566 745 129 083，另外，同Gupta函数结果一样，在不考虑精度的前提下，当前获得的最优结果与Doye给出的最低能完全一致，再次检验了1stOpt优化原子团簇的可行性与可靠性。

2.1.3 LJ势

在一些情况下，若研究者手上已有计算势函数的子程序，或熟悉的其他计算机语言非内嵌在1stOpt中，且研究者也并不想过多的学习其他内嵌语言。这时，应用熟悉的计算机程序语言编写子程序并编译成动态库，再利用1stOpt调用该动态库则显得非常合适，这样能大大缩短程序开发周期，节约研究时间。表5展示了用Compaq Visual Fortran编写的基于LJ势函数的动态库源文件，接着，在Windows操作系统下，打开cmd窗口，并cd到存放该源文件的当前目录，用命令DF.exe/all“lj.f90”进行编译，之后将生成lj.dll文件及其他几个支撑文件，再用表6所示的1stOpt程序调用lj.dll，由于所有文件都在当前路径的同一个文件夹下，1stOpt程序调用时没有采用绝对路径。

为便于比较，LJ中的参数采用ε=1，σ=1，计算结果见表7。可见，利用1stOpt调用动态库结果和ABCluster计算的结果完全匹配，也与Doye给出的最优结果一致，不仅实践了动态库源程序的编写，编译和调用，也进一步检验了1stOpt优化团簇结构的可行性。

表5 LJ势函数下的动态库源程序

表6 1stOpt调用动态库

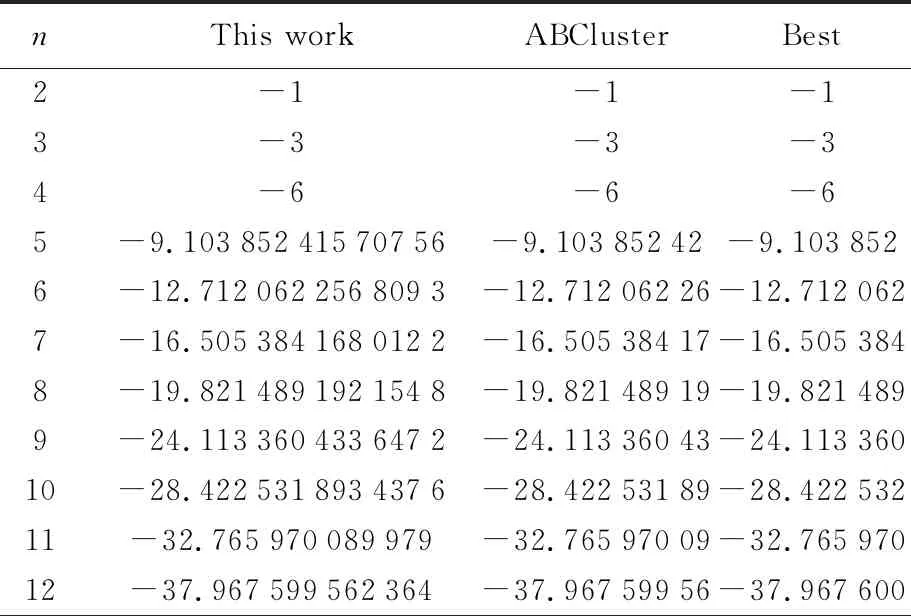
表7 Lennard-Jones势函数结果

续表

2.2 二元合金团簇

原子团簇是最简单的团簇形式，而很多情况下，团簇可能由多种原子组合而成，或者大量的几种原子加少量某种原子掺杂而成，如AgXCuy，AgXCuyAuz等。接着我们以二元合金AgXCuy团簇为例，探索了1stOpt在解决复杂团簇结构方面的可行性，程序见表8，计算结果见表9。毫无意外，1stOpt完全重复了ABCluster结果，两者完美的自洽，基于我们对ABCluster计算的经验和单原子分子团簇计算结果的比较，有理由相信两种计算结果得到的都是最低能。

表8 二元合金团簇计算程序

续表

表9 二元合金团簇AgXCuy能量优化结果

3 结 语

基于三种常见的势能函数，结合1stOpt及其内嵌的程序语言和外部调用动态库，多种程序，多种手段，初步探索了1stOpt在优化团簇结构方面的可行性，与Doye搜集的最优结果和专业团簇优化程序ABCluster计算结果比较，我们发现基于1stOpt的程序完全能够重现上述结果，因此利用1stOpt优化团簇结构是可行的。同时在执行过程中也发现了一些不足。在原子数目较少时，基于通用/稳健全局优化算法的1stOpt效率非常高，很多情况下一次或者几次迭代就能找到最低能，然而，当n增大即变量增多时，尽管最终也能找到最低能，但效率会大打折扣，有时还会陷入局部最优，我们猜测可能与以下几方面有关：一、我们的探索目前仅在停留在利用1stOpt实现团簇优化功能的可行性，因此编写的程序未进行任何优化和通用化；二、1stOpt目前仅支持Windows操作系统，而ABCluster计算是在Linux服务器上完成，两种操作系统在效率上天然的优劣，是造成效率差异的最最重要原因之一；三、ABCluster专门为团簇优化设计，为有偏算法，具有加速功能，而1stOpt为通用的优化程序，具有无偏性，因此在处理该类特定问题时效率没能大幅提升。基于上述问题，提出几点展望：首先可通过文本等操作、对自编的程序进行优化，解决同一问题尽量减少变量的同时，使得程序通用化(如多元合金不需要再写更复杂的程序，仅给出原子种类和相互间参数即可)；其次，通过动态库/内嵌语言，参数设置等实现有偏操作，缩小搜索区间，减少优化时间，提高优化效率；最后，也是研究者不可控的一点，期望七维高科开发出基于Linux操作系统的版本，开发出更加灵活的动态库接口。