诊断铁路接触网硬点CEEMDAN-SPWVD边际指数方法

2022-06-01丁宇鸣刘金朝徐晓迪张文轩杨志鹏

铁道学报 2022年5期

丁宇鸣，刘金朝，徐晓迪，张文轩，杨志鹏，王婧

(中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081)

在接触网系统中，接触线底面不平顺或接触线铅垂弹性突变的点称为硬点[1]。硬点病害的类型主要分为接触线硬弯、各种零部件或其线夹状态异常、绝缘器状态异常、锚段关节过渡不平滑以及刚性接触网状态异常这几种。而长期的硬点也会导致接触线的弯曲应力增大，造成接触线异常磨损、疲劳甚至断裂，严重时，会影响运营车辆的供电，甚至会影响车辆运行的安全性，因此对接触网状态进行分析至关重要。

接触网状态分析需要对弓网动态响应检测数据进行特征分析。对于检测信号，相关科研人员通常对其进行时域、频域、时频特征以及统计学特征分析。文献[2]即为对时域信号进行统计分析制定的接触网质量评价标准。

频域分析方法能将时域信号转换到频域，找出一个信号在不同频率下的信息(如振幅、功率、强度或相位等)。傅里叶变换即是最为常见的一种频域分析方法[3]。1995年，藤井保和等[4]使用功率谱分析了日本新干线接触线的波状磨耗及其与弓网离线的关系。2000年，张卫华等[5]提出了接触线表面不平顺的概念，并对简单形式波形的不平顺进行了分析。文献[6-8]通过分析接触力的功率谱评估接触线的不平顺状态。现代谱估计方法是以随机过程的参数模型为基础，可以提供比周期图高得多的频率分辨率，是一种高分辨率的谱估计方法[9]。因此，有相关科研人员采用现代谱估计方法中的自回归AR模型方法分析信号数据。文献[10-12]采用AR模型对弓网耦合动态特性进行分析评估。2018年，尹伊等[13]提出AR谱模型与模糊分析相结合的方法。但是，频域分析无法提取信号随时间或空间变化的频率特征。如果是非平稳信号，则频率分析方法无法完全反映信号频率变化的特征。

时频分析方法能够有效地提取数字信号各频率成分随时间空间变化的特性。WVD在单分量信号的时频特征提取中取得了良好的效果，具有最好的时频聚集性，然而由于是典型的二次型变换，在多分量信号的时频分析中会存在交叉干扰项。文献[14]通过试验确定了适用于分析高速铁路弓网接触压力信号的基于WVD分布改进的时频分布Zhao-Atlas-Mark分布(Zhao-Atlas-Mark Distribution，ZAMD)。

自适应分解时频分析以经验模态分解(Empirical Mode Decomposition，EMD)[15]方法为代表，但EMD存在模态混叠的问题。为了解决这个问题，文献[16]提出了整合经验模态分解法(Ensemble Empirical Mode Decomposition, EEMD)。文献[17-18]结合EEMD和其他方法实现接触网与受电弓结构的故障诊断。文献[19]提出了结合EEMD和WVD的方法分析受电弓垂向加速度信号，得到了接触网短波病害的时频特征。但EEMD仍然存在重建之后白噪声无法完全抵消，加和之后噪声过大的问题。为了解决EEMD这些缺陷，文献[20]提出互补集合经验模态分解法(Complementary Ensemble Empirical Mode Decomposition，CEEMD)。文献[21-22]利用CEEMD分解接触力以诊断接触网结构状态。但在CEEMD分解中信号加上不同的白噪声可能会产生不同数量的模函数，模函数集总平均的问题仍未解决。文献[23]提出了改进的CEEMDAN。

在加速度诊断接触网故障方面，部分科研人员利用原始信号的幅值直接进行判断。文献[24-25]均是通过判断加速度原始信号的幅值是否超出阈值来检测硬点。更多的科研人员则是对原始数据进行一系列分析计算后再对故障进行诊断。文献[26]提出了一种基于支持向量机和受电弓振动响应的接触网故障识别方法。文献[19]通过计算信号的移动有效值，再进行归一化得到接触网冲击指数以实现硬点诊断。文献[27]利用四元数理论去除误差，以获取的振动加速度数据为基础，应用带滤波的离散频域积分方法求解接触线振动位移，判断受电弓当前的运行状态。文献[28]提出结合EEMD和三种熵建立模型，实现基于垂直加速度和水平加速度信号的吊弦断裂检测方法。然而，上述研究均未对从检测数据时频分布中提取得到的冲击能量进行深入分析。

基于以上分析，本文从能量的角度刻画弓网冲击所引起接触网垂向振动加速度的高频特性，基于CEEMDAN-SPWVD时频分析计算移动滤波边际谱，并进行归一化处理，提出采用接触网边际指数(Catenary Marginal Index，CMI)诊断接触网硬点。

1 CEEMDAN-SPWVD时频分析方法

1.1 CEEMDAN原理

经验模态分解(Empirical Mode Decomposition，EMD)[15]是一种处理非平稳信号的方法，其原理是将非平稳信号按不同波动尺度分解为多个固有模态函数(Intrinsic Mode Function, IMF)分量。而集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[16]在EMD算法中做了一定改进，该算法向原始信号中添加多组不同的正态分布白噪声，然后对多组信号分别进行EMD，并将分解得出的固有模态函数分量进行求和平均，可以有效抑制EMD中模态混叠的现象。EEMD虽然改善了EMD的模态混叠问题，但是由于加入白噪声，也带来了其他问题：

(1)白噪声在集总平均之后基本抵消，但存在残留，重建之后噪声不可忽略；

(2)集总平均次数一般在几百次以上，非常耗时；

(3)信号加上不同的白噪声可能会产生不同数量的模函数。

自适应噪声的完整集合经验模态分解(Complete EEMD with Adaptive Noise，CEEMDAN)[23]算法是在EEMD算法基础上进行优化。对信号添加多组经过模态分解的自适应白噪声，减少了IMF中的噪声，有效克服了EEMD受噪声影响，重构误差较大的缺点。并且集总平均次数由几百量级降至几十量级。既可以减少重构误差，也可以减少计算时间。另外CEEMDAN还解决了EEMD中信号加入不同噪声时分解出不同IMF阶数的问题。

CEEMDAN详细计算步骤流程见图1。

图1 CEEMDAN计算步骤流程

Step1令s(n)表示原始受电弓垂向加速度信号;wi(n)为第i次添加的服从标准正态分布的白噪声信号;εk为第k个信噪比;Ek(·)为通过EMD算法产生第k个IMF的算子;M(·)为通过EMD算法产生局部均值函数，即上下极值点包络线的平均值;si(n)为第i次添加了经过EMD分解后噪声的原始信号，si(n)=s(n)+ε0E1[wi(n)]，i为试验次数，i=1,2,…,I。

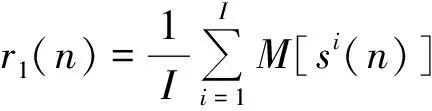
Step3为了得到第2个模态分量，继续对r1(n)+ε1E2[wi(n)]进行EMD分解，得到其多组局部均值函数，平均后得到CEEMDAN的第2个残余量，即

( 1 )

IMF第2个模态分量可以表示为

IMF2(n)=r1(n)-r2(n)

( 2 )

Step4第k+1个残余量信号计算方法与Step3相同，k=2,…,K。

( 3 )

IMF第k+1个模态分量可以表示为

IMFk+1(n)=rk(n)-rk+1(n)

( 4 )

Step5执行Step4直到所有残余量序列的极值点个数小于等于两个，表示残余量序列不可继续进行分解。

最终得到的残差为

( 5 )

因此原始受电弓垂向加速度信号被分解为

( 6 )

通过以上算法流程可以看出，CEEMDAN在每个分解阶段，都能够通过系数εk选择信噪比。试验证明该方法相比于EEMD，不仅计算量更少，而且对原始信号的重构精度更高。

信号通过CEEMDAN分解为不同的IMF，再分别进行后续的时频分析，能够有效减少频域方向上交叉项的干扰。

1.2 SPWVD原理

1948年，法国学者Ville与美国物理学家Winger提出维格纳-威利分布(Wigner-Ville Distribution，WVD)时频分析方法[29-30]。

连续时间信号x(t)的Wigner-Ville分布定义为

(7)

式中：x(t)为实信号；t为时间；τ为延时；f为频率；*为共轭转置。

WVD在单分量信号的时频特征提取中取得了良好的效果，具有最好的时频聚集性，然而由于是典型的二次型变换，在多分量信号的时频分析中会存在交叉干扰项。虽然进行CEEMDAN分解后再进行WVD变换能减少频域方向上的交叉项干扰，但并不能减少时域方向上的干扰。

因此，本文采用加窗的方式对信号的WVD时频分布进行时域、频域上的平滑处理。

连续时间信号x(t)的平滑伪魏格纳-维利分布(Smoothed Pseudo Wigner-Ville Distribution，SPWVD)定义为

SPWVg,h(t,f)=∬g(u)h(τ)x(t-u+τ/2)·

x*(t-u-τ/2)e2jπfτdudτ

( 8 )

式中：g(u)、h(τ)分别为频域和时域方向上的窗函数。

2 接触网硬点诊断的边际指数法

由于受电弓垂向加速度具有很强随机性，因此采用接触网边际指数法将加速度数据从高频转换成高稳定性的边际指数，更利于诊断接触网硬点的位置。

接触网边际指数法计算流程见图2。

图2 接触网边际指数法计算流程

Step1结合CEEMDAN、SPWVD计算受电弓垂向振动加速度的时频分布为

( 9 )

式中：D(t,f)为计算得到的时频分布；SPWVD(·)为经过单次SPWVD变换后得到的时频分布。

Step2通过若干硬点时频图确定弓网动态响应数据能量主要分布范围[FL,FH]。

Step3计算时频分布的移动边际谱为

(10)

式中：K为向前加窗的时间窗长；[FL,FH]为Step2中确定的带通滤波范围。

Step4将接触网划分成单元，单元长度一般取为50 m。

Step5计算各单元移动边际谱的最大值Mmax，记为单元边际值。

Step7计算接触网边际指数CIMi为

(11)

Step8超限判断，并记录对应的位置信息(根据对大量测试数据的计算分析，对超限判断阈值取16.0)。

3 实例分析

利用本文方法对实测的受电弓垂向振动加速度进行分析，诊断接触网硬点，通过用同一线路区段的检测数据多次试验，进一步验证本文评判方法的稳定性。

3.1 时频特性分析

如图 3所示，在该区段出现了较为明显的两次独立的冲击，对这段信号进行CEEMDAN分解。

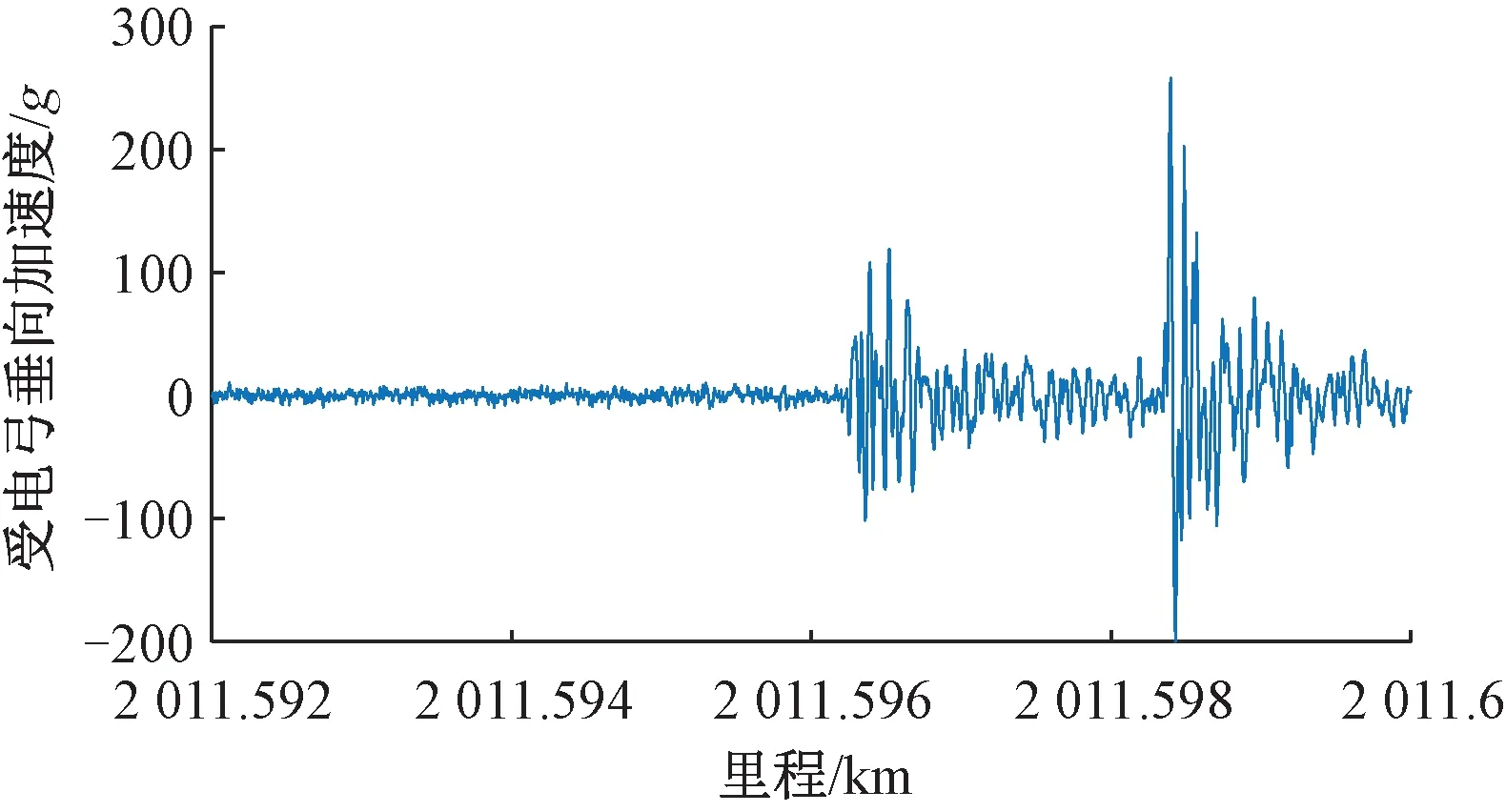
图3 受电弓垂向振动加速度原始信号

图4 各阶IMF信号及残余项信号波形图

如图 4所示，该区段原始信号被分解为8个IMF信号和一个残余信号。

随后将分解得到的IMF及残余项进行SPWVD变换，见图5。

图 6为图 5中各阶IMF及残余信号SPWVD时频叠加所得的CEEMDAN-SPWVD时频分布，而图 7为原始信号直接进行WVD变换所得，在图 7中能观察到在原始信号两个单点冲击位置之间出现明显的干扰项，与之相比，CEEMDAN-SPWVD变换所得到的时频图不管是在时域方向还是频域方向，均较好地抑制了交叉项的干扰，同时还具有良好的时频聚集性。

图5 各阶IMF信号及残余项信号SPWVD时频图

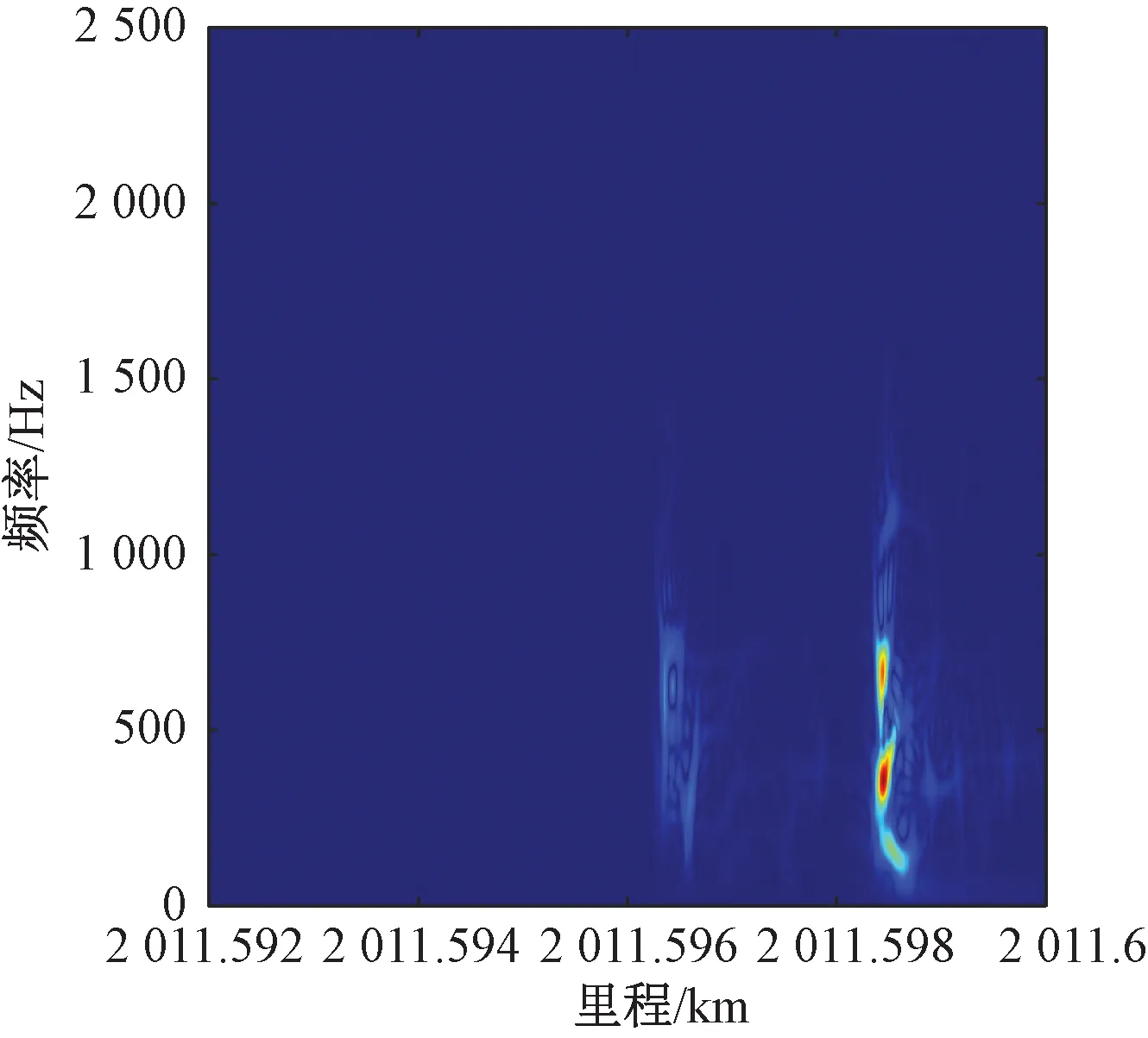
图6 信号CEEMDAN-SPWVD时频图

图7 信号WVD时频图

3.2 硬点诊断

通过对若干硬点，包括接触线硬弯、各种零部件或其线夹状态异常、绝缘器状态异常、锚段关节过渡不平滑以及刚性接触网状态异常的加速度数据进行时频分析，确定弓网动态响应数据能量主要分布在20～800 Hz，因此在进行移动边际谱计算时对时频图做带通滤波处理。即在计算移动边际谱时只选取20～800 Hz范围内的时频分布。

由时频分布加移动窗计算得到边际谱的过程见图8，在该算例中，取时域方向窗长点数K=600。能清晰观察到时频图中存在能量的位置在移动滤波边际谱图中均以峰值的形式得以体现。

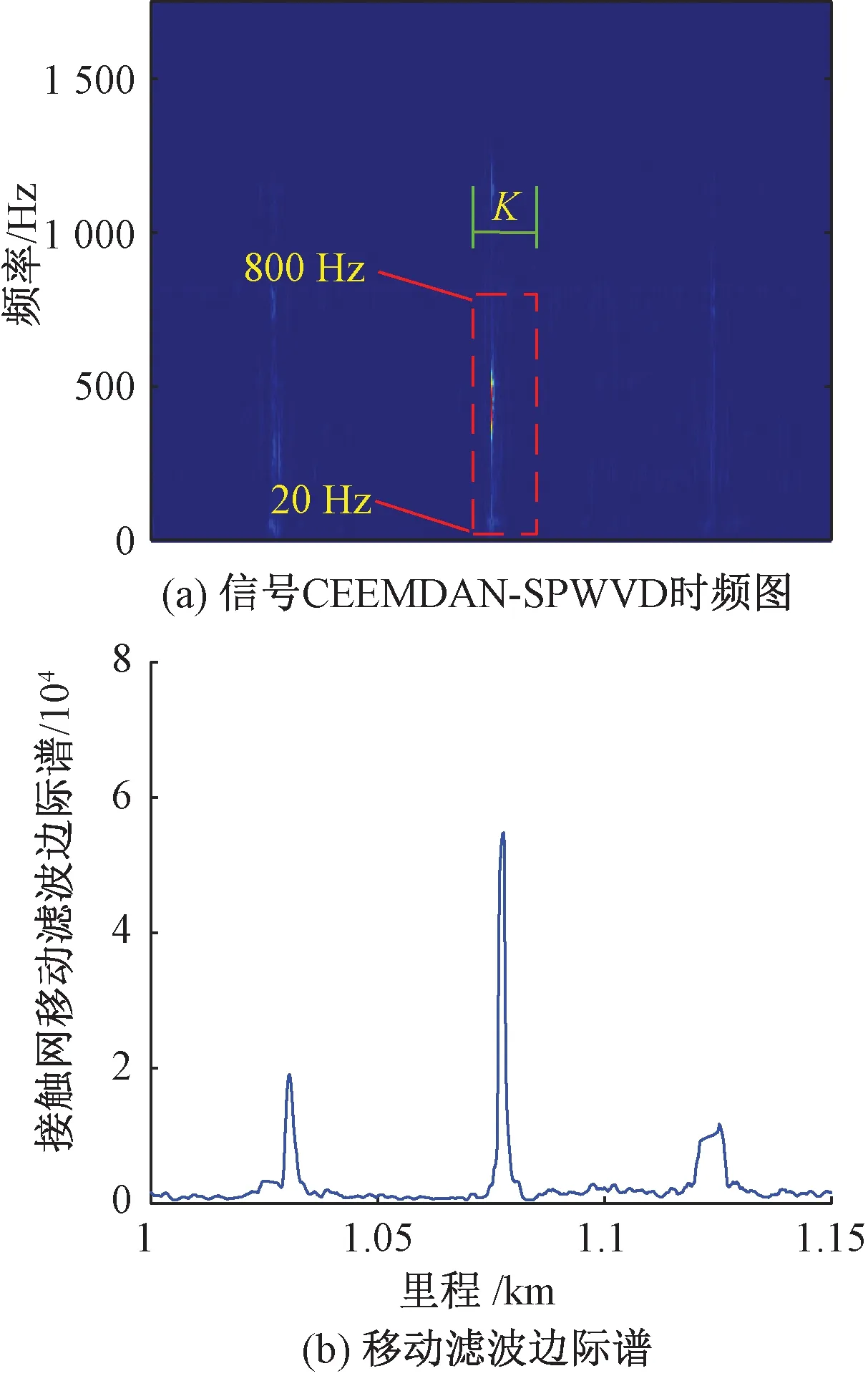
图8 信号移动滤波边际谱计算图

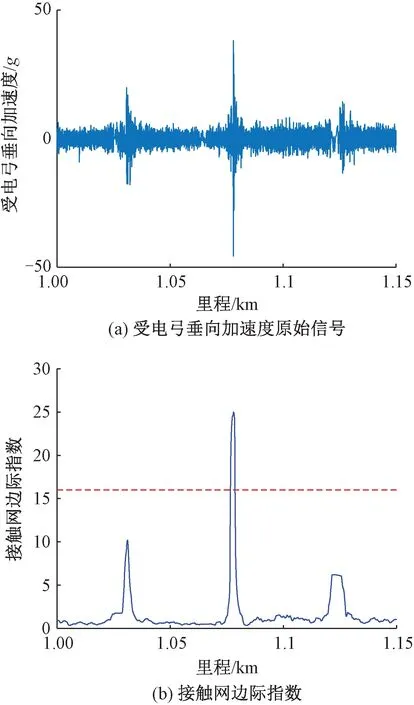
图9 加速度原始信号及对应接触网边际指数

可以看出，当接触线存在硬点时，弓网之间会发生较大的冲击，受电弓垂向振动加速度呈先增后衰减的过程，虽然不一定会出现特别大的幅值，但积累的冲击能量大。

为了验证CMI方法的有效性，对铁路线路进行了现场复核。在该中心柱的T形定位器的定位线夹处发现轻微的接触线硬弯，据现场检测人员介绍，初步判定为接触网放线时施工不规范所导致。同时现场中心柱两侧的两个转换柱分别与图 9(b)中接触网边际指数图中中心柱两侧间隔50 m左右的较小峰值相对应。

通过以上分析可以发现，接触线硬弯的现象会导致车辆经过此处时受电弓振动较大，可能会造成导线的异常磨耗。同时，以上分析结果证明了接触网边际指数能有效地诊断接触网硬点。

3.3 稳定性分析

利用接触网边际指数分析两次通过同一路段的受电弓垂向加速度数据。受电弓垂向加速度的原始信号和接触网边际指数见图10。对比图 10(a)和图10(b)可以看出受电弓垂向振动加速度信号的幅值随机性较大，难以确定评判阈值，而在图 10(c)和图 10(d)中以能量角度刻画的受电弓振动特性的接触网边际指数图中，可以观察到在K1+078处均出现一个独立的较大峰值。

图10 两次通过K1+078附近的受电弓垂向振动加速度波形及对应的接触网边际指数

为验证CMI在不同速度级下的重复性，计算2次以速度130 km/h和2次以速度150 km/h运行检测得到的共4次数据的CMI，见图11。由图11可以看出，由受电弓垂向加速度计算出的接触网边际指数每次都在该处出现峰值，而且波形相似，并且归一化处理后以不同速度多次通过同一路段检测数据计算得到的评判指标也趋于一致。由此表明本文提出的评判方法是稳定的，而且具有很好的重复性。再利用其分布规律可以较容易地确定评判阈值。