基于子结构的轨道系统基础结构参数识别方法

2022-06-01陈华鹏刘昌雨

铁道学报 2022年5期

叶玲，陈华鹏，刘昌雨

(华东交通大学土木建筑学院，江西南昌 330013)

随着高铁运输的迅猛发展，轨道运输在整个交通运输系统中占有越来越重要的位置。开展车辆荷载作用下超长线状结构参数识别方法研究，识别结构的损伤状况，实现车辆参数和结构参数的实时监控和智能化管理，对保障城市交通正常运作至关重要。近年来，越来越多的学者开始关注由于车辆荷载引起的地铁轨道和桥梁这一类超长线状结构的损伤识别。Zhou等[1]提出了一种隧道结构损伤识别方法，确定了隧道结构杨氏模量与耦合共振频率的关系。Zhou等[2]提出了一种基于波传播的结构健康评估方法，以确定隧道结构的整体刚度，进一步评价隧道结构的服役性能。Liu等[3]提出了一种基于移动荷载作用下大跨度轨道桥梁位移响应灵敏度分析的损伤识别方法。Chen等[4]提出了一种基于有限测点响应同时识别结构损伤和力的方法。Ling等[5]提出了一种未知移动力作用下结构损伤识别方法，该方法以结构单元刚度变化为损伤指标，以动力响应灵敏度为优化方向。文献[6-8]通过对随机荷载作用下系统动力响应灵敏度特点的研究，提出了一种用于识别大型结构的损伤识别方法，并将其应用到大跨度轨道桥梁结构中，识别了车辆荷载作用下的桥梁结构损伤。Majumder等[9]将车辆系统简化为单自由度移动质量块，研究了基于车辆动力响应和桥梁结构动力响应对桥梁结构进行损伤识别的方法。

上述方法在对地铁轨道和桥梁这一类超长线状结构进行有限元建模时，通常只能选取一定长度的结构作为研究对象，这种选取一定长度模拟无限长轨道的方法，缺少物理意义，且在识别结构损伤时，也容易因为边界问题引起识别误差，同时，由于这类结构本身结构规模大、待识别参数多，极大地限制了识别效率。子结构参数识别法将子结构法和参数识别方法相结合，将大型结构划分为若干个子结构，在保证相同条件下，有效减少研究对象的单元数目，提高算法的精度和效率，为超长线状结构的参数识别提供了新思路。Weng等[10]在力和位移兼容性的约束下，分解整体结构的模态数据，提出了一种新的逆向结构损伤识别方法，可以高精高效的识别结构损伤。随后Koh等[11]采用“分而治之”的战略思想解决了当子结构和整体结构差别较大时，很难在数值上获得合理准确结果的难题，给出了渐进结构识别方法。Yun等[12]采用子结构识别法和子矩阵缩放因子，克服了未知参数相关性等问题。Koh等[13]提出了一种不需要界面测量信息的子结构损伤识别方法。Law等[14]提出了一种从支撑激励下结构的加速度响应中识别结构间耦合力的方法，并基于动态响应灵敏度分析对所识别的耦合力进行了局部结构损伤检测，该方法在状态空间域中建立了耦合力的识别方法，并用阻尼最小二乘法求解。

为了高精高效的识别轨道系统基础结构参数，本文提出了一种基于子结构的超长线状结构参数识别方法。在车辆荷载作用下，将子结构界面力作为待识别子结构的未知外荷载，表达为切比雪夫多项式，推导系统动力响应关于结构参数和界面力参数的灵敏度矩阵，根据车轨系统参数同步识别方法[15]，同时识别轨道子结构参数和界面力参数。通过一个车辆-轨道交互系统数值算例验证了基于子结构的轨道系统基础结构参数识别方法的精度和效率。

1 独立子结构的动力响应分析

1.1 车辆-轨道交互系统的运动方程

车辆系统离散为附有二系弹簧的多刚体整车模型。假设车辆的各个组成部件都关于各自质心前后、左右对称，取沿纵向线路对称的半车结构进行研究。定义位移和力的方向以竖直向下为正，转角和力矩的方向以逆时针方向为正，将每个车辆看作一个单元，则半车模型共有10个自由度，见图1，车辆系统位移响应矩阵Xa可记为

(1)

式中：xc和φc分别为车体竖向位移和转角；xeu和φeu(u=1,2)分别为车辆第u个转向架竖向位移和转角；xwi(i=1～4)为车辆第i个车轮竖向位移。

图1 车辆模型

由Hamilton原理[16]，可得车辆系统运动方程

(2)

列车的质量、阻尼和刚度矩阵分别可表示为

(3)

(4)

(5)

式(3)～式(5)中：Mc和Me分别为列车车体质量和转向架质量；Jc和Je分别为列车车体点头惯量和转向架点头惯量；Cs1和Cs2分别为一系悬挂装置和二系悬挂装置的阻尼；Ks1和Ks2分别为一系悬挂装置和二系悬挂装置的刚度；L1为单个转向架上两车轮中心之间的半距；L2为车体上两个转向架中心之间的半距。

本论文仅考虑车辆荷载对超长线状结构的竖向作用，将隧道-土体简化为弹性块式支承，用弹性支承块式无砟轨道模型模拟轨道结构，弹性支承块式无砟轨道模型由钢轨、混凝土道床板、隔离层及混凝土底座等组成，见图2。由于轨道结构沿纵向线路横向对称，故取对半轨道结构研究。钢轨用Bernoulli-Euler梁结构模拟；轨枕简化为仅在竖向发生振动的质量块Ms，且沿轨道长度方向等间距布设；钢轨与轨枕之间，轨枕与道床之间均通过弹簧-阻尼器连接，两组弹簧-阻尼器刚度系数和阻尼系数分别记为kp,cp和kb,cb。

图2 弹性支承块式无砟轨道模型

因轨道模型具有周期性结构特性，故可根据轨枕所在位置划分钢轨结构，形成轨道单元，则轨道系统转化为由多个轨道单元首尾相连而成的结构。其中轨道单元见图3。弹性支承块式无砟轨道的振动主要体现在钢轨和混凝土支承块上。钢轨只考虑竖向位移和转动，轨枕只考虑竖向位移，定义位移和力的方向以竖直向下为正，则一个轨道单元包含5个自由度。

图3 轨道单元模型

轨道单元的质量矩阵可看作钢轨质量矩阵与轨枕质量矩阵的叠加，具体表达式为

Mcell=Mr+Ms

(6)

式中：

(7)

(8)

其中，mr为单位长度(1 m)钢轨质量；ms为轨枕的质量；l为一个轨道单元中钢轨的长度。

同理，轨道单元的刚度矩阵表达式为

Kcell=Kr+Ks

(9)

式中：

(10)

(11)

其中，I为钢轨转动惯量；E为钢轨弹性模量；kp和kb分别为钢轨垫片和道床的刚度。

轨道单元的阻尼矩阵表达式为

Ccell=Cr+Cs

(12)

式中：

(13)

式中：cp和cb分别为钢轨垫片和道床的阻尼。

钢轨阻尼矩阵采用瑞利阻尼矩阵，可以表示为钢轨质量矩阵和刚度矩阵的线性组合，即Cr=αMr+βKr，α和β分别为瑞利阻尼系数，根据结构动力学原理，α、β分别为

(14)

其中，η1和η2分别为钢轨的一阶和二阶频率；ξ1和ξ2分别为钢轨相关的一阶和二阶阻尼比。

轨道系统总的质量矩阵、阻尼矩阵和刚度矩阵可以通过组集轨道单元的质量矩阵、阻尼矩阵和刚度矩阵得到，轨道系统的运动方程最终可表示为

(15)

Nbj,i=

(16)

式中：xh,i(t)为t时刻第i个车轮经过钢轨的距离；j为t时刻第i个车轮已通过的钢轨单元个数。

t时刻车轮通过的距离xh,i(t)可以表示为

(17)

式中：x0为起始时刻第4个车轮所在位置到钢轨最左端的距离；V为车辆行驶速度，本文车速定义为恒速。

本文采用余弦函数表示钢轨焊接接头和钢轨波磨的形状，即轨道位移不平顺表达为

(18)

式中：μ和分别为轨道位移不平顺的统计波深和波长，根据轨道线路实地测量获得；L为实际的轨道位移不平顺长度。

车辆与轨道之间采用非线性Hertz接触弹簧模拟轮轨法向接触力，则轮轨法向接触力[17]可以表达为

(19)

式中：G为轮轨接触常数,m/N2/3；δX为轮轨间的弹性压缩量，其值根据车轮接触面形状有不同取值，m。

对于磨耗型踏面车轮计算式为

G=3.86R-0.115×10-8

(20)

对于锥形踏面车轮计算式为

G=4.57R-0.149×10-8

(21)

式中：R为车轮半径,m。

轮轨间的相对位移由该时刻，车轮的竖向位移和车轮所在钢轨接触点处钢轨的竖向位移确定，即

δX=xw,i-xr,ii=1～4

(22)

式中：xw,i为第i个车轮的竖向位移,m；xr,i为第i个车轮所在钢轨处钢轨的竖向位移,m。

当轮轨接触界面存在轨道不平顺Xirr时，轮轨法向接触力可以表达为

(23)

式中：x=xw,i-xr,i-xirr,i；xirr,i为第i个车轮所在钢轨处的轨道位移不平顺，m；xirr,i=Xirr(xh,i(t))。

令Kw=G-3/2，则轮轨法向接触力可以表达为

(24)

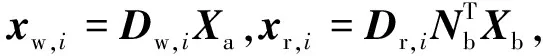
(25)

将式(2)、式(15)、式(25)组合到一起，即可得模拟车辆荷载作用下超长线状结构的车辆-轨道交互系统运动方程，表示为

(26)

由式(3)～式(5)，可获得车辆系统质量矩阵Ma、刚度矩阵Ka和阻尼矩阵Ca，通过式(6)、式(9)、式(12)，可组集得到轨道系统质量矩阵Mb、刚度矩阵Kb和阻尼矩阵Cb。在给定的时间序列中，可写出所有指示矩阵D和形函数矩阵N。该运动方程可通过基于Newmark的时间步内交叉迭代算法[15]计算得到。

1.2 子结构方法的应用

应用子结构方法[18]划分轨道结构，根据是否有车辆经过，可以将轨道结构划分有车辆荷载作用的轨道子结构和没有车辆荷载作用的轨道子结构。轨道整体结构划分为轨道子结构的示意图见图4，根据是否有车辆通过，可化分为有车辆荷载作用的轨道子结构1和没有车辆荷载作用的轨道子结构2。Fi1和Fi2分别为轨道子结构1和轨道子结构2的界面力，车辆以速度V在轨道子结构1上运动。

图4 轨道整体结构划分子结构示意

对于轨道子结构1，同时受到车辆荷载和子结构界面力作用，轨道子结构1的运动方程可以表达为

(27)

由式(27)第一个方程式可得

(28)

界面力Fi(1)用切比雪夫正交多项式表示，即

(29)

式中：m为正交多项式的项数；c为界面力正交系数；T为切比雪夫正交基，计算式为

(30)

式中：Dt为车辆荷载的持续时间。

轨道子结构1上同时受到车辆荷载和界面力作用Q(1)，计算式为

Q(1)=Ds(1)Ns(1)fwr(1)-Fi(1)

(31)

将式(31)代入式(28)中，轨道子结构1运动方程可表示为

(32)

结合式(26)、式(32)，即可得到轨道子结构1和车辆系统组成的车辆-轨道交互系统运动方程为

(33)

同理，对于轨道子结构2，其运动方程可以表示为

(34)

式中：上标(2)表示第二个轨道子结构。

由式(34)第一个方程式可得

(35)

式(35)右边为相邻轨道子结构对轨道子结构2的界面力，该界面力同样可以用切比雪夫正交多项式表示，同式(29)，作用在轨道子结构1和轨道子结构2上的界面力为一对大小相等，方向相反的作用力和反作用力，轨道子结构2的运动方程可以表达为

(36)

同理，式(33)和式(36)均可以通过时间步内交叉迭代算法[15]计算。

2 基于子结构的轨道系统基础结构参数识别方法

轨道结构损伤体现在结构刚度的弱化，故将结构参数定义为轨道系统中钢轨的单元刚度的变化，对结构参数的识别即为对钢轨单元刚度的识别。定义为

(37)

(38)

由于轨道刚度矩阵Kb是由轨道结构中钢轨的单元刚度EI组成的，将式(38)带入轨道刚度矩阵表达式中，即可得到轨道刚度矩阵关于钢轨单元刚度相对变化量的一阶导∂Kb/∂λp。

子结构界面力用切比雪夫正交多项式表示，则对界面力的识别即为对正交多项式系数cm的识别，需要识别的正交多项式系数的数量为m。计算式(33)关于结构参数的一阶导数，可获得轨道子结构1下系统动力响应关于结构参数λp的灵敏度矩阵

计算式(33)关于正交系数cm的一阶导数，可获得轨道子结构1下系统动力响应关于界面力正交系数cm的灵敏度矩阵

(40)

计算式(36)关于结构参数的一阶导数，可获得轨道子结构2下系统动力响应关于结构参数λp的灵敏度矩阵

(41)

计算式(36)关于正交系数cm的一阶导数，可获得轨道子结构2下系统动力响应关于界面力正交系数cm的灵敏度矩阵

(42)

式(39)～式(42)可以通过交叉迭代算法计算。

本章采用基于灵敏度分析的有限元模型修正方法，将通过子结构模型计算得到的系统加速度响应与整体结构同条件下测量得到的系统加速度响应的残差作为目标函数J，可以表示为

(43)

参数识别过程中需要修正的参数γ(1)由结构参数λ以及界面力正交系数c组成，其中，λ=[λ1λ2…λp]T，c=[c1c2…cm]T，γ(1)=[λ1λ2…λpcp+1cp+2…cp+m]T。基于子结构法的参数识别方程可以表示为

(44)

基于子结构的轨道系统基础结构参数识别方法的具体流程见图5。

图5 基于子结构的轨道系统基础结构参数识别流程图

基于子结构的轨道系统基础结构参数识别方法具体步骤如下：

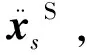
Step2当迭代次数k=1时，利用式(39)、式(41)计算系统加速度响应关于待识别结构参数λ的灵敏度矩阵Sλ；利用式(40)、式(42)计算系统加速度响应关于界面力参数c的灵敏度矩阵Sc。

Step3根据参数同步识别方法，利用式(44)计算出当前迭代步的待识别结构参数λk和ck。

Step4判断待识别参数λk和ck是否满足优化过程的目标函数收敛准则，即|J|≤Tolerance，满足条件，则迭代停止；若不满足，令k=k+1，重复Step1—Step4，直到目标函数满足收敛条件后，迭代停止，得到参数最终的识别结果λk和ck。

3 车辆-轨道交互系统参数识别数值算例

本文用于模拟轨道交通系统的车辆模型和轨道模型分别见图1和图2。车辆在轨道上运行距离为98.1 m，轨道单元长度l=0.545 m，经过180个轨道单元，车辆从轨道左侧匀速通过轨道，车速为恒速V=200 km/h，考虑波长和波深分别为3.3 cm、25 μm的轨道不平顺，时间步长取为1×10-4s，时程曲线见图6。轨道各参数见表1，车辆各参数见表2。以车辆荷载下的轨道结构为研究对象，将轨道结构在节点91处划分成两个轨道子结构，轨道子结构有限元模型见图4。选取时间历程前0.5 s的测量动力响应作为子结构结构参数识别的测量响应，前0.5 s内车辆仅在轨道子结构1上运行。采用基于子结构的参数识别方法计算结构参数和界面力参数。

图6 轨道不平顺时程曲线

表1 轨道参数

表2 车辆参数

车辆荷载作用下轨道子结构单元刚度发生变化的各种工况见表3，工况1为轨道结构单元81发生20%的单元刚度折减，此时发生单元刚度变化的单元处于轨道子结构1上，故可仅以轨道子结构1为研究对象，同步识别轨道子结构1未知界面力作用下的车轨交互系统参数和界面力参数；工况2为在工况1的基础上，对测量响应加入5%噪声的情况；工况3为轨道单元81和单元122都出现单元刚度折减，变化程度分别为20%和30%的情况，单元81位于轨道子结构1，单元122位于轨道子结构2中，同时选取两个轨道子结构作为研究对象，同步识别结构参数和界面力参数；工况4为在工况3的基础上，测量响应加入5%噪声的情况。

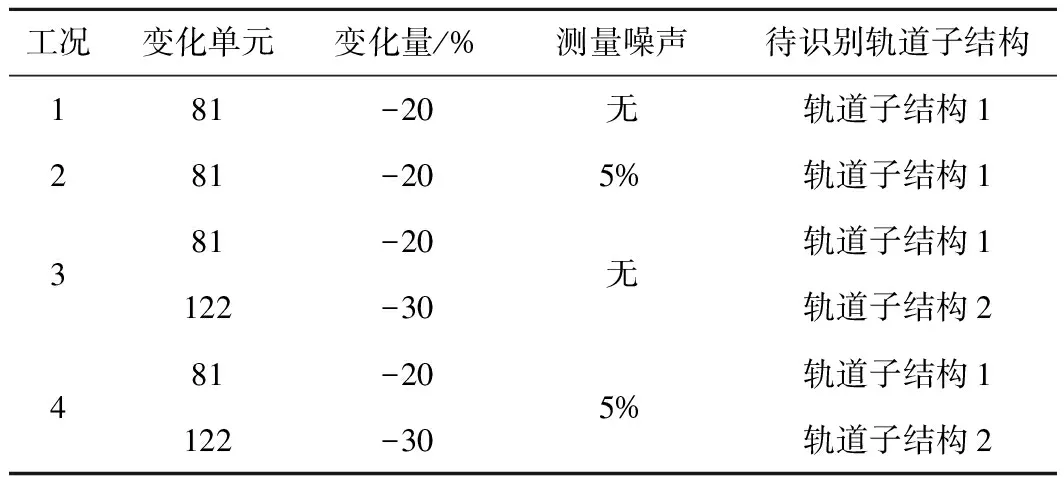
表3 车辆荷载下子结构参数识别的各种工况

本文测量噪声用一组正态随机分布数据进行模拟，加了噪声之后的测量加速度响应可表示为

(45)

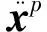
选取工况1和2为研究对象，即以轨道子结构1为目标子结构，界面力Fi1和Fi2作为轨道子结构1的等效输入力，识别轨道子结构1的结构参数和界面力参数，其中，界面力表达为切比雪夫多项式，阶数取为30。子结构参数识别方法的目标函数为通过子结构模型计算得到的系统加速度响应与整体结构同条件下测量得到的系统加速度响应的残差，故整体结构条件下测量得到的系统加速度响应为已知条件，理论界面力可通过将整体轨道动力响应带入式(32)计算得到。无测量噪声(工况1)和5%测量噪声(工况2)下轨道子结构1的界面力时程曲线分别见图7、图8。工况1和工况2中所识别界面力与理论界面力的相对误差e计算式为

(46)

工况1和工况2中所识别界面力的相对误差见表4。表4可知，在无测量噪声条件下，界面力Fi1和Fi2识别结果与相应理论界面力的相对误差值为3.36%和3.26%，两者的时程曲线非常吻合；在5%测量噪声条件下，界面力Fi1和Fi2识别结果与相应理论界面力的相对误差值为10.68%和10.77%，相对误差值变大，虽然出现了微小的偏差，但是两则的时程曲线基本一致。

图7 工况1理论界面力与识别界面力时程曲线

图8 工况2理论界面力与识别界面力时程曲线

表4 工况1和工况2中所识别界面力的相对误差值 %

图9 结构参数识别结果

不考虑噪声和考虑5%噪声条件下，以轨道子结构1为研究对象时，识别的结构参数识别见图9。由图9(a)、图9(b)可知，不考虑噪声条件时，轨道结构单元刚度发生变化的位置和程度可以准确识别出来；考虑5%测量噪声时，出现了识别误差，但是误差较小，即仍然可以准确的识别出轨道结构单元刚度发生变化的位置和程度。以工况3和工况4为研究对象，即轨道子结构1和轨道子结构2上均存在单元刚度发生变化时，需要将轨道子结构1和轨道子结构2同时为识别对象，将轨道子结构1识别出的界面力作为轨道子结构2的输入荷载，分析工况3和工况4，识别在车辆荷载作用下的系统参数和界面力参数。无测量噪声(工况3)和5%测量噪声(工况4)下轨道结构单元刚度相对变化量的识别结果见图9(c)～9(f)，轨道子结构1和轨道子结构2中发生单元刚度变化的轨道单元位置和程度均能准确识别出来，考虑测量噪声条件时，轨道子结构的边界单元以及发生单元刚度变化的单元附近的单元出现了识别误差。

为了验证基于子结构的轨道系统基础结构参数识别方法的高效性，与通过整体参数识别法计算同一车轨交互系统模型参数的结果对比。整体参数识别法和子结构参数识别法计算车轨交互系统模型参数所用的时间见表5。由表5可知，子结构参数识别法迭代一步仅需44.59 s，需迭代8次，所用总时间为356.7 s；整体参数识别法迭代一步需129.78 s，需迭代13次，所用总时间为1.687×103s，约为子结构参数识别法计算所用时间的4.73倍，这是由于轨道整体结构的自由度个数为905个，轨道子结构1的自由度个数只有455个，在识别过程中每一次迭代的动力响应和动力响应灵敏度矩阵的维数由整体参数识别法的905×(5×103)减少至子结构参数识别法455×(5×103)，同时所需识别的参数数量也由整体参数识别法的180个减少至子结构参数识别法的120个。与整体参数识别法对比，子结构参数识别法在计算过程中包含更少的自由度个数和待识别参数个数，大幅减少了计算时间，有效提高了计算效率。