微电阻梁的多物理场仿真研究分析

杨朵玉

（华中师范大学物理科学与技术学院 湖北 武汉 430070）

0 引言

电子元器件元件在日常生活中的各种产品中广泛存在着。微型电阻器通电后可以立即产生快速且准确的驱动或结构运动，可用于许多应用领域，在这些应用中，需要瞬时地对器件施加小扰动或小挠曲。目前已有将微电阻梁用来研究制作光开关和传感器等的研究先例。这些电子元件在电路通电时会产生焦耳热，在焦耳热的作用下，物体会发生热膨胀而使物体结果发生变形。当温度到达物质的熔点时，还会发生熔断等现象[1]。近年来，微电阻梁传感器以诸多优点在世界范围内引起了广泛的关注。微电阻梁传感器有着灵敏度高、体积小、易于排列以及易于获得等优点[2]。微悬臂梁传感器可以实现高灵敏度、特异性和阵列式的生化检测与测量，因此在生物化学物质的检测中受到了广泛的研究关注[3]。当分子附着在微型电阻梁的表面上之后,有一个变化的压力作用在微型电阻梁表面,导致上下表面存在着压力差,使电阻梁发生轻微弯曲,通过读出系统检测微型电阻梁的弯曲量实现生物化学分子检测。微型电阻梁传感器由于具有这些优点，已经应用于基因组学、蛋白质组学和疾病诊断等领域[4]。

本文采用多物理场仿真软件COMSOL Multiphysic 软件建立了微阻梁的多物理场模型，设定了铜微梁的密度、热导率(轴向、纵向)及恒压热容，探讨了铜微梁通电后产生的热影响所带来的后果，以及电流参量对热变形的影响规律，为研究微电阻梁的热损伤机理提供了一定的理论指导，为应用微电阻梁制作光开关和传感器等器件提供参考[5]。

1 理论建模

COMSOL Multiphysics 软件通过求解偏微分方程(单场)或偏微分方程组(多场耦合)来实现真实物理现象的仿真，用数值计算方法求解真实世界的物理现象。在COMSOL 中可对模型的材料属性、网格划分以及边界条件等进行参数化定义。COMSOL 中预定义的多种物理场应用模式不仅能够解决许多常见的物理问题，使用者也可以输入自定义的偏微分方程（PDEs），并指定其与软件内嵌方程和物理场之间的关系。本模型可阐明在一个模型中耦合热、电及结构分析的能力，该模型中通过流通电流来使梁受热改变，电流通过电阻时产生热量，当温度上升到一定高度时通过热膨胀使梁产生位移，是一个很好的多物理场建模示例[6]。微电阻梁的材质是铜，拱形微电阻梁的截面为梯形，如图1 所示。微电阻梁的高度和宽度均为1μm，长度是13μm。将微电阻梁的两个底脚牢固的固定在基板上，两底脚之间施加电势差使电流流过微电阻梁。电流流过电阻时会使电阻的电阻率发生变化，由于所用材质为金属材料，金属材料的电阻率随温度的升高而增大，在有电流通过微电阻梁时，使金属材料产生热量。微电阻梁在开放环境中工作，因此产生的热量会消散到空气中。而当物体温度发生改变时，物体由于外在约束以及内部各部分之间的相互约束，使其不能完全自由胀缩而产生一种力的作用，我们把它叫做热应力[7]。由热导致的应力将对材料施加载荷，并且能使梁变形。

图2 显示了微阻梁的三维模型，铜微梁的长度为13 μm，高度和宽度均为1 μm。两端的底部将其牢固地固定在基板上。底部之间施加的0.2 V 的电势使其产生电流，产生的电流通过梁而产生焦耳热。通过使用焦耳热和热膨胀预定义多物理场接口，可以自动添加三个物理场的方程，包括必要的多物理场耦合。在本例中，物理场方程描述了电流、热传导以及结构力学问题。由于材料的电阻率，电流使结构受热。梁在开放环境中操作，因此生成的热量会消散到空气中。热致应力将对材料施加载荷，并使梁变形。可以假设电导率恒定，将其作为第一个近似。但是，导体的电阻率随着温度的升高而增大，微电阻梁的温度也随之升高。在使用铜的情况下，金属电阻的电阻率与温度之间的关系在很大的温度范围内近似为线性变化[8]：

其中，α 表示温度系数。根据定义电阻率的关系，可获得导体的温度依存性；电导率即为其方程1 倒数（σ= 1/ρ）。

对于传热方程，将面向基板的底部边界设为323 K 的恒温。使用传热系数h 为5 W/（m2·K）、外部温度Tinf为298 K 的热通量边界条件对其他边界中的对流空气冷却进行模拟。标准约束可以处理底部与基板的刚性连接。对于本预测实验模型中具体用到的铜片电阻热物性参数见表1。

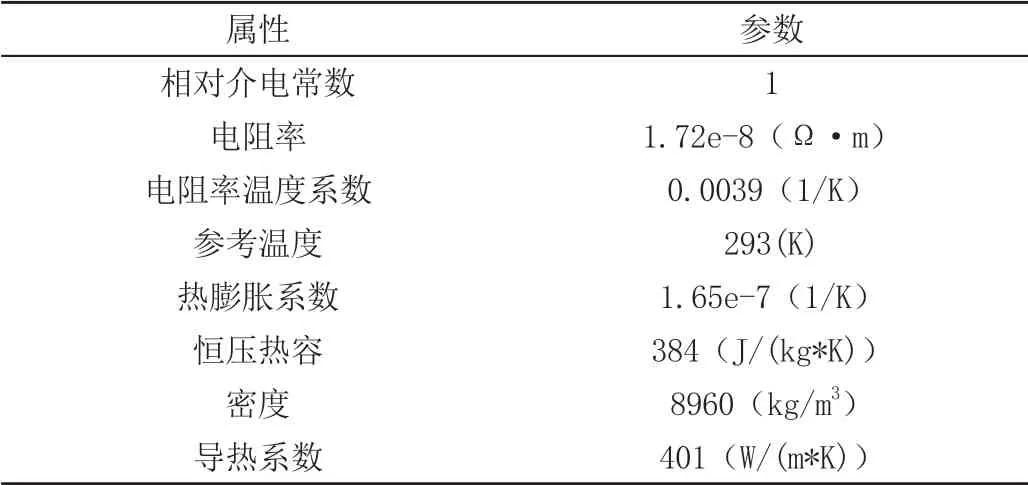
表1 模型材料参数表

本文中使用COMSOL 中的用户控制网格功能对铜微梁进行网格剖分，可以大大加快求解速度，减少剖分网格带来的计算成本，使其收敛到最优解，铜微梁网格剖分图如图2所示。

2 模型解析

该模型涉及满足电流产生的一切条件，即电流守恒条件且满足电流守恒定律，因此需要利用电流守恒方程。电流产生的焦耳热需要对流到空气中，所以需要一个热传导方程。温度改变带来电阻的变化，因此首先采用传热与电流的二维耦合。同时，温度的升高会引起材料的热膨胀，因此在固体力学中应考虑热变形问题。因此，三个电场的耦合、固体传热和固体磁性的耦合是必要的。在Comsol 中，两个物理磁性模块，即电场中的焦耳热和结构能量学中的固体磁性的耦合是必要的。由于焦耳热可以与空气对流放出热量，因此可以将该模型设为稳态解。综上可以利用图3 所示的方程式进行求解。

微电阻梁在通电过程的热传递现象属于热传导问题，而热传导问题研究的是温度在空间的分布和随时间的变化，用T（x,y,z,t）表示。遵循基于傅里叶定律和能量守恒的热传导方程，其在笛卡尔坐标系下的瞬态三维热传导控制方程为：

该式中的负号表示热量传递方向与温度升高的方向相反，相关参数如下：

ρ--研究对象的密度；

T--材料的瞬时温度；

t--热传导时间；

Cp---研究对象的比热容；

k--热传导系数；

u--对流项中的外场因变量；

Q--热流密度，即研究对象所吸收的热量。

影响通电传热的因素众多，其实际物理过程也十分复杂，因此在对其进行温度场模拟时做出如下假设。

（1）假设微电阻梁模型材料为连续且各向同性。

（2）热量作用于模型内部的吸收率恒定，不随时间变化。

（3）不考虑材料表面受热变形的影响。

（4）模型间为完全热传导。

在模拟中使用以下边界条件和初始条件。

式中Γ 为边界条件，T为已知边界上的温度；n为模型边界外法线方向；q为材料表面单位面积的热流密度；h为模型与空气介质的对流换热系数；σ为玻尔兹曼系数；ε为模型材料的辐射率；Tf为初始温度，模型初始温度为25 ℃[9]。

3 计算结果

点击计算结果后，即可得出结果如下：

（1）表面温度分布图

如图4 显示，在使用方程1 中与温度相关的电阻率求解模型时微梁表面的温度场。根据颜色标尺，最高温度约为710 K。

（2）表面应力分布图

图5 显示了微梁的变形。与温度相关的情况下，位移为48 nm，而电导率恒定时，最大位移为88 nm（绘图将变形放大了约20 倍）。

4 仿真分析与讨论

本研究的仿真模型涉及电流的产生及满足电流守恒，需要用到电流守恒方程。电流产生的焦耳热需要向空气中对流，从而需要热传导方程。温度带来电阻率的变化，所以首先会用到传热和电流的双向耦合。同时，温度的提高引起材料的热膨胀，从而需要考虑固体力学中的热应变问题。所以需要电流，固体传热及固体力学三个物理场的耦合。在Comsol软件中，需要用到传热--电磁热下面的焦耳热及结构力学中的固体力学这两个物理场模块的耦合。由于焦耳热可以与空气对流进行散热，所以此模型可以建为稳态求解的方式。

由于电流在悬臂梁底端从一侧流向另外一侧，可以把悬臂梁的底端分别设为电流边界中的接地（电势为零）和终端（电势设为0.2 V）两个边界。传热边界：由于梁是在开放环境中工作，生成的热会消散到空气中，所以传热边界（即热通量）为除了底部的两个界面的其他表面，如图4 所示，其与空气的对流热通量设为5 W/(m2K)。底部的两个边界可以设为温度293 K。由于在热膨胀过程中，悬梁底部是被固定的，可以认为不发生变形，设为固体力学中的固定约束边界[10]。

5 结论

本研究通过对微电阻梁施加电流使其产生焦耳热，探究在热的作用下微电阻梁产生热应力发生的变形情况。计算了电阻率的电势分布，温度分布以及所受的应力分布的情形。此模型涉及电学、传热学、固体力学等相关知识的仿真模拟，对相关电阻传热研究具有一定的指导意义，为了研究微电阻梁的热损伤机理提供了一定的理论指导，为研究微电阻梁制作器件提供参考。