光电自准直经纬仪水平角测量误差分析

李永刚，姜苏洋，冯伟利，刘 岩，王占涛，王 蕾

（1.北京航天计量测试技术研究所，北京 100076；2.火箭军装备部驻北京地区第一军事代表室，北京 100076）

1 引 言

随着科学技术尤其是电子技术和计算机技术的发展，惯性导航、制导和控制有了较快的发展，精度越来越高。激光陀螺、光纤陀螺等光学捷联惯导系统已达到较高的精度，并在航空、航天和船舶领域得到广泛应用。

为保证各种应用需求，对惯导系统的姿态精度进行测量、标定和校准，需要利用高精度光电自准直经纬仪，实现高精度姿态的传递和测量校准。

光电自准直经纬仪采用光学自准直的基本原理，基于传统电子经纬仪基本结构形式，在横轴和竖直轴上分别安装电机和测角码盘。在望远镜的准直光路上折转分出光电自准直光路，增加准直光源、准直分化板和光电传感器等部分，以及相应的光电信号处理电路，形成光电自准直组件，从而组成新型光电自准直经纬仪。

在利用光电自准直经纬仪对惯性系统进行姿态测量时，一般进行相对角度测量，最主要的指标是水平角测量精度，要求光电自准直经纬仪具有较高的水平角测量精度。作为复杂的光电测量设备，光电自准直经纬仪水平角测量精度受多种因素的影响，本文将通过分析光电自准直经纬仪的结构形式、系统组成、测量原理，对影响光电自准直经纬仪水平角测量误差的因素进行逐项分析，对于其中的系统误差提出补偿方法。

2 光电自准直经纬仪系统组成

光电自准直经纬仪组成如图1所示。

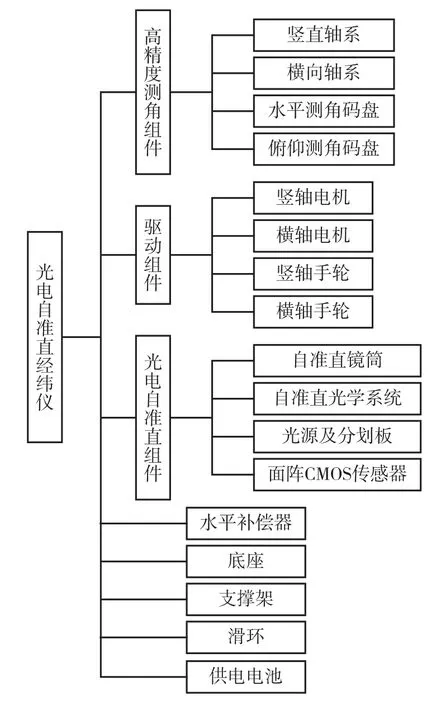
图1 光电自准直经纬仪组成Fig.1 Buildup of the photoelectric autocollimatic theodolite

光电自准直经纬仪为三轴地平结构形式。分别为竖直轴、横向轴、准直轴。其中竖直轴处于竖直状态，横向轴和准直轴绕竖直轴在水平面内旋转；准直轴与横向轴垂直，绕横向轴在竖直面旋转。

从功能上，光电自准直经纬仪可分为高精度测角组件、驱动组件、光电自准直组件、水平补偿器、底座、支撑架、滑环、供电电池等部分组成。

高精度测角组件由竖直轴系、横向轴系、水平测角码盘和俯仰测角码盘等组成，用于水平角和俯仰角全圆周角度的测量；准直轴绕竖直轴旋转的角度，由安装在竖直轴上的水平测角码盘给出，准直轴绕横向轴旋转的角度，由安装在横向轴上的俯仰测角码盘给出。

驱动组件由竖轴电机、横轴电机、竖轴手轮、俯仰手轮等组成，操作员旋转竖轴手轮，手轮内部计数码盘通过脉冲进行计数，竖轴电机根据脉冲数转动相应的角度，驱动竖直轴转动；操作员转动俯仰手轮，根据相同原理，横轴电机驱动横向轴转动。

光电自准直组件由自准直镜筒、光学系统、光源及分划板和面阵CMOS传感器等组成，用于二维小角度自准直测量。光电自准直组件对被测目标进行准直，对被测目标镜失准角通过面阵CMOS传感器将返回影像的偏移量转换为角度值。

在一次水平角测量过程中，高精度测角组件输出的角度值与光电自准直组件输出的角度值综合，再依据水平补偿器输出的倾斜量进行误差修正，即可获取投影到水平面的准确水平角。

3 光电自准直经纬仪水平角测量误差分析

根据光电自准直经纬仪的测量原理和系统组成，光电自准直经纬仪的误差影响因素主要包括高精度测角组件的测量误差、光电自准直组件测量误差和水平补偿器测量误差等。

3.1 高精度测角组件引入的测量误差

高精度测角组件的工作原理：在编码盘的码道上方安置一个发光源，在编码盘的下方正对发光源的位置安放一光电接收器件，当发光源照射到由透光和不透光部分构成的编码上时，会在光电接收器件上形成相应的图形并产生电压输出或零信号，即二进制的逻辑“1”或逻辑“0”，再经由数据处理系统转换为需要的角度信息，测角码盘测量原理如图2所示。

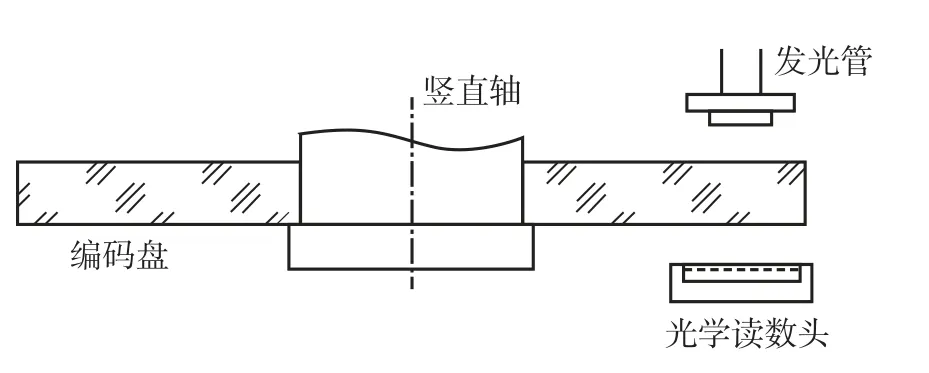
图2 测角码盘测量原理示意图Fig.2 Theory of the angle encoder

高精度测角组件的测量误差主要包括码盘刻线误差、码盘偏心误差、读数头细分误差、轴系误差等因素组成。

在水平角测量过程中，测角码盘工作时，编码盘随竖直轴旋转，发光管发出的光经编码盘照射到光学读数头上，光学读数头产生的光电信号实时给到编码器处理电路，处理电路将光电信号处理成数字信号，进而换算为角度信息输出。

根据测角码盘的测量原理，测角码盘是用刻线来标记码盘的位置，并表示光电自准直组件转过的角度，这些刻线与理论位置不一致而产生的误差称为分划误差，它是影响经纬仪测角精度最关键的因素，码盘刻划误差决定了测角精度能够达到的上限。例如，整个测角码盘的圆环区域内一般均匀的刻划有2048个条码，测角码盘的母盘采用光刻的制造方式制造，码盘采用曝光复制的形式制造。光刻误差依据光刻厂家能力，位置精度可以达到30 nm～300 nm不等。复制曝光前的匀胶、烘烤工艺，以及复制曝光工艺，曝光后的显影、蚀刻工艺，也都对精度有很大的影响，码盘刻划引入的测量误差计算公式为

式中：Δ——码盘刻划引入的测量误差；a——码盘刻划位置精度；R——码盘有效半径。

此项为测角码盘主要误差，若直接采用母盘作为测角码盘可以避免复制曝光、显影、蚀刻带来的误差。通过检测，激光直写码盘的刻线误差可以达到130 nm以内，在将测角码盘的有效直径做到72 mm，取a＝130 nm，R＝36 mm，代入公式（1）。

Δ＝360 0×arcsin（1.3×10／36）／2＝0.38″

则码盘刻划误差引入的测量误差为0.38″。

当码盘的刻度中心与旋转轴旋转中心不重合时，即当码盘偏心旋转时，单个读数头读数测角会产生很大的角度测量误差。对于有效直径72 mm的码盘，偏心0.01 mm可产生57″的测角误差。偏心引起的测量误差为系统误差，为了提高测角精度，必须采取措施将偏心引入的测量误差加以消除，码盘偏心示意图如图3所示。

图3 码盘偏心示意图Fig.3 Eccentricity of the encoder

根据偏心误差产生的机理，当采用2个对径安装的光学读数头读数取均后，可以极好地消除此偏心误差。但误差消除效果取决于光学读数头对径安装精度。当光学读数头相对于旋转中心完全按按照180°对径安装时，可以将偏心误差完全消除。对于现有产品，光学读数头安装固定为螺丝孔对位安装，可以将对径安装误差控制在±0.5°范围内，采用4个光学读数头间隔90°均布安装，即可将偏心误差标准偏差消除至0.08″以内。同时将光学读数头安装方式更改为轴位螺钉固定，采用读数显微镜测量光栅盘基圆线，测得光栅盘偏心，与压紧光栅盘比对后可以调整光栅盘偏心误差至0.01 mm以内，再点胶固化，固化完成后再以读数显微镜复核偏心误差，确保仍在0.01 mm以内，实测控制数据见表1。

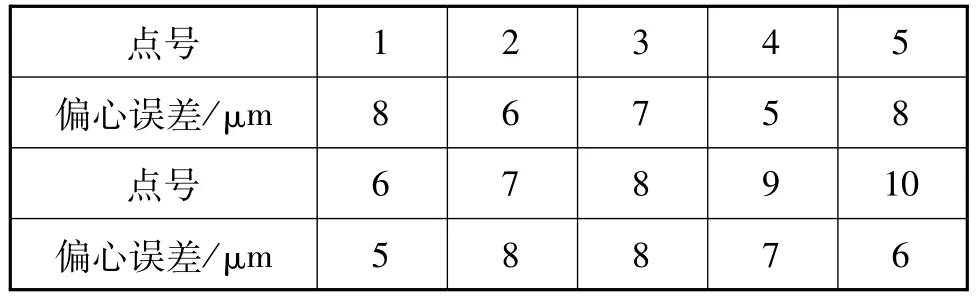
表1 偏心误差实测值Tab.1 Measured value of the eccentric error

采用销子螺钉定位，机械行业内，常规螺钉与螺纹孔间隙为0.15 mm，对应到光学读数头对径安装误差是β＝arctan（0.15／35.5）＝0.24°。控制光学读数头对径安装误差在β＝0.3°以内，进而将偏心引起的测量误差控制在0.1″以内，达到可以忽略的水平，计算公式为

式中：δ——对径安装的第一个读数头偏心引入的测角误差；e——偏心值；θ——旋转角度值。

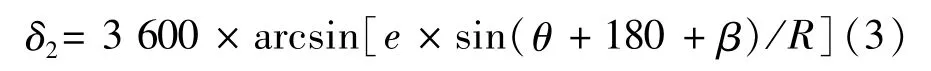
式中：δ——对径安装的第二个读数头偏心引入的测角误差；β——两读数头对径安装角度偏差。

式中：Δ——对径安装的两个读数头偏心引入的水平测角误差。

取e＝0.01 mm，R＝36 mm，β＝0.3°，θ＝0～360°，分别代入公式（2）（3）（4）可以得到

测角码盘采用单码道环形伪随机编码，360°范围共有2 048条码，码盘有效半径R＝36 mm，采集条码的光学读数头传感器为模拟量线性CMOS传感器，单像素大小为8μm×125μm，模数转换芯片为10位ADC，那么测角模块理论所达到的最高分辨率为

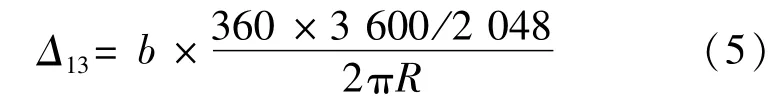
式中：b——单像素尺寸；R——码盘有效半径。

根据码盘有效半径R＝36 mm，单像素大小一般为b＝7.8μm，模数转换芯片采用10位ADC，将以上参数代入公式（5），那么测角码盘理论所达到的读数头细分误差计算得到

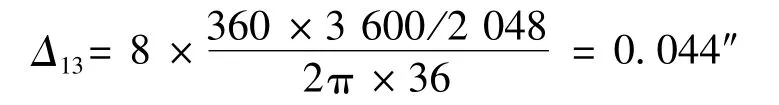
3.1.4 轴系误差引入的测量误差

为保证旋转精度消除游隙，轴系采用密珠轴系，轴的圆度小于等于0.3μm，粗糙度≤R a 0.1；横轴密珠80颗，竖直轴密珠208颗，滚珠和轴系间采用过盈配合，使得每个密珠都能按照规律方向转动。对于轴系产生的误差，直接测量比较困难，但装上码盘后的综合误差很容易体现。

对于密珠轴系这类消除了游隙的旋转系统，轴承在任意位置均不会存在晃动。旋转误差的主要体现在于旋转时码盘的偏心跳动和端面跳动。对于偏心跳动，可以控制其在2μm范围内并通过对径安装光学读数头消除。而对于端面跳动，通过提高加工精度可以保证轴承装盘后码盘端面跳动在2μm以内。以千分表测量码盘端面跳动，测量结果见表2。

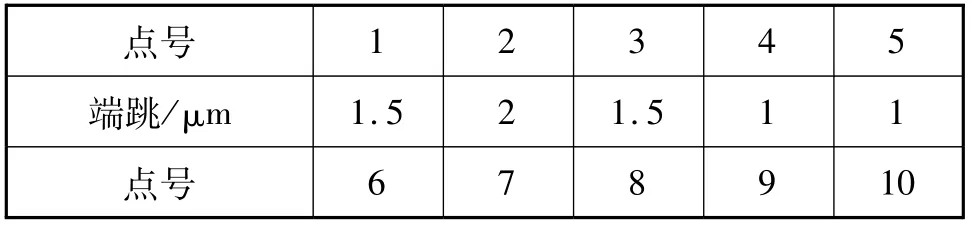
表2 密珠轴系端面跳动实测值Tab 2 Lateral runout measured value of the dense bead shafting

端面跳动在测量面上的投影为

由端面跳动引起的测量误差为：

根据端跳误差e＝0.002 mm，R＝36 mm，代入公式（6）、（7），计算获得端跳引起的测量误差为

以上各误差因素相互独立，高精度测角组件的水平角综合测量误差计算公式为

在公式（8）中代入各个误差分量，高精度测角组件的水平角测量误差为

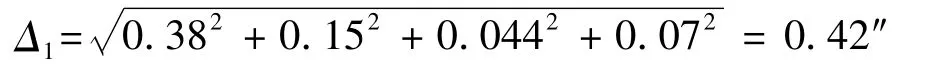
3.2 光电自准直组件测量误差

光电自准直组件是基于光学自准直仪的原理发展而来的，光电自准直组件将被测目标镜返回图像的光学信号，利用光电转换器件进行图像处理，转换为位置信息。光电自准直测量光学系统如图4所示。

图4 光电自准直测量光学系统示意图Fig.4 Optical system of the photoelectric autocollimator

光源照亮带十字刻线的准直分划板，分化板亮线经过反射镜一反射至分光镜二，经过分光镜二透射、物镜组折射后形成平行光，并照到目标镜上，目标镜反射回的亮线再经过物镜组、分光镜一，当反射亮线经过分光镜一时，一部分光透射经过分光镜二透射、调焦镜一折射、正像镜，成像在目视分划板上，另一部分光经过分光镜一反射、调焦镜二折射、反射镜二反射，汇聚到CMOS传感器上。

如果目标镜与光轴垂直，自准直亮线与目视分划板刻线重合，如果反射镜与光轴不垂直，即反射镜倾斜一个角度，根据反射光的倾斜程度，自准直亮线会以相应的角度发生位移，在目视分划板和CMOS传感器上成像，通过对CMOS传感器上的图像信号进行处理，算出自准直亮线相对目镜分划板十字丝在X方向与Y方向的相对位移量，根据相对位移量换算成角度值，可计算出反射镜倾斜的角度值。

光电自准直组件精度对整机精度起着重要作用，其测量误差主要来源于角度标定基准误差、质心定位误差、光学系统误差、光束不平行度引起的测量误差等因素。

光电自准直组件的精度标定选用激光小角度测量装置作为标准实现。激光小角度标准装置是利用激光干涉法进行小角度测量，是小角度参数国防最高计量标准器具，在±1°范围内的静态测量精度可达δ＝0.03″。

因此，利用激光小角度标准装置进行精度标定，由该角度标准引起的测量误差

Δ＝δ＝0.03″

为了提高测量精度，光电自准直组件选择高分辨率图像传感器，单个像元尺寸为d×d（5.5μm×5.5μm）。采用质心定位算法，可实现1／20像素级质心定位精度细分，准直光学系统焦距f为300 mm。依据光电自准直测量原理，质心定位算法引入的测量误差分量为

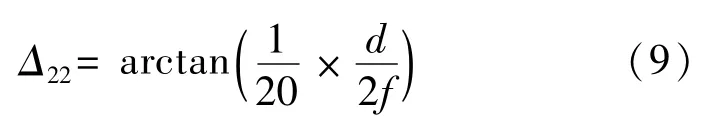
将像元尺寸d，焦距f代入公式（9）计算，得到

Δ＝0.09″

对光学系统的要求是要保证光学系统中像点偏移要小，并且畸变应得到很好的矫正。

为了提高设备的测量精度，需要设计性能优良的准直光学系统。通过光学设计软件CODE V分析，在全量程范围内，光学像差引起的最大质心偏移量为

δ＝2.6×10mm

依据光电自准直测量原理，质心偏移量则引起的测量误差公式为

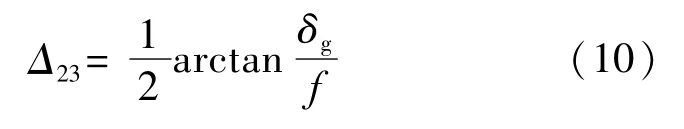
将质心偏移量δ，焦距f代入公式（10）计算，可得

Δ＝0.09″

光电自准直组件采用高均匀性照明光源和平行光控制技术实现光束平行度控制，依据设计的光学系统，全视场最大弥散斑半径为2.03μm，计算出的射光不平行度Δθ为

若出射光束不平行，则存在Δθ的会聚角（或发散角，符号相反），如图5所示，光束将在有限距离l处A点会聚，经被测反射镜反射后成像于A′点，此时A′点距离准直光学系统入瞳距离为l－2d，A′点经准直光学系统后成像在A″。

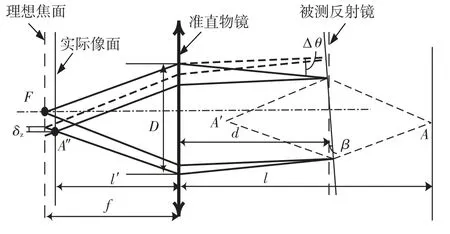
图5 光束不平行引入测量误差示意图Fig.5 Measurement error caused by beam non parallel

则根据几何光学原理可得实际像面距离l′为

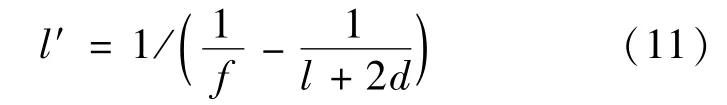
式中：l′——实际像面距离；d——测量距离。

将f＝300 mm，Δθ＝1.4″，d＝5 m等参数代入公式（11），两极端测量距离下实际像面位置l′计算得到

则光束不平行度引起的质心偏移量δ，计算公式为

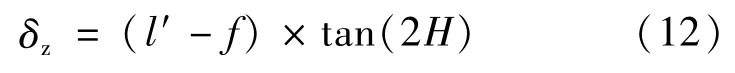
式中：δ——光束不平行度引起的质心偏移量；H——光电自准直仪量程，H＝2 000″。

代入以上参数，计算得到

δ＝2.1×10mm

则由于光束不平度引起的测量误差计算公式为

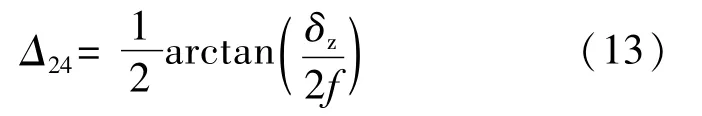
将质心偏移量δ、焦距f代入公式（13），计算得到

Δ＝0.065″

在使用光电自准直经纬仪进行水平角测量过程中，常常会有倾斜瞄准测量的情况，在倾斜状态下，水平测角码盘保持水平不变，其测量的水平角直接代表光电自准直组件在水平面内转动的角度，对于自准直测量，自准直角度是在倾斜面内产生的，为了准确表达水平角，需要将自准直角度投影到水平面内。

如图6所示，在经纬仪测量过程中，OXM面为经纬仪水平面，假设P点为被测目标点，光电自准直组件的仰角为θ时，自准直测量角度值为α′，此时的α′值为倾斜OP方向的角度值，投影到水平面内的角度为α，那么

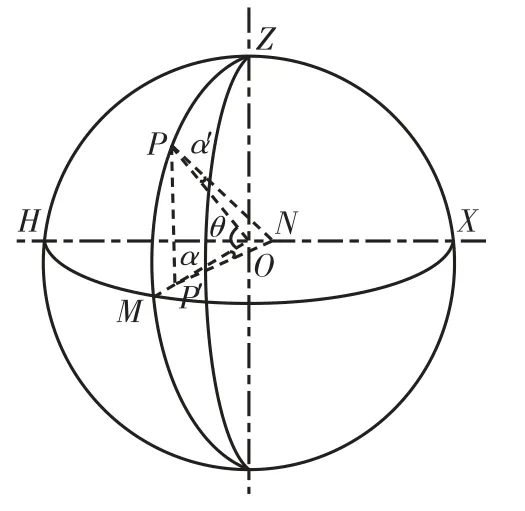
图6 自准直测量倾斜补偿示意图Fig.6 Tilt compensation for autocollimation measurement

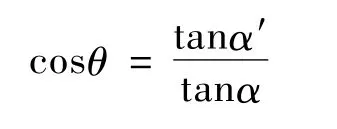
读取经纬仪的仰角值θ，光电自准直水平角测量值，可以计算水平面内的自准直角度值α为

α＝arctan（tanα′／cosθ）

由于自准直测量角度值为小量，上式可以简化为：

由公式（14）可见，α值越大，α′值与α值的差异越大。另外，θ值越大，α′值与α值的差异越大。实际应用中，自准直测量范围为（－300″～300″），俯仰角最大可达40°，根据已知α，有必要通过公式（14）进行校正。

以上各误差因素相互独立，光电自准直组件的水平角测量误差计算公式为

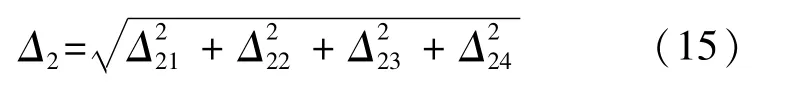
在公式（15）中代入各个误差分量，光电自准直组件的水平角测量误差为

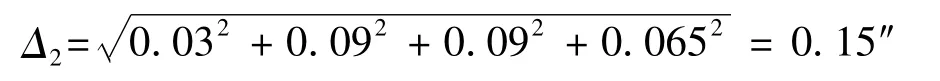
3.3 水平补偿器引入的测量误差

光电自准直经纬仪配有水平补偿器，水平补偿器与竖直轴安装在一起水平补偿器测量竖直轴垂直度，根据倾斜量对水平角测量码盘测角量进行补偿，通过标定，水平测量误差不大于3″，水平补偿器水平测量误差θ＝3″。

如图7所示，OO′为竖直轴，OPQ为水平面，O′PQ为倾斜面，倾斜面O′PQ相对水平面OPQ的倾斜角度误差为θ；水平角测量码盘测量角度值为α′＝∠PO′Q，投影到水平面内，水平角测量角度值为α＝∠POQ，根据图7的几何关系，各角度的关系为

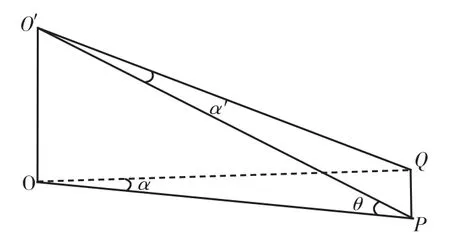
图7 水平测角码盘倾斜测量示意图Fig.7 Tilt measurement of horizontal angle encoder

即

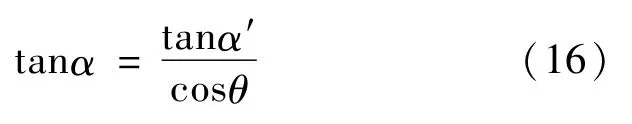
倾斜引起的测量误差为

δ＝α′－α

那么

将公式（16）代入公式（17），即有

依据三角公式

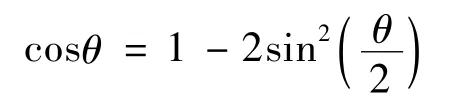
代入上式，即有

进一步简化为

由上式可见，水平补偿器带来的水平角测量误差，在不同的水平角范围，影响量不同，水平补偿误差在水平角α′＝40°进行测量时影响最大，将参数代入公式（18）计算，水平补偿误差带来的测量误差为

δ＝0.000 6″

可见，水平补偿器补偿误差3″时，对水平角传递的影响极小，可以忽略不计，说明水平补偿器的水平补偿精度能够满足高精度光电自准直经纬仪的要求。

水平补偿器零位误差是指水平补偿器零位的稳定性，一般在机械安装后通过软件置零，之后靠机械稳定性确保；长期使用过程中，由于应力影响可能会有变化，可以通过旋转竖直轴在水平面全圆周4个均布角度下查看其零位稳定情况，通过软件进行置零。通过试验，水平补偿器零位误差可控制在5″以内。

水平补偿零位误差带来的水平角测量的影响，与水平补偿误差原理相同，根据公式（15），在不同的水平角范围，影响不同，通过分析，水平补偿误差在水平角进行40°角测量时影响最大，影响因素为：

δ＝0.001 7″

可见，水平补偿器零位误差5″，对水平角传递的影响极小，可以忽略不计，说明水平补偿起零位稳定性能够满足光电自准直经纬仪测量精度要求。

3.4 光电自准直经纬仪水平角综合测量误差

根据以上分析，影响光电自准直经纬仪水平角测量误差的因素包括高精度测角组件测量误差和光电自准直组件测量误差，以上各误差因素相互独立，光电自准直组件的水平角测量误差计算公式为

在公式（19）中代入各误差分量，光电自准直经纬仪的水平角综合测量误差为

4 结束语

本文简要介绍了光电自准直经纬仪的系统组成和测量原理。依据测量原理全面分析了对光电自准直经纬仪水平角测量精度影响的各个误差分量，对光电自准直经纬仪各组件测量误差进行了定量计算，对于系统误差提出修正补偿方法。通过定量分析，对各测量组件的相应误差分量进行误差控制，光电自准直经纬仪能够达到0.5″的水平角测量精度，满足Ⅰ等电子经纬仪的测量精度指标。利用本文提出的误差分析方法还可以对其它光电类测量仪器进行分析，可以较好地控制研制生产过程质量和设备精度，具有广泛的推广应用前景。