一种顾及厄特沃思效应的水下重力辅助导航方法

张光俊，张梦得，张忠侠，高端阳

（1.中国人民解放军92941部队，葫芦岛 125000；2.中国人民解放军92330部队，青岛 266000；3.中国人民解放军91917部队，北京 100036；4.海军工程大学导航工程系，武汉 430033）

1 引 言

在水下环境中卫星导航系统无法正常工作，惯性导航系统成为了更为主流的导航方式，并得到了广泛应用。鉴于惯性导航系统误差随时间积累这一固有弊端，纯惯性导航方式难以实现水下长航时的导航需求，必须通过其他辅助信息源对惯性导航系统进行定期校正，以抑制惯性导航系统的误差积累效应。通过船底搭载计程仪可以测量得到潜航器相对地面的航行速度，利用该速度信息可实现对惯导速度误差的定期修正。但是惯导／计程仪这种组合模式依然没有逃离惯导积分定位原理的本质，长航时位置信息依然存在误差积累，只是在误差积累的快速性上起到了一定的缓解作用。水下声学定位系统也是一种外界辅助信息，但是该系统需要布置基站，建设和维护工作较为困难，成本较高，也难以实现全海域辅助导航定位。海洋物理场作为地球的本质属性，一是不受空间地域的限制，可实现全海域辅助导航定位的需求，二是基于海洋物理场的匹配导航方式，可实现对惯导位置误差定期校正，有效解决惯导位置误差发散问题。鉴于上述优点，加之近年来超导技术和原子干涉技术等前沿技术在重力精密测量领域的应用，重力测量精度逐步提高，重力仪器环境适应能力逐步增强，基于重力匹配的辅助导航方式得到了越来越多学者的关注。

重力测量、重力参考图和重力匹配算法是构成重力匹配导航系统的三个关键部分。本文重点关注重力匹配算法领域的研究。ICCP、TERCOM 和SITAN是当前最为经典的三种重力匹配算法，针对以上三种传统算法的不足，文献［10－12］对ICCP匹配算法进行了改进，文献［13，14］对TERCOM匹配算法进行了改进，文献［15－17］对SITAN匹配算法进行了改进，以增强算法的快速性或定位精度。但这三种算法的底层思想均源于地形匹配导航研究领域，重力信息与惯性导航系统信息融合不够紧密。卡尔曼滤波和粒子滤波等算法通过建立系统模型，为惯性信息与其他辅助信息源的有效融合提供了手段。文献［10，18，19］对基于粒子滤波、质子滤波算法的重力匹配算法进行了较为深入的研究，无论是粒子滤波还是质子滤波都存在计算量较大的问题，难以实现实时重力辅助导航。文献［20，21］提出了采用UKF的非线性滤波框架实现重力匹配，相较于粒子滤波算法减少了计算量。

重力仪随水下运载体与地球产生相对运动，进而产生科里奥利力作用于重力仪，使得重力测量值发生变化，这种现象称为厄特沃思效应。厄特沃思效应与水下载体的位置和速度信息有关，特殊情况下厄特沃思效应可达上百厄特沃思，成为了重力测量的关键误差源。厄特沃思校正是重力仪测量数据处理过程中的关键步骤，传统重力匹配算法研究大都建立在可获得精确重力信息基础上展开的，但是对于水下应用环境，重力仪无法利用卫星导航系统提供的导航参数进行厄特沃思校正，厄特沃思估计误差势必影响重力仪的测量精度，进而影响重力辅助导航精度。本文顾及厄特沃思效应的影响，构建了水下INS／计程仪／重力仪组合导航框架，采用了UKF非线性滤波算法进行信息融合，通过半物理仿真分析了不同导航模式下厄特沃思估计误差特性，以及厄特沃思估计误差的存在对重力辅助导航性能的影响。

2 重力测量与数据处理

2.1 运动加速度方程

本文讨论的背景是海洋绝对重力仪。绝对重力仪不仅测量重力加速度，还测量载体的运动加速度以及由于地球自转（厄特沃思效应）耦合而产生的加速度。重力仪测得的加速度为

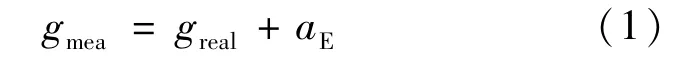
式中：g——海洋重力仪的测量绝对值；g——重力加速度真值；a——厄特沃思加速度。

因此，海洋绝对重力仪测量的原始数据需要经过一定处理才能得到准确的、可用的重力信息，其中厄特沃思校正是数据处理最为关键的步骤。测量得到的绝对重力值减去地球正常重力场模型计算值，实现重力异常信号的提取。

2.2 厄特沃思效应及误差分析

厄特沃思效应计算公式为

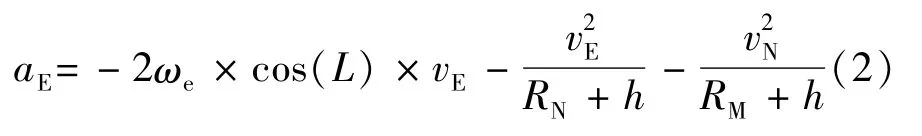
式中：ω——地球的自转角速度；L——纬度；h——高度；v和v——分别为东向速度和北向速度；R和R——分别为地球的本初垂直半径和地球在子午线的曲率半径。观察公式（2）可知，厄特沃思效应主要与载体的纬度和东向速度信息有关，下面分别分析纬度误差和东向速度误差对厄特沃思估计误差的影响。

当纬度误差为δL，速度项不存在误差时，则厄特沃思估计误差δa为

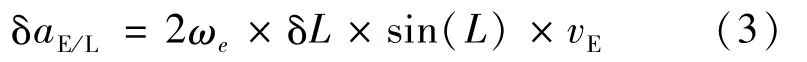
当东向速度误差为δv，纬度不存在误差时，则厄特沃思估计误差δa为：

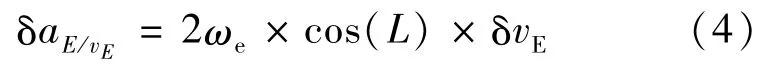
为了定量分析不同纬度误差和东向速度误差对厄特沃思效应的影响，假定水下航行器东向航行速度为5节，在纬度0°～90°范围内进行数值仿真分析，如图1所示。在中低纬度区域，0.1m／s的东向速度误差会产生1 mGal以上的厄特沃思估计误差，而纬度误差超过90 n mile时才会导致1 mGal厄特沃思估计误差如图2所示。因此，可认为重力仪动态测量精度对东向速度误差更为敏感。若要精确对厄特沃思效应进行补偿，需要外界提供较为精确的东向速度信息。

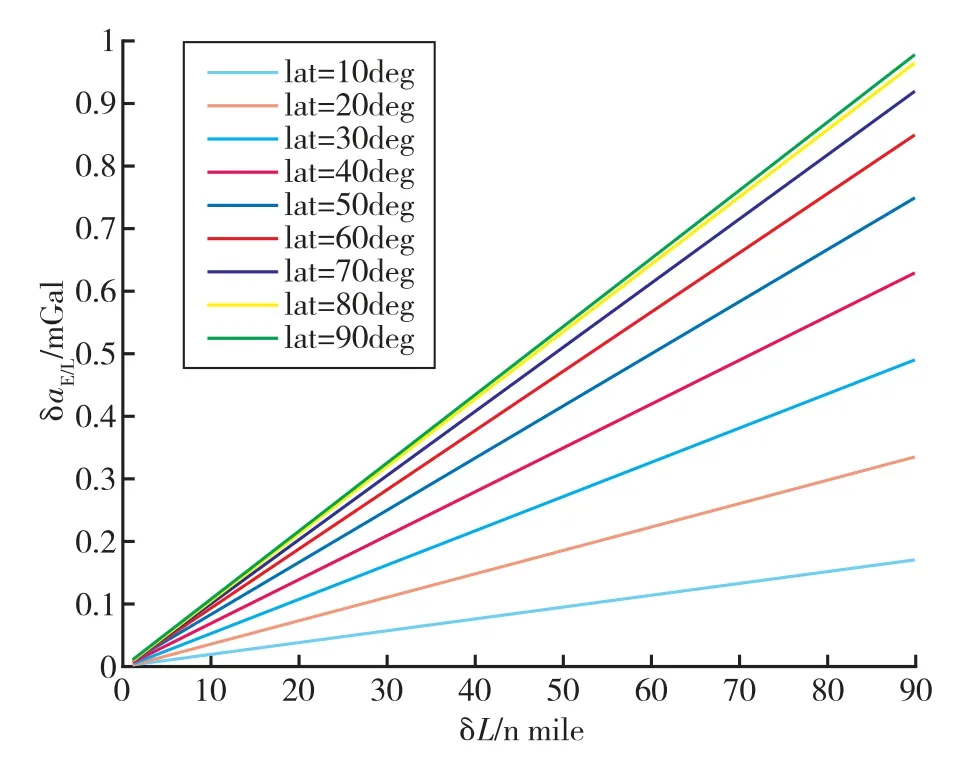
图1 纬度误差对厄特沃思效应的影响Fig.1 Relationship between latitude error and Eötvös estimation error

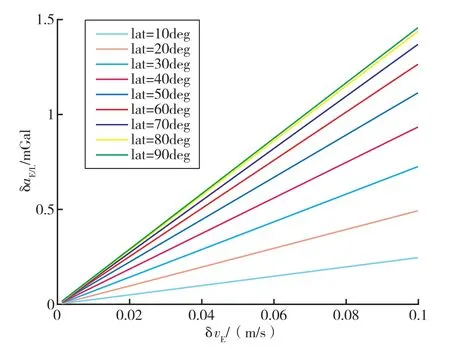
图2 东向速度误差对厄特沃思效应的影响Fig.2 Relationship between eastward velocity error and Eötvös estimation error

2.3 重力异常估计

重力异常通过WGS84正常重力模型减去重力测量值获得，同时考虑高度和纬度影响。正常重力计算公式为

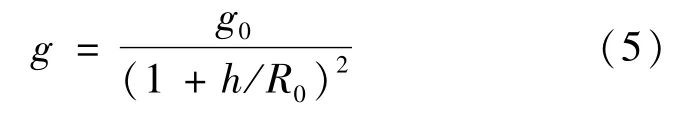
其中，

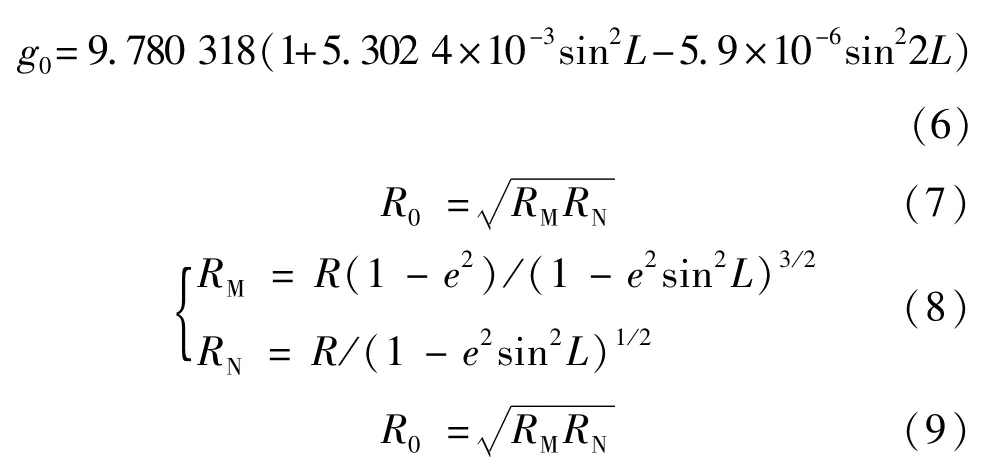
式中：g——考虑高度和纬度影响的重力加速度；g——赤道处海平面上的重力加速度；R——参考椭球的地球长半径，e——参考椭球的第一偏心率。

3 水下辅助导航的数学公式

水下惯性导航系统／计程仪／重力仪组合导航系统一方面可实现水下重力仪精确测量，另一方面可实现水下长航时导航定位，抑制惯性导航系统的误差积累，如图3所示。重力匹配问题是通过噪声观测来估计这种随机动力系统的状态（姿态、速度和位置），本研究中的噪声观测是指重力异常测量。

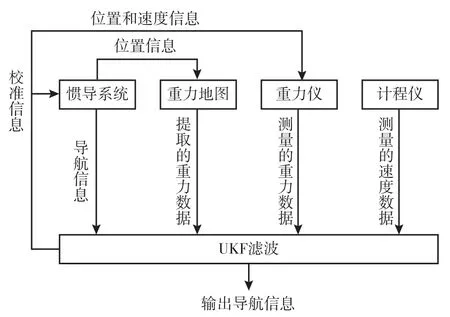
图3 水下组合导航框图Fig.3 Block diagram of underwater aided navigation

3.1 状态方程

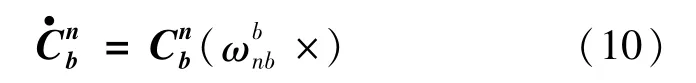
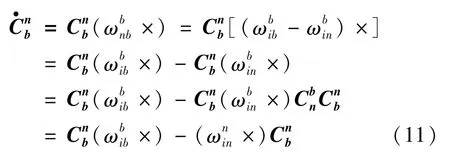
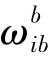
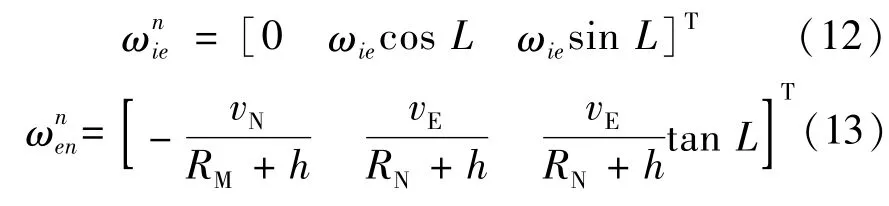
SINS在导航坐标系下的比力方程为

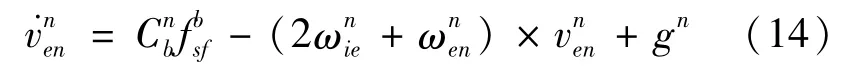
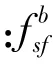
公式（14）表明，在从加速度计的输出中扣除有害加速度后，速度可以通过积分加速度得到，位置可以通过积分速度得到。因此，比力方程是SINS的基本方程。

导航坐标系下的位置微分方程为

本文将惯性导航系统的基本方程作为状态方程，水下航行器的姿态、速度和位置信息作为状态量。离散化动力学方程为

式中：x——k时的状态量，包含姿态、速度和位置；f——INS状态递推方程；w——离散过程噪声。随机噪声｛w｝是独立的零均值高斯白噪声，w协方差矩阵记为Q。

3.2 量测方程

在本文研究中，将计程仪测量的速度信息和重力仪测量的重力信息作为观测量。需要注意的是，计程仪测量的是b系下的速度，在使用的过程中需要经过坐标转换。观测矩阵构建为

量测方程为

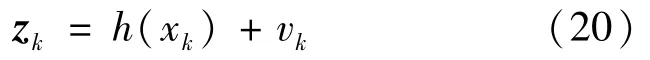
式中：z——k时刻重力异常量测量；h（x）——状态和测量之间的函数；v——量测误差。

3.3 UKF滤波算法

UKF是对非线性函数的概率密度分布进行近似，用一系列确定样本来逼近状态的后验概率密度，摒弃了对非线性函数进行线性化的传统方法。

(3)UAV+RFID的三维路径规划问题的首要任务为寻找从起始点到终点的最优路径，设置了路径最小适应度函数来求起始点和终点之间的最优路径。

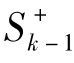
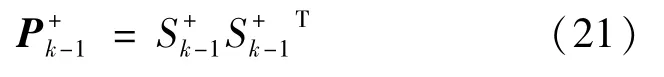
计算sigma点

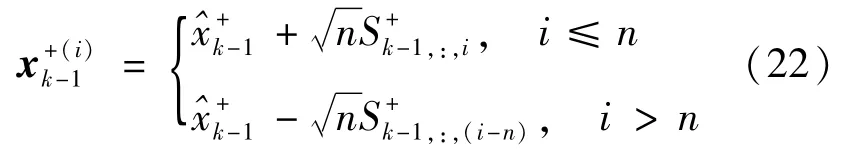
其中，下标“：，i”表示矩阵的第i列。每个sigma点都可以通过系统模型传播

状态估计及其误差协方差为

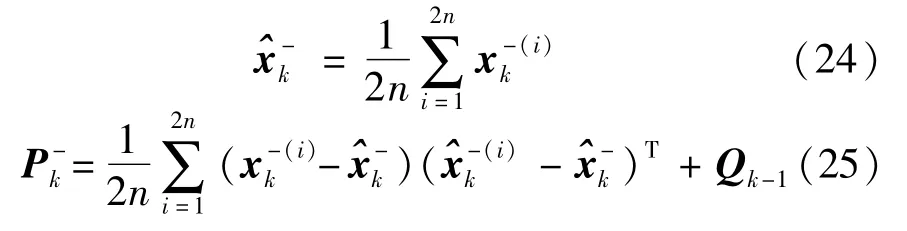
UKF的观测更新过程通过以下公式生成新sigma点

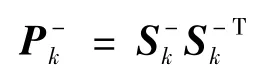
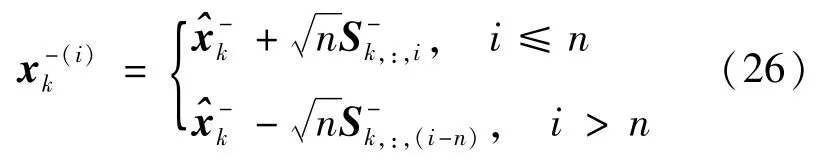
Sigma点和平均观测信息可通过以下公式求解

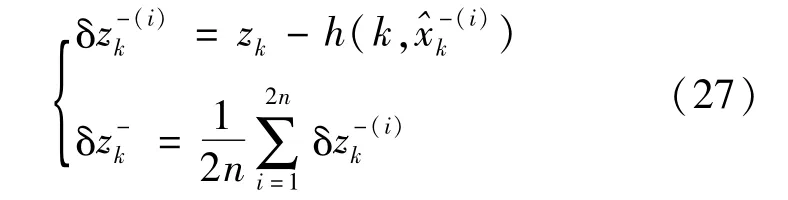
观测方程的新协方差为

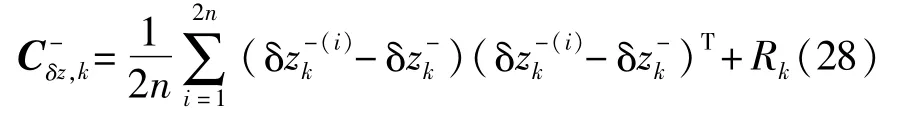
最后，UKF Kalman增益、状态向量更新和误差协方差更新计算方式为

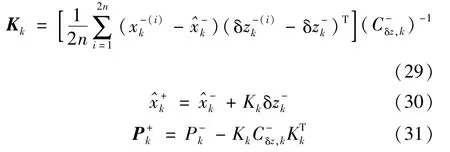
4 仿真结果与讨论

4.1 试验环境

为了评估算法的可行性，本文采用了一组约6 h船载实测数据进行验证。试验船搭载的IMU和DVL设备主要性能指标见表1和表2。试验船同时搭载了一个单天线的GPS接收机，以1 Hz频率输出速度和位置信息，并作为本次试验的速度和位置参考基准。

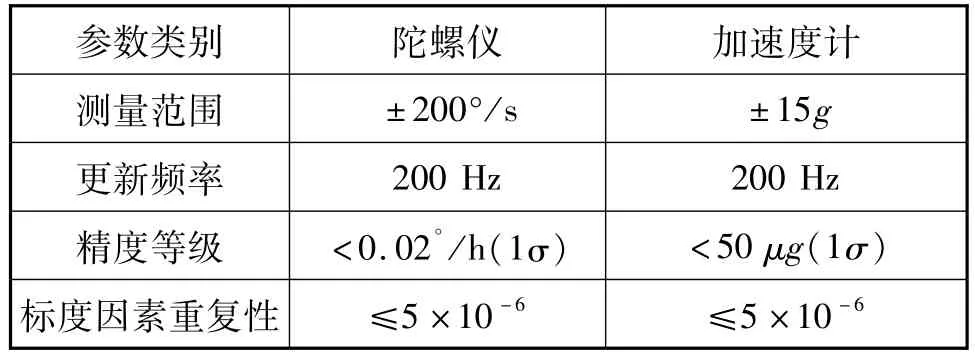
表1 IMU设备性能指标Tab.1 IMU performance indexes

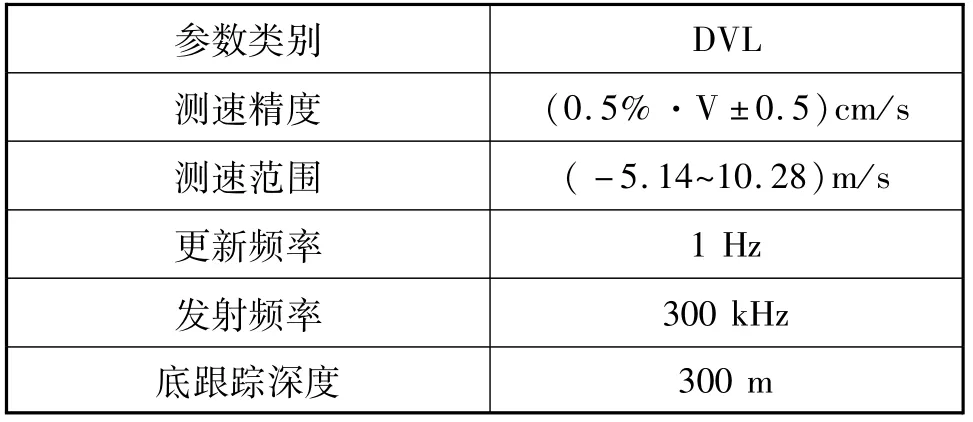
表2 DVL设备性能指标Tab.2 DVL performance indexes

在本文的半物理仿真实验中，使用最高阶的EIGEN－6C4球谐模型计算重力数据，并计算重力匹配图的分辨率，如图4～6所示。

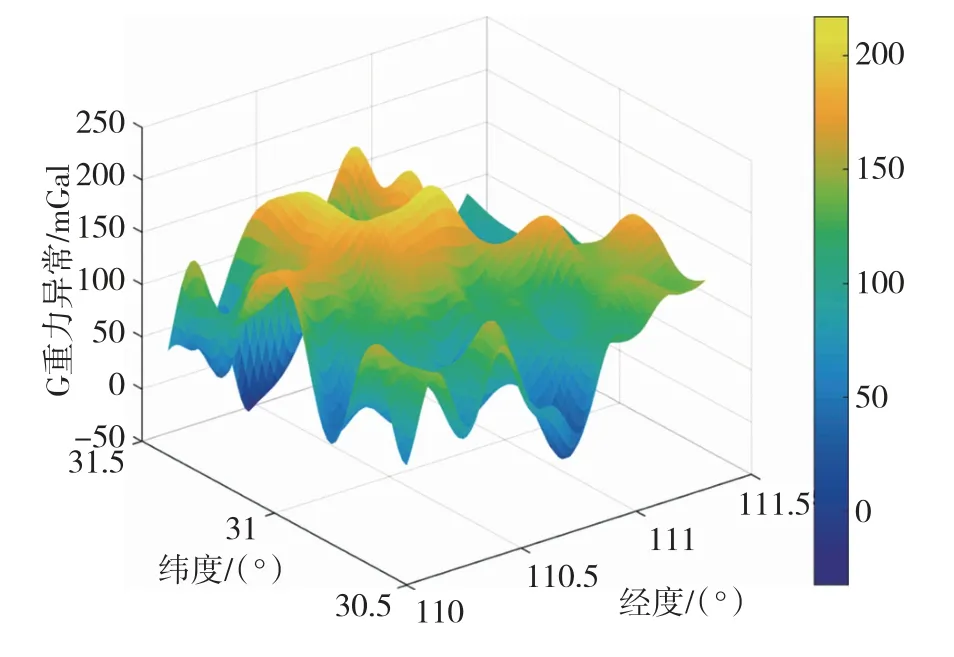
图4 匹配区重力异常三维图Fig.4 Gravity anomaly three-dimensional map in matching area

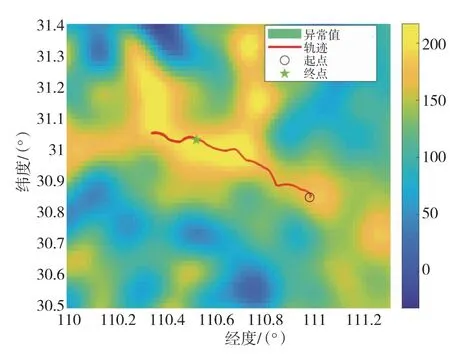
图5 匹配区重力异常二维图Fig.5 Gravity anomaly two-dimensional map in matching area

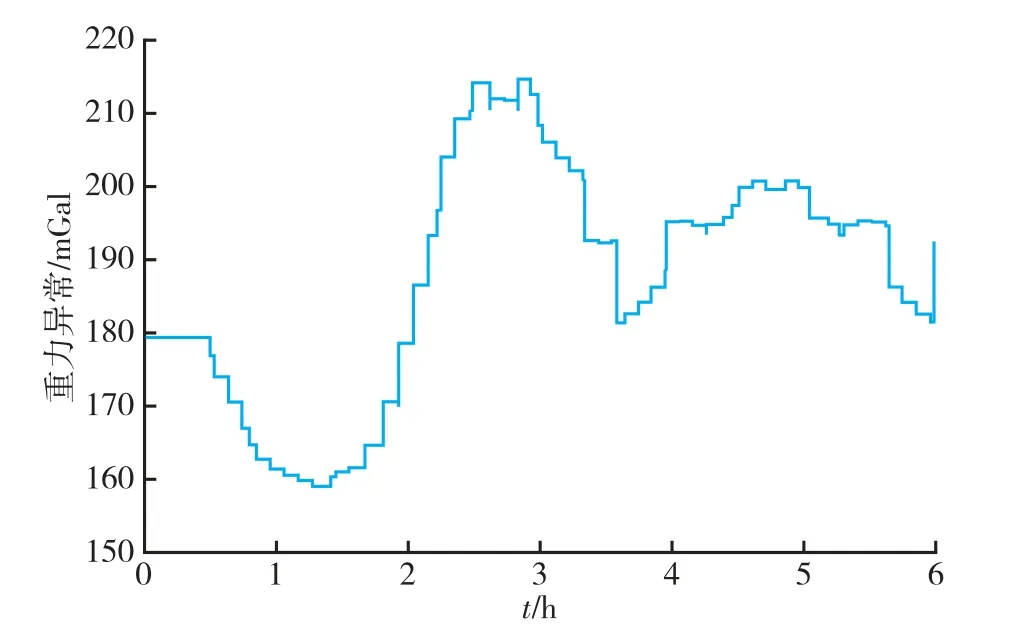
图6 重力异常变化曲线Fig.6 Variation curve of gravity anomaly on the track

4.2 结果与分析

将试验船处于系泊状态下前500 s的IMU数据采用优化对准方法进行惯导初始对准，并将初始对准的结果用于纯惯性推算，纯惯性推算的位置误差如图7所示。

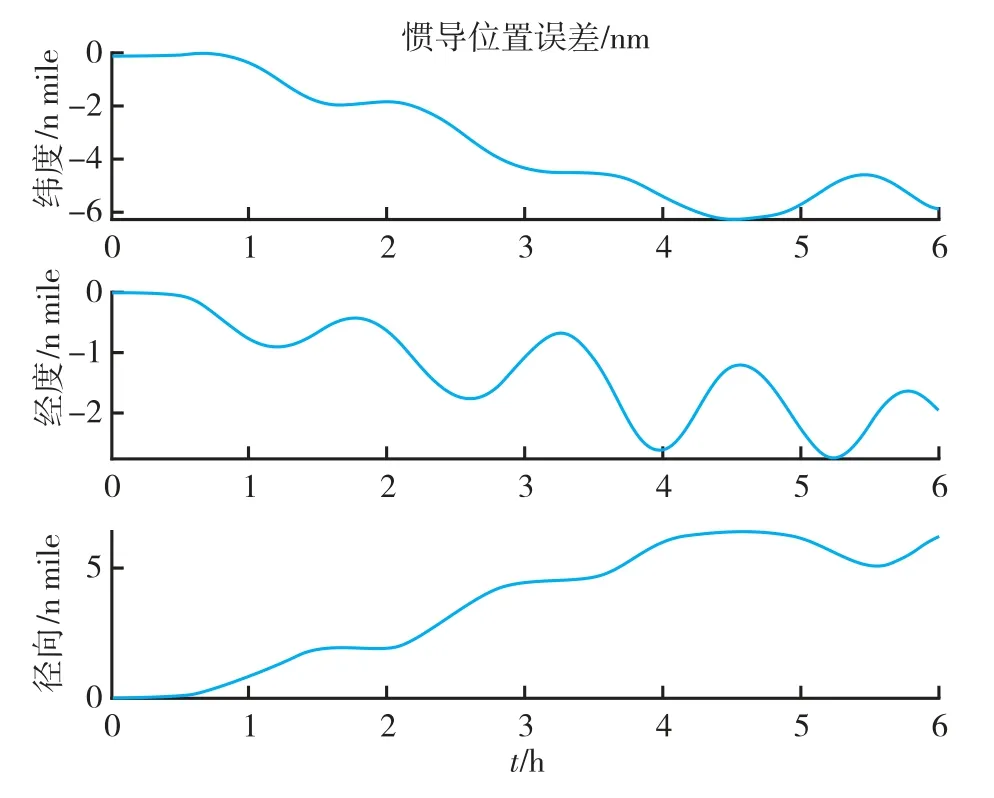
图7 纯惯性计算位置误差Fig.7 Pure inertial calculation position errors

厄特沃思估计精度是影响重力仪测量精度的关键因素，尤其是载体处于水下长航时航行状态，重力仪无法由卫星导航系统提供航行器精确的导航参数参与厄特沃思计算，其测量精度将会受到较大影响。重力匹配导航传统算法并未考虑厄特沃思效应对重力辅助导航系统性能的影响，都是建立在重力信息准确测量基础之上，未充分考虑重力仪辅助导航水下应用场景的特殊性。鉴于此，本文考虑了纯惯性推算（INS）、INS／DVL组合（INS／DVL）、不考虑厄特沃思校正的INS／DVL／重力仪组合（INS／DVL／Gravimeter）和考虑厄特沃思校正的INS／DVL／重力仪组合的四种导航模式。需要说明的是，不考虑厄特沃思校正的INS／DVL／重力仪组合模式，重力仪测量精度设置为1 mGal，考虑厄特沃思校正的INS／DVL／重力仪组合模式，重力仪测量精度为1 mGal的基础上叠加厄特沃思估计误差的影响。纯惯性推算结果如图7所示，其余三种导航模式位置误差曲线如图8～图10所示，四种导航模式最大误差统计如表3所示。

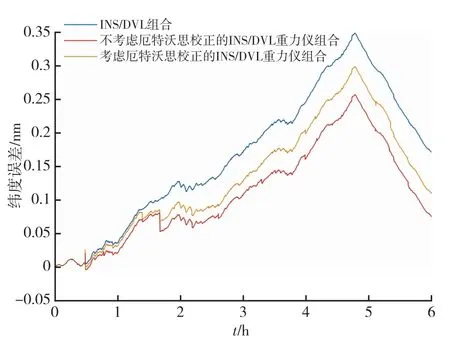
图8 纬度误差Fig.8 Latitude errors

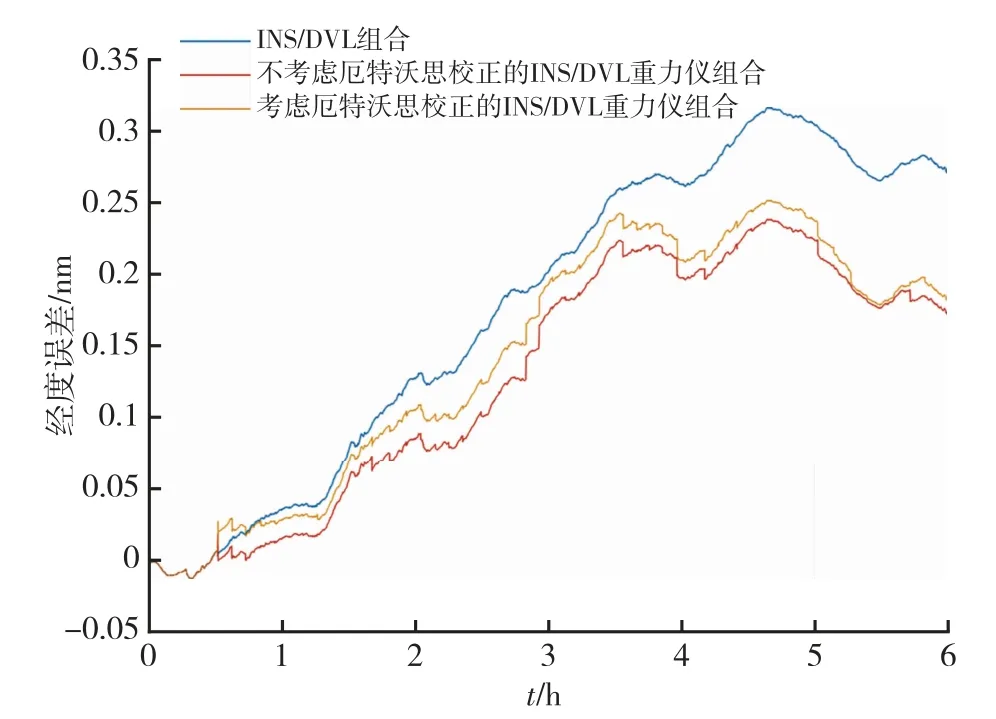
图9 经度误差Fig.9 Longitude errors

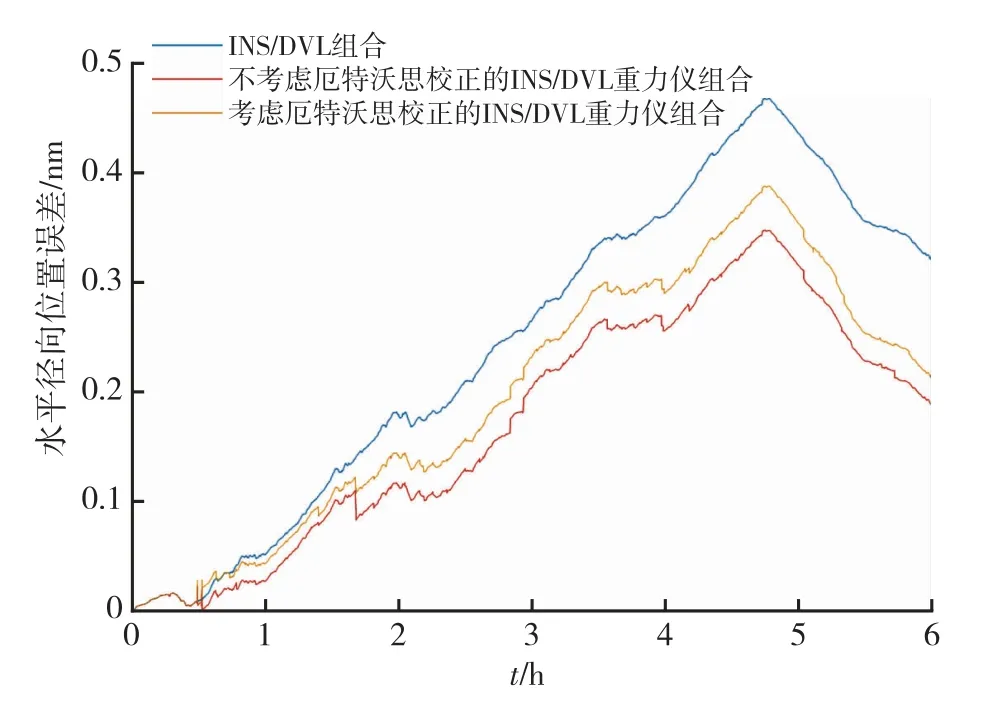
图10 水平径向位置误差Fig.10 Horizontal radial position errors

分析表3可知，6小时纯惯性推算纬度方向最大误差为6.28 n mile，经度方向最大误差为2.75 n mile，水平径向最大误差为6.39 n mile，可见在无任何外界辅助信息的情况下，惯性导航系统位置误差随时间快速积累。当采用DVL辅助惯性导航时，相比较于纯惯性导航，其定位性能得到了较大改善，DVL的辅助有效抑制了纯惯性推算位置误差快速发散问题。当采用DVL和重力仪共同辅助，不考虑厄特沃思估计误差时，纬度方向、经度方向和水平径向最大误差分别为0.26 n mile，0.24 n mile和0.35 n mile，在仅采用DVL作为辅助信息源相比，在三个方向上定位性能分别提升了25.71%，25% 和25.53%。考虑厄特沃思估计误差时，纬度方向、经度方向和水平径向最大误差分别为0.30 n mile，0.25 n mile和0.39 n mile，与仅采用DVL作为辅助导航模式相比，在三个方向上定位性能分别提升了14.29%，21.88%和17.02%。因此，重力仪的参与，即使考虑厄特沃思效应，定位性能也得到了提升。

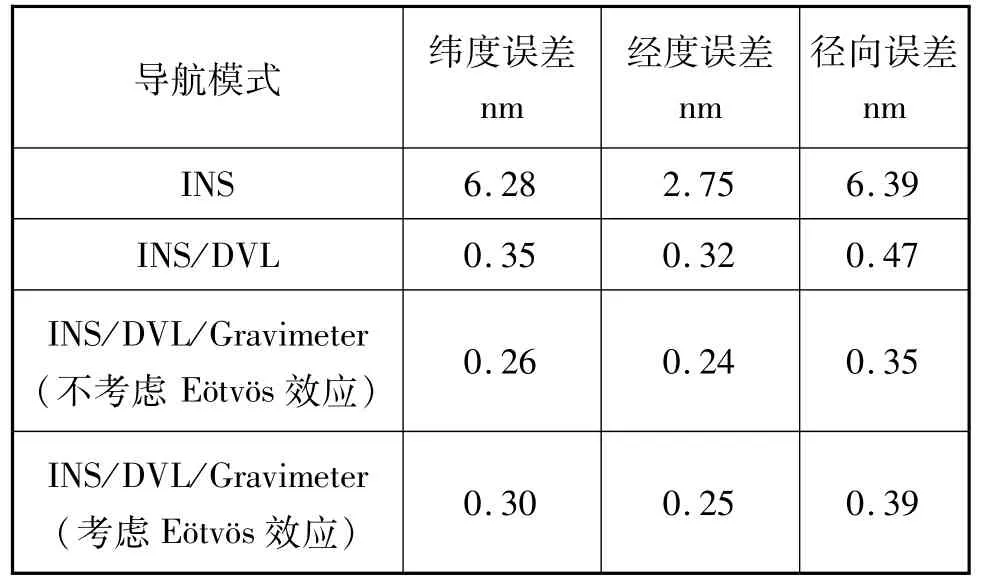
表3 不同导航模式最大误差统计Tab.3 Maximum error statistics of different navigation modes

利用卫星导航系统输出的速度和位置信息估计厄特沃思校正值，并作为参考基准。分别计算上述四种导航模式下的厄特沃思校正值，及其与参考基准之间的差异，如图11和图12所示，统计厄特沃思估计误差最小值、最大值、均值和标准差结果如表4所示。

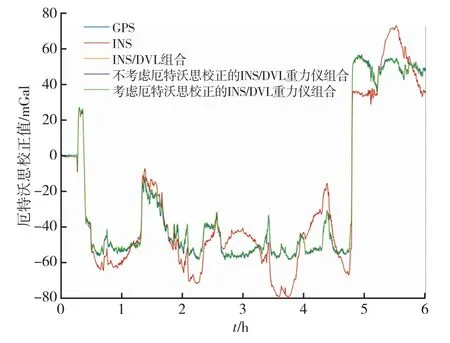
图11 不同导航模式计算的厄特沃思校正值Fig.11 Eötvös effect in different navigation modes

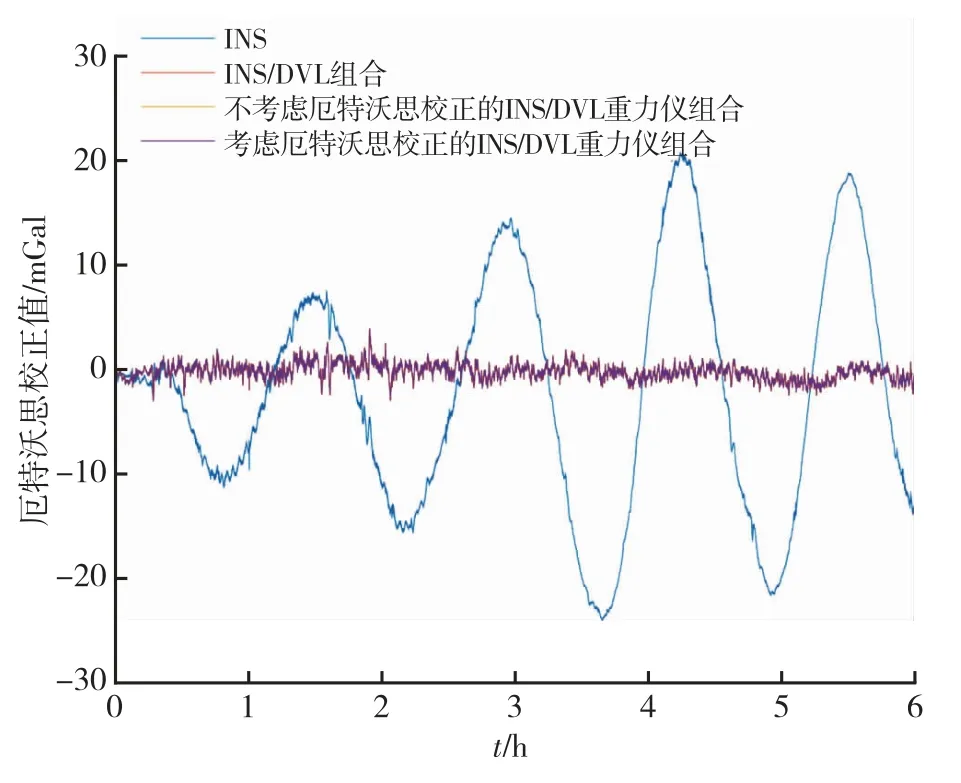
图12 不同导航模式计算的厄特沃思误差Fig.12 Eötvös errors in different navigation modes

根据表4可知，将纯惯性推算得到的导航信息作为厄特沃思校正计算参数时，厄特沃思估计误差最小值为－23.73 mGal，最大值为21.28 mGal，均值为－1.84 mGal，标准差为11.19 mGal。当引入DVL辅助信息源时，厄特沃思估计误差最小值为－2.63 mGal，最大值为4.33 mGal，均值为0.20 mGal，标准差为0.75 mGal，厄特沃思校正值得到了较好地估计。

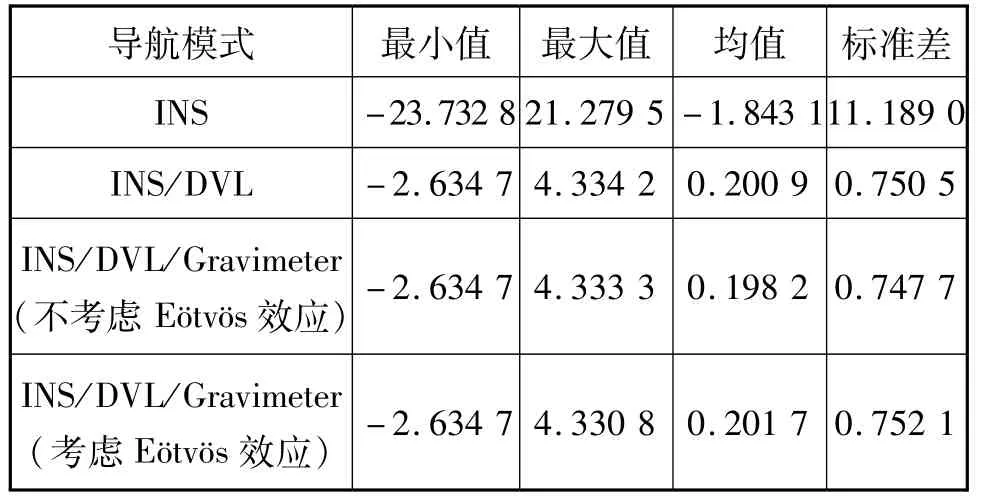
表4 不同导航模式计算的厄特沃思误差统计Tab.4 Eötvös error statistics of different navigation modes

5 结束语

针对水下卫星导航系统拒止环境，重力仪的厄特沃思校正难以精确估计问题，本文构建了水下INS／计程仪／重力仪组合导航框架，采用UKF非线性滤波算法，分析了不同导航模式下厄特沃思估计误差特性，对比分析了有无厄特沃思估计误差时重力辅助导航性能差异。半物理仿真试验表明，引入DVL测量信息时，厄特沃思估计误差均值为0.20 mGal，标准差为0.75 mGal，较好地估计了厄特沃思效应。同时对比仿真分析了四种不同导航模式的定位性能，结果表明采用DVL的辅助导航方式可有效抑制惯导误差积累，INS／DVL／Gravimeter三者信息融合模式定位性能进一步提高，即使在考虑厄特沃思估计误差的情况下，与仅采用DVL作为辅助信息源相比，水平径向误差定位精度依然提升了17.02%。