基于拉普拉斯矩阵的网络社区划分算法在电缆网测试中的应用

王 兵，魏志强，蔡文杰，闫佳晖，张莉莉，赵 凯

（1.北京航天计量测试技术研究所，北京 100076；2.中国运载技术火箭研究院，北京 100076）

1 引 言

在大型工程项目中使用大量电缆，这些电缆盘根错节构成了复杂的电缆网，各种控制和供电信号在其中穿梭，犹如人体中的神经系统，支撑着大型工程项目各种重要信息的交互。其中的低频电缆如同装备中的血液，为各种元器件传输能量。在大型工程项目使用前，为保证任务的成功率，必须要进行低频电缆网的导通绝缘性能测试。低频电缆网的测试从早期的绝缘电表和万用表测试，发展到今天的使用自动化仪器电缆网测试仪进行测试，测试效率成倍提升。电缆网测试仪通过转接电缆将被测电缆网的芯点统一到统一的接口连接器接入电缆网测试仪进行测试。其中转接电缆起到桥梁作用，将工装不一的被测电缆统一到相同的工装中。转接电缆的常规设计方法是针对每一个测试节点工装设计相应的转接电缆，然后根据测试网络芯点间连接关系，使用对应转接电缆进行测试，如图1所示。但是这种测试方案由于单次测试接入测试仪的统一接口数量有限，导致测试效率较低。所以需要设计新型的转接电缆和测试方案提高电缆网测试效率。

图1 常规转接电缆设计示意图Fig.1 Schematic diagram of conventional converter cable design

本文从实际需求出发，采用改进型转接电缆设计方法，如图2所示，通过将不同工装对应的转接电缆设计到同一根转接电缆中，充分利用统一工装接口的芯点，以达到提高测试效率的目的。针对其中复杂电缆网子网络划分困难的问题，提出基于拉普拉斯矩阵的网络社区划分算法完成复杂关联性强的电缆网子网络划分，从而确定转接电缆和测试方案的设计，开展了网络社区划分算法在电缆网测试中的应用研究，从方案原理和仿真对比两方面进行了验证。

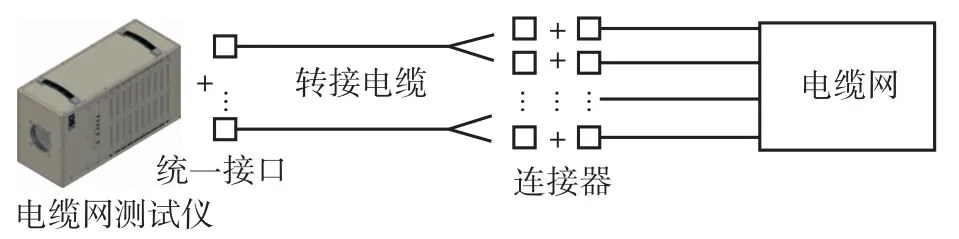
图2 改进的转接电缆设计示意图Fig.2 Schematic diagram of improved conversion cable design

2 算法原理及应用分析

2.1 算法原理

对电缆网进行导通绝缘测试时，需要设计转接电缆，将电缆接口统一为相同的连接器。将整个电缆网划分为小于电缆网测试仪最大接入芯点数的子网络，并设计转接电缆和测试方案进行测试。

在电缆网测试中，在忽略电缆网各接口节点芯点数量的前提下，可将被测电缆网抽象为具有n个节点，且节点间存在连接关系的无向节点网络G，如图3所示。测试电缆网绝缘导通关系即可抽象为测试无向节点网络G中n个节点的连接关系。所以，转接电缆的设计问题转化为无向节点网络G的子网络划分问题，只要将完整的电缆网划分为关联性弱的一个个子网络，就可以根据子网络进行转接电缆的优化设计。

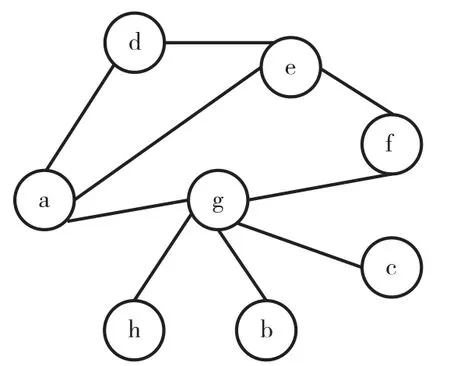
图3 无向节点网络GFig.3 Node network G

无向节点网络G的子网络划分可以基于图论中的子图分割问题。对于无向节点网络G，其节点间的连接关系A可表示为邻接矩阵A，节点A表示节点i和节点j间的连接关系，如果A＝1，则节点i和节点j存在连通关系。反之，则不存在。而节点网络G是无向网络，所以A＝0，且A＝A。

同时无向节点网络G某一节点i与其他节点连接关系的权值可构造为度矩阵D。

从而可以得到拉普拉斯矩阵L＝D－A。

拉普拉斯矩阵有一些特性：

（1）在存在的特征值λ中，如果在G中存在k个子网络，那么有k个λ＝0，这样就可以通过特征值判断网络G中存在多少子网络；

（2）最小特征值是0；

（3）最小非零特征值是图的代数连通度，即表征网络节点间的紧密程度，最小非零特征值越接近，网络节点越紧密，反之越稀疏。同时最小非零特征值对应的特征向量对应各个网络节点，特征向量的大小又反映了节点间的紧密程度。

所以可以借助拉普拉斯矩阵的以上特性作为网络划分的依据，得到最优网络节点划分。

2.2 应用分析

复杂电缆网导通绝缘测试网络具备无向多分量的特点，并且往往是一个复杂的整体网络，所以利用以上特性，可以利用无向网络G的拉普拉斯矩阵的最小非零特征值对应的特征向量得出哪些节点偏向组成一个子网络的结论。

以某电缆网为例，设计过程如下：

（1）将复杂电缆网输入文件抽象为无向网络G；

（2）计算无向网络的邻接矩阵A和度矩阵D；

（3）得到拉普拉斯矩阵L＝D－A；

（4）计算拉普拉斯矩阵的特征值及特征向量；

（5）统计特征值等于0的个数，若大于1，则根据特征值0对应的特征向量大小进行子网络划分，得到的子网络为完全独立的子网络。若第二小特征值大于0，则取第二小特征值对应的特征向量作为拉普拉斯矩阵L的变换依据，将L矩阵中元素依据特征向量升序或降序进行变换，可得最优子网络划分矩阵K，可根据图中的连接关系紧密程度逐个划分子网络以设计转接电缆。同时根据矩阵K中的节点顺序，得到电缆网测试顺序优化方案。

3 仿真验证

假设电缆网测试仪只有两个插槽，每个插槽32芯点，共64芯点。每个节点都具有不同的芯点以及芯点间连接关系，如图4所示。分别使用常规转接电缆设计方法和测试方案与改进后的设计方法和测试方案就测试效率做对比。

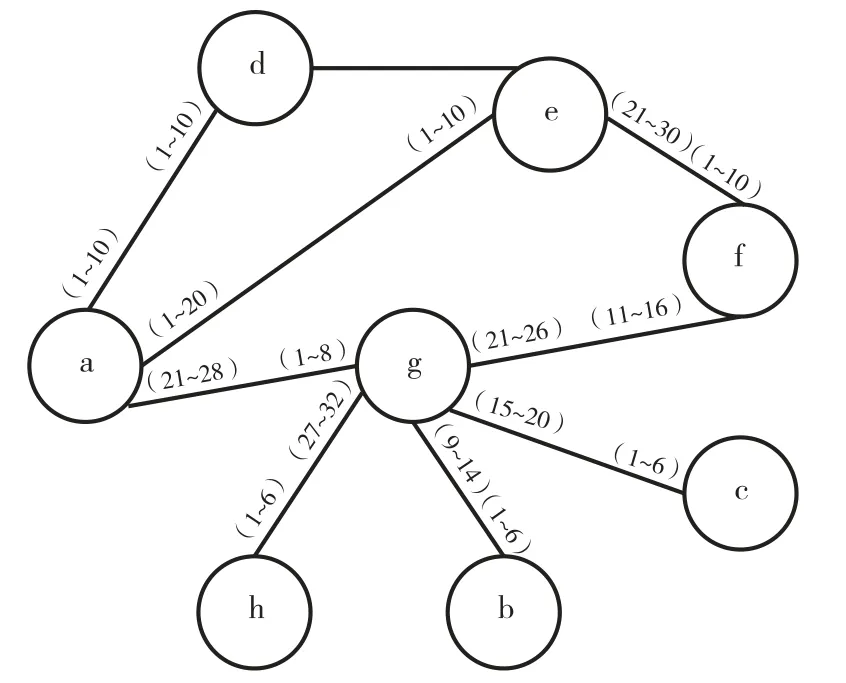
图4 电缆网络芯点连接关系图Fig.4 Cable network core point connection diagram

3.1 转接电缆常规设计法

转接电缆常规设计法是针对每一根被测电缆的连接器设计对应的专用转接电缆，基于此得到的转接电缆设计方案如表1所示。

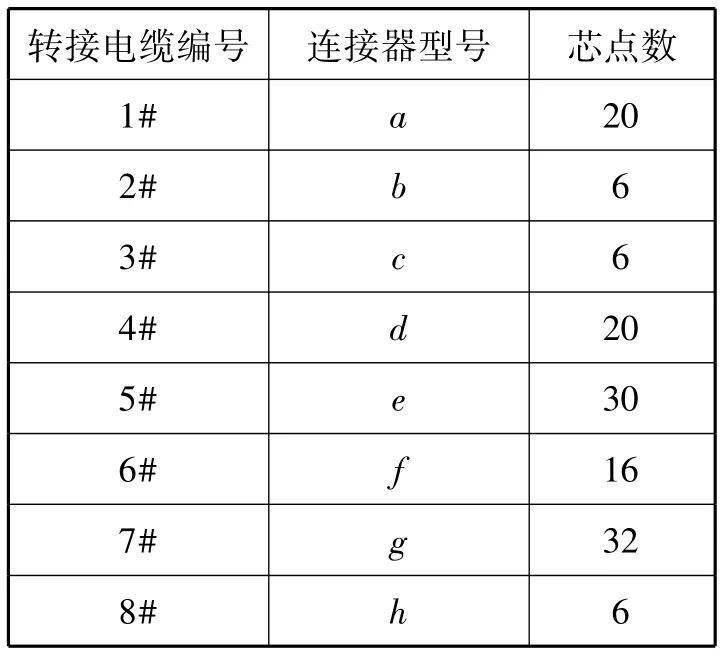
表1 常规设计方法设计的转接电缆设计方案Tab.1 Conventional design method to design the onversion cable design scheme

由转接电缆设计方案和电缆网测试仪的接口信息，以及测试均最大化使用测试仪背板插槽的原则，得到电缆网测试插拔顺序如表2所示。

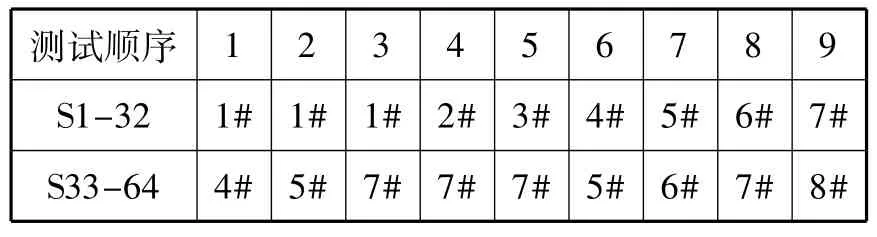
表2 常规设计方法电缆网测试插拔顺序Fig.2 Conventional design method cable network test plug and unplug sequence

需要制作1＃～8＃八根转接电缆。根据上表需要进行9次电缆网测试，进行9次插拔。

3.2 转接电缆改进设计方案

针对上述网络使用基于拉普拉斯矩阵的社区划分算法进行转接电缆和测试方案设计。根据第2章算法原理可得拉普拉斯矩阵，如图5所示。

图5 拉普拉斯矩阵表示的节点连接关系Fig.5 Node connection relationship represented by Laplace matrix

通过计算可得矩阵特征值分别为0，0.585 8，1，1，1.763 9，3.414 2，4，6.236 1。第二小特征值对应特征向量为0.298，－0.393 4，－0.393 4，0.488 9，0.393 4，0.163，－0.163，－0.393 4。将L矩阵中元素依据特征向量升序进行变换得到以下矩阵，如图6所示。

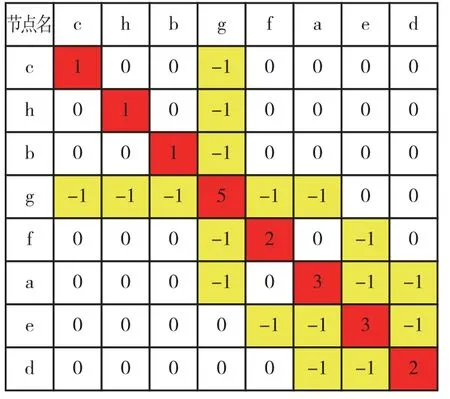
图6 经变换后的节点连接关系Fig.6 The node connection relationship after transformation

从而得到转接电缆设计方案见表3。表3中列出了优化后的转接电缆设计方案，根据节点划分将关联性较大的连接器集成在一个转接电缆上，扁插头芯点得到充分利用。

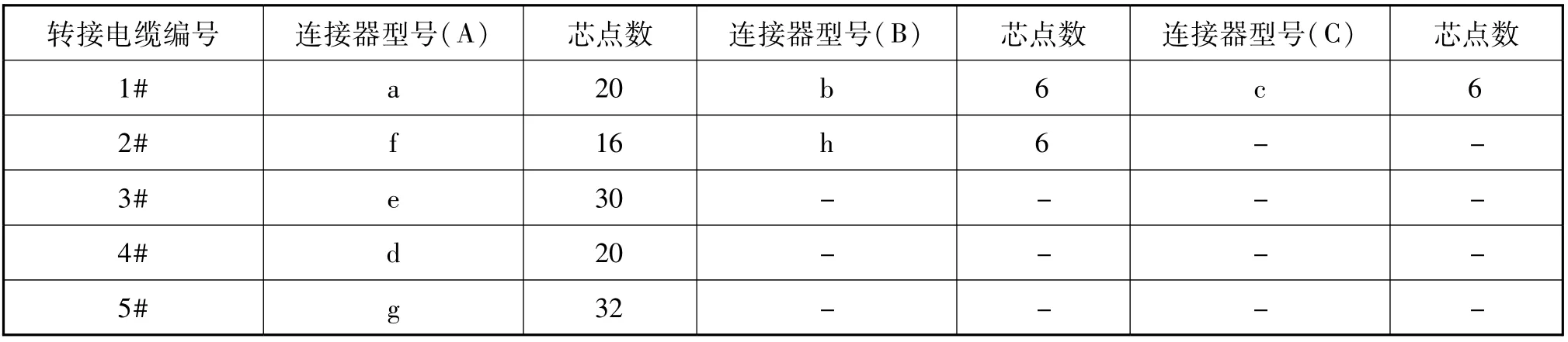
表3 改进的转接电缆设计方案Tab.3 Improved conversion cable design scheme

由于使用上述方案，扁插头芯点数得以合理分配和充分利用，得到电缆网测试插拔顺序，见表4。

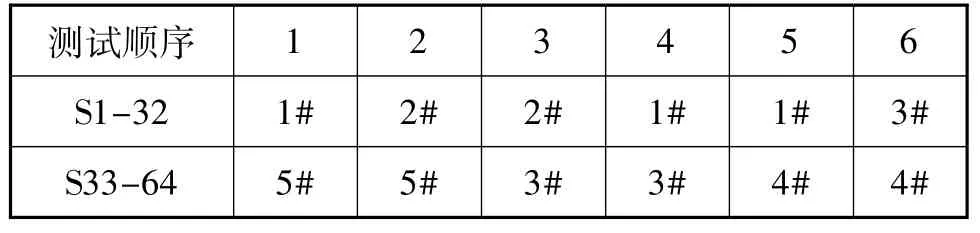
表4 改进的转接电缆测试插拔顺序Tab.4 Improved insertion and unplugging sequence of adapter cable test

共需6次测试，6次插拔，大大节省了电缆网测试仪转接电缆的插拔时间，测试效率大大提高。

综上所述，经过改进设计后的转接电缆设计方法较常规转接电缆设计方法，一方面减少了统一工装连接器数量，降低了物料成本；另一方面通过减少插拔次数，减少了测试所需时间，提高了电缆网测试效率。

4 结束语

针对复杂电缆网中常规设计法设计的转接电缆存在测试效率低的痛点问题，提出了基于拉普拉斯矩阵的社区网络划分算法进行转接电缆设计，实现了更高效率的电缆网测试。与常规转接电缆设计方法相比，提升了单次接入电缆网有效测试芯点的数量，以此提高芯点的测试效率。本文设计的转接电缆设计方案具有简单易行的特点，为有效解决电缆网测试仪单次接入有效芯点最大化提出了合理方案。