更上一层楼：从一题多解到揭示结构

刘东升

几何题的一题多解是不少同学的兴趣点。如果能从一题多解发展到揭示结构，则能让我们理解得更加深刻。下面，老师以一道几何题为例，跟同学们一起从一题多解走向揭示结构。

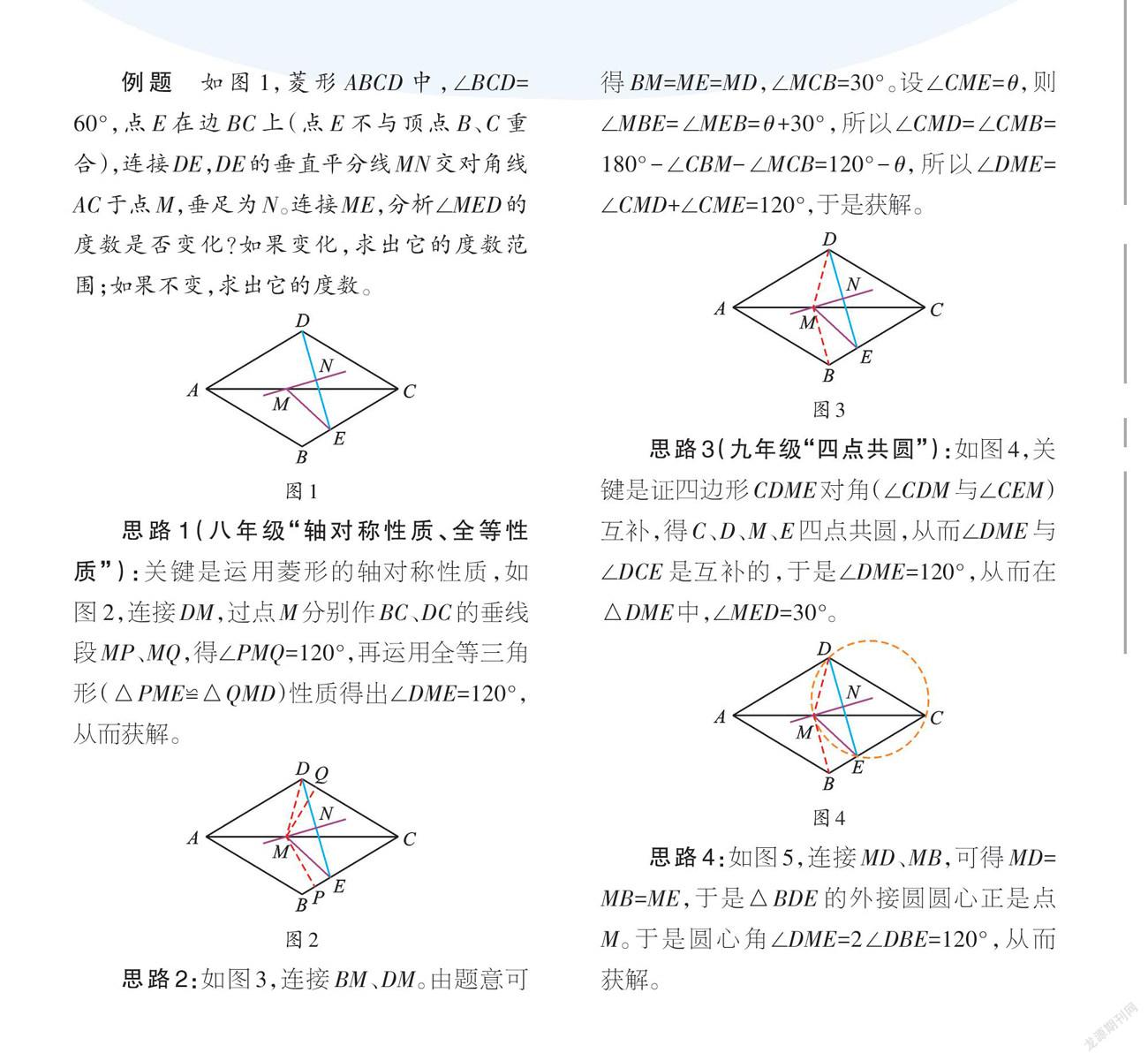
例题 如图1，菱形ABCD中，∠BCD=60°，点E在边BC上（点E不与顶点B、C重合），连接DE，DE的垂直平分线MN交对角线AC于点M，垂足为N。连接ME，分析∠MED的度数是否变化？如果变化，求出它的度数范围;如果不变，求出它的度数。

思路1（八年级“軸对称性质、全等性质”）：关键是运用菱形的轴对称性质，如图2，连接DM，过点M分别作BC、DC的垂线段MP、MQ，得∠PMQ=120°，再运用全等三角形（△PME≌△QMD）性质得出∠DME=120°，从而获解。

思路2：如图3，连接BM、DM。由题意可得BM=ME=MD，∠MCB=30°。设∠CME=θ，则∠MBE=∠MEB=θ+30°，所以∠CMD=∠CMB=180°-∠CBM-∠MCB=120°-θ，所以∠DME=∠CMD+∠CME=120°，于是获解。

思路3（九年级“四点共圆”）：如图4，关键是证四边形CDME对角（∠CDM与∠CEM）互补，得C、D、M、E四点共圆，从而∠DME与∠DCE是互补的，于是∠DME=120°，从而在△DME中，∠MED=30°。

思路4：如图5，连接MD、MB，可得MD=MB=ME，于是△BDE的外接圆圆心正是点M。于是圆心角∠DME=2∠DBE=120°，从而获解。

【继续探究】由于含60°的菱形可看成是两个等边三角形“拼接”在一起，于是我们将其中一个等边三角形删减，得出以下“等价问题”。

如图6，在等边三角形ABC中，点E是BC边上的动点，F为线段AE的中点，线段AE的垂直平分线交AB边的中线于点G，那么∠GEF是否为定值？如果是定值，请求出这个值;如果不是，请说明理由。

【思路解析】如图7，取BE的中点P，连接PF、PG、BG、AG，可得BG=AG=EG，于是GP⊥BE。在四边形EFGP中，根据对角互补，可得E、F、P、G四点共圆，所以∠FGE=∠FPE。再把目光切换至△EAB中，FP∥AB，所以∠FPE=∠ABC=60°，于是由“同弧所对圆周角相等”，可得∠FGE=∠FPE=60°，从而在Rt△EFG中，∠GEF=30°。

【揭示结构】如图8，作△CDE（∠DCE=α）的外接圆，交CG（∠ECD的角平分线）于点G，那么弧GD与弧GE相等，GD=GE。于是∠GEF=∠GCD=[12]∠DCE=[12]α。

可以发现，原题中的含有60°的菱形是更强的条件。60°可以换为任意角α，答案都是[12]α。

【问题推广】已知△ABC，点E是直线BC上动点，线段AE、AB的垂直平分线交于点G，求证：∠AEG=[90°-∠ABC]。

【简证】以图9为例，圆心角∠AGE=2∠ABC，从而∠FGE=∠ABC，于是∠AEG=90°-∠ABC。随着点E在直线BC上运动到不同位置，用类似的方法可以证明∠AEG=[90°-∠ABC]。

（作者单位：江苏省南通市教育科学研究院）12B9E5C7-7940-4B8A-9440-F9D9C259077D