巧妙设计认知冲突

王程程

[摘 要]数学教学活动通过矛盾冲突来唤起学生的求知需求，激发学生的学习兴趣，由此推进新知的探究进程。在教学中，教师可在旧知铺垫中用冲突有效对接，在情境中用冲突激发兴趣，在比较辨析中用冲突明确本质，以丰富学生的认知建构过程。文章以“中位数”的教学为例阐述概念性教学中巧妙设计认知冲突的重要性。

[关键词]认知冲突;平均数;中位数

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）08-0063-03

认知冲突指的是人们在认知发展过程中，当原有概念（或认知结构）与现实情境不相符时在心理上所产生的矛盾或对立。这种冲突会成为学生学习道路中的障碍，会给学生的新知学习带来困难。如果教师能巧妙设计和利用认知冲突，便能唤起学生的求知需求，激发学生的学习兴趣，由此推进新知的探究过程。

平均数、众数和中位数是小学数学的三个基本统计量，这三个统计量可让学生体会到数学在现实生活中的广泛应用，从而促进学生将数学充分应用在日常生活中。在统计学上，平均数、中位数、众数都是描述数据的集中趋势的特征数，但是它们反映的数据基本特征有所不同，它们从不同角度提供了同一组数据的真实面貌，因此它们有着不同的含义和适用范围。小学生的思维能力比较薄弱，要准确使用这三个统计量有一定的难度。本文主要阐述如何借助学生已有的“平均数”知识和熟悉的生活情境巧妙设计认知冲突，进而引导学生比较和辨析“中位数”，从而明确其本质。

一、利用旧知，引发冲突，促进探究

《义务教育数学课程标准（2011年版）》指出：“数学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。”建构主义也认为，学习并不是简单地将知识进行堆砌，而是新旧知识和已有经验的相互作用而发生的知识重组和知识网的重建。这些都告诉我们，在教学中要关注学生的学习起点。在学习中位数以前，学生就在三年级认识了平均数，初步了解了平均数的概念;四年级又进一步学习了平均数，掌握了平均数的含义及其求法。其中，教材中的“平均数”的课后练习“你知道吗？”引导性地提出：“在演唱比赛中，每个评委都要为选手打分。计算选手的得分时，往往要去掉一个最高分和一个最低分。这是因为每个评委的欣赏角度不同，每个人给同一位选手打出的分数也就不同。去掉一个最高分和一个最低分，可以剔除一些极端数据，使最后的得分更加公平合理，更能代表选手的实际水平。”这里渗透的解决现实问题的思想为学生日后学习中位数埋下了伏笔。

教师在教学中便可以利用平均数与中位数的特征差异，让学生产生认知冲突，从而激发学生的求知需求。

[教学片段一]

师：小芳第一次单元测试的成绩是85分。学期结束，以这个85分作为小芳的平时成绩，你认为合理吗？说说你的理由。

生1：不合理。一次成绩并不能充分体现小芳学习的真实水平。

生2：不合理。我觉得应该用多次单元测试的成绩的平均数来代表学期成绩。

【设计意图：从学生熟悉的单元测试成绩入手，调动学生参与的积极性，促使学生回顾已学过的“平均数”概念。】

师（小结）：是的，平均数能反映同学们学习的一般水平。（板书：平均数）

师：下面老师带来了一个实际问题。（展示问题及相关数据，如表1）如果你是应聘者，你会选择哪家公司？

生3：会优先考虑工资待遇高的公司。

师（追问）：那哪个数据能表示甲公司员工工资的一般水平呢？乙公司呢？

【设计意图：由工资话题入手，激发学生的学习兴趣。】

师：请你算一算。可以使用计算器计算。

（學生独立完成，教师巡视，收集学生答题过程并展示。）

展示学生作品：

甲公司：（2900+3100+2600+3000+3200+2800+3400）÷7=3000（元）

乙公司：

方法1：（2200+1800+1900+2400+1700+2000+9000）÷7=3000（元）

方法2：（2200+1800+1900+2400+1700+2000）÷6=2000（元）

方法3：（2200+1800+1900+2400+2000）÷ 5=2060（元）

师：对于甲公司，这里求的是什么？它能不能反映甲公司员工的一般工资水平？

生4：由于甲公司6位员工和经理的工资水平相差不多，因此我们可以用7个人的平均工资来反映甲公司员工的一般工资水平。

师：那乙公司呢？我发现有3种解法。为什么要这样做？

生5：方法1跟处理甲公司的方法一样，用7个人的平均工资来反映乙公司员工的一般工资水平。

生6：方法1求得平均数3000元，乙公司只有1人的工资超过了3000元，其余6人的工资都低于3000元。因此，平均数3000元不能反映乙公司员工的一般工资水平。

生7：方法2关注到经理的工资9000元远远高于其他员工的工资，因此计算时去掉了最高工资9000元，求的是剩下6位员工的平均工资，以此来反映乙公司员工的一般工资水平。

生8：方法3同时剔除了乙公司7个人中的最高工资和最低工资，求出了剩下5位员工的平均工资，以此来反映乙公司员工的一般工资水平。

师：生活中有没有这样的例子？是怎么处理的？

生9：生活中我们在算比赛成绩时也会去掉最高分和最低分，求出剩下分数的平均分，以此来代表参赛选手的最终得分。

师（小结）：通常，我们可以用平均数来反映一组数据的一般水平，但当这组数据中有极端数据出现时，用平均数来反映就不合适了。

二、借用情境，诱发冲突，激发兴趣

利用工资水平的问题情境，让学生初步感受到并不是所有数据都适合用平均数来表示它们的平均水平，从而引发学生的认知冲突，激发学生继续探究的欲望。随后，在特殊情况的教学中，新概念“中位数”便应运而生。

[教学片段二]

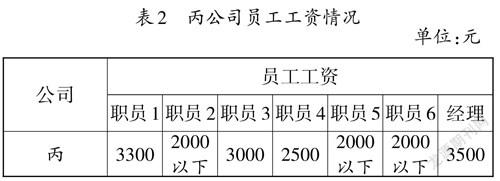
师：刚刚乙公司的数据很特殊，有一个极端数据。像这样的特殊情况还有很多，让我们再来看看丙公司的数据。

出示表2：

师：你认为丙公司的这组数据特殊在哪？

生1：丙公司里有几位员工的具体工资不知道，也就是数据不全。

师：那你打算用什么数来反映这组数据的一般水平呢？

（学生独立思考后小组交流，教师呈现学生的想法。）

师：“去数”是什么意思？这种方法有道理吗？

生2：“去数”是指去掉极端数据，即在表示这组数据的平均水平时把极端数据去掉。

师：这样做看上去有点乱，你有什么更好的建议吗？

生3：可以先排序再“去数”。

师：用最中间的这个数表示丙公司员工的一般工资水平，行不行？

生4：还是有一定的道理的。

师：是平均数吗？

生5：不是。

师：我们叫它中位数。

【设计意图：借助丙公司员工数据不全的情境，进一步引发学生的认知冲突，激发学生解决问题的欲望，同时引出本节课的学习内容——中位数。】

师：中位数也是反映一组数据一般水平的常用统计量。

师：我们再来看看乙公司，用平均数3000元不能反映乙公司员工的一般工资水平，那用中位数行吗？

（学生独立思考）

师：中位数是多少？你有什么发现？

生6：通过排序去数，我得到乙公司员工工资的中位数是2000元，与去掉最小数据和最大数据之后的那组新数据的平均数比较接近。

师：那可以用中位数来反映乙公司员工的一般工资水平吗？

生7：可以。

师：由此，我们可以看出，当一组数据中有极端数据时，平均数不能客观反映这组数据的一般水平，这时可以用中位数来反映这组数的一般水平。

三、比较辨析，开掘冲突，认清本质

教育家乌申斯基指出：“比较是一切理解和思维的基础。”在学习新知时适当运用比较策略，通过鲜明的对比，让学生产生认知冲突，可以提高学生对知识的运用能力和辨识能力，从而更好地把握知识的本质。

学生刚刚学习了中位数，对其有了初步的认识。为了加强学生对中位数概念的理解，同时让学生知道在不同的情况下如何正确使用中位数与平均数，可引导学生进行比较和辨析，由此进一步引发学生的认知冲突，促进学生认识平均数和中位数的本质。

[教学片段三]

出示相關数据：

下面是某校3班两组同学家庭住房的面积（单位：平方米）。

①96、92、90、94、89、91、93、97、95;

②86、84、88、275、82、80、83、81、87。

师：观察和分析数据的特点，求出两组数据的平均数和中位数。再想一想，用怎样的数据来反映每组学生家庭住房面积的一般水平比较好？

生1：数据①的平均数和中位数都是93;数据②的平均数是105，中位数是84，两者相差比较大。

生2：数据①可以用平均数来反映数据的一般水平;数据②中有个极高数据，大大提高了这组数据的平均数，这时再用平均数来反映数据的一般水平就不合适了。

师：组内数据比较接近，可以用平均数来反映这组数的一般水平。极端数据不仅有极低数据，还有极高数据，有极端数据时用中位数来反映一组数据的一般水平比较合适。平均数比中位数更为精确，它受到数据中每个数据的影响，而中位数比较“粗糙”。

[教学片段四]

出示：

有两组男生比赛套圈，每组5人，每人有圈20个。以下是两组男生的得分情况。

第一组：15、18、19、19、17。

第二组：18、19、20、7、4。

师：求出两组数据的中位数。用什么数来反映这两组男生的套圈水平比较合适？

生1：第一组数据的中位数是18，第二组数据的中位数也是18。

生2：两组数据的中位数相同，无法用中位数来比出两组男生的套圈水平。

师：是的，这里组内的5位男生都是参赛选手，每个人的成绩都要算进去，就像我们平时用班级的平均分来反映班级的一般水平一样。因此，这里并不能用中位数来反映两组男生的套圈水平。那你觉得用什么比较合适？

生3：平均数！

师：在选择统计量来反映一组数据的一般水平时，不仅需要考虑数据的特点，还要考虑实际生活的需要。

综上，通过巧妙地设计认知冲突，使学生在旧知中发现了区别，在探索中发现了新知，在对比中认清了本质。通过本课的设计，我们清楚地看到，对于小学阶段所要接触的三个统计量——平均数、中位数、众数，教师都可以利用这样的方法来进行教学。同时，所选的教学案例应尽量选用学生熟悉并感兴趣的内容。这样做便于学生发现数学在生活中的用处，激发学生的参与意识和学习兴趣，也让学生在冲突中探究新知，发展学生的数学思维，最后在冲突中通过比较，更加充分地了解同类概念的联系和区别。

[ 参 考 文 献 ]

[1] 朱德全.数学新课程标准与主题式教学设计[J].课程·教材·教法，2002（12）：33-35.

[2] 张向林.《中位数》教学分析[J].小学教学研究，2012（26）：5-6.

[3] 盛大启.苏教版小学数学教师用书：六年级下册[M].南京：江苏教育出版社，2013：12.

[4] 陈贻胜.断砖可为玉 点石能成金：例谈数学教学中形成认知冲突的策略[J].教育实践与研究（A），2011（6）：46-48.

（责编 黄春香）