具有健康教育的戒烟模型的稳定性分析
2022-05-31唐永鲁顾银鲁宋桢桢
唐永鲁,顾银鲁,宋桢桢
(银川能源学院 基础部,宁夏 银川 750105)
吸烟在明世宗嘉靖年间就已经开始,至今仍然有很大比例的成年公民和青少年在吸烟.2000年Castillo-Garsow等[1]第一次提出一个简单的戒烟模型,他们考虑了一个系统,将人群分为三个仓室:潜在吸烟者、吸烟者和戒烟者.文献[2-4]研究了具有健康教育的吸烟动力学模型.
文献[4]在Castillo-Garsow等[1]基础上,考虑了健康教育的因素,并建立了如下微分系统
(1)
其中,P表示未受教育的潜在吸烟者,E表示受教育的潜在吸烟者,S表示吸烟者,Q表示永久戒烟者.
吸烟能引起吸烟者患脑部疾病、呼吸系统疾病、血管类疾病等,二手烟还会对非吸烟者产生严重的影响.近些年来,国家出台各类政策:不允许在公共场合吸烟、吸烟有害健康宣传等.受到这些因素的影响,有些吸烟者就会选择临时戒烟或者永久戒烟.文献[5-7]主要针对含有临时戒烟模型做了稳定性分析.文献[8]考虑了“媒体和政府对吸烟的不连续干预策略”.文献[9]考虑了“人类行为”因素,建立模型并讨论了模型的稳定性.
文献[5]建立如下模型
(2)
其中,P表示未受教育的潜在吸烟者,L表示偶尔吸烟者,S表示吸烟者,R表示暂时戒烟者,Q表示永久戒烟者.
1 模型建立
在已有文献的基础上,将所研究的人群分为5个仓室:未受教育的潜在吸烟者P、受教育的潜在吸烟者E、吸烟者S、临时戒烟者R和永久戒烟者Q,并建立如图1所示的仓室图
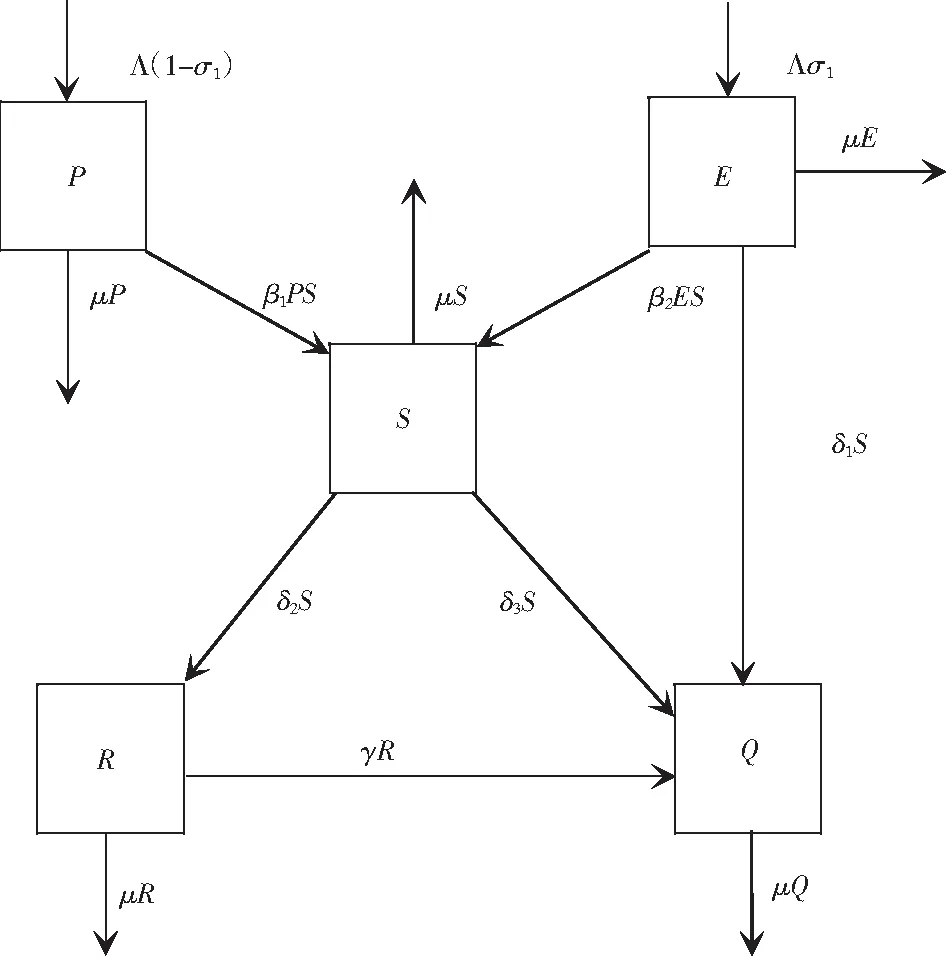
图1 模型的仓室图
对应于仓室图的常微分方程如下
(3)
其中,Λ表示总人数,σ1表示潜在吸烟者的受教育率,β1表示P与S的有效接触率,β2表示E与S的有效接触率,δ1表示E的有效戒烟率,δ2表示S的有效临时戒烟率,δ3表示E的有效永久戒烟率,γ表示R转化到Q的有效转化率,μ表示自然死亡率.
2 正性和有界性
定理1若P(0)>0,E(0)>0,S(0)>0,R(0)>0,Q(0)>0,则系统(3)的解P(t),E(t),S(t),R(t),Q(t)对于所有t>0都是正的.
证明假设结论不成立,则至少有一个不是正的.因此,有以下五种情况
(i)存在t1,使得:
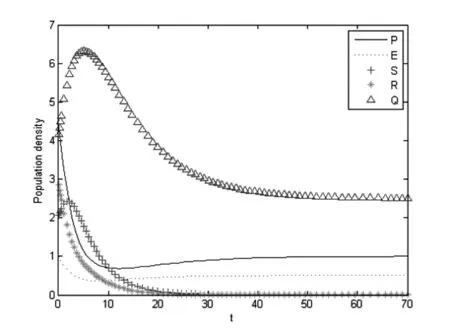
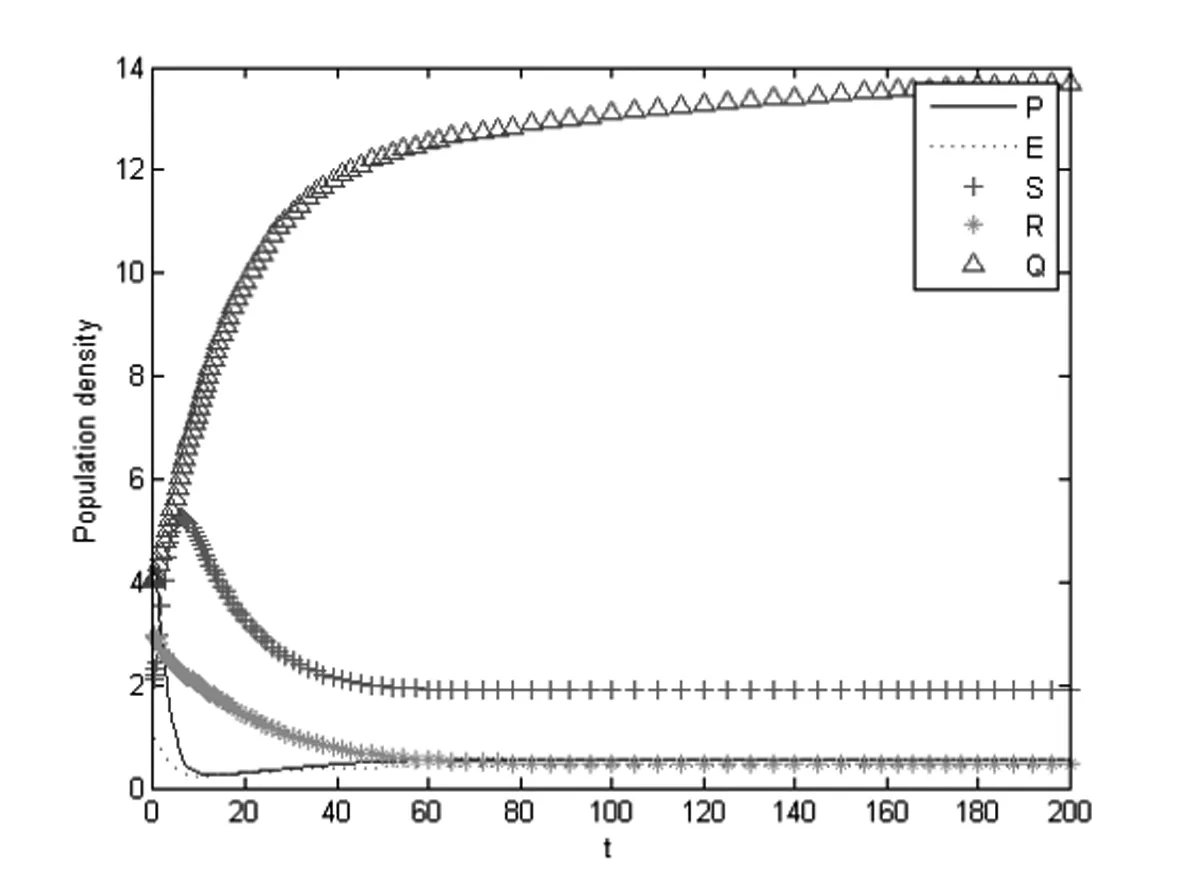
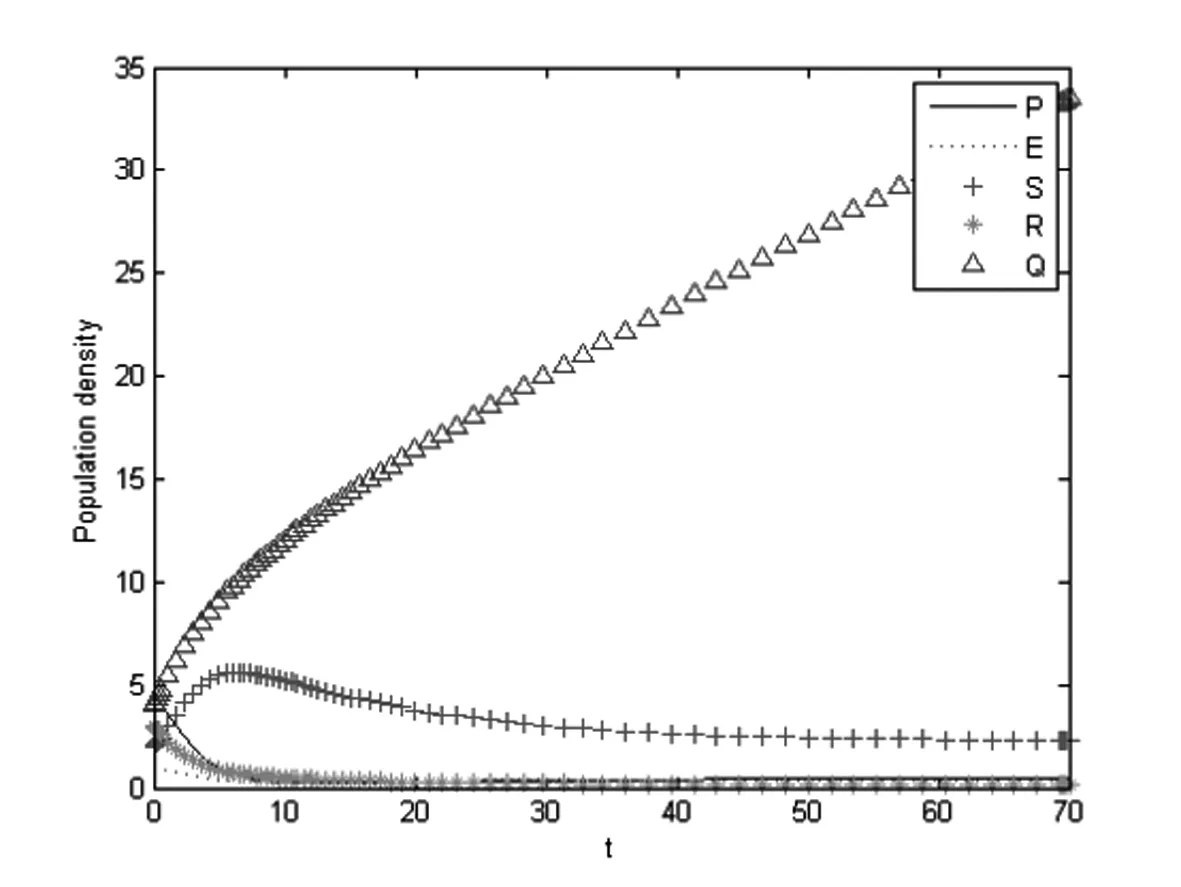
P(t1)=0,P′(t1)<0,E(t)≥0,S(t)≥0,R(t)≥0,Q(t)≥0,0 (ii)存在t2,使得: E(t2)=0,E′(t2)<0,P(t)≥0,S(t)≥0,R(t)≥0,Q(t)≥0,0 (iii)存在t3,使得: S(t3)=0,S′(t3)<0,P(t)≥0,E(t)≥0,R(t)≥0,Q(t)≥0,0 (iv)存在t4,使得: R(t4)=0,R′(t4)<0,P(t)≥0,E(t)≥0,S(t)≥0,Q(t)≥0,0 (vi)存在t5,使得: Q(t5)=0,Q(t5)<0,P(t)≥0,E(t)≥0,S(t)≥0,R(t)≥0,0 由(i)可知:P′(t1)=Λ(1-σ1)>0,与P′(t1)<0矛盾. 由(ii)可知:E′(t2)=Λσ1>0,与E′(t2)<0矛盾. 由(iii)可知:S′(t3)=0,与S′(t3)<0矛盾. 由(iv)可知:R′(t4)=δ2S(t4)>0,与R′(t4)<0矛盾. 由(vi)可知:Q′(t5)=δ1E+δ3S+γR>0,与Q′(t5)<0矛盾. 综上可得结论成立. 定理2系统(3)的所有可行解是有界的,并且可行域为 在无烟平衡点E0处的雅可比矩阵为 其中 证明由系统(3)可得 β1P*+β2E*-(δ2+δ3+μ)=0. (9) 将P*和E*代入(9)可得 a(S*)2+bS*+c=0, (10) 其中a=β1β2(δ2+δ3+μ),b=μβ2(δ2+δ3+μ)+β1(δ1+μ)(δ2+δ3+μ)-β1β2Λ,c=μ(δ1+μ)(δ2+δ3+μ)-β1Λ(1-σ1)(δ1+μ)-μβ2σ1Λ. 显然 a=β1β2(δ2+δ3+μ)>0, 因为 所以 μ(δ1+μ)(δ2+δ3+μ)-β1Λ(δ1+μ)<0. 再由 β2μ>β1(δ1+μ), 可得 c=μ(δ1+μ)(δ2+δ3+μ)-β1Λ(1-σ1)(δ1+μ)-μβ2σ1Λ<0, 所以,(10)式有唯一的正解. 定理4当R0≤1时,无烟平衡点E0是全局渐近稳定的. 证明构造Lyapunov函数 则 Λσ1-β2ES-(δ1+μ)E+β1PS+β2ES-(δ2+δ3+μ)S+ δ2S-(γ+μ)R+δ3S+δ1E+γR-μQ 因为E0为无烟平衡点,所以σ1=0,即 因为R0≤1,即β1Λ≤μ(δ2+δ3+μ)<μ2,所以 β1Λ-μ2<0. 综上,V′≤0成立. 由LaSalle不变集原理[11-12]知,当R0≤1时,无烟平衡点E0是全局渐近稳定的. 则吸烟平衡点E*=(P*,E*,S*,R*,Q*)是全局渐近稳定性的. 证明构造Lyapunov函数 则V*的导数为 (11) 将E*=(P*,E*,S*,R*,Q*)代入系统(3)可得 (12) 把(12)式代入(11)式得 考虑下面的变量替换 (1-v)[zδ3S*+yδ1E*+uγR*-v(δ3S*+δ1E*+γR*)] 显然 当x,y,z,u,v满足下列四个关系之一 u<1,v<1,z≥u≥v,y≥v, u>1,v>1,z≤u≤v,y≤v, u>1,v<1,u≥z≥v,y≥v, u<1,v>1,u≤z≤v,y≤v, 时,有V*≤0成立. 由LaSalle不变集原理[11-12],E*是全局渐近稳定性的. 给出系统(3)的数值模拟来验证上面的理论证明. 例1令λ=0.2,σ1=0.5,β1=0.1,β2=0.07,δ1=0.5,δ2=0.09,δ3=0.3,γ=0.3,μ=0.1.经过计算参数满足定理4,给出初值(4.5,1,2,3,4),则E0的全局稳定性如图2所示. 图2 当R0≤1时,无烟平衡点E0全局渐近稳定性. 例2令λ=0.2,σ1=0.5,β1=0.09,β2=0.07,δ1=0.03,δ2=0.02,δ3=0.05,γ=0.07,μ=0.01.经过计算参数满足定理5,给出初值(4.5,1,2,3,4),则E*的全局稳定性如图3所示. 图3 当R0>1时,吸烟平衡点E*是全局渐近稳定性. 例3令λ=0.2,σ1=0.8,β1=0.1,β2=0.07,δ1=0.5,δ2=0.4,δ3=0.3,γ=0.3,μ=0.1.经过计算参数满足定理4,给出初值(4.5,1,2,3,4),则E0的全局稳定性如图4所示. 图4 当σ1=0.8,δ2=0.4时,无烟平衡点E0全局渐近稳定性. 本文考虑了具有健康教育的戒烟模型,由定理4和定理5可知,基本再生数R0=1是病毒感染发生与否的阈值. 由图2和图4可以看出当σ1和δ2的取值变大时,吸烟者明显消失得更快,图4中的P,E,S,R,Q比图2更早的趋近于稳定状态.这说明如果提高戒烟教育成功率和出台一些戒烟的措施,会有更多的人进入戒烟的仓室,能够使吸烟者更快的消失. 和文献[4]比较,本文把戒烟分为暂时戒烟和永久戒烟,这样更加接近现实生活情况.文献[4]中只讨论了吸烟平衡点的局部渐近稳定性,而本文给出了吸烟平衡点的全局渐近稳定性.由于现在全国加强“吸烟有害健康”的教育宣传,相对文献[5]考虑“吸烟有害健康的健康教育”因素,使得模型更加复杂,也加大了模型讨论的难度. 由以上结论可以给出以下建议:可以加强“吸烟有害健康”的教育宣传,从而提高戒烟教育的成功率;也可以出台一些政策,比如公共场合禁止吸烟,通过强迫人民去戒烟,达到提高戒烟率的目的.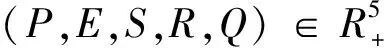
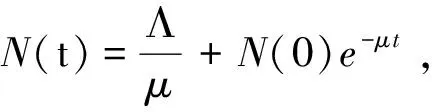
3 平衡点的存在性和基本再生数
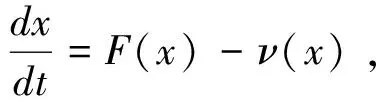


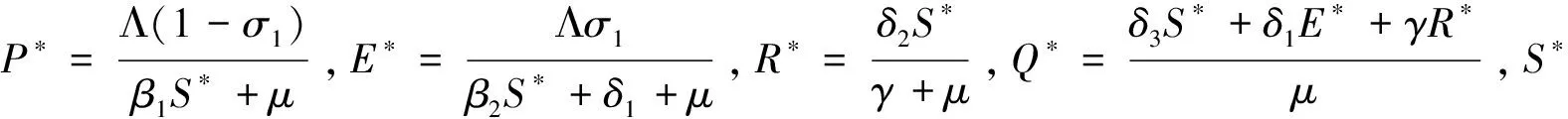
4 平衡点的稳定性分析
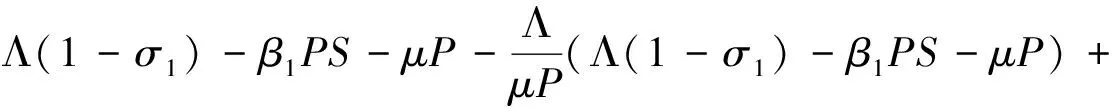
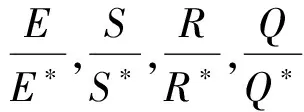




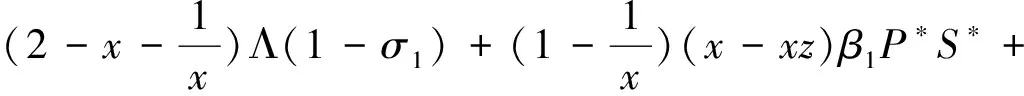


5 数值模拟
6 结论
