基于数学形态学的滑坡变形自动化监测方法设计

段志霞，赵 娜，宋 洁

(1.济源职业技术学院 基础部，河南 济源 459000；2.华东理工大学 数学学院，上海 200237)

斜坡上的土体或者岩体因受到雨水冲刷、地震及人工切坡等因素的影响，在重力作用下，沿着一定的软弱面或者软弱带顺坡向下滑动的自然现象被称为滑坡.据统计，滑坡造成的危害和影响仅次于地震灾害[1].

由于地理位置和气候等原因，我国的部分地区经常会产生滑坡、斜坡变形以及崩塌现象.据不完全统计，滑坡灾害已经威胁和危害到中国大约七十座城市的四百多个县，造成了巨大的损失[2].对滑坡变形展开监测是降低滑坡灾害造成的损失、防止灾害范围扩大的重要手段之一[3].

目前，提高对滑坡变形的监测效果已成为相关领域的重要研究课题之一.为了有效提高滑坡变形监测质量，本研究提出了基于数学形态学的滑坡变形自动化监测方法.

1 基于数学形态学监测滑坡变形

1.1 滑坡特征分析

在有坡度的坡上发生滑坡应具备两个条件.通常情况下，上下陡中缓坡度在10度和45度之间均为容易发生滑坡的地带，容易发生滑坡的地貌有建筑边坡、山坡以及开阔的铁路等.

滑坡体的形态特征与其类型和规模相关.发育完整的滑坡由下述几部分构成：滑坡体、滑动面、滑动带、滑坡床、滑坡壁、滑坡台阶、滑坡舌、滑坡周界、封闭洼地、主滑线以及滑坡裂缝.

1.2 基于数学形态学的滑坡变形图像采集与形态变换

在形变信号分析的过程中，主要利用卷积操作作为线性变换方式.这是因为不同频率谐波经过叠加能够形成音频或视频信号，而这样形成的信号无法用线性分解来展开具体分析，但能够根据偏序引入来构建数学模型.在对滑坡变形监测时，构建集合理论的滑坡变形图像算子较合理.因此，本文在利用测量机器人采集滑坡变形图像的基础上，利用数学形态学对滑坡变形图像实施形态变换.

数学形态学的基本运算主要包括腐蚀和膨胀、开运算和闭运算等[4].本文利用数学形态学的运算过程对滑坡变形图像做处理.过程如下

在E空间代数结构中添加与集合X∈E相关的平移量，可得到下式所示的结果

Xb={x+b∶x∈X}.

(1)

滑坡变形图像X中包括形状简单的集合B，利用下式表示集合B对图像X的腐蚀以及膨胀运算结果

(2)

其中，集合B表示结构元素.在此基础上进行复合运算后，可以得到

X∘B=(X⊗B)⊕B,X·B=(X⊕B)⊗B，

(3)

公式(3)分别代表集合B对X的开以及闭运算，然后采用本影的方式在图像形态变换的基础上获得滑坡变形图像的形态变换结果.

假设在膨胀运算后，Ta(f)能够生成集合簇Ta(f)⊕B，然后将该集合簇作为结构元素B对f(x)的膨胀

(f⊕B)(x)=sup{a∶x∈Ta(f)⊕B}.

(4)

其等价表达式为

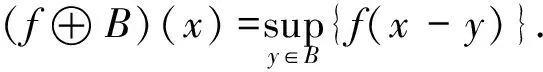
(5)

将Ta(f)⊗B作为阀集合函数，利用结构元素B对滑坡变形图像f(x)腐蚀

(f⊗B)(x)=sup{a∶x∈Ta(f)⊗B}，

(6)

其等价表达式为

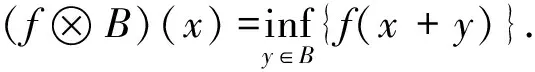
(7)

通过对(f⊕B)(x)和(f⊗B)(x)的分析，分别能够当作滑坡变形图像f(x)在点x的B窗口中局部最大和最小值，B还能够当作控制器，来控制滑坡变形图像的腐蚀或者膨胀范围[5]，以公式(4)和公式(6)为基础，引入B对滑坡变形图像实施开、闭运算，得到如下结果

f∘B=(f⊗B)⊕B,f·B=(f⊕B)⊗B.

(8)

采用滑坡变形图像g(x)当作结构元的形态运算，能够利用本影方法对其进行表示

(f⊕B)(x)=sup{a∶(x,a)∈U(f)⊕U(g)}，

(9)

(f⊗B)(x)=sup{a∶(x,a)∈U(f)⊗U(g)}.

(10)

公式(9)和公式(10)的等价形式如下

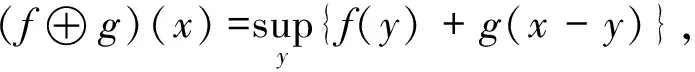
(11)

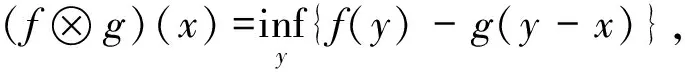
(12)

当g(x)=0,x∈spt(g)属于平坦结构元时，有

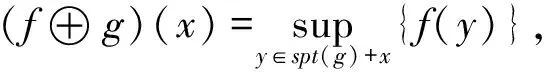
(13)

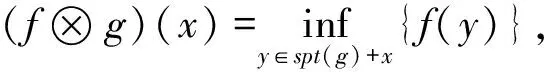
(14)

引入滑坡图像的形态开运算和闭运算

f∘g=(f⊗g)⊕g,f·g=(f⊕g)⊗g.

(15)

经过上述计算，完成对滑坡图像的形态变换处理，能够为滑坡变形监测的下一步研究奠定基础.

1.3 滑坡变形监测

监测滑坡变形图像数据的过程需要满足：在数据序列中，应保证零点数和极点数的数量相同，二者间的最大差值不应超过1[6-7].同时，时间应呈现局部对称关系；从原始观测的滑坡变形图像数据中选出本征模函数，步骤如下

步骤1 根据观测到的滑坡变形图像信号求出极值点x′(t)；

步骤2 采用样条函数按照极大和极小值点求取包络线emax(t)和emin(t)；

步骤3 计算包络线emax(t)和emin(t)二者间的平均值，并获得观测量与平均值之间的差值，认为是从滑坡变形图像观测信号中去掉的低频信号；

步骤4 计算剔除掉低频信号的极值点并不断迭代，一直到图像观测信号的包络线的平均值等于0；

步骤5 计算残差，并且只剩一个单调函数.

利用原有的观测数据构建滑坡变形监测模型，进一步分析滑坡体是否安全.通常情况下，在建立滑坡变形监测模型的过程中，应收集海量的观测数据，且要保证所采集的数据能够满足分布条件[8-9].而在实际监测过程中，有误差的滑坡监测数据中包含已知和未知的信息.因此，本文将监测模型视为灰色问题，灰色预测模型可以利用微分方程来描述，一元一阶模型为GM(1,1)，采用累加生成法来生成n期观测数据构成的时间序列，表达式如下

(16)

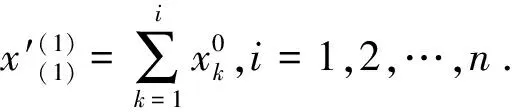
(17)

在此基础上，利用最小二乘准则计算灰参数[10]，过程如下

[αu]T=(B′TB′)-B′TL.

(18)

将公式(18)代入到微分方程中，可以求得解

(19)

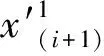
(20)

利用公式(20)实现了对滑坡变形的监测.

2 测试结果与分析

为了验证上述设计的基于数学形态学的滑坡变形自动化监测方法的可行性，设计如下验证过程.

实验以某滑坡为例，该滑坡在丘陵山区中，地质结构较为复杂，在开挖时受到机械作业振动和爆破的影响，在开挖工程周围建立排土场，排土场堆积越大滑坡体受力越大，稳定性变差，雨天会降低边坡岩土的受力情况，最终导致滑坡灾害.

在监测滑坡变形前，需要设计方案.本文实验中，采用电磁波测距三角高程法，通过设置待监测点和基准点共同对监测网的布设，基准点应该设定在离滑坡体远的稳定点处.以待监测点为目标点，认为滑坡体上目标点的运动情况能够反映滑坡变形的过程，通过监测点的数目、布设位置、滑坡的变形时间和滑坡体的规模能够确定滑坡变形的监测频率，以监测点滑坡前15期的变形监测数据为例，各期观测值的高程值如表1所示.

滑坡变形监测点的高程随时间的变化而下降，其中没有规律的随机因素也对其有影响作用，是由测量误差引起的.对滑坡变形的监测耗时展开测试，测试结果如图1所示.

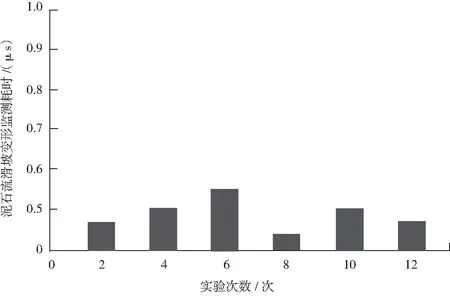
图1 滑坡变形监测耗时测试结果

分析图1可知，在对滑坡变形监测12次实验监测整体耗时均在0.6 μs以下，其中，第8次实验滑坡变形监测耗时最短，第10次实验滑坡变形监测耗时为0.5 μs.滑坡变形监测耗时越短说明监测的实时性较好.

在对滑坡变形监测耗时测试的基础上，进一步测试滑坡变形监测的正确率.正确率的计算过程如下

(21)

式中，σ代表滑坡变形监测正确率，TP代表得到正确监测结果的次数，TN代表监测总次数.具体的测试结果如图2所示.

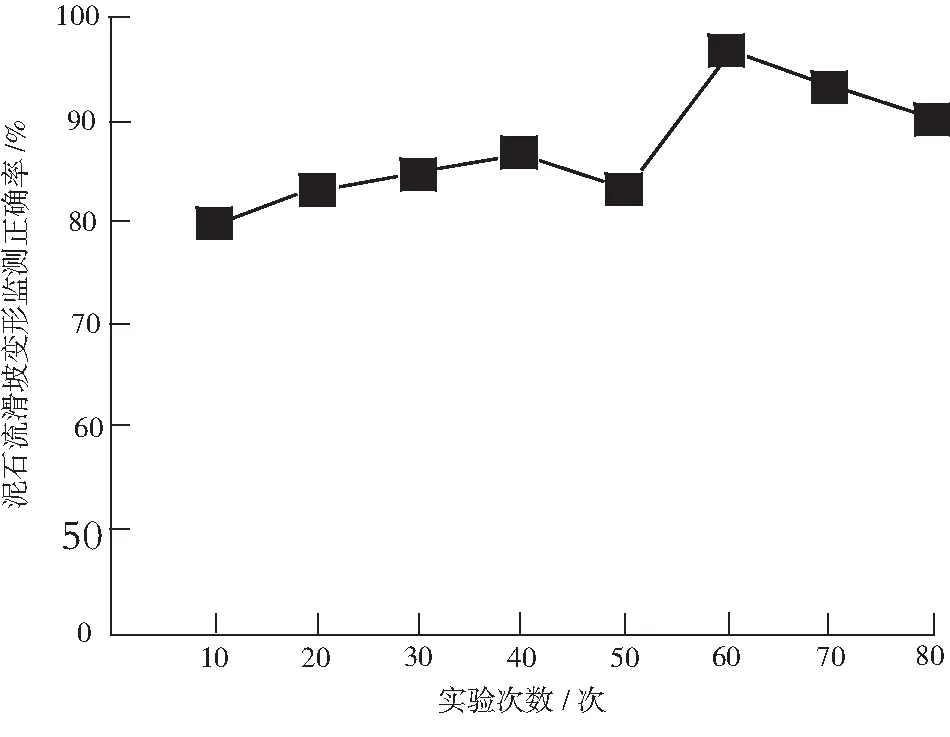
图2 滑坡变形监测正确率测试结果

分析图2所示结果可以看出，在对滑坡变形监测正确率测试时，发现8次实验中滑坡变形检测的正确率均在80%以上，第6次实验得到了监测正确率最高的结果，滑坡变形监测的正确率接近100%，该监测方法的正确性较好.通过对滑坡变形监测耗时和监测正确性的测试，证明了本文设计的基于数学形态学的滑坡变形自动化监测方法是可行的.

3 结束语

在对滑坡特征展开描述后，本文提出了基于数学形态学的滑坡变形自动化监测方法，并分别测试了滑坡变形监测的耗时情况和监测的正确率.实验结果说明，该方法不仅具有较短的监测耗时，还具有较高的监测正确率，验证了该方法的可行性和有效性.

尽管本文方法取得了一定的成果，但也存在很多需要改进和解决的问题.滑坡体十分复杂，一些研究具有较好的反演效果，监测结果存在或然性，滑坡变形监测工作任重道远.随着对滑坡变形监测的深入研究，监测结果将更加完善，从而降低滑坡自然灾害带来的危害.