一类二阶有理差分方程的渐近性行为
2022-05-31李丽丽
李丽丽
(山西应用科技学院 基础教学部,山西 太原 030000)
差分方程常用于模拟生物学、电子学、生理学、物理学、工程学和经济学等学科中出现的微分方程或时滞微分方程的离散模拟或数值求解,因此对差分方程的研究备受关注.尤其是对非线性差分方程解的行为的研究以及对平衡点的全局渐近稳定性的探讨更是激起了人们浓厚的兴趣.
Din[1]研究了一类二阶有理差分系统正解的定性性质
基于上面的研究,本文讨论另外一类二阶有理差分方程解的定性性质
(1)
其中,参数αi,βi,ai,bi,ci(i=1,2)和初值x0,x-1,y0,y-1都是正实数.本文首先研究了系统(1)的有界性和持久性,正平衡点的存在唯一性,正平衡点的局部渐近稳定性以及全局性,然后探讨了系统(1)的解收敛到其唯一正平衡点的速度.
1 有界性和持久性
对于系统(1),显然有下述结论成立.
引理1设(xn,yn)为系统(1)具有正初值x-1,x0,y-1,y0的解,则当n=1,2,…,时,恒有xn>0,yn>0成立.
关于差分系统
un+1=A1+B1υn -1,υn +1=A2+B2un -1,n=0,1,2,…,
(2)
其中,A1,A2,B1和B2均为正实数,有下面结论成立.
引理2设(un,υn)为系统(2)具有正初值u-1,u0,υ-1,υ0的解,则当n=0,1,2,…,时,恒有
证明用数学归纳法证明.显然,当n=0时结论成立.假设n=k-1时结论成立,则有
从而,当n=k时
u4k-1=A1+B1υ4k-3
v4k-1=A2+B2u4k-3
同理可以证明余下的等式成立.
推论1当B1B2<1时,系统(2)具有正初值u-1,u0,υ-1,υ0的解序列{un}和{υn}满足
推论2当B1B2<1时,系统(2)具有正初值u-1,u0,υ-1,υ0的解序列{un}和{υn}有界.
定理1表明了系统(1)正解的有界性和持久性[1-3].
定理1若β1β2 证明设{(xn,yn)}为系统(1)的具有正初值x-1,x0,y-1和y0的任一正解,则有 xn+1≤A1+B1yn-1,yn+1≤A2+B2xn-1,n=0,1,2,…, (3) 引进系统 un+1=A1+B1υn-1,υn+1=A2+B2un-1. {(un,vn)}是此系统具有正初值u-1,u0,υ-1,υ0的解,其中u-1=x-1,u0=x0,υ-1=y-1,υ0=y0,则对于任意的n∈N+,有xn≤un,yn≤υn. 事实上,n=1时,有x1≤A1+B1y-1=A1+B1υ-1=u1,y1≤A2+B2x-1=A2+B2u-1=υ1.假设对于n≤k-1,都有xk-1≤uk-1,yk-1≤υk-1.则当n=k时,有 xk≤A1+B1yk-2≤A1+B1υk-2=uk,yk≤A2+B2xk-2≤A2+B2uk-2=υk. 由推论1和推论2知,当B1B2<1时,即β1β2 从而有 (4) 由(1)和(4)得 (5) (6) 其中, 由公式(4)-公式(6),得 故定理得证. 推论4由定理1的证明及推论3知[L1,U1]×[L2,U2] 是系统(1)的正向不变集.即当初值x-1,x0∈[L1,U1],y-1,y0∈[L2,U2]时,恒有xn∈[L1,U1],yn∈[L2,U2]成立,其中n=1,2,…. 为了构造系统(1)相应的线性形式,考虑下面的变换 (xn,yn,xn-1,yn-1)|→(f,g,f1,g1), (7) 定理2若β1β2 (8) (9) (10) 则在[L1,U1]×[L2,U2]中系统(1)存在唯一的正平衡点. 证明考虑系统 (11) 设(x,y)∈[L1,U1]×[L2,U2],由(11)得 令 进一步,若公式(9)满足,有 因此,F(x)=0在区间[L1,U1]至少有一个正平衡点. 若公式(10)满足,有 故F(x)=0在区间[L1,U1]有唯一正平衡点. (12) (13) 令φ(λ)=λ4, 若(12)成立,设|λ|=1,则有 对于系统(1)的全局性有下面的结论[4]. 引理4假设f1∶[a,b]×[c,d]×[a,b]→[a,b],f2∶[a,b]×[c,d]×[c,d]→[c,d]是连续函数且满足下面的条件. (i)f1(x,y,z)关于y单调递增,关于x和z单调递减,f2(x,y,z)关于x单调递增,关于y和z单调递减. (ii)存在常数m1,M1,m2,M2, 当m1=f1(M1,m2,M1),M1=f1(m1,M2,m1),m2=f2(m1,M2,M2),M2=f2(M1,m2,m2)时,有m1=M1,m2=M2. 则差分系统 xn+1=f1(xn,yn-1,xn-1),yn+1=f2(xn-1,yn,yn-1) 证明令 且对每个i>0,构造 这样 即 即 这样 又 故有 由于对所有的n≥0,均有 这样,有 从而,对所有的n≥1有 进一步,当n≥1时,有 所以,当n≥2时,有 从而有以下性质. 令 则有 a≤m1≤M1≤b,c≤m2≤M2≤d. 由f1和f2的连续性,有 m1=f1(M1,m2,M1),M1=f1(m1,M2,m1),m2=f2(m1,M2,M2),M2=f2(M1,m2,m2). 所以 m1=M1,m2=M2. 定理4当β1β2 证明设 显然,f1∶[a,b]×[c,d]×[a,b]→[a,b]是关于y单调递增,关于x和z单调递减的连续映射.f2∶[a,b]×[c,d]×[c,d]→[c,d]是关于x单调递增,关于y和z单调递减的连续映射. 令(m1,M1,m2,M2)为系统 m1=f1(M1,m2,M1),M1=f1(m1,M2,m1),m2=f2(m1,M2,M2),M2=f2(M1,m2,m2) 的一个解,则有 (14) (15) 由(14)式得 m1[a1+(b1+c1)M1]=α1+β1m2, (16) M1[a1+(b1+c1)m1]=α1+β1M2. (17) 由(16)式和(17)式,有 a1(M1-m1)=β1(M2-m2). (18) 同理,由(15)式得 a2(M2-m2)=β2(M1-m1). (19) 由(18)式和(19)式,有 (20) 又由于β1β2 引理5[5]在定理3和定理4的条件下,系统(1)的唯一正平衡点是全局渐近稳定的. 本节讨论系统(1)的解收敛于其唯一正平衡点的速度[6]. 下面的结论说明了系统(21)解的收敛速度. Xn+1=(A+B(n))Xn, (21) 其中,Xn是m维向量,A∈Cm×m是常数矩阵,B(n)∶Z+→Cm×m是矩阵函数且满足 (22) 命题1[1]假设公式(22)满足,Xn是系统(21)的解,则对任意的n有Xn=0或者 (23) 存在且等于矩阵A的一特征值的模. 命题2[1]假设条件(22)满足,Xn是系统(21)的解,则对任意的n有Xn=0或者 (24) 存在且等于矩阵A的一特征值的模. 设{(xn,yn)}是系统(1)的任一解使得 其中 为了计算误差,由系统(1)得 其中, 误差项的限制系统为 定理5设{(xn,yn)}是系统(1)使得 成立的正解,其中 定理6若β1β2<α1α2,则系统(1)存在素二周期解. 证明利用反证法.假设系统(1)存在素二周期解 …,(p1,q1),(p2,q2),(p1,q1),… 其中,p1≠p2,q1≠q2,且对i∈{1,2},pi,qi是正实数,则由系统(1)得 (25) (26) 由公式(25)和公式(26)得 (27) (28) (29) (30) 由公式(27)和公式(28)得到 (p1-p2)[a1+c1(p1+p2)]=β1(q1-q2). (31) 由公式(29)和公式(30)得到 (q1-q2)[a2+c2(q1+q2)]=β2(p1-p2). (32) 由公式(31)和公式(32)得到 (33) 若β1β2
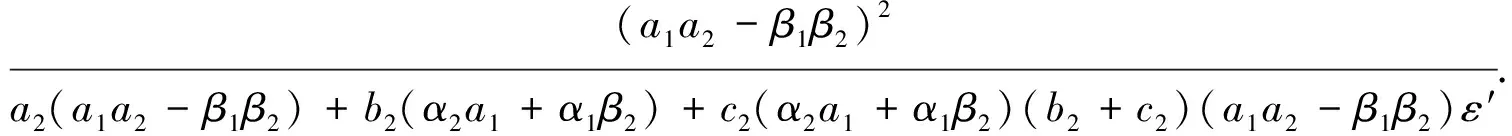
2 稳定性

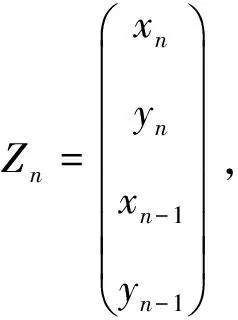
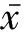






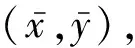
3 收敛速度
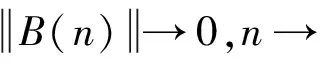

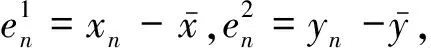
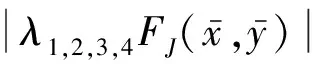
4 周期性
