基于多项式曲线拟合的海上地震勘探拖缆定位

余文坤，吴佩达，张昊楠，胡广浩，阮福明，戴吾蛟，匡翠林

1. 中南大学地球科学与信息物理学院，湖南 长沙 410083； 2. 中海油田服务股份有限公司物探事业部，天津300451； 3. 海洋石油勘探国家工程实验室，北京100028

石油、天然气是重要的燃料和化工原料，发展海洋定位导航技术有利于提高我国的油气勘探水平，关系到国家能源安全和海洋战略部署[1]。海上拖缆地震勘探技术是目前世界上主流的海洋油气勘探技术之一，其作业过程为：物探船拖曳若干条水下电缆，利用电缆上的检波器探测由模拟震源(空气枪等)激发并从海底反弹的地震波，经过数据分析估计出海底的油气储藏[2-4]。其中，拖缆定位的任务是融合拖缆系统搭载的多种导航传感器数据计算检波点坐标，而高精度的检波点坐标是事后分析地震勘探结果的重要保障[5-6]。然而，海洋勘探导航定位市场长期以来被几家国外物探公司研发的导航系统所垄断，包括美国ION公司的Orca系统、法国Sercel公司的SeaPro系统等[7-9]。

发展自主的拖缆导航定位系统，需要研发高精度电缆定位算法。现有拖缆定位通常采用数值方式实现[10]，其中单缆定位的基本流程为：从电缆一端基准点出发，通常是尾标点或者声学节点，采用类似导线测量的方式基于距离和方位角(内插或拟合得到的)沿电缆递推得到各点坐标，最后根据另一端的基准点对积分导致的坐标误差进行整体修正，例如旋转、平移和缩放。多缆定位时则采用网平差和曲线积分相结合的方法，先对声学网进行边角网或测边网平差得到高精度的声学节点坐标，然后沿曲线积分确定声学节点之间的检波点坐标，并以声学节点为基准改正曲线积分的误差累积效应。数值方法比较灵活，其根据所选的具体模型有许多变种，不同模型适用于不同的拖缆系统配置，但是难以得到严密的平差和精度评定结果[6]。国内学者自20世纪90年代末开始对电缆定位的模型和算法开展了大量卓有成效的研究。文献[11]较早地研究了海上拖缆地震勘探中单缆和多缆定位的原理，指出单缆定位类似导线平差，而多缆定位类似声学节点的网平差，区别是声学网络一般只覆盖电缆的前部、中部和后部。文献[12]指出在电缆坐标递推过程中，基于弧段、多项式和曲线积分3种电缆形状模型(其分别假设电缆的基本组成为圆弧、多项式曲线和折线)都能满足定位精度需求，其中多项式模型建立的是电缆偏移量与切线方位角的函数关系[13]，不能直接得到电缆上的点坐标。基于曲线积分模型的算法是国内学者们的主要研究对象，由于观测值含有误差，曲线积分将出现坐标误差的累积，因此要求积分步长较短，通常先按照检波点积分(间隔约12 m)，再以高精度节点为基准对坐标结果进行修正。文献[14]以尾标点为基准调整曲线积分的结果。文献[15]以测边网平差的声学节点的坐标为基准调整曲线积分结果，再以多项式曲线拟合声学节点坐标确定电缆形状。文献[16]以Kalman滤波得到的声学节点坐标为基准线性加权得到检波点坐标。文献[14—16]对曲线积分的结果做了一次调整，文献[12]则提出进行两次曲线积分和调整的方法。文献[17]提出了“约束网平差、曲线积分、拟稳平差”的定位策略，在前、后声学网平差调整曲线积分结果的基础上再利用中网拟稳平差进行缆形调整。多次调整的定位方案精细化了计算步骤，但仍属于近似计算，无法完全保障结果最优。

拖缆定位算法的另一种形式是解析方式，通过直接构建观测值与电缆上点坐标的函数关系平差获得电缆上点的坐标。解析方式可以获得理论最优解且便于质量控制[18]，但可能存在稳定性和求解复杂性问题。文献[5]提出一种曲线拟合模型统一表达所有观测值，然而由于其模型采用了三角函数和多项式曲线相乘的形式，计算过程较为复杂，因此没有引起学者和生产单位的广泛应用。文献[19]提出直接建立拖缆航向垂直位移与沿电缆偏移量的多项式函数，利用方位角观测平差估计多项式系数，但未考虑声学观测和多缆定位的情况。

针对现有方法存在对观测值利用不够充分、观测数据平差建模不够严密，计算步骤繁多，复杂度高等问题，本文提出一种多项式曲线拟合的解析定位模型，充分利用导航观测数据进行严密平差，并使用实测数据进行了有效性验证。研究结果可为发展我国自主的拖缆定位方法和软件提供有益参考。

1 基于多项式曲线的电缆定位平差模型

1.1 数学模型

海上拖缆系统一般使用3～12 km长的电缆[2]，电缆在地震勘探过程中呈现为较为光滑的曲线[20]，可使用多项式对其形状进行拟合。如图1所示，将电缆上任意点的坐标(x,y,z)视为沿电缆的偏移s为自变量的多项式函数。

图1 曲线拟合电缆定位模型Fig.1 Curve-fitting-based streamer positioning model

通常电缆拉伸已经被精确测量并考虑进偏移值，s被认为在勘探过程中保持不变，则电缆上i点的坐标与其曲线偏移si的函数关系可表达为

(1)

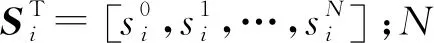
1.2 观测值及观测误差方程

海上导航定位的主要传感器包括差分全球定位系统(differential global positioning system，DGPS)、电罗经、深度计、相对GPS(relative GPS，RGPS)、声学鸟和罗经鸟[21]。DGPS和电罗经安置于拖缆船上，分别引入地理坐标系下的高精度绝对位置和船头方位角，DGPS位置包含经纬度和大地高或海拔高，精度一般为分米级。拖缆船被假定为刚体，设备间相对关系固定，因而可推算得到船上其他点位的坐标(忽略物探船姿态的影响或者使用惯导加以考虑)。深度计测量传感器的水下深度，布设在电缆和枪阵上，枪阵因此兼有两种高程，从而统一整个拖缆系统的高程。RGPS测量两点间的距离和真方位角，其将绝对位置从物探船传递到位于枪阵和电缆前/后的浮标上(即头/尾标)。声学鸟和罗经鸟分别提供两点声学距离和电缆切线磁方位角，利用边和角的观测实现坐标信息在电缆上的传递。实际计算时，采用以船参考位置为原点的站心坐标系，再利用船参考点与DGPS点的相对关系实现与地理坐标的转换。

为求解多项式曲线模型，需要建立罗经鸟方位角、声学距离等观测值与多项式曲线系数之间的数学关系。以下给出这些观测的具体函数形式。

(1) 坐标观测值

ri=f(si)

(2)

式中，ri为i点的坐标向量；si为i点在电缆上的偏移。

(2) 声学距离观测值

同缆声学距离观测值(同一电缆的i点与j点)

(3)

式中，di,j为同缆上i点与j点之间的距离观测值；si和sj分别为i点与j点对应的沿电缆偏移。

异缆声学距离观测值(G缆i点与F缆j点)

(4)

式中，dGi,Fj为G缆i点与F缆j点之间的距离观测值；si和sj分别为i点与j点对应的沿电缆偏移。

(3) 方位角观测值(预处理时已进行磁偏角改正)

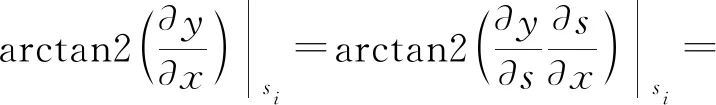
(5)

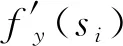
(4) 深度观测值

hi=-fz(si)

(6)

式中，hi为i点在水下的深度观测值。

令A0、B0、C0为电缆x、y、z坐标分量对应的待估参数近似值，δA、δB、δC为相应的参数改正数，在近似值处对以上观测值做泰勒一阶展开，推导得到对应误差方程如下。

(1) 坐标观测值误差方程

(7)

式中，lxi、lyi、lzi为常数项。

(2) 声学距离观测值误差方程

将式(1)代入式(3)可得

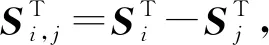
(8)

同理，可得异缆声学距离观测误差方程(G缆i点与F缆j点)

(9)

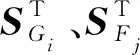
(3) 方位角观测值误差方程

由式(5)和式(1)可知

式中，H=[0,1,2s1,…,NsN-1]。再根据反正切函数的微分公式

易推导得到

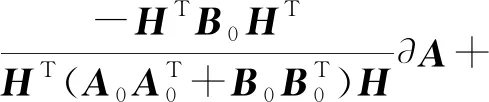
(10)

式中，lαi为常数项。

(4) 深度观测值误差方程

(11)

式中，lhi为常数项。

1.3 模型系数估计

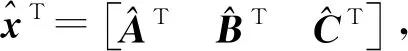
(12)

1.4 模型分析

相比于基于曲线积分的传统定位模型[16]，基于曲线拟合的本文模型在理论上更加严密，电缆定位网络中的观测值都能够得到直接表达，且待估参数显著减少。假设有一个三维n缆系统，每条缆上有声学节点m个，本文模型和传统模型需要估计的参数个数Tnew和Told分别为

(13)

式中，N为曲线模型的阶数；Tnew与Told的比值为(N+1)/m，因此电缆上的声学节点数m越大，本文模型的优势越明显。另外，曲线拟合之后能够直接获得电缆上任意点的坐标。以检波点为例，传统方法计算检波点时，首先使用曲线积分模型推算其坐标，然后以平差后的声学节点坐标为基准做调整，而本文模型只需将检波点的沿电缆偏移s代入式(1)即可求得其坐标。

2 算例结果与分析

海上地震勘探测线一般在工作海域布设成互平行的直线，物探船沿着测线逐条作业，拖缆定位为物探提供基础位置信息。为验证曲线拟合定位模型的实际效果，使用2019年我国南海某工区7条测线的实测数据，测线方位角约为290°，每条测线的时间跨度约6 h，包含约1600炮数据，响炮间隔约13 s，每次响炮时触发传感器网络的定位解算。由于海上地震勘探过程中电缆在海水中的深度较为稳定[24]，深度观测的精度相对较高，因此有时只对平面坐标进行估计。传感器网络具体配置见表1，图2为相应的示意图，其中物探船搭载DGPS、电罗经和参考RGPS传感器，船体拖曳两个枪阵，每个枪阵上挂载3个RGPS，共有6条电缆，每条电缆长度约7 km，电缆尾部的浮标上皆挂载1个RGPS，声学网络为前后型声学网络，声学前网有12个声学节点，声学后网有72个声学节点。

表1 实测数据硬件设备配置信息

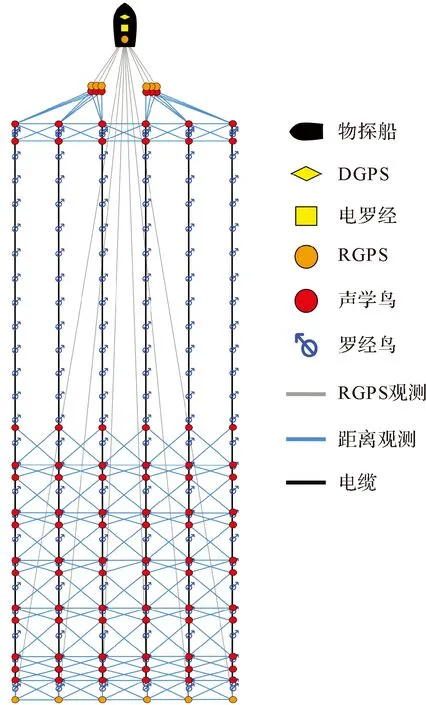
图2 海上地震勘探6缆定位网络Fig.2 Six-streamer positioning network for marine seismic exploration

测试过程中，多项式曲线使用5阶，并且对多项式系数估值做显著性检验，删除不显著的系数，由于电缆长度较长，观测数据量丰富，计算过程中未发现明显的虚假参数。

由于海上地震勘探难以获得电缆网络的真实坐标，因此，将国际商业软件系统Orca解算的检波点坐标作为参考值。将计算的检波点坐标转换为通用横轴墨卡托(universal transvers Mercator，UTM)投影下的平面坐标，考虑到物探作业更关心绝对的坐标误差，所以本文采用以下偏差公式作为模型精度评定的标准

(14)

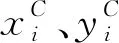
(15)

式中，biasDA和biasDC分别为偏差bias在DA和DC方向的分量；β为测线方位角。

以7号测线数据为例详细分析算法的定位性能，其他数据的结果与7号线类似，只以统计的形式在表4给出。图3和图4分别给出了电缆上所有检波点坐标偏差均值及其DA、DC分量的时间序列，可以看到，传统模型在0～1200炮之间坐标偏差在6～14 m范围内变化，1200炮之后坐标偏差稳定在4～6 m范围内。DC方向的偏差明显大于DA方向偏差，如图4所示，这是因为DC方向易受洋流影响产生扰动，并且由于电缆受拖缆船牵引，DA方向的波动性要小于DC方向。本文模型显著减小了坐标的偏差和波动，其偏差值在4 m左右，波动程度优于1 m，见表2。相比于传统模型，本文模型使得定位偏差减小了53.6%，其中DA和DC方向分别减少了51.0%和54.7%。在标准差方面，本文模型的偏差值序列的标准差为0.68 m，较传统模型减小了74.5%，其中DA和DC方向分别减少了57.9%和73.7%，说明曲线拟合定位模型定位性能更加稳定。本文模型的优势在最大值和最小值方面也得到了体现，传统模型的坐标偏差变化范围为14.43～2.57 m，而曲线拟合定位模型则表现出较小的偏差值变化，其偏差值范围缩小为7.17～2.15 m。

表2 检波点偏差统计结果

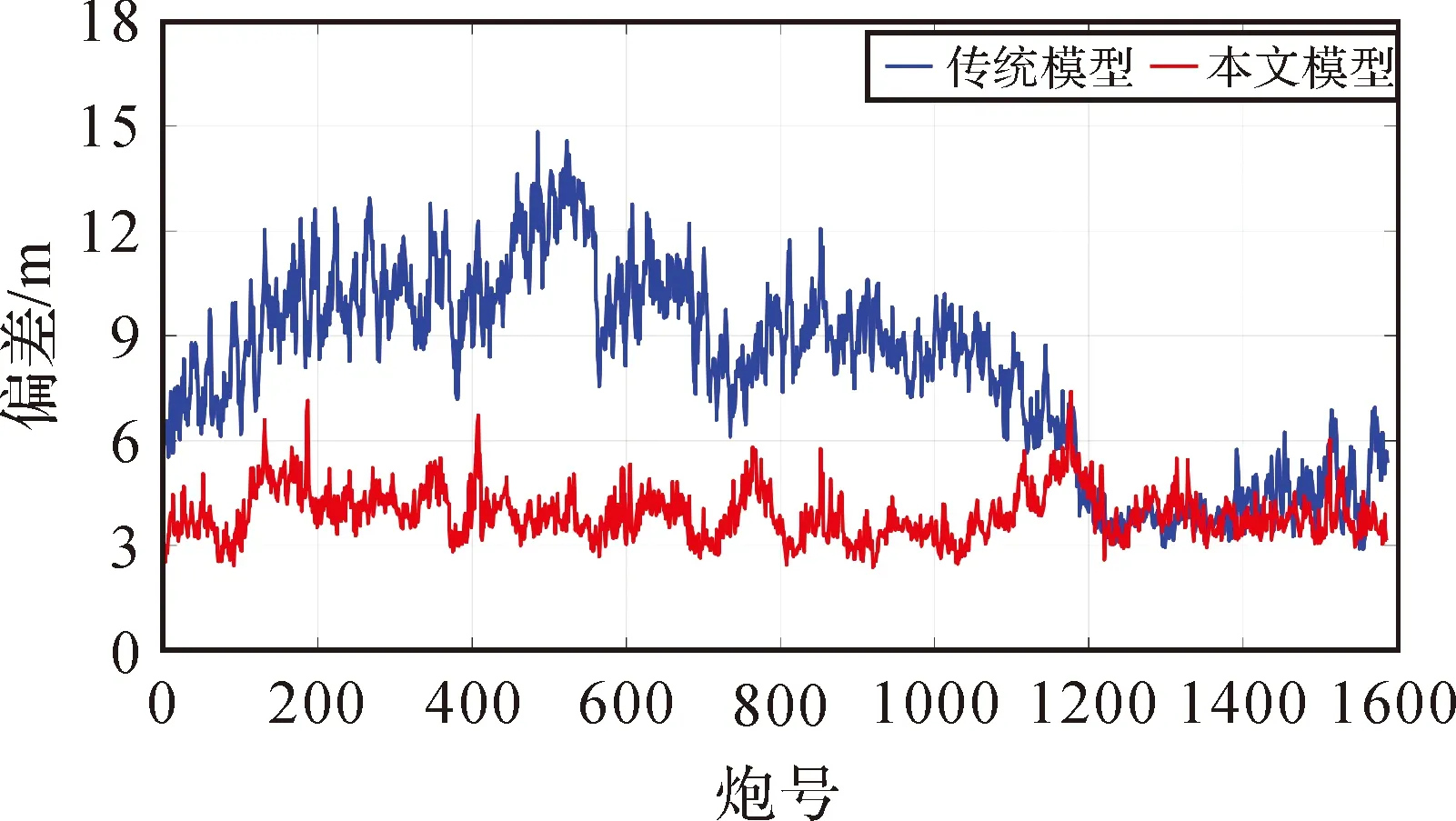
图3 检波点偏差序列Fig.3 Bias of receiver points

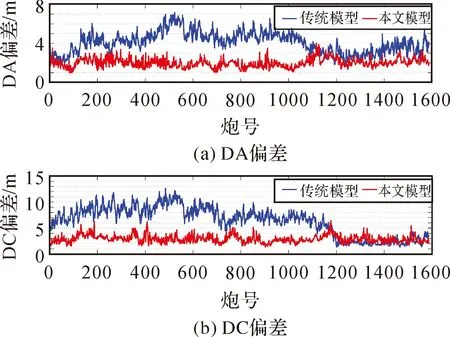
图4 检波点DA偏差和DC偏差Fig.4 DA and DC bias of receiver points

在测试数据中，后部第1排声学鸟偏移量约3.7 km，以此为分界线将电缆分为前、后两部分。由于电缆两端靠近RGPS点(即前部枪阵RGPS点、尾部浮标RGPS点)，且通常布设了声学网络，因此理论上越靠近前后端的检波点的坐标精度越高。图5显示了电缆上不同偏移的检波点的偏差均值曲线，可以看出传统模型的检波点DA偏差峰值在电缆前部和中部，DC偏差峰值在电缆中部。图5中黑色竖线为电缆前网与电缆后网的分界线。传统模型在电缆中部出现偏差值的峰值，说明误差通过传播积累在电缆中部，而电缆头部DA偏差出现峰值，说明旋转调整会给误差的传播带来不确定性。相比之下，本文模型计算的检波点偏差整体较小，曲线更光滑，中部没有明显的偏差累积，偏差最大值出现在电缆前网的中部。这说明使用曲线拟合定位模型通过观测值网络可以较好地将电缆尾部的基准传递到中部，而前网中部的检波点距离前、后声学网络距离最远，所以其偏差值最大。图6给出了各电缆检波点的DA和DC偏差曲线，可以看出传统模型电缆后部的偏差值曲线变化趋势一致，各条曲线基本吻合，但电缆前部的DA偏差曲线差异较大，且各条曲线的变化趋势也不完全相同。相比之下，曲线拟合模型各条偏差曲线基本吻合，电缆前部的偏差曲线间的差异较小，整体变化趋势相同，说明曲线拟合模型各条电缆解算结果的精度比较一致。

图5 电缆检波点偏差均值Fig.5 Average bias of receiver points of streamers

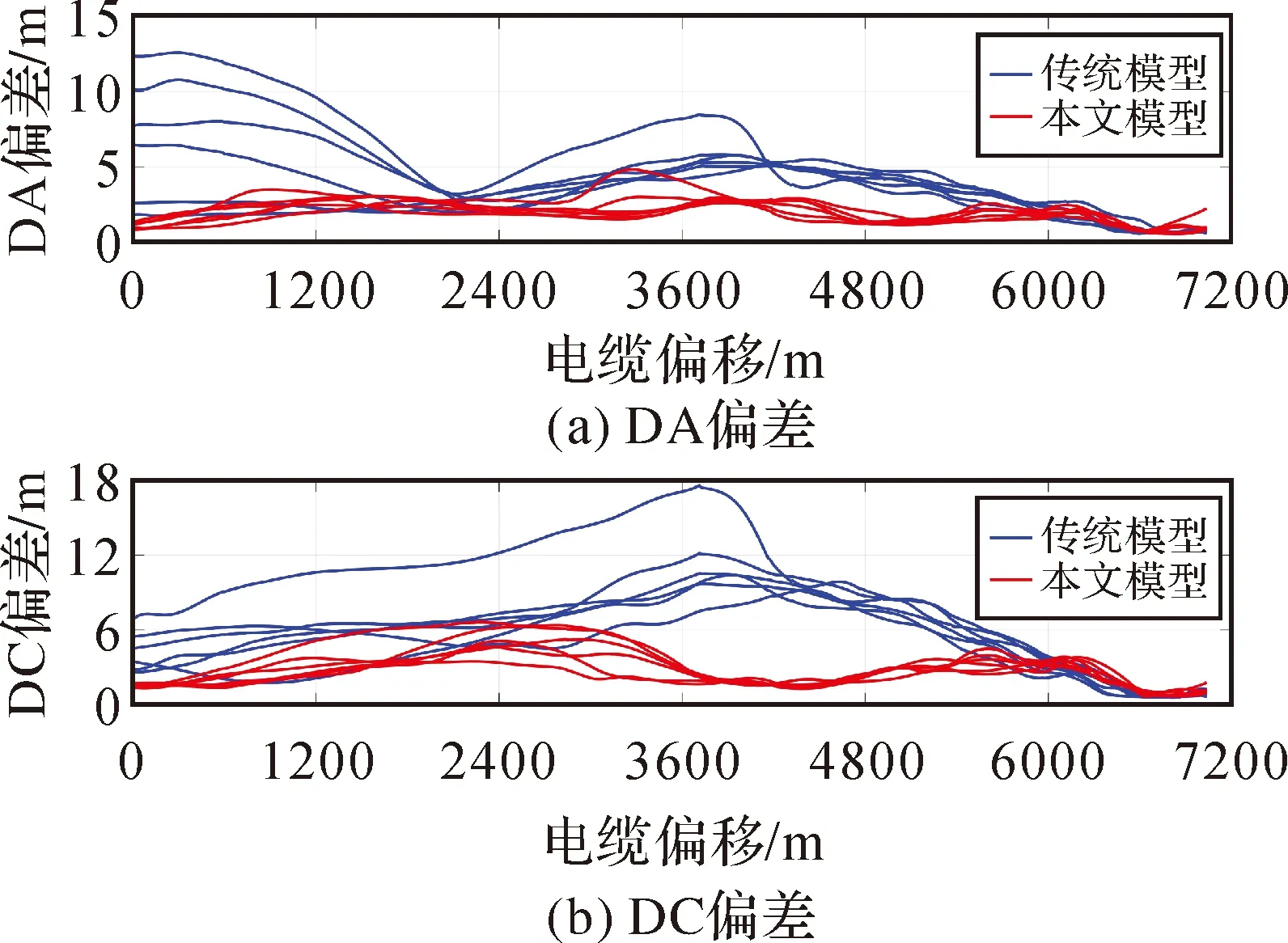
图6 不同电缆的检波点偏差Fig.6 Bias of receiver points of different streamers

图7比较了电缆不同部分检波点的偏差值均值，具体数值见表3，相对传统模型，本文模型的前、后网检波点偏差均有明显改善，其前网DA和DC偏差值均值分别减少54.0%和50.1%，后网检波点DA和DC的偏差值均值分别减少46.1%和60.8%。另外，本文模型和传统模型在DA和DC方向的偏差均是后网优于前网，说明二者通过对声学后网的平差均使声学后网的精度得到了提高。

表3 电缆前网和后网检波点DA偏差和DC偏差统计

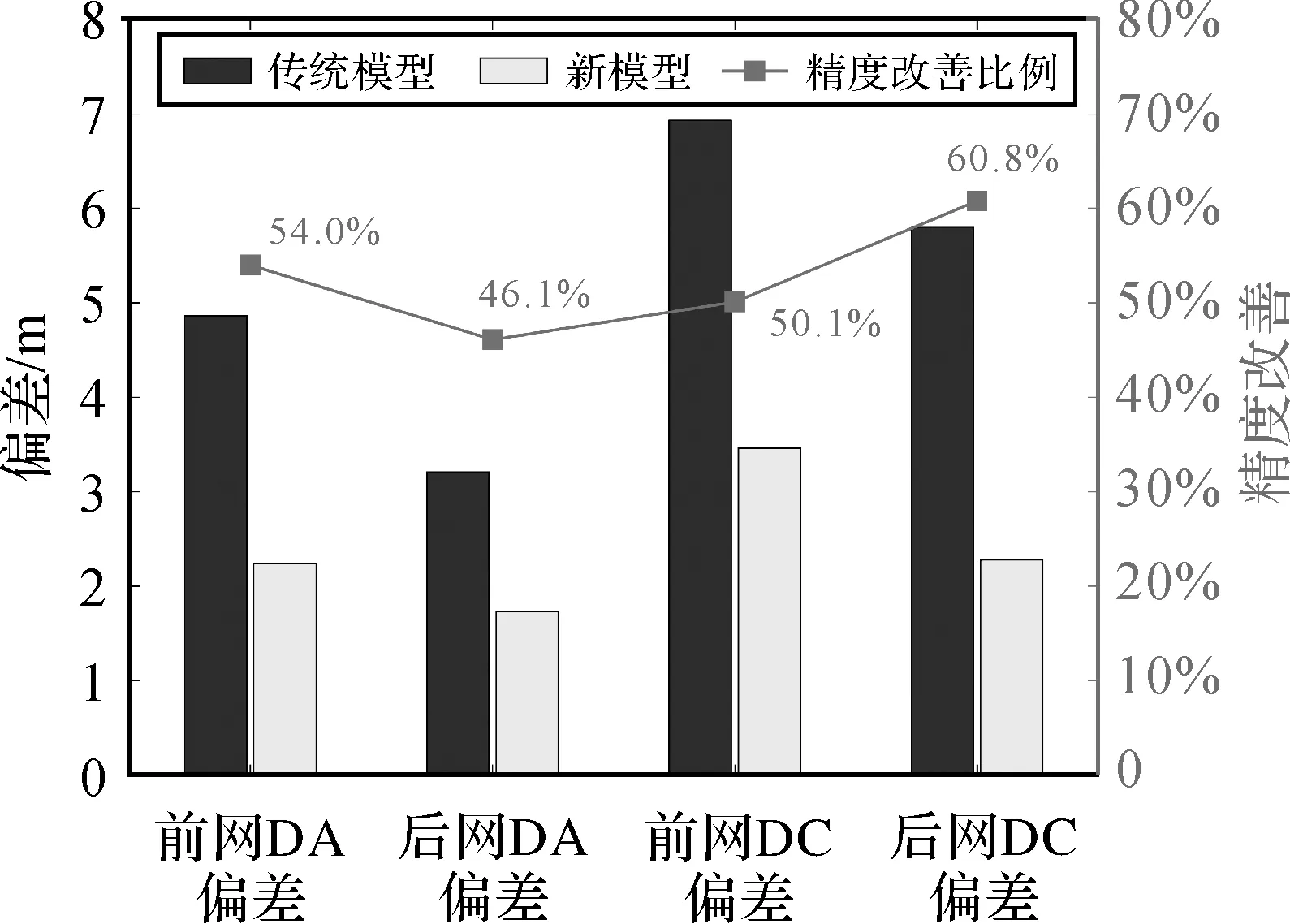
图7 电缆前网和后网检波点DA偏差和DC偏差对比Fig.7 Comparison of DA bias and DC bias of receiver points in the front net and rear net of streamers

以7号测线S1电缆为例，图8和图9分别显示不同电缆偏移位置的罗经鸟和声学距离残差分布，可以看出方位观测值和距离观测值的残差均较好地服从正态分布。图9中，S1A1—S2A1等为声学观测标识，它表示S1电缆A1声学鸟与S2缆线A1声学鸟间的声学距离。对于方位观测值， 靠近电缆前部的观测残差分布更为集中，中、后部的观测表现出一定的偏差，而距离观测值则都含有不同程度的偏差。这些观测偏差可能来源于磁偏角改正误差、动态声速值误差、设备误差、曲线模型误差等，后续对这些系统误差更加深入地研究和处理(例如设备检校、模型补偿等[10,25-26])有望进一步提高定位精度。

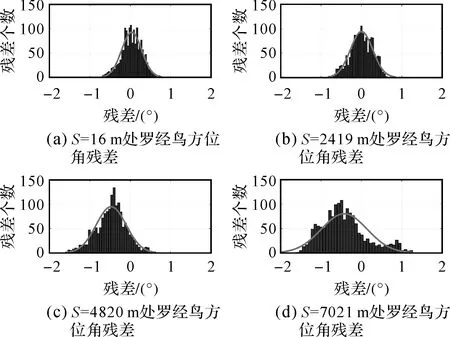
图8 电缆上不同偏移的罗经鸟方位观测值残差分布Fig.8 Residual distribution of compass azimuth observations with different offsets

图9 电缆上不同偏移的声学鸟距离观测值残差分布Fig.9 Residual distribution of acoustic range observations with different offsets

表4给出了算例中7条测线所有电缆检波点的坐标误差统计结果，可以看出，本文模型的偏差值最大值和最小值分别为5.36 m和3.52 m，较传统方法的精度改善比例最小为21.7%，最大为58.1%；传统模型的偏差值均值为7.41 m，本文模型的偏差值均值为4.42 m，因此，本文模型的精度总体上优于传统模型。

3 结 论

高精度电缆定位算法是海上拖缆勘探导航系统的核心。为解决传统定位算法因数学严密性不足、计算过程复杂而限制电缆定位精度的问题，本文结合海上拖缆勘探过程中电缆呈光滑曲线的物理特性和定位网络观测数据的特点，提出了一种基于曲线拟合的电缆定位模型，通过严密平差实现了对所有观测值的充分利用。基于我国南海区域的实测数据试验表明，本文模型可获得约4.5 m的检波点定位精度，与传统方法相比精度改善率可达58.1%，且定位性能更加稳定、更加高效，能够更好地满足海上拖缆地震勘探电缆定位的需求。

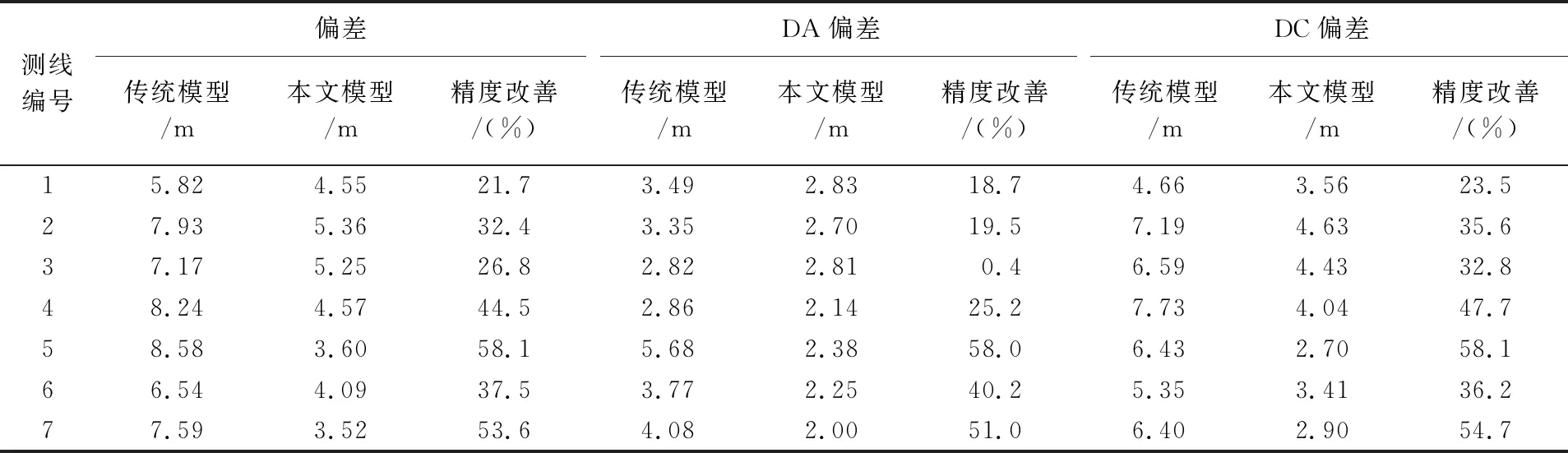
表4 实测数据测试结果统计表