多波束测深误差改进模型构建与验证

1 多波束测深点位置归算模型

1.1 Rob Hare测点位置归算模型

Rob Hare模型是研究多波束测深各误差源影响量级分析的经典位置归算模型，其基本思想是按坐标旋转的方式构建测深中心与测深点之间的关系模型。即首先建立以接收换能器几何中心为坐标系原点的船体坐标系(载体固联坐标系)O→(X,Y,Z)和当地水平坐标系(LLS)O→(XLL,YLL,Z)，各坐标轴指向如图1所示。设波束指向角为θ0(波束方向与换能器平面垂向夹角)，r为θ0方向上测得的斜距。姿态测量横摇角roll为R(左舷向上为正)、纵摇角pitch为P(船艏向上为正)、航向角为A(艏摇yaw方向相同)，在船体坐标系下，测深点q的坐标(xq,yq,zq)，在当地水平坐标系(LLS)下，经动态偏心改正(ΔXat,ΔYat,ΔZat)，设定位设备中心在船体坐标系中的坐标为(xa,ya,za)，则测深点q的坐标(xlq,ylq,zlq)表示为

(1)

然而由于海水温度、盐度等分层不同，声波在海水中实际传播路径为一条曲线，直接的坐标旋转将引入误差，为了精确获取测深点位置，精确计算横纵摇影响下波束入射角，通常采用常梯度声线跟踪模型归算测点位置。为此，本文采用常梯度声线跟踪模型进行测点位置归算。

1.2 常梯度声线跟踪测点位置归算模型

常梯度声线跟踪模型的原理是根据波束的指向角和往返传播时间，逐层跟踪测深点相对换能器中心的水平距离和水深。如图1所示，考虑到测船姿态的影响，在当地水平坐标系下，该波束与Z轴的夹角为θf(波束的实际指向角)，与X轴的夹角为φf，则

(2)

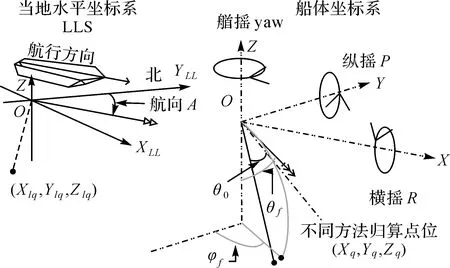
图1 当地水平坐标系(LLS)及波束实际入射方向Fig.1 Local level System and Beam actual incident direction

假设声速剖面数据已知，即可通过单个波束回波时间根据已知声速剖面应用常梯度声线跟踪公式[15]。设该波束到海底共经过n层(第n层未全部跟踪时单独作为一层),声波入射时声速为Cvs，Snell常数p=sinθf/Cvs，可得式(3)

(3)

式中，ri为每层声波传播距离；Ri、Li分别对应其曲率半径和水平位移。若将声线每层圆弧路径的微分单元近似取为其对应的弦长，并结合每层精确波束入射角θi，则可计算声线在整个水柱中的垂直位移。则在船体坐标系中海底点(xq,yq,zq)的坐标表达式为

(4)

船体坐标系下水深点坐标(xq,yq,zq)可以换算到当地水平坐标系下的坐标(xlq,ylq,zlq)，表示为

(5)

2 多波束测深误差改进模型

为了更加系统地评估各项误差源对测深点的影响方式和影响规律，本文按条带型误差源和单个波束型误差源对多波束测深垂直误差和平面误差的来源进行了系统的区分，如图2、图3所示，并建立了相应的误差改进模型。

2.1 垂直方向误差源及其改进模型

如图2所示，蓝色项表示改进模型与Rob Hare模型相比改进较大项：对于单个条带而言，多波束测深误差主要由水位改正、吃水改正和升沉改正引起，考虑到升沉和吃水改正中，误差对测深点的影响与其声线跟踪起算面相关，对垂直方向误差贡献量呈系统性，改进模型对此综合分析；对于单个波束而言，可分为与回波时间(TOA)相关和回波角度(DOA)相关的误差贡献量，改进模型考虑了不同检测方式(振幅法/相位法)引起的误差；由于常梯度声线跟踪算法引入，求解声速剖面误差导致误差采取逐层累加的方式，相比于Rob Hare模型的近似计算方法改进较大。

绿色项为考虑常梯度声线跟踪公式更新项：对表层声速误差导致的测距和测角误差和横、纵摇测量误差及安装偏差误差引起的误差公式进行更新。改进模型与Rob Hare模型相比更贴近实际测量情况,误差构成更加完善。

根据误差传播定律，可由(4)式得到水深的累计误差σd，表示为

(6)

进一步，假设各角度和距离误差相互独立且服从正态分布，各因素对测深误差的影响分析如下。

(1) 测距误差。多波束测深系统由测距误差σrm引起的垂直方向误差大小也与声速剖面测量误差σcm有关，用rm和Ci表示该波束声线传播距离和第i层声速，则测距误差的影响量σd1可表示为

(7)

然而，由于振幅检测法(amplitude detection)和相位检测法(phase detection)检测原理和导致的误差大小不同，分别给出计算式(8)[7，16]，同时考虑到实际测量时，存在参数记录不完全的情况，也可以用代表性测距误差σrm_means近似计算

(8)

式中，σrm_amp、σrm_pha为振幅检测和相位检测测距误差；c为常声速1500 m/s；采样分辨率Δrs=c/2f，通过模拟信号与数字信号转换采样率f求得；τ为发射波束脉宽；Ψy为接收波束角；nA为振幅检测采样数。

(2) 波束指向角误差(包含横摇误差)。σRm与σΔR表示运动传感器的横摇角R测量误差和稳定性试验的未校准误差(安装偏差误差)。波束指向角对测深误差贡献量σd2可表示为

(9)

式中，σθm为波束指向角测量误差，根据检测方式不同求出，考虑到实际测量时，存在记录不完全的情况，以代表性测角误差σθm_means计算[7-16]

图2 多波束测深垂直误差源分类及改进Fig.2 Classification and improvement of vertical error sources in MBES

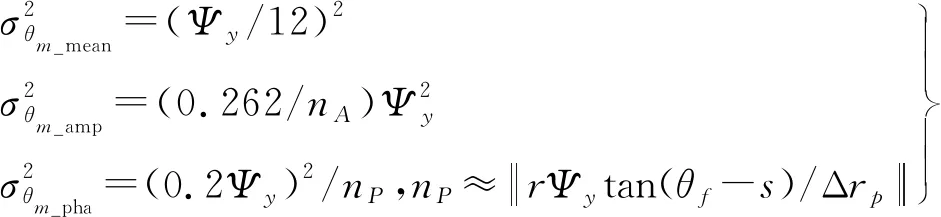
(10)

式中，nP为相位检测数；s为测点斜率；Δrp为相位检测采样率，通常情况与Δrs相等。

(3) 纵摇角误差。σpm、σΔP表示运动传感器的纵摇角P测量误差和稳定性试验的未校准误差(安装偏差误差),则纵摇角误差对测深误差的贡献量σd3为

(11)

(4) 波束角误差。Ψx表示发射波束开角的大小，波束角误差对测深误差的贡献量σd4表示为

(12)

(5) 声速误差。σθvs为表层声速测量误差，对表层声速测量误差加以区分，则声速误差对测深误差的贡献量σd5表示为

(13)

(6) 升沉误差。由图2可知，多波束换能器实时升沉H由该时刻姿态传感器的测量升沉值Hm(real heave)和诱导升沉Hi组成

(14)

式中,a为升沉标称精度中的固定部分；(b×heave)为其可变的部分。而对于诱导升沉而言，根据误差传播律可得

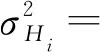
(15)

值得注意的是，根据多波束测深测点归算作业流程，升沉误差对测深点的影响呈系统性，体现在入射深度上进而影响最终声线跟踪归算测深点深度，由此给出总升沉误差对测深误差贡献量σheave为

(16)

若使用的升沉测量设备有延时升沉(delayed heave)计算功能，使用计算的真升沉值(true heave)进行跟踪归算，可减少实时升沉误差，以POS MV WaveMaster Ⅱ为例，其精度可以达到0.01 m。

(7) 吃水误差。draught表示测船静止时的吃水，squat表示测船航行时，由于船速造成的吃水的改变，load为在航行中，由于油料消耗等原因造成的测船吃水的改变与升沉误差影响方式相同，其总吃水误差对测深误差贡献量σdyn_draught为

(17)

(8) 水位误差。多波束测深数据处理时，由于水位改正在声线跟踪之后进行，考虑到水位误差与升沉改正和吃水改正存在误差的影响方式不同，可以直接确定其影响，其中可以分为潮位测量误差、潮位控制误差和垂直基准误差，总体用σWL表示。

(9) 总测深误差

σdepth=

(18)

2.2 水平方向误差源及其改进模型

如图3所示，蓝色项表示改进模型与Rob Hare模型相比改进较大项：对于单个条带而言，多波束水平方向误差主要由水平定位误差、坐标动态偏心改正误差引起，与垂直方向误差类似考虑到升沉和吃水改正对其声线跟踪起算面影响，进而系统性影响水平位置归算，改进模型对此综合分析；对于单个波束而言，水平方向误差可分为与回波时间(TOA)相关和回波角度(DOA)相关的误差贡献量。改进模型同样顾及检测方式应用式(8)和式(10)，改进水平方向的误差贡献量；由于引入常梯度声线跟踪算法，采取逐层累加的方式求解声速剖面误差导致误差，相比于Rob Hare模型的近似计算方法改进较大。

绿色项为考虑常梯度声线跟踪公式更新项：在水平方向上表层声速误差导致的测距、测角误差，横、纵摇测量误差和安装偏差误差。

根据式(4)利用误差传播律，则船体坐标系下水平方向累计误差σh和动态偏心改正在水平方向上误差σΔat

(19)

式中，以σ0表示定位设备自身误差；σX_at、σY_at和σx_tq、σy_tq分别表示动态偏心改正和船体坐标系下水平位置归算误差。各误差分量表示如式(20)所示

(20)

式中，σAm、σΔA分别是运动传感器的艏摇角测量误差和稳定性试验的未校准误差(安装偏差误差)。结合式(19)、式(20)，则可以得到总的平面中误差可表示为

(21)

3 试验分析

3.1 数据准备

数据选取2020年6月大连某地实测数据。多波束测深仪采用Reson T50-P，定位定姿系统采用POS MV WaveMaster Ⅱ，声速测量使用AML Minos·X声速剖面仪。根据仪器标称精度和偏差校准经验，给出模型涉及的各误差源数值大小见表1。

表1 多波束测深系统主要误差源参数

选取本次测量1、2号交叉测线，应用常梯度跟踪模型，经过标准水深处理改正流程获得航迹线、水深如图4所示，水深范围17.8～19.5 m。

图3 多波束测深水平方向误差源分类及改进Fig.3 Classification and improvement of horizontal error sources in MBES

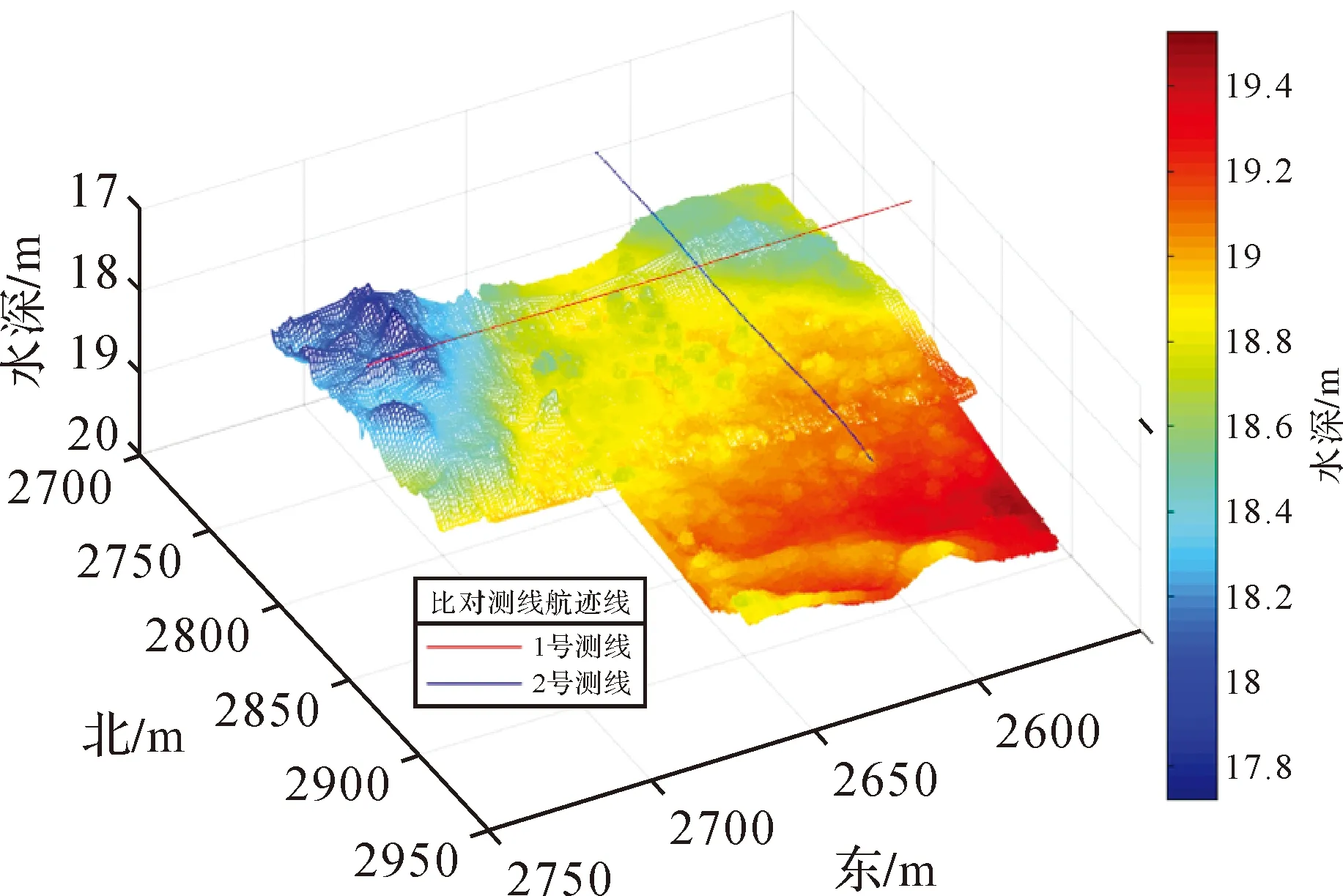
图4 1、2号比对测线水深Fig.4 The comparison chart of the water depth map of 1 and 2 survey line

3.2 测深误差模型对比分析

改进模型正确性验证。将表1误差值分别代入改进模型和Rob Hare模型，其中测角和测距误差改进模型应用式(8)、式(10)中精确计算各方向误差贡献量，Rob Hare模型应用其代表性误差，其目的是减小误差值选取对模型比对的影响，计算1号测线上测深点垂直和水平中误差如图5所示。由图5可以看出以下规律。

(1) 在垂直和水平方向两个模型的波束误差分布趋势相同，总体呈中央波束误差小，边缘波束误差大的特点。

(2) 在垂直方向上，如图5(a)所示，改进模型误差中央波束小于Rob Hare模型误差，且改进模型分布不规律。原因在于改进模型考虑不同回波检测方式对测深误差的影响规律，中央波束附近采用振幅检测，其波束测距误差引起测深误差小。

(3) 在量级比较上，两模型水平方向误差均高于垂直方向，这主要是因为不同测深点平面位置叠加了±0.1 m的GNSS定位误差。

(4) 改进模型变化幅度比Rob Hare模型快是因为改进模型在水平方向上考虑了升沉误差和吃水误差对声线跟踪起始位置的影响，导致水平方向误差比Rob Hare模型大。

(5) 随机选取第60ping共512个波束对，其误差进行分解如图6(a)、(b)所示。在水平方向上图6(a)随着波束入射角增加，由吃水改正误差引起的误差在改进模型中逐渐增大，是改进模型总误差边缘大于Rob Hare模型的主因。在中央波束附近总水平误差突起是由于振幅检测测角误差比相位检测方式误差贡献量大造成；在垂直方向上图6(b)，振幅检测导致的测距误差小于其代表性误差贡献量，是改进模型中央波束总误差小于Rob Hare模型的主因。改进模型边缘波束总误差逐步大于Rob Hare模型是由于随着波束入射角增加，相位检测的边缘波束采样数相比中央波束减少和改进模型使用常梯度声线跟踪，边缘波束比Rob Hare模型跟踪距离长，误差累积大共同造成的。

以上对比分析表明，改进模型较RobHare模型在水平和垂直航迹方向根据各自波束特点考虑了更多的误差因素，更精细地刻画了单个波束的误差分布规律。

3.3 与交叉点不符值中误差比对分析

在多波束测量误差分析与评估中，通过模型计算得出的中误差为先验式误差，即得到该水深点存在的理论中误差值，而交叉点不符值[18]评估为后验式误差[19]，即可获得该点实际测得中误差值，两种方式都是衡量数据的偶然误差分布规律[20]，其中误差的置信度相同，在统计上应呈现一定程度的相关性。因此为了说明改正模型能客观评价数据的误差分布，将其与通过交叉点不符值求得的中误差进行对比分析。

(1) 交叉点不符值中误差计算。1、2号测线交叉点共计152 201个，以每一个交叉点为圆心，搜索一定半径范围内的交叉点不符值(交叉点个数一般不小于50)，利用圆内交叉点不符值计算得到该交叉点的中误差。计算得到的区域交叉点不符值中误差如图7所示。

(2) 改进模型计算交叉点中误差。利用本文提出的改进模型和Rob Hare模型分别计算1、2号测线测深点水平和垂直中误差，为便于水深误差计算，类比于合成不确定度[21]，应用误差传播率将水平中误差转化为垂直中误差，即将水平中误差与海底地形斜率建立联系，斜率越大则水深定位点误差受水平方向中误差影响越大。若计算点周围海底地形的平均斜率为s，则总的测深点水深误差的计算公式为

(22)

绘制改进模型和Rob Hare模型计算交叉点中误差等值线图，如图7所示。

(3) 对比分析。由图7(a)、(b)、(c)对比分析可以发现：①通过式(22)计算的交叉点中误差与两误差模型计算量级相当，整体分布规律基本相似，呈现四周边缘大、中间小、四角略大的整体变化趋势，原因在于中间为两条测线中央波束相交区域，四角为边缘波束相交区域(参见图4中测线分布)，中央波束数据精度一般高于边缘波束，导致误差整体呈现一种凹球面分布状态，符合误差分布规律；②交叉点中误差局部分布规律相似，如图7和图4中标出的黑色圆形区域，原因在于交叉点误差受海底地形倾角影响，海底地形变化越剧烈(图4)，局部交叉点中误差越大；③图7(a)、(b)中红色圆形区域表示改进模型和真实数据计算交叉点不符值相似区域，而在图7(c)中不存在类似相似，其原因是图中红色圆形区域为改进模型相比Rob Hare模型改进较大区域(图5、图6)。以上分析表明，改进模型能客观评价多波束测量数据质量，更精细地刻画了单个波束的误差分布规律。

图5 1号测线改进模型和Rob Hare模型垂直、水平方向中误差Fig.5 The vertical and horizontal errors of the improved model of survey line 1 and Rob Hare model

图6 第60ping波束改进模型主要误差分解Fig.6 The 60th ping beam main errors decomposition diagram

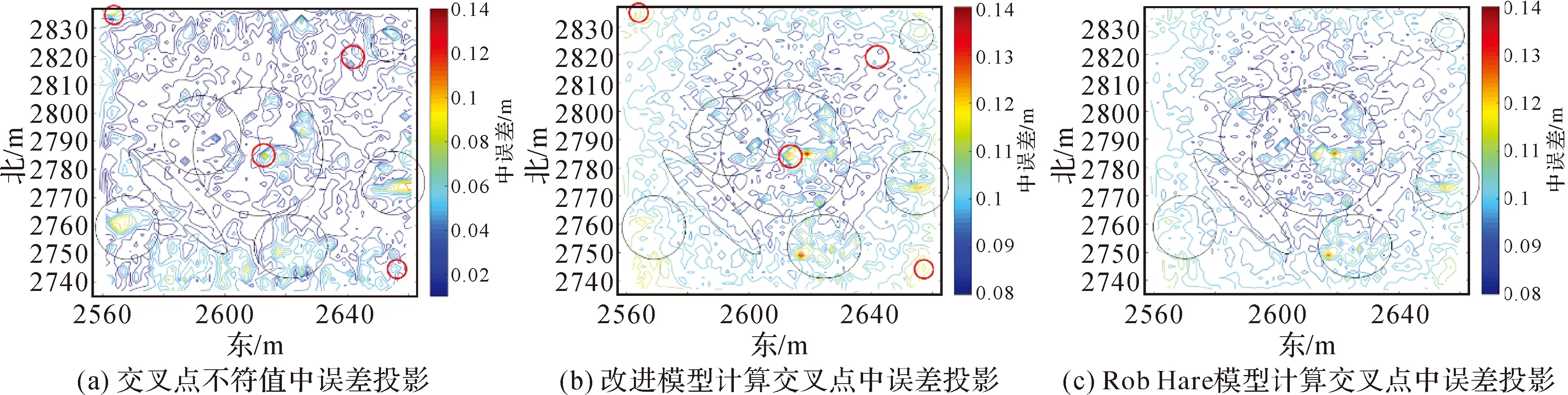
图7 模型计算误差与交叉点不符值中误差比对Fig.7 Comparison of error between model calculation error and cross point discrepancy

3.4 基于CUBE曲面比对验证

本文基于CUBE模型生成曲面来对本文构建的改进模型和Rob Hare模型进行分析比对。

为了进一步定量验证改进模型，本文在1、2号测线重叠区域建立比对区域，以不同格网点间隔(node spacing)为变量，取格网点最小捕捉半径(capture distance min)5、最小捕捉半径系数(capture distance scale)0.5、水平不确定度传播比例系数(hes)2.95和估计偏移值(estioff)4，4个核心参数不变，其余判断阈值为默认值[22]，分别建立1、2号测线交叉区域CUBE曲面，计算重叠CUBE曲面交叉点不符值均值和中误差，如图8所示。

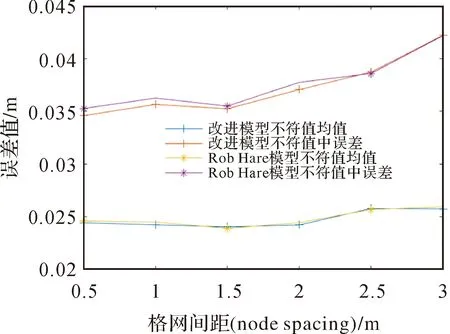
图8 改进模型与Rob Hare模型CUBE曲面比对结果Fig.8 CUBE surface comparison results between the improved model and Rob Hare model

由图8可知，随着格网间距的缩小，改进模型与Rob Hare模型不符值中误差呈现减小趋势，说明两模型均能提高数据质量，其中改进模型不符值中误差下降幅度较Rob Hare模型更快,在格网间距为0.5 m时减弱了约2%中误差，以上表明，改进模型对数据中偶然误差的刻画更为详尽且符合真实情况，验证了改进模型误差组成更完善的优势。

4 结语

本文建立的多波束测深系统误差改进模型，基于精确波束入射角度推导，以常梯度声线跟踪模型为基础，结合Rob Hare经典误差分类，构建了回波检测方式、吃水改正和升沉改正误差综合影响下的多波束测深误差改进模型。实测数据计算结果表明，改进模型相较Rob Hare误差模型考虑的误差因素更多，更能精细地刻画测点误差分布规律，误差构成更加完善，更能反映数据中存在的随机误差分布。通过与交叉点误差对比分析，主检CUBE曲面差值对比等方式，验证了本文构建误差模型的正确性和有效性。改进模型有助于发现问题和剥离误差源，更准确地分析各误差源导致的误差量级大小，研究成果为数据质量控制、数据检核提供理论依据和技术支撑。

本文选取的实例使用Reson T50-P浅水多波束测深系统精度较高，作业规范，各误差源量级较小，导致部分误差源量级较小，对于其他不同多波束测深系统还应具体区分其量级大小。