页岩油藏多段水平井压后关井阶段压力扩散数学模型研究
2022-05-31赵振峰刘汉斌杜现飞徐创朝赵号朋
赵振峰,刘汉斌,杜现飞,徐创朝,赵号朋
(1.中国石油长庆油田分公司油气工艺研究院,低渗透油气田勘探开发国家实验室,陕西西安 710018;2.中国地质大学(北京),非常规天然气地质评价与开发工程北京市重点实验室,北京 100083)
0 引言
水平井压裂技术已成为开发页岩油储层不可或缺的工艺,往往起到关键的作用(杜金虎等,2014;林旺等,2018;徐永强等,2019)。鄂尔多斯盆地具有丰富的页岩油资源,勘探开发潜力巨大,加强鄂尔多斯盆地页岩油研究对中国页岩油资源的勘探开发具有重要意义(严锐涛等,2016;梁晓伟等,2017;张娟等,2019;杨兆中等,2019)。现场压裂施工和关井过程中,关井时间长短直接影响工作制度和产量,因此分析压后关井压力扩散随关井时间的变化至关重要。
水平井压后关井时间不同造成压力分布差异,影响压裂液滤失面积,进而影响水平井产量。延长关井时间,压裂液滤失范围广,通过致密储层发生渗吸作用可以提高一定的产量,但关井时间太长造成产量增长慢,反而得不偿失。关于页岩油藏的产量与渗吸、关井时间的关系,国内外学者都做了大量渗吸实验和数值模拟研究(屈雪峰等,2018;王冲等,2018;王秀宇等,2019)。Bertoncello et al.(2014)研究了非常规气藏返排制度和早期产量:关井有利于压裂液进入基质孔隙发生渗吸作用,但关井时间过长又会影响压后产能,需要综合考虑关井时间。Wang et al.(2015)对致密储层返排数值模拟的研究中,认为压后关井期间,基质的渗吸作用能较好地提高单井产量,但其仅表现在初期。Fakcharoenphol et al.(2016)为研究关井时间对产量影响,采用数值模拟研究,认识到延长关井时间可有效提高气井早期产量,其原因为毛管力等影响下的渗吸效应。李帅等(2016)考虑了压后关井的压裂液渗吸问题,并考虑渗吸作用等修正了相渗曲线,运用修正数据进行数值模拟研究,该研究为计算开采初期含水率变化提供一种方法。
水平井压后压力扩散表征和产量计算一直以来都是研究的重点,学者们通过建立模型、数值模拟和参数优化等手段和方法来计算产量、评价压裂效果(姜瑞忠等,2015;苏皓等,2018;徐加祥等,2019)。李勇明等(2012)考虑水平井多段裂缝和单条水力裂缝压力递减方式的不同,制定了多段水平井压力递减分析方法,可以进行压裂参数解释。闵春佳等(2015)通过数值模拟研究压裂参数和水平井水平段长度对单井产能的影响,给出了优选裂缝间距、裂缝长度和导流系数,并未提及关井时间对产能的影响。蒋廷学等(2018)介绍了一些水平井体积压裂过程的关键技术,包括压裂和返排过程中的参数优化方法,结合技术研究与现场应用提出来改善体积压裂效果的一些建议,侧重点在压裂和返排对产能的影响。姜瑞忠等(2019)认为不能忽略页岩油储层基岩中的非稳态窜流,建立了包括压裂改造区非稳态窜流的五线性流数学模型,得到压力动态曲线。王欢等(2020)建立压裂水平井复合试井模型,分为压裂改造区和非改造区两部分研究,得到井底压力特征曲线,依据渗流特征进行分段并进行敏感性参数分析。学者们研究关井后渗透率、水平井长度等对压力和产量的计算,甚至裂缝导流能力和压力敏感性对产量的影响,但对确定关井时间研究较少,对现场来说一个确定的参考关井时间很重要,且计算关井压力变化需考虑压裂过程,因为压裂施工时会影响关井阶段初始压力,导致最佳关井时间不同。
由于关井阶段初始压力分布不再是原始地层压力,为分析压后关井压力扩散随关井时间的变化,本文首先建立压裂液注入模型,计算压裂后的地层压力分布;然后建立关井阶段压裂液滤失模型,考虑渗吸作用置换量,此时模型内部网格初始压力则应用注入完成后地层压力分布数据,计算关井结束后地层压力变化;根据页岩油藏多段水平井压后关井阶段压力扩散和压裂液波及范围受关井时间影响与变化情况,初步确定最佳关井时间,充分发挥压后关井渗吸作用,对返排制度优化及提高单井产量具有指导意义。
1 压裂液注入模型
1.1 模型假设
压裂施工时压裂液在高压下沿裂缝不断注入到地层中,裂缝内高压逐渐扩散,使近井地带的原始地层压力升高,形成压力梯度进一步扩散。为了研究地层压力变化,考虑压裂液井筒内流动和压裂液在地层中二维滤失,根据岩石力学及流体力学相关理论,构建压裂液注入物质平衡关系,基于以下假设条件建立压裂液注入模型:
(1)假设压裂施工时压裂液排量为3 m3/min,每10 min裂缝向前扩展一个网格;
(2)建立四分之一油藏网格模型,研究压裂液二维滤失,在裂缝方向(X方向)和垂直裂缝方向(Y方向)根据压力分布特点确定模型网格长度:
X方向:压裂单位时间内扩展裂缝长度逐渐减小,故确定X方向网格长度时采用递减数列;
Y方向:压裂液主要从裂缝中沿Y方向滤失至地层中,靠近裂缝的地层附近压力梯度大,采用较密网格,离裂缝越远则采用较疏的网格;
(3)靠近裂缝的地层网格(即y=1的网格)设置为裂缝压力,且施工过程中裂缝压力保持恒定;
(4)四分之一油藏模型中与其余部分油藏相交边界为封闭边界条件,X方向和Y方向远端外边界条件为地层原始压力。
在压裂液注入阶段,依据物质平衡可知注入地层的压裂液一部分保留在压裂的裂缝体积内,另外一部分滤失进入裂缝周围地层,压裂液的注入量等于压裂液的滤失量加上裂缝的体积变化量,建立注入压裂液二维滤失模型并计算滤失量,且由裂缝体积模型计算裂缝的体积变化量。
1.2 注入压裂液二维滤失模型
依据连续性方程和达西定律,推导出压裂液发生渗流时微分方程如下:
(1)
考虑四分之一油藏,则模型边界条件为:
封闭外边界:
(2)
定压外边界:
P|y=Ly=Pi;P|x=Lx=Pi
(3)
内边界条件:
P|x≤lf,y=0=Pf
(4)
模型初始条件:
P|t=0=Pi
(5)
求解渗流微分方程及附加条件组成的五对角方程组,采用强隐式方法得出各网格点的压力。根据滤失速度:
(6)
根据靠近裂缝的网格点的压力与裂缝压力的压差,则计算单位时间压裂液滤失量为:
(7)
总滤失量:
(8)
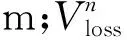
压力扩散模型假设在每一个时间步长内扩展出一段裂缝,计算此时间步内的压力场分布并赋值给下一时间步。建立模型时,首先根据裂缝长度和段间距等建立网格系统,裂缝方向网格长度逐渐减小,垂直裂缝方向根据距离裂缝远近选择网格长度;每个时间步长内计算时,扩展的裂缝网格设置为裂缝压力,利用二维滤失模型计算各网格点压力。压裂过程裂缝逐步扩展的压力图如图1所示,选取展示裂缝在扩展至第2、4、8、12段(即t=20、40、80、120 min)时的四分之一裂缝和水平井周围地层压力分布,压力充填裂缝的同时逐渐向地层外层扩散。
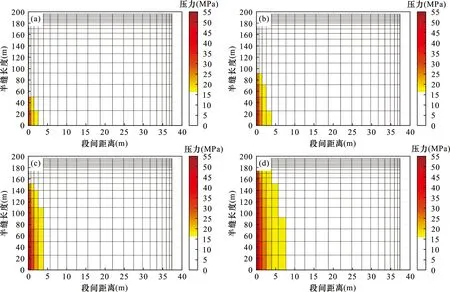
图1 裂缝扩展20 min(a)、40 min(b)、80 min(c)、120 min(d)时裂缝周围四分之一地层压力分布
Fig.1 Pressure distribution of a quarter of formation around the fracture when fracture propagating at time 20 min(a),40 min(b),80 min(c)and 120 min(d),resepectively
在二维滤失模型中,随着压裂施工的进行,靠近裂缝的地层网格的压力也逐渐增长为裂缝压力。在每个时间步长内,根据注入到地层中的压裂液物质平衡,建立等式关系,即压裂液注入体积量等于压裂液滤失量加上裂缝的体积变化量,以此进行迭代计算,最终得到压裂施工结束后的地层压力分布和裂缝的滤失量。
2 压后关井模型
不同于压裂液注入过程,压后关井无能量注入,此时物质平衡方程:裂缝体积变化量=压裂液滤失量,且此时压裂结束时地层压力分布成为关井初始时刻压力分布,所以模型计算时把注入模型最终得到的压力数据作为关井初始压力,在注入模型基础上建立关井阶段压力扩散模型。
2.1 模型假设
(1)考虑压裂液从裂缝向地层中流动,同时考虑滤失范围内的渗吸过程,建立压裂液二维滤失模型;
(2)模型内部网格初始压力则应用注入完成后地层压力分布数据。
2.2 压后关井二维滤失模型
依据连续性方程和达西定律,地层中压裂液发生渗流时,微分控制方程如下:
(9)
关井阶段二维滤失模型,考虑通过渗吸的流体交换过程,从小孔隙中渗吸出的油为流入量,从大孔隙进入到小孔隙中的压裂液为流出量,渗吸量受到孔隙两侧压力及流体、岩石性质的影响,根据计秉玉等(2002)和王希刚等(2013)的研究,综合对渗吸过程进行数学模型和模拟的分析,本文计算渗吸量表示为:
(10)
式中:α为表征裂缝发育状况的形状因子,1/m2;km为基质有效渗透率,m2;Pm为基质压力大小,Pa;Pf为裂缝中压力大小,Pa。
因此模型中二维单相渗流控制方程表示为:
(11)
与压裂施工过程中压力分布数学模型的初始条件不同,此时井底压力分布经压裂发生了变化,初始条件应为压裂后压力分布数据,即:
P|t=0=P压后
(12)
同样对控制方程进行差分和简化,得:
(13)
合并相同未知量得:
(14)
其中:
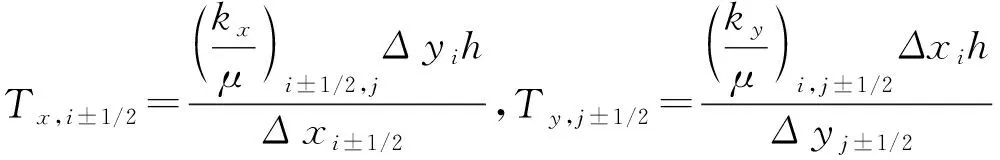
2.3 裂缝体积模型
压裂技术的发展引起学者们对压裂裂缝形态的研究,形成了多种水力压裂模型(姚飞和王晓泉,2000;杨丽娜等,2002;崔光锋等,2003;刘建军等,2003;金衍等,2016)。三维的裂缝形态描述十分复杂,各种模型的简化假设多基于流体在裂缝内的流动状态和裂缝的长宽高变化。本文采用拟三维(P3D)模型计算裂缝体积,拟三维模型相较二维模型更加准确且避免了真三维模型的复杂计算。假设地层为线弹性体,层间无滑动,模型考虑裂缝高度的延伸变化(李静嘉等,2012),假定在闭合期间裂缝长度和高度不变,而且裂缝高度呈椭圆形分布。
根据England和Green公式,井底的裂缝宽度横截面的最大缝宽为(Palmer and Carroll,1983):
(15)
而在停泵时刻,裂缝的体积表示为:
(16)
式中:
(17)
(18)
关井裂缝不断闭合期间,由于缝长和缝高不变,仅有缝宽变化。设刚停泵时井口压力为Pf(t0),停泵后某时刻裂缝体积的变化量为:
(19)
由此给定某一时刻的井底压力就可计算该时间段裂缝体积的变化量表示为:
(20)
上式中:Pf(t)为t时刻井底压力,Pa;Pf(t0)为停泵时刻的井底压力,Pa;γ为地层岩石泊松比;E为地层岩石弹性模量,Pa;Hp为压裂层厚度,m;Hw为井底裂缝高度,m;s1为压裂层水平最小主应力,Pa。
在每个时间步长内基于裂缝与网格压差计算压裂液滤失量,用裂缝体积模型计算裂缝体积变化量,根据物质平衡压裂液滤失量等于裂缝的体积变化量可以求出下一时刻压力,进而得到压后关井地层压力分布。
2.4 模型计算流程
压裂与关井是连续的操作过程,井底压力变化也应考虑两部分的连接。多段水平井压后关井最佳时间的确定,需建立压裂液注入模型和压后关井滤失模型,建立压力扩散模型可以计算压裂结束时刻井底附近地层压力分布,应将压力数据赋值给压后关井初始时刻并且进一步代入压后关井模型计算,分析地层压力变化可以为压后并井时间提供理论支持。图2所示水平井压裂结束地层压力分布图,压裂后裂缝周围地层压力增加,缝间未波及部分仍为原始地层压力,关井阶段的压力场分布在此基础上继续扩散,当压力扩散达到稳定时,优选压后关井时间可以增加波及体积,进而增加油气产量。
具体计算流程如下:
(1)在数据收集的基础上,首先建立压裂液注入模型,确定生产制度和网格大小;
(2)利用物质平衡方程,压裂液注入量等于裂缝体积增加量加上裂缝向周围地层的滤失量,计算压裂后井底压力变化;
(3)建立关井阶段压裂液滤失模型,考虑渗吸作用置换量,初始压力则应用注入完成后地层压力分布,计算关井时间内地层压力变化;
(4)根据两部分建立的综合模型,计算压裂液波及体积随关井时间变化,以确定最佳关井时间,最后对关井后油藏压力影响因素进行分析。
图2 水平井压裂结束地层压力分布示意图
3 实例验证
鄂尔多斯盆地陇东地区页岩油资源丰富,是近年来石油勘探的新层位,具有很大的勘探开发潜力。陇东页岩油藏分布主要受岩性和物性控制,原油的原始气油比和饱和压力较高,综合认为油藏天然能量以弹性溶解气驱为主。随着油藏深度的增加,地层压力增大,油层温度升高。油藏地层温度为58.9 ℃左右,地温梯度2.8 ℃/100 m,原始地层压力15.8 MPa,压力系数为0.83。选取现场W-1和W-2两口井数据进行模型计算,基本参数见表1。
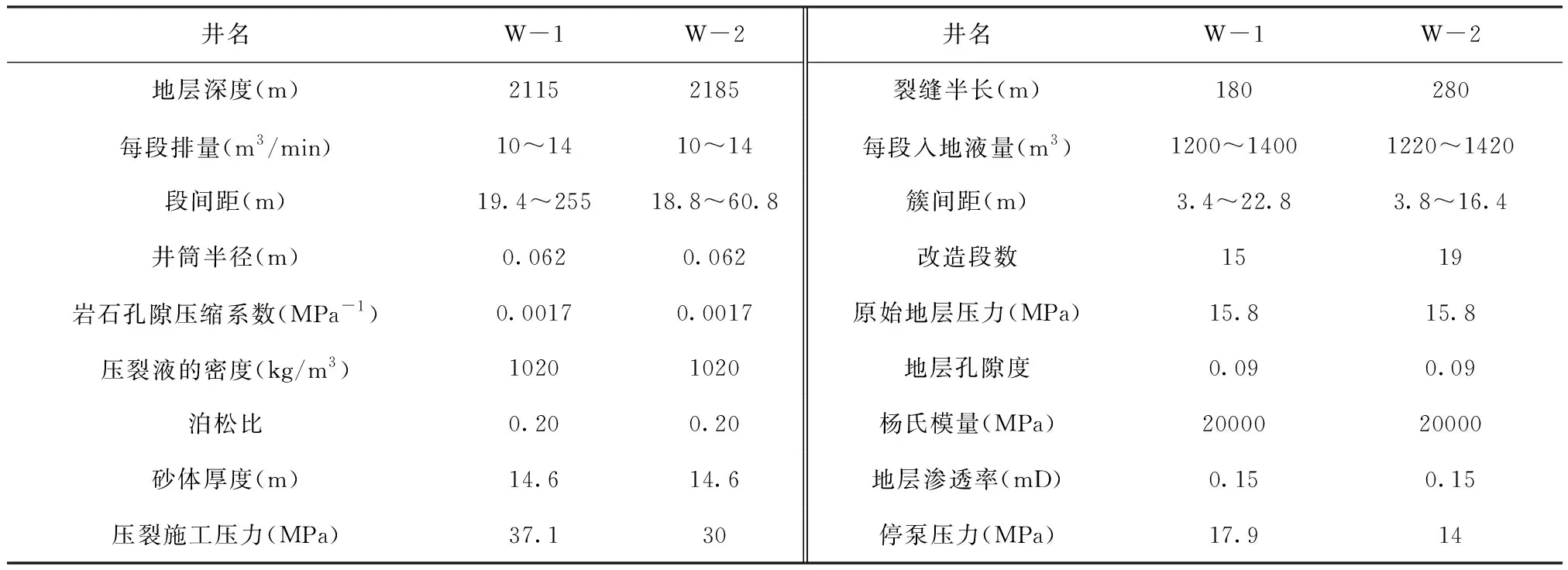
表1 两口实例井基本参数表
3.1 关井过程压力变化
压裂过程中,随着裂缝不断向前扩展,沿裂缝方向和裂缝两侧压力逐渐向外传播,压裂后簇间压力变化大,在短时间内压力较两侧高,某段压裂完成后压力分布如图3所示。可以看出在一段五簇同时压裂情况下,裂缝内的压力都等于压裂压力,压力高表示为红色部分,两侧临近区域和簇之间压力均有所上升,且能看到压力传播覆盖簇之间区域,两侧压力分布对称。
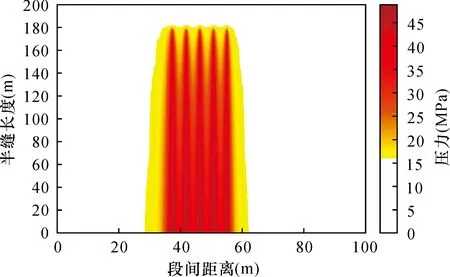
图3 压裂完成后某段压力分布
关井阶段初始压力即为注入阶段结束时压力分布,经过初期压力缓缓扩散(图4),末期压力扩散范围扩大至段间较远距离,影响下一段压裂初始压力分布(图5)。
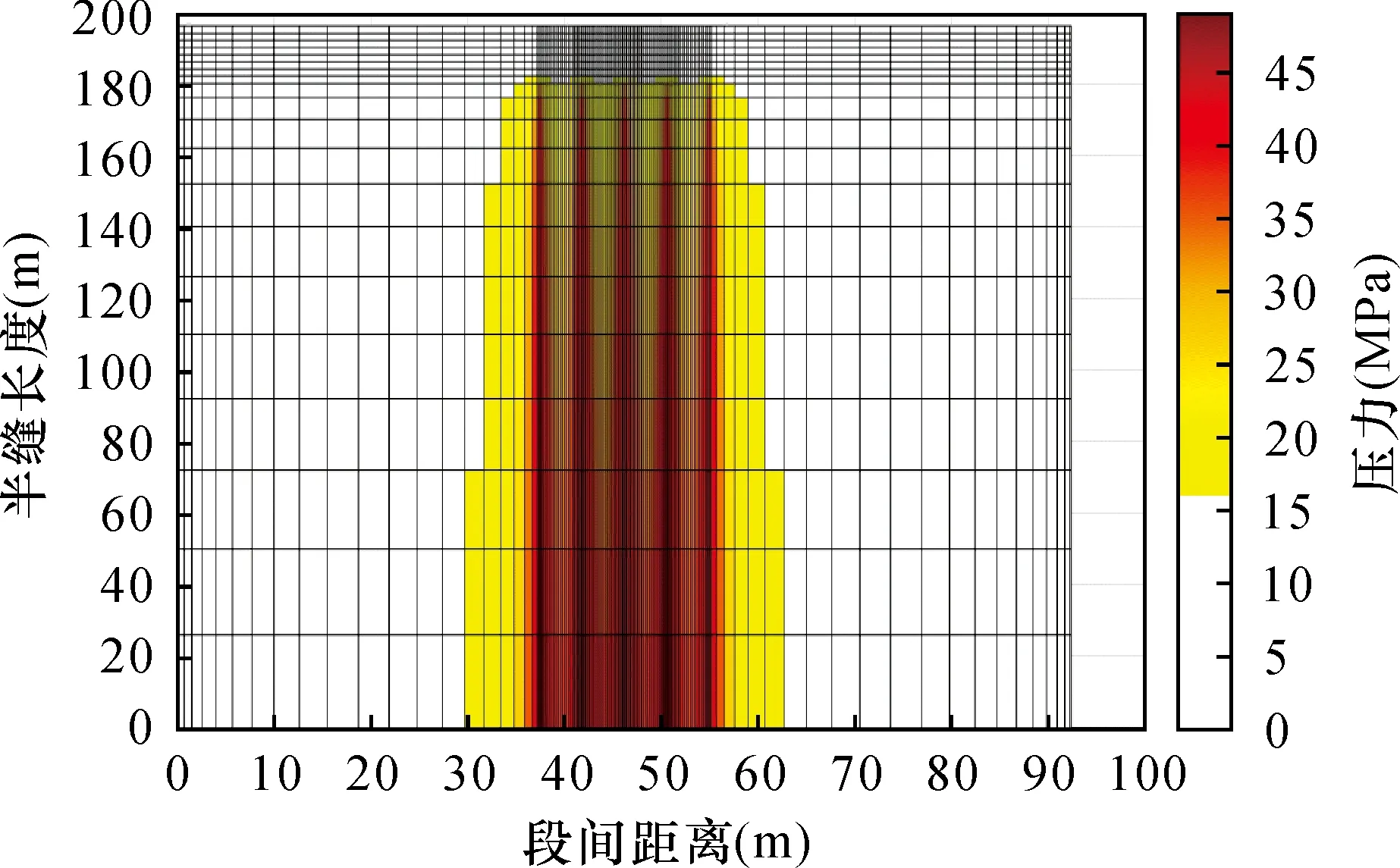
图4 关井过程初期裂缝周围压力分布
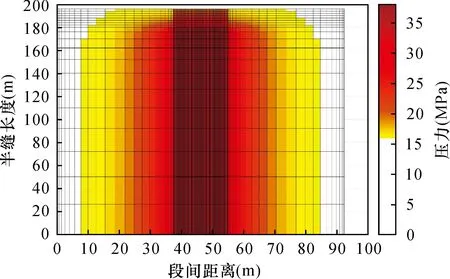
图5 关井过程末期裂缝周围压力分布
关井阶段计算时,压力变化缓慢,段与段间压力向中间逐步扩散,簇与簇间压力缓慢升高。此过程伴随着裂缝中的压裂液滤失到地层中,使得累计滤失量增加,由于簇间距比段间距离小,压裂液较快地充满簇之间区域,进而发生渗吸作用。
3.2 关井阶段压降曲线模拟与预测
关井阶段模型中将注入阶段得到的裂缝周围压力分布作为关井初始阶段压力分布,计算压力变化情况,依据平衡关系裂缝体积变化量等于滤失量,计算下一时刻的裂缝压力,最终表示出关井阶段的压降曲线。将关井井底压力绘制实测井底压降曲线,将模型计算统计结果与实际统计压降曲线对比,如图6和图7所示,实际压降数据统计时间较短,与模型计算压力降落曲线早期段拟合效果较好,井底压力会随着关井时继续降低。
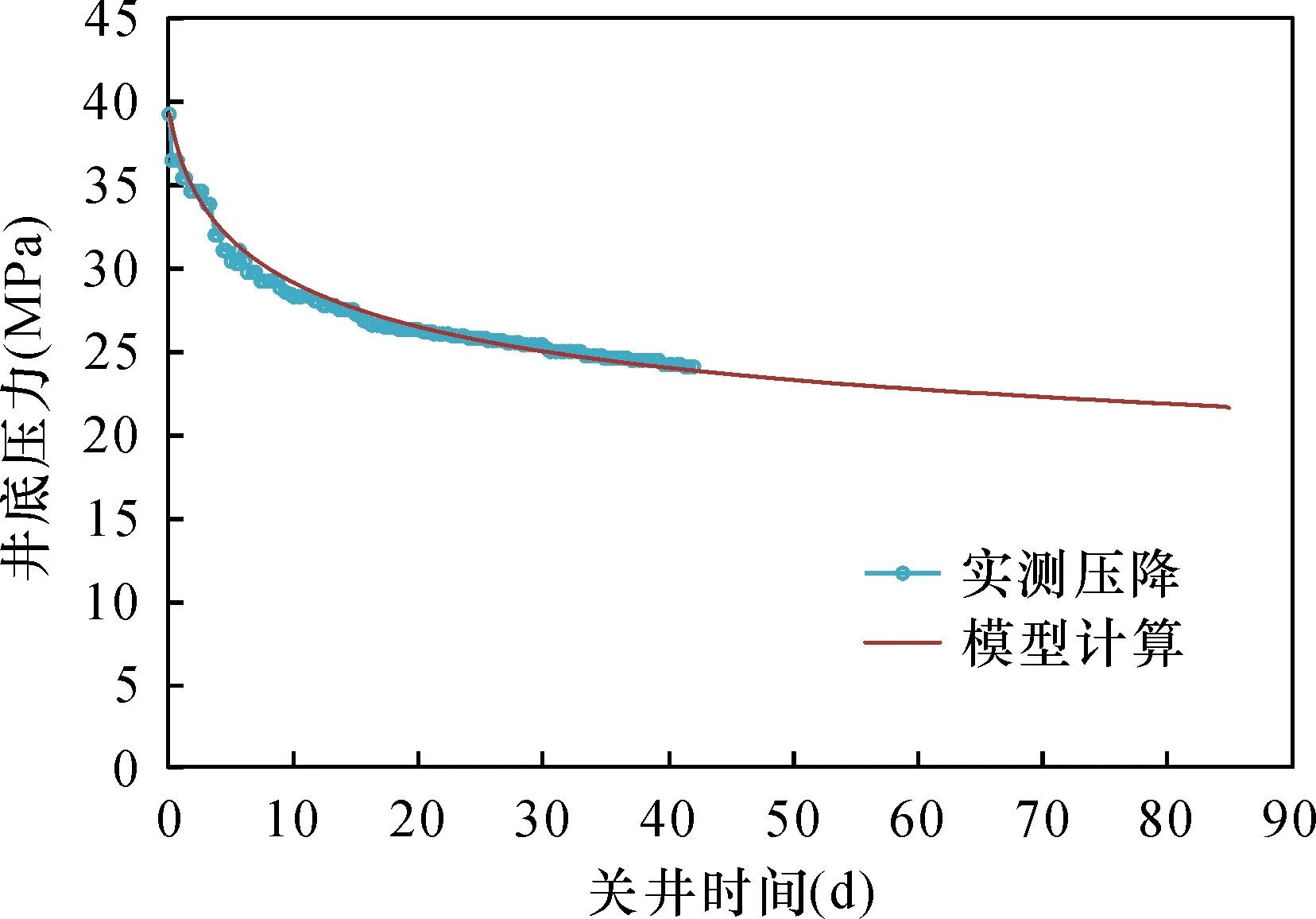
图6 W-1关井阶段压力降落曲线对比
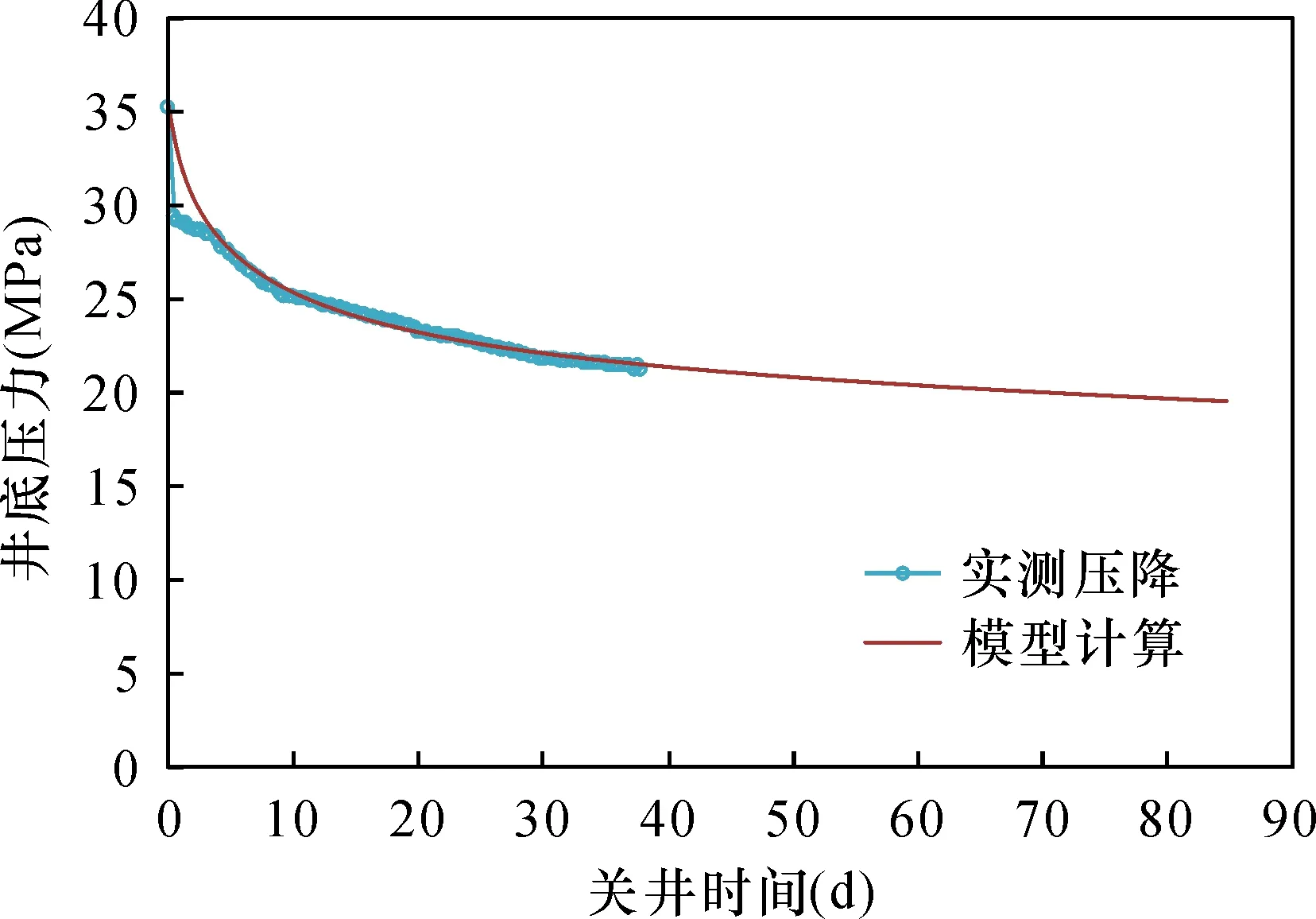
图7 W-2关井阶段压力降落曲线对比
3.3 压裂液波及体积变化
依据模型计算井底地层压力和关井过程中因滤失液的滤失形成的压裂液波及体积,如图8和图9。波及体积随关井时间不断扩大,与井底压力的变化时间有相似之处,初期波及体积增长较快且逐渐趋于平缓,可以看出W-1和W-2分别在关井时间约58天和61天压裂液波及体积增速变缓,据此判断压后最佳关井时间。
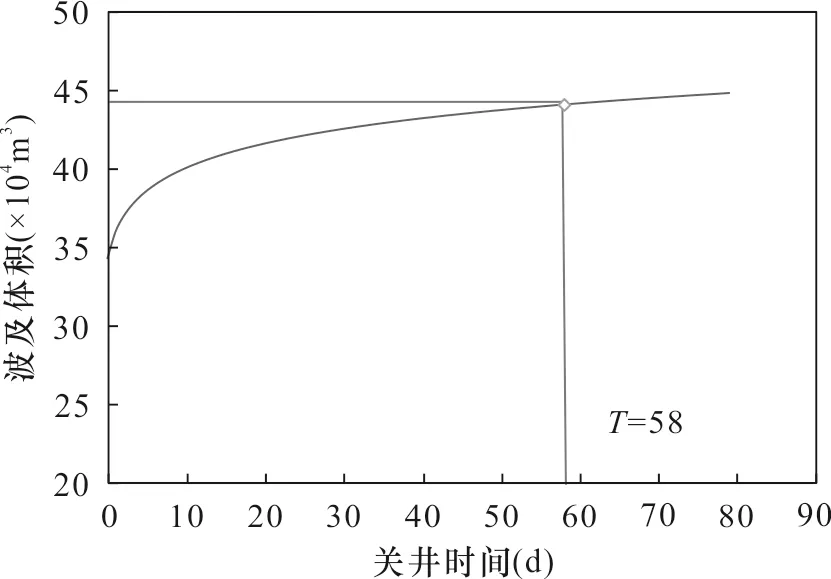
图8 W-1关井阶段压裂液波及体积随时间变化
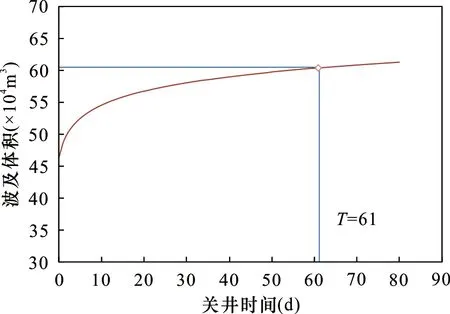
图9 W-2关井阶段压裂液波及体积随时间变化
4 影响因素分析
关井压后压力分布直接反映了压裂与关井的施工效果,为后续返排及采用合理放喷等生产制度提供理论依据,进而影响最终产量。根据前述建立考虑渗吸的关井后二维滤失模型,本文进行了孔隙度渗透率等因素对关井压后压力分布的影响结果,为页岩油藏水平井压裂及关井后压力分析提供参考。
4.1 孔隙度
孔隙度对压裂过程和关井过程都有影响,孔隙度大的致密储层相比基质含有更多的流体,影响压力的传播和扩散。在模型中运用控制变量法,通过对一口井设置不同的孔隙度计算压后关井时刻井底地层的压力变化(图10),图10开始时刻为压裂结束关井开始,孔隙度大则压裂结束时井底压力较大;随着关井时间井底压力均逐渐减小,孔隙度越大压力减速越缓慢,整个过程孔隙度越大井底压力越大。
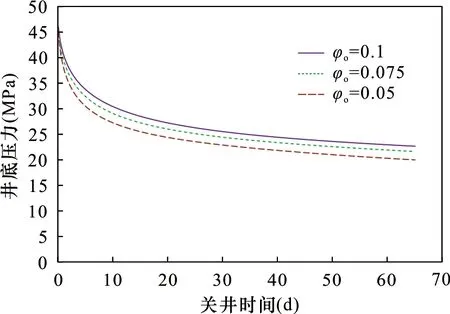
图10 不同孔隙度下井底地层随关井时间的压力变化
4.2 渗透率
研究不同渗透率下关井后地层压力变化,进行模型计算表示出压力随时间变化(图11)。井底压力随着关井时间逐渐减小,储层的渗透率越大,则压裂后井底的压力越小,且在关井阶段井底压力越小,可以认为储层的渗透率越大时,液体在地层中的流动能力越强,压力传播和扩散更容易。
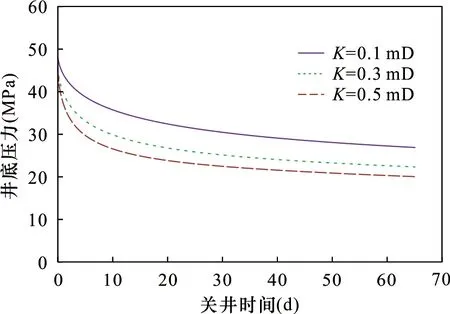
图11 不同渗透率下井底地层随关井时间的压力变化
4.3 注入时间
压裂阶段注入速度和注入压裂液量会影响压裂效果,导致压裂后井底压力分布不同。在模型计算时,考虑注入速度为3 m3/min注入压裂液,计算不同注入时间100 min、150 min、200 min时由于注入压裂液量差异引起的地层压力变化(图12),图中关井初始时刻不同注入液量导致压裂后压力不同,注入量越大,井底能量增加并逐渐扩散到周围地层中,考虑每时间步长裂缝稳定后压力变化,注入时间对井底压力的影响反映在图中关井初始时刻压力大小,这也决定了关井阶段井底压力高低。
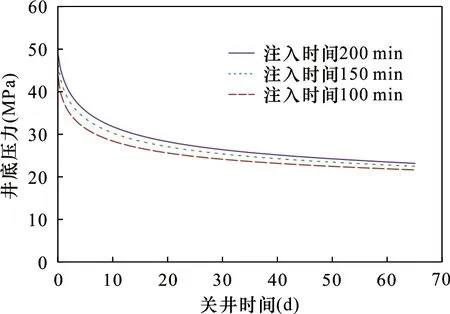
图12 不同压裂液量下井底地层随关井时间的压力变化
5 结论
本文针对页岩油藏多段水平井,建立了压裂施工过程中和压后关井过程中流体压力扩散数学模型,将压裂后地层压力赋值为关井阶段初始压力,对最佳关井时间的确定及井底压力变化的影响因素进行研究,结论如下:
(1)通过考虑页岩油藏渗吸作用置换量,建立二维滤失模型,得到两口井的关井阶段压降曲线井底压力,与实际压力变化拟合较好,证明了考虑渗吸的合理性和模型的准确性。
(2)压后关井井底压力随关井时间增加逐渐降低,前期压力降落快,后逐渐平缓。
(3)计算陇东页岩油藏两口井压裂液波及体积,其随关井时间的增加逐渐增加,增加的幅度会逐渐降低,存在最佳关井时间。
(4)影响关井阶段压力变化的因素中,储层渗透率越小,孔隙度越大,压裂施工时间越长,则关井阶段井底压力越高。