食用葵花籽尺寸分析与均齐性研究
2022-05-31郁志宏敖日格乐张泽鑫杨丽芳张文杰
王 帅, 郁志宏, 敖日格乐, 张泽鑫, 杨丽芳, 张文杰
(内蒙古农业大学 机电工程学院,呼和浩特 010018)
向日葵是我国北方主要栽培的经济作物之一[1],在粮食作物构成和油料作物生产中占有重要地位,分为油用向日葵和食用向日葵,主要用于压榨和食用、饲用。截至2018年底,我国向日葵种植面积高达92.135万hm2,葵花籽产量高达249.42万t[2],主要集中在内蒙古、新疆、吉林以及甘肃等地,2018年内蒙古自治区葵花籽产量占全国产量的60%以上[3]。研究葵花籽的几何特征和均齐性,为向日葵的种植和葵花籽的收获、清选、分级等机械设计及结构优化提供数据参考,同时对分级、选种、定价及离散元理论模型建立有着重要的意义。其中,葵花籽的均齐性是指葵花籽尺寸大小分布的均匀程度,尺寸分布越离散,均齐性越差,越容易分级,反之越困难。
目前,国内学者针对特定农林作物种子几何特征的研究主要涉及花生[4]、玉米[5]、油菜籽[6]、大麦[7]、人参种子[8]、林木种子[9]、莲子[10]、大蒜[11]、大豆[12]等,但关于食用葵花籽几何特征的研究鲜见报道,缺乏对于葵花籽外形尺寸统计分布特性的理论研究。国内外关于种子均齐性的研究也较少,具有代表性的是美国花生性能测试专家组针对花生荚果的尺寸,选择不同形状、尺寸的筛子对花生荚果进行了分级和脱壳。根据脱壳后花生的尺寸特性、质量大小等因素选择不同的筛子进行分级,再根据等级评定销售价格[13]。王京等[4]对花生种子三轴尺寸间的差异性、分布特性及各品种的尺寸均齐性等进行了研究,提出花生的清选和分级方式。徐陶[11]对大蒜种子的外形尺寸及相关性、均齐性等进行了研究,提出了大蒜的分级标准。本文以内蒙古自治区主栽的3个品种食用葵花籽为例,对其三轴尺寸间的分布特性、相关性、差异性以及各品种的尺寸均齐性进行研究,并进行了清选分级试验,为葵花籽清选、分级等机械化生产加工提供理论依据及技术参考,并为建立较精确的葵花籽粒群模型提供必要的数据支撑。
1 材料与方法
1.1 试验材料
内蒙古自治区主栽的3个品种的食用葵花籽1013、SH361和SH363。
1.2 试验方法
1.2.1 葵花籽外形特征测量
每个品种随机选取100粒葵花籽作为样本[14],通过测量、计算获取其主要外形相关尺寸,研究分析葵花籽的外形特征以及主要尺寸间的相关性、差异性。
形状和大小是农作物籽粒的物理性质[15],其尺寸的定义有多种方法,本研究从机械清选、分级、籽粒仿真建模的角度出发,考虑葵花籽的几何形状,测量其3个轴向尺寸,分别为长度(L)、宽度(W)和厚度(T)。其中长度(大径)是种子最大表面的最长尺寸,宽度(中径)是种子最大表面的最短尺寸,厚度(小径)则是种子最小表面的最短尺寸[13]。
1.2.2 葵花籽外形相关尺寸计算
针对葵花籽不规则的形状,为便于描述其大小,定义了其三轴尺寸、直径、算术平均径、几何平均径、球度、体积、表面积和长宽比。使用精度为0.01 mm的数显游标卡尺测量3个品种食用葵花籽的长度、宽度、厚度。
按式(1)计算籽粒的直径(Dr)[4]。
(1)
按式(2)计算籽粒的算术平均径(Dα)[16]。
(2)
按式(3)计算籽粒的几何平均径(Dg)[14, 16]。
(3)
按式(4)计算籽粒的球度(φ)[14, 16]。
(4)
按式(5)计算籽粒的体积(V)[17-18]。
(5)
按式(6)计算籽粒的表面积(S)[17-19]。
(6)
按式(7)计算籽粒的长宽比(Er)[20-21]。
(7)
2 结果与分析
2.1 食用葵花籽尺寸特征分析
2.1.1 三轴尺寸总体特征
对3个品种葵花籽的长度、宽度、厚度及其他外观尺寸特征进行描述性统计分析,得出平均值、最大值、最小值、标准差、变异系数,并根据K-S显著性水平对数据进行正态分布检验,结果如表1所示。
由表1可知,根据平均值比较3种食用葵花籽的尺寸,葵花籽为扁长型种子(长度>宽度>厚度)。在长度、宽度、算术平均径、几何平均径、体积、表面积上,从大到小依次为SH363、SH361、1013;在厚度、直径上,从大到小依次为SH361、SH363、1013。长宽比可衡量籽粒的伸长率,SH363的长宽比最大,平均值为2.60。球度,即颗粒近于球体的程度,各品种葵花籽的球度相近,且球度较低,则籽粒呈长锥形。从标准差上看,葵花籽在长度上的差异要大于其在宽度、厚度上的差异。变异系数的大小反映了样本个体差异的范围,即数据的离散程度[22],各参数的变异系数均小于30%,其中1013籽粒体积的变异系数最大,为27.14%。对葵花籽的各尺寸进行K-S检验,结果表明,每个品种葵花籽的长度、宽度、厚度、直径、体积的显著性指标值均大于0.05,即在5%的显著性水平下近似服从正态分布(3个品种葵花籽三轴尺寸正态分布如图1~图3所示)。因此,在构建离散元葵花籽粒群时可按正态分布生成。根据标准差的适用范围是服从正态分布的数据,对不服从正态分布的部分参数,即K-S显著性水平小于0.05,如1013的球度、SH361的算术平均径和球度等不做标准差统计。

表1 食用葵花籽尺寸物理特性总体特征
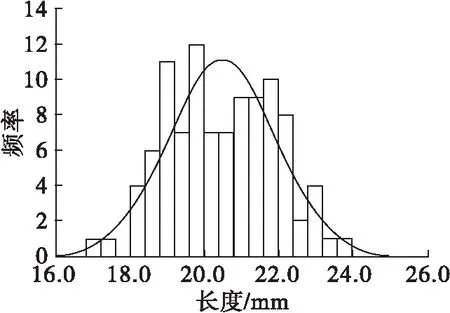

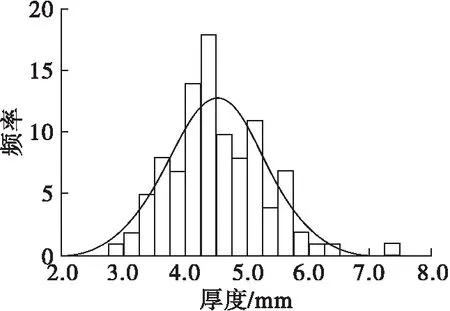
图1 1013葵花籽三轴尺寸正态分布
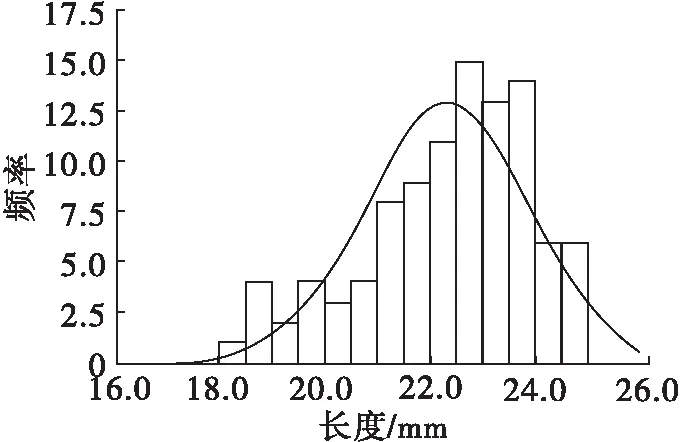
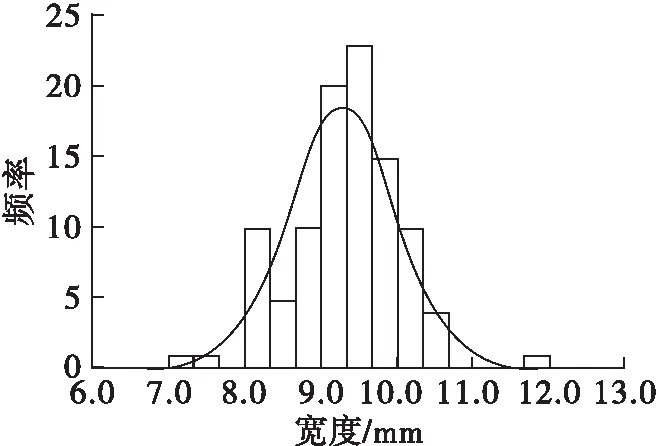
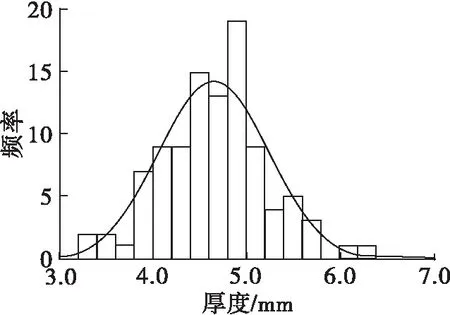
图2 SH361葵花籽三轴尺寸正态分布
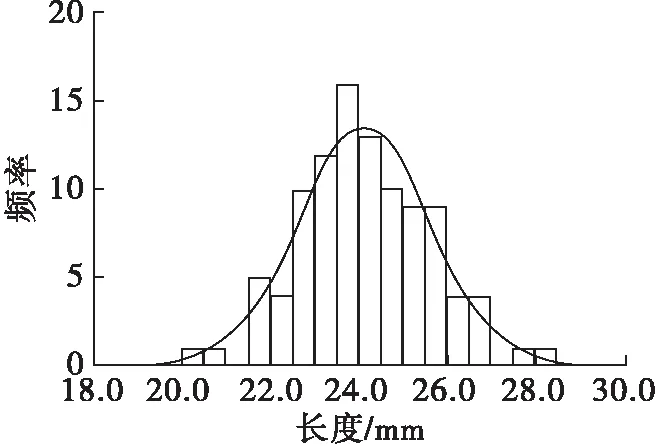
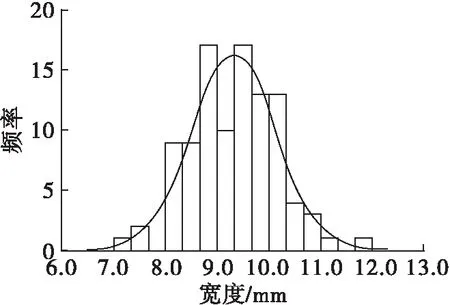

图3 SH363葵花籽三轴尺寸正态分布
2.1.2 三轴尺寸相关性分析
对3个品种食用葵花籽三轴尺寸间的线性相关性进行分析,结果如表2所示。

表2 食用葵花籽三轴尺寸的相关性
由表2可知,3个品种食用葵花籽P值均为0.000,小于0.01,说明各品种食用葵花籽三轴尺寸间具有相关关系。由Pearson相关性值均大于0可知,3个品种食用葵花籽的三轴尺寸间存在线性正相关,各指标不存在负相关的情况。因此,在对葵花籽按大小进行分级时,可选择长、宽、厚中的任一尺寸作为分级标准进行分级。同时,Pearson越接近于1,证明该指标线性相关性越强,因此各品种葵花籽长度与宽度的线性相关性较显著。3个品种食用葵花籽三轴尺寸间关系的散点图见图4~图6。由图4~图6可知,趋势线拟合程度较低,因此在建立颗粒离散元葵花籽模型时,无法建立准确的三轴尺寸关系式,应分别按照三轴尺寸填充颗粒模型,故不同品种葵花籽的离散元仿真分析模型均存在差异。
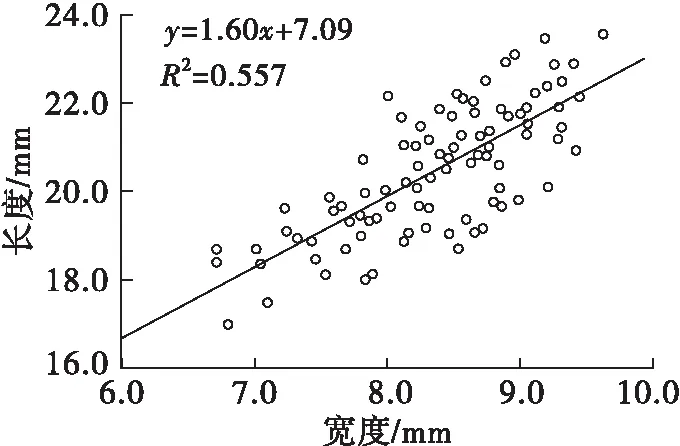
图4 1013葵花籽三轴尺寸间关系的散点图
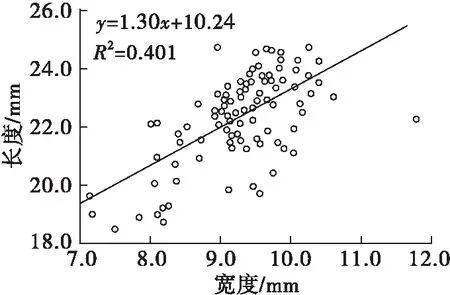
图5 SH361葵花籽三轴尺寸间关系的散点图

图6 SH363葵花籽三轴尺寸间关系的散点图
2.1.3 三轴尺寸差异性分析
将3个品种食用葵花籽分为3组,通过单因素方差分析,比较不同品种葵花籽的长度、宽度、厚度之间是否存在差异性,结果如表3所示。由表3可知,不同品种组间长度和宽度的显著性水平P值为0.000(P<0.01),但组间厚度的P值为0.328(P>0.01),说明不同品种葵花籽的长度、宽度存在极显著性差异,而厚度无明显差异。长度方面,3个品种两两对比P值均为0.000,说明3个品种的长度存在显著性差异;SH361和SH363在宽度上的P值为0.813,表明SH361和SH363在宽度上无显著性差异,而1013与其他两个品种在宽度上存在显著性差异。由以上分析可知,3个品种食用葵花籽在厚度上无显著性差异,且SH361和SH363在宽度也无显著性差异。因此,在清选、分级不同品种的葵花籽时,可通过长度或宽度对葵花籽进行筛选。当以宽度为分级标准时,SH361和SH363可选择同一尺寸规格作为等级分级的标准;但根据长度筛选时,为了结果更加精细准确,需更换筛孔。通常选用窝眼筒进行长度分选或圆孔筛进行宽度分选。
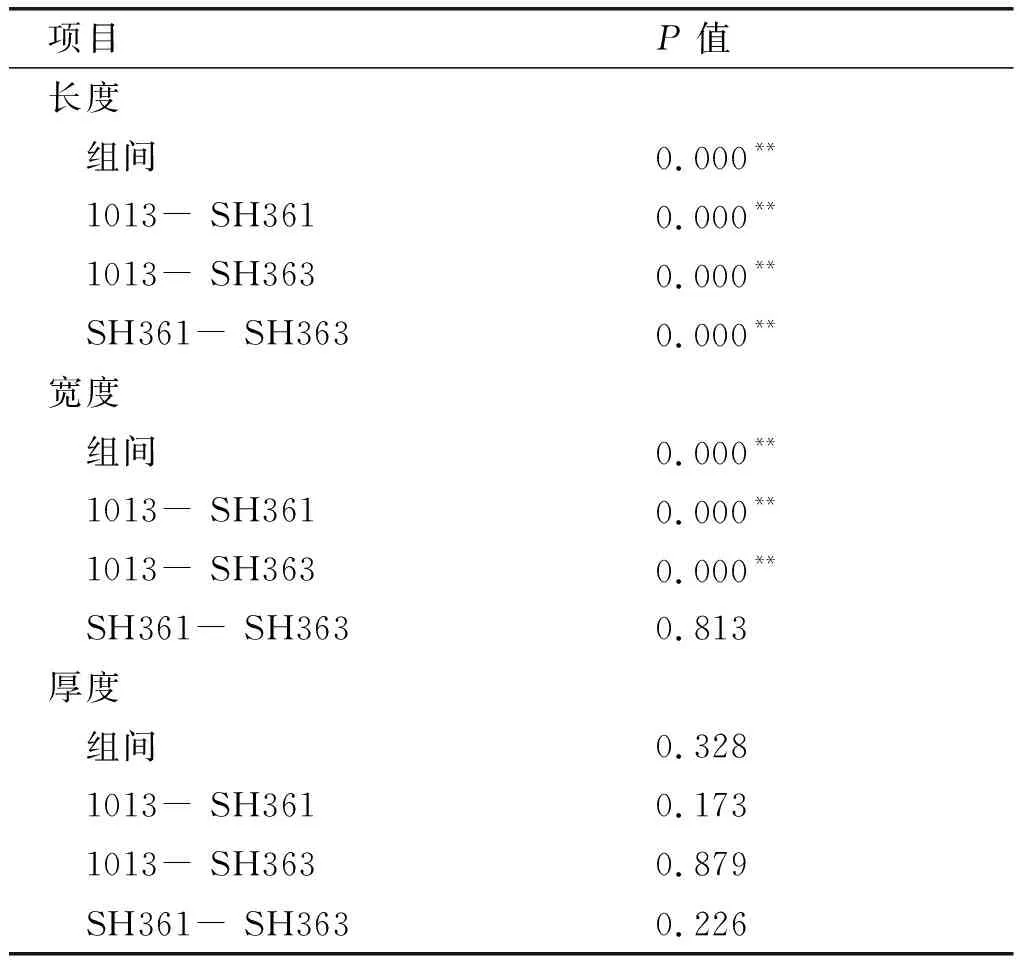
表3 食用葵花籽三轴尺寸的差异显著性
2.2 食用葵花籽均齐性分析
在其他种子机械分级过程中,主要依据种子的直径大小。因此,本研究除三轴尺寸外,引入直径指标分析食用葵花籽的均齐性。累积分布曲线能够直观反映葵花籽尺寸的均匀分布情况。曲线斜率(k)越小,说明种子尺寸分布越分散,均齐性越差,越有利于分级,反之均齐性越好,越不利于分级。在OriginPro 2017中绘制各品种食用葵花籽长度、宽度、厚度和直径的累积频率分布曲线,结果见图7。
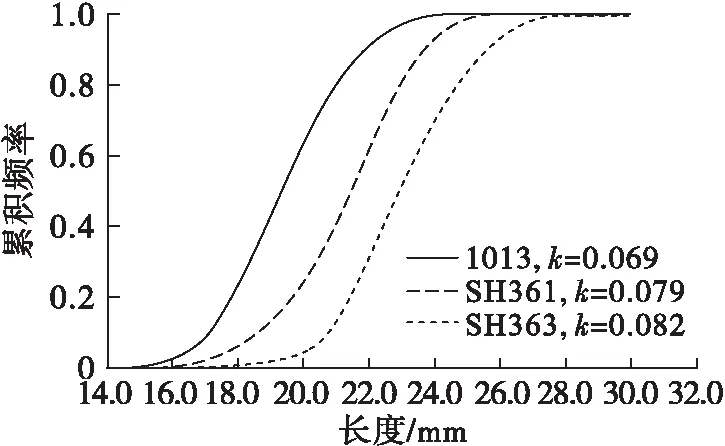
图7 食用葵花籽尺寸累积频率分布曲线
由图7可知,累积分布曲线大体呈线性分布,对各曲线进行线性拟合,根据其斜率(k)的大小确定均齐性。长度上,SH363的尺寸分布最为集中,均齐性最好;宽度上,SH361和SH363的均齐性优于1013;厚度上,1013和SH363的累积频率分布曲线斜率相等,且小于SH361的曲线斜率,说明SH361的厚度尺寸分布更为集中;直径上,SH361和SH363的累积频率分布曲线斜率相等,且大于1013的曲线斜率,说明SH361和SH363的直径尺寸分布最为集中。综合以上情况,不同品种的葵花籽均齐性存在一定差异,其中SH361的均齐性最好,1013的最差。因此,可根据品种以及均齐性来制定相应的分级标准。筛孔的大小要根据葵花籽品种而定,对于均齐性较差的品种,如1013,需要分多级筛选。各品种长度、宽度、厚度、直径4个指标的累积分布曲线斜率从小到大均依次为长度、宽度、厚度、直径。故可得出结论,食用葵花籽按尺寸大小进行分级时,可优先考虑以长度、宽度方向的尺寸作为分级标准。
2.3 食用葵花籽主要尺寸与百粒重的关系
除葵花籽尺寸特征外,葵花籽质量大小也是衡量葵花籽好坏的重要指标。因此,在葵花籽的清选分级及建模过程中还要考虑葵花籽质量大小,本研究选取百粒重作为质量指标。算术平均径与几何平均径能够综合反映种子三轴尺寸大小,因此根据每种葵花籽的几何平均径与算术平均径,分析百粒重与平均径间的关系。3个品种食用葵花籽的算术平均径、几何平均径以及百粒重的平均值如图8所示。
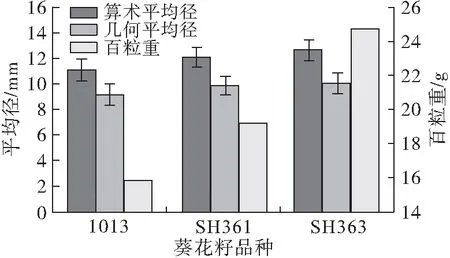
图8 食用葵花籽平均径与百粒重对比
由图8可知,SH363的平均径略大于其他两个品种,1013的平均径最小,葵花籽的百粒重与平均径的变化趋势基本一致,因此可把葵花籽的几何平均径和算术平均径作为葵花籽分级的指标之一。
2.4 食用葵花籽清选分级试验
根据上述分析研究结果,各品种的葵花籽三轴尺寸均服从正态分布,籽粒在长度和宽度上具有差异,厚度无明显差异,且籽粒三轴尺寸具有相关性。因此,为验证研究结果与分级效果之间的量化关系,结合目前葵花籽筛选机实际工况,选用圆孔筛按葵花籽的宽度进行分级试验。每个品种葵花籽各取一份,人工手动去除杂质、干瘪粒等,按GB/T 5491—1985通过分样器法将人工清选后的籽粒分样,使用精度为0.01 g电子天平称取每份籽粒的质量,并计数。由于1013的宽度分布相对分散,均齐性较差,容易分级;SH361和SH363的宽度分布相对较为集中,均齐性较好,分级较困难。因此,试验时1013使用10 mm和8 mm两种规格的圆孔筛,定义孔径10 mm圆孔筛筛板筛上物为大粒级,孔径10 mm圆孔筛筛板筛下物和孔径8 mm圆孔筛筛板筛上物为中粒级,孔径8 mm圆孔筛筛板筛下物为小粒级;SH361和SH363使用10 mm和8.5 mm两种规格的圆孔筛,定义孔径10 mm圆孔筛筛板筛上物为大粒级,孔径10 mm圆孔筛筛板筛下物和孔径8.5 mm圆孔筛筛板筛上物为中粒级,孔径8.5 mm圆孔筛筛板筛下物为小粒级,分级结果如表4所示。由表4可知,各品种葵花籽中粒级占比最大,其中大粒、中粒、小粒占比结果呈正态分布,符合分级要求[23],即大粒级占比不大于10%,中粒级占比大于70%,小粒级占比不大于20%,证明该圆孔筛规格能有效将葵花籽进行分级。

表4 食用葵花籽分级试验结果
3 结 论
(1)1013、SH361和SH363 3个品种食用葵花籽的长度、宽度、厚度、直径、体积均服从正态分布。由三轴尺寸相关性分析可知,三轴尺寸均存在显著线性正相关,但无较准确的关系式,故不同品种葵花籽的离散元仿真分析模型应根据其三轴尺寸分别建立。由三轴尺寸差异性分析可知,葵花籽在长度和宽度上存在显著性差异,厚度无明显差异,故各品种分级时应首选长度或宽度。当以宽度为分级标准时,SH361和SH363可选择同一尺寸规格作为等级分级的标准。
(2)不同品种葵花籽的均齐性存在一定差异,其中SH361的均齐性最好,1013的均齐性最差,1013较易分级。总体上,长度均齐性最差,差异性最显著,可首选长度作为分级的标准。同时,葵花籽的算术平均径、几何平均径与百粒重的变化趋势基本一致,因此可把葵花籽的几何平均径和算术平均径作为葵花籽分级的指标之一。
(3)葵花籽分级试验结果表明,选用圆孔筛按宽度对各品种进行分级时,1013品种选择10 mm和8 mm规格,各级籽粒的占比分别为大粒5.35%、中粒75.75%、小粒18.90%;SH361和SH363品种选择10 mm和8.5 mm规格,各级籽粒的占比分别为大粒9.37%、中粒72.68%、小粒17.95%和大粒8.79%、中粒73.43%、小粒17.78%,均符合分级要求。
