基于模糊逻辑的空冷岛清洗架同步变频控制

李智超，张春光，刘嘉瑞，汪忠伟，宫迎娇

(国机传感科技有限公司，辽宁沈阳 110043)

0 引言

近年来，三相感应电机已在现代工业生产中得到了广泛应用，常被用于驱动水泵、风机和研磨机等，功率从几千瓦到几万千瓦不等[1]。通用变频器作为节约能源的关键设备取得了长足的发展，采用变频器后比直接电网运行省电率达到50% 以上，电机经常运行在低速度时节能效果更显著。由于感应电机低速运行对转矩要求较高，采用通用型变频器控制的电机通常运行在额定功率以下，称为恒转矩运行。随着异步电机无速度传感器控制技术的发展，其低速性能也受到关注。很多学者对此进行了研究，并提出了方法，其中开环 V/F 控制算法易于实现且不依赖电机参数，因而被广泛应用[2]。目前，为了工程上连续加工作业，通常需要各单元组成联合机，各单元分别由1台电动机控制，因此，对单台变频器的控制在许多场合已经不能满足生产要求，必须对多台变频器进行协调控制。文献[3]综述了多电机同步控制技术的主要结构、设计思路、相关应用及其优缺点和改进方案，通过仿真对比了主要同步控制方法的特点，指出交叉耦合控制作为双电机同步系统中常用的控制结构，已经得到了十分完善的发展，同步精度也可以控制在较高的水平。文献[4]指出交叉耦合控制系统是一个多变数耦合控制系统，很难执行交叉耦合控制器上的稳定性分析，且控制器参数选择比较困难。大多使用尝试错误与验证的做法，因此控制器设计困难，且精确度不高，并提出模糊类神经网络控制器设计，以控制双轴线性伺服电机同步运动，从而消除双轴线性伺服电机同步运动的相对速度误差。通过设计2个模糊类神经网络速度控制器，以控制双轴伺服电机同步运动且追随速度命令。结合文献[3-4]的介绍，现今同步策略的主要研究对象为同步电机的转速同步，而在很多联动控制中，异步电机的实时位置同步也至关重要。因此提出一种基于模糊控制器且经优化的交叉耦合结构，实现无编码器异步电机的位置同步，且稳定性好的控制策略是有必要的。

例如空冷岛自动清洗装置中，上、下行电机由各自变频器独立控制，通过倾角传感器实时采样清洗架偏移角，由系统实时计算出频率补偿值，确保不明显减速的条件下，在线校正偏移角。通过引入倾角传感器，形成全闭环系统，从而提高系统稳定性。由于模糊逻辑控制技术对模型不完全确定、复杂的非线性系统具有良好的控制效果[5]，本文主要以清洗架作为研究对象，针对上、下行电机负载时变、倾角传感器及变频控制延时等问题，提出基于模糊逻辑控制的同步变频控制算法，将倾角传感器信号及其变化率作为输入变量，经过模糊语言规则处理，输出控制信号实现清洗架上、下行电机同步运行。对比传统PID控制策略，通过仿真分析，验证系统模型和控制策略的正确性与有效性。

1 调速模型

感应电机 T 型等效电路[6]如图1所示。

图1 感应电机T型等效电路

根据该等效电路可推出电磁转矩为

(1)

式中:Us为输入电压有效值，V；p为电机极对数；s为转差率；L为电感，H；R为电阻，Ω；ω为角速度，rad/s；下标中的s、r、m为定子、转子和磁场量。

由式(1)可得Te-s曲线如图2所示。

图2 感应电机Te-s特性曲线

图2所示输出最大转矩时对应的转差率sm可通过dTe/ds=0求出，sm表示为

(2)

同步转速为ωe时对应的最大转差角频率为

(3)

式中ωe为额定角速度，rad/s。

由图2 可知，sm>0时，感应电机以电动状态运行，当s在[0，sm] 区间时，Te随s的增大而增大，恒转矩负载和恒功率负载在此运行区可稳定运行[7]。

转速开环、恒压频比控制的关键在于协调控制电压和频率，在保证电压频率比Us/ω1不变，即气隙磁通量不变的前提下，通过改变异步电动机的同步转速来实现调速，当转差频率ωs较小时，电磁转矩公式近似为

(4)

式中：Us为定子电压，V；ω1为电源角频率，rad/s；R′r为根据异步电动机的稳态等效电路折算到定子侧的转子每相电阻，Ω。

当电磁转矩一定时，转差频率不变，因此带负载时的转速降不变，可以通过改变定子电压频率来平滑地改变同步转速，从而实现调速。

除定子电压频率外，异步电动机在运行过程中，由于定子旋转磁场转速和转子转速存在转速差，这种不同步导致了电机转差率的存在。异步电动机实际输出转速是电机同步转速和转差率共同作用的结果，由电机机械特性的普遍规律决定。电机实际调速过程，如式(5)所示：

(5)

此时，异步电动机输出机械转矩[8]可以表示为

(6)

式中：CM为与异步电动机结构有关的常数；R2为电机转子回路电阻，Ω；U为电机定子线电压，V；X20为转子转速为0时转子电路的有效感抗，Ω。

为保证电动机变频调速获得良好的转矩特性和调速性能，变频调速最常用的控制方式是恒压频比控制，即式(6)可表示为

(7)

式中k为恒压频比系数，k=U/f，V/Hz。

由式(5)和式(7)可得，同一台电动机工作过程中，f和s是决定电机输出转速和转矩的主要因素。进而，变频异步电动机输出功率可表示为[9-10]

(8)

由式(8)进一步得到，f和s是影响电机输出功率的因素。在变频调速系统中，电机输出功率是为了匹配负载需求的，能跟随负载状况的改变而变化。把电动机实际输出功率与电动机额定功率之比称为电机带负载率β：

β=P/Pe

(9)

式中：P为电动机实际输出功率，W；Pe为电动机额定功率，W。

由式(7)可得，f和s影响电机带负载能力。由于s很小，工程实际应用经验表明：1-s可以近似为1。将式(9)代入式(8)并求解s，得到s关于f和负载率β的表达式：

(10)

式中：a1=CM·R2·k2;b1=p·Pe。

在异步电动机变频调速过程中，供电频率和电机带负载率是影响电机转差率的2个主要因素，即影响电机调速过程中转速-频率映射关系精准度的因素。因此，f和带负载率β成为量化s的2个重要指标。基于转差率回归方程量化方法，电机实际转速n的计算公式可表示为[11]

n=60/p[-1.934 1×10-4f2+(0.993 7-0.041 3β)f]

(11)

图3、图4为该模型预测电机输出转速的方法和传统比例定律确定转速的方式同实验测量结果对比。

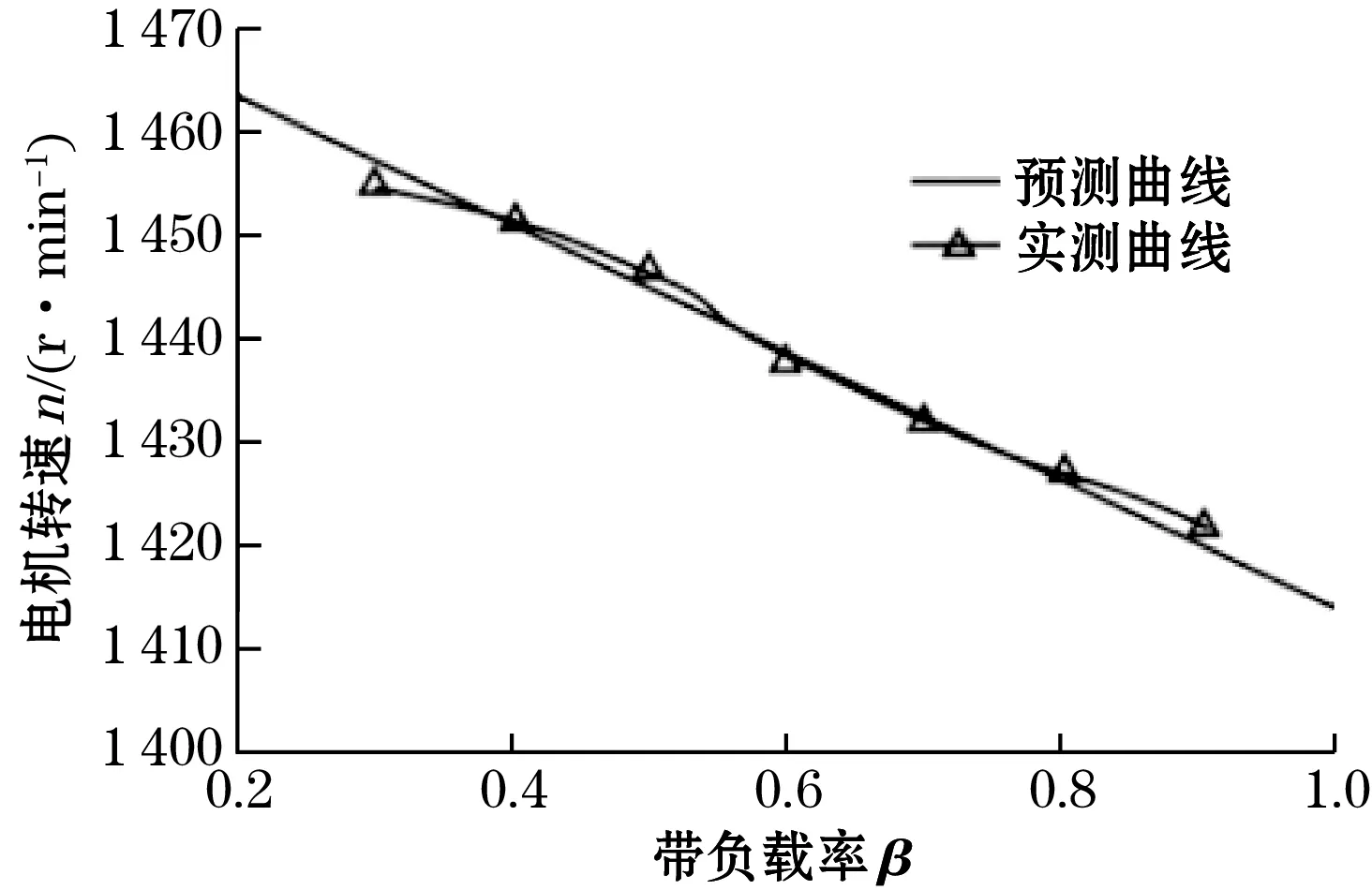
图3 50 Hz时电机转速-负载率预测曲线与离散点实测曲线对比

图4 负载率为1.0时电机转速-频率预测曲线与离散点实测曲线对比

由图3、图4可以看出，转速预测方法的精准性优于比例定律，且与实验测量误差在0.5%以内，电机带负载率在(0.6～0.8)时预测效果更佳。该方法克服了电动机变频调速过程中输出转速与预期转速误差大以及传统的控制过程复杂等问题，为后续电动机其他参变量的精准控制提供了经验参考。

2 清洗架同步运动模型

清洗架同步运动模型如图5所示。由图5 可知，当支架长度Le足够长且偏移角θ较小时，上、下行电机水平位移差S可表达为

图5 清洗架上、下行电机运动示意

S=|ΔL1-ΔL2|=Le|sinθ2-sinθ1|≈Le|θ2-θ1|

(12)

d(θ2-θ1)/dS=1/Le→0

(13)

式中：Le为清洗架长度，m；S为上下位移差，m。

Le足够大时，S=0处存在θ2-θ1的最小值，上下电机倾角可由S控制。

Δ=v1·Δt=π·D/60×n1·Δt
ΔL2=v2·Δt=π·D/60×n2·Δt

(14)

式中：v1和v2分别为上、下行电机的水平移速，m/s；n1和n2分别为上下电机转速，r/min。

由式(11)、式(14)可得：

(15)

式中：β1与β2为上、下行电机负载率，取值范围为[0，1]；Δt为调频间隔，s。

系统输入f1和f2即可获得上、下行电机的位移调节量，进而改变清洗架倾角。

ΔL1-ΔL2=π·D/p[K·(f1-f2)-0.041 3J]·Δt

(16)

式中：

J=β1f1-β2f2

K=-1.934 1×10-4(f1+f2)+0.993 7

(17)

用于频率补偿时，式(6)可进行一定程度简化：

ΔL1-ΔL2=0.932 4×π·D/p(f1-f2)·Δt

(18)

模糊控制器根据θ及dθ/dt推出ΔL1-ΔL2，由式(18)得出f1-f2，再补偿至f2输入端。

3 频率补偿算法

模糊逻辑控制具有较好的鲁棒性和适应性，因此被广泛应用于非线性、模型不完全确定的系统中。由于倾角的控制与上、下行电机的频率及负载率均有关联，本系统还具备强耦合特征。除此之外，倾角的检测及通过串口对变频器的频率进行在线修正，分别会受到采样速度及通讯速度的影响，所以本系统还具备迟滞特征。针对上述问题，本文提出模糊逻辑控制的方法，通过模糊语言规则实时修正控制器输出的上、下行电机的位移量，来实现清洗架倾角控制。模糊逻辑控制器将倾角θ及其变化率dθ/dt作为输入变量，输出变量为上、下行电机的位移量 ΔL1-ΔL2，如图6 所示。

图6 模糊逻辑控制原理框图

为保证模糊逻辑控制器的控制性能和精度，将倾角变化量θ与变化率dθ/dt的模糊子集定义为 8 个语言变量：{负大(NB)，负中(NM)，负小(NS)，零负(NO)，零正(PO)，正小(PS)，正中(PM)，正大(PB) }，将ΔL1-ΔL2的模糊子集定义为5个语言变量：{负大(NB)，负小(NS)，零(ZO)，正小(PS)，正大(PB) }，具体如式(19)所示。

ΔL1-ΔL2={NB,NS,ZO,PS,PB}
θ={NB,NM,NS,NO,PO,PS,PM,PB}
dθ/dt={NB,NM,NS,NO,PO,PS,PM,PB}

(19)

定义输入、输出的隶属度函数均为三角形函数，其中倾角变化量θ的论域设定为[-1，1]，隶属度函数如图7 所示。

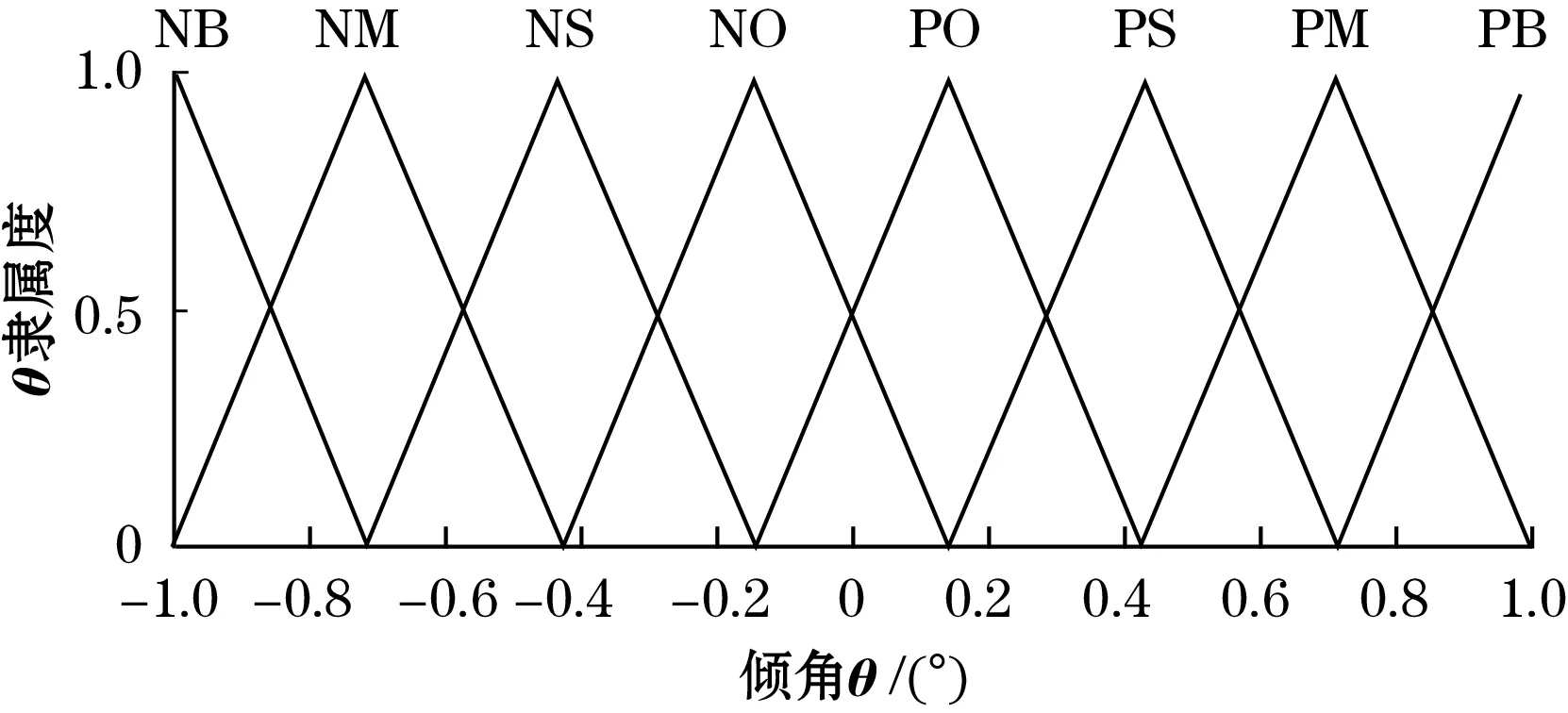
图7 θ隶属度函数

倾角变化率dθ/dt的论域设定为[-3，3]，隶属度函数如图8所示。

图8 dθ/dt隶属度函数

输出位移变化量ΔL1-ΔL2的论域设定为[-30，30]。具体隶属度函数如图9所示。

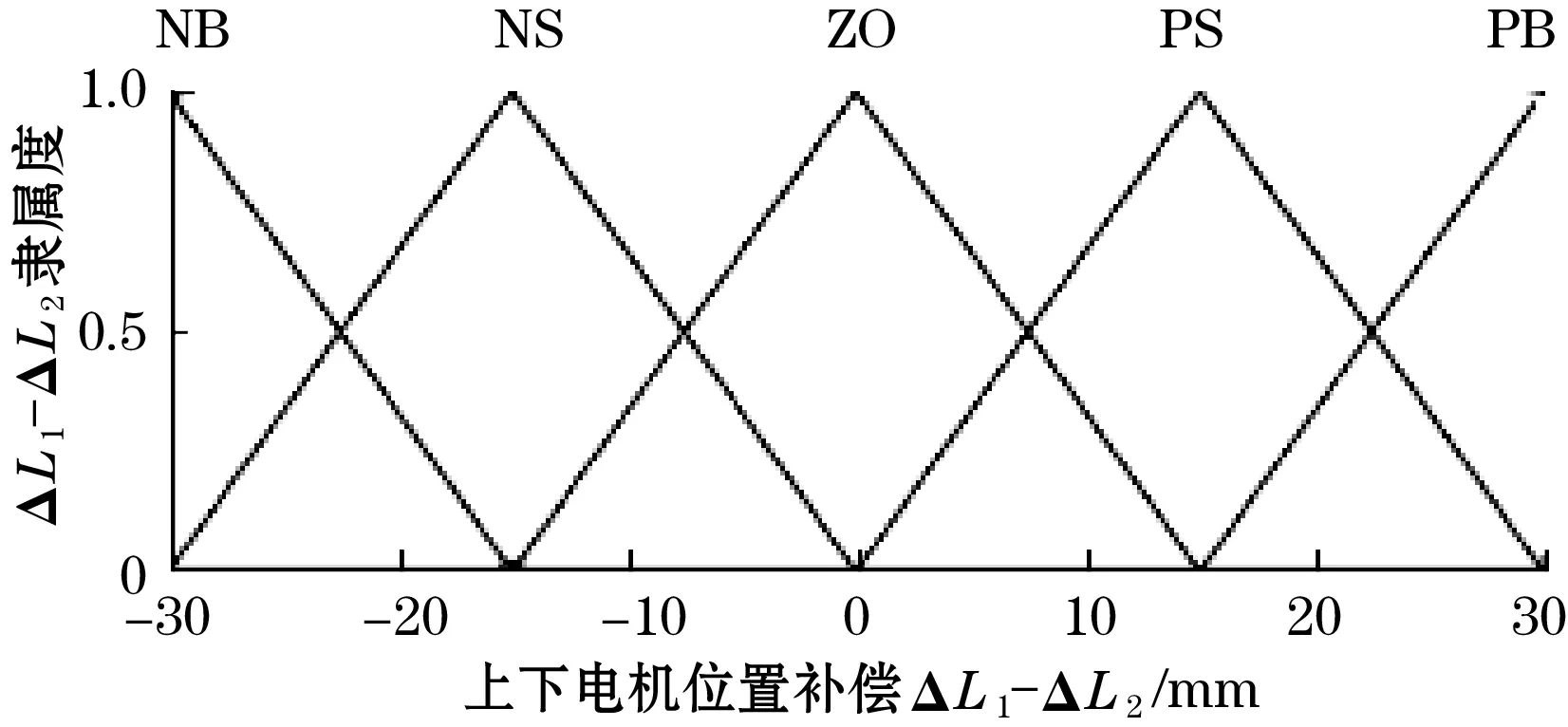
图9 ΔL1-ΔL2隶属度函数

模糊逻辑控制采用与扰动观察法相同的控制思路，将倾角值作为反馈信号，经过计算得到倾角增量与倾角变化率增量作为模糊逻辑控制器的输入变量。根据上述控制思想，可得到控制器设计原则，根据以下设计原则，采用IF A and B THEN C的语言规则，建立如表1所示的模糊逻辑规则如下。

(1)上一时刻倾角增量为正，倾角变化率为正，则输出反向位移变化量；

(2)上一时刻倾角增量为负，倾角变化率为负，则输出正向位移变化量；

(3)上一时刻倾角增量为正，倾角变化率为负，且前者主导，则输出反向位移变化量；

(4)上一时刻倾角增量为正，倾角变化率为负，且后者主导，则输出正向位移变化量；

(5)上一时刻倾角增量为负，倾角变化率为正，且前者主导，则输出正向位移变化量；

(6)上一时刻倾角增量为负，倾角变化率为正，且后者主导，则输出负向位移变化量；

(7)定义倾角增量比倾角变化率优先度高一阶，例如倾角增量正中等效于倾角变化率负大;

(8)倾角增量为正大或者负大时，无论倾角变化率如何，输出位移变化量的方向由前者决定，防止系统发生不稳定的情况，在倾角增量为零正或零负时，倾角变化率占主导，以快速达到稳定工作点。

模糊控制器采用Mamdani法则作为推理方法，采用重心法实现模糊子集的去模糊化。根据上述模糊逻辑规则表和推理法则，可得到模糊逻辑控制器输出特性曲面如图10所示。

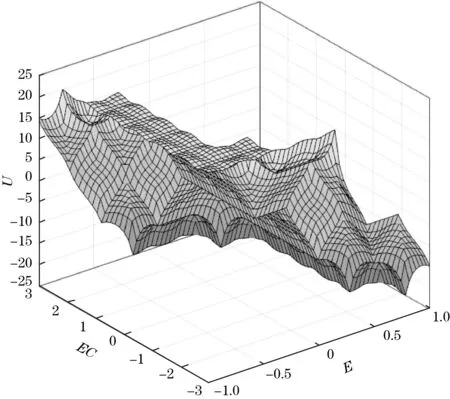
图10 模糊逻辑控制器输出曲面

模糊逻辑规则表如表1所示，表1中θeq是倾角变化率dθ/dt的等效变换，变换原理遵循语言规则(8)。

表1 模糊逻辑规则表

4 仿真分析

仿真系统整体示意如图11所示，角度扰动选取[-1,1]范围的正弦信号，模拟现场清洗架周而复始运动时的倾角扰动。上、下行电机的工作频率由step函数设定为25 Hz，由于变频器恒转矩下工作频率一般为5～50 Hz，故频率补偿范围为-20～25 Hz。在文献[3]中提及交叉耦合结构基础之上做了改进，本文频率补偿只针对上行电机，下行电机频率恒定。

图11 仿真系统整体示意图

(a)Fuzzy控制器

如图13所示，从倾角误差来看，PID和Fuzzy控制器均能取得较好的效果，针对[-1，1]的扰动角度，稳态误差峰值均低于±0.3°，峰值发生在θc与θr*过零点附近，对系统影响较小。梯长L越长，根据式(13)可知系统稳定点越理想，即倾角过零点处振荡峰峰值越低；此外，PID建立稳定时间较长，而Fuzzy控制器可以瞬时建立稳定状态，然而Fuzzy控制器输出幅值更低，相比PID控制器，其系统调频范围可以进一步增加。

图14中，首先将频率给定fin设为固定的25 Hz，即为上、下行电机的初始工作频率。扰动角度θr决定频率补偿fc，与文献[3]提出的交叉耦合系统不同的是，频率补偿fc仅对上行电机起作用，下行电机始终保持恒定。其中角度扰动来自于倾角传感器，确保系统的稳定性。而频率设定以25 Hz为中心上下调整时，可调整的幅度与控制器的响应速度及调节裕量有关。

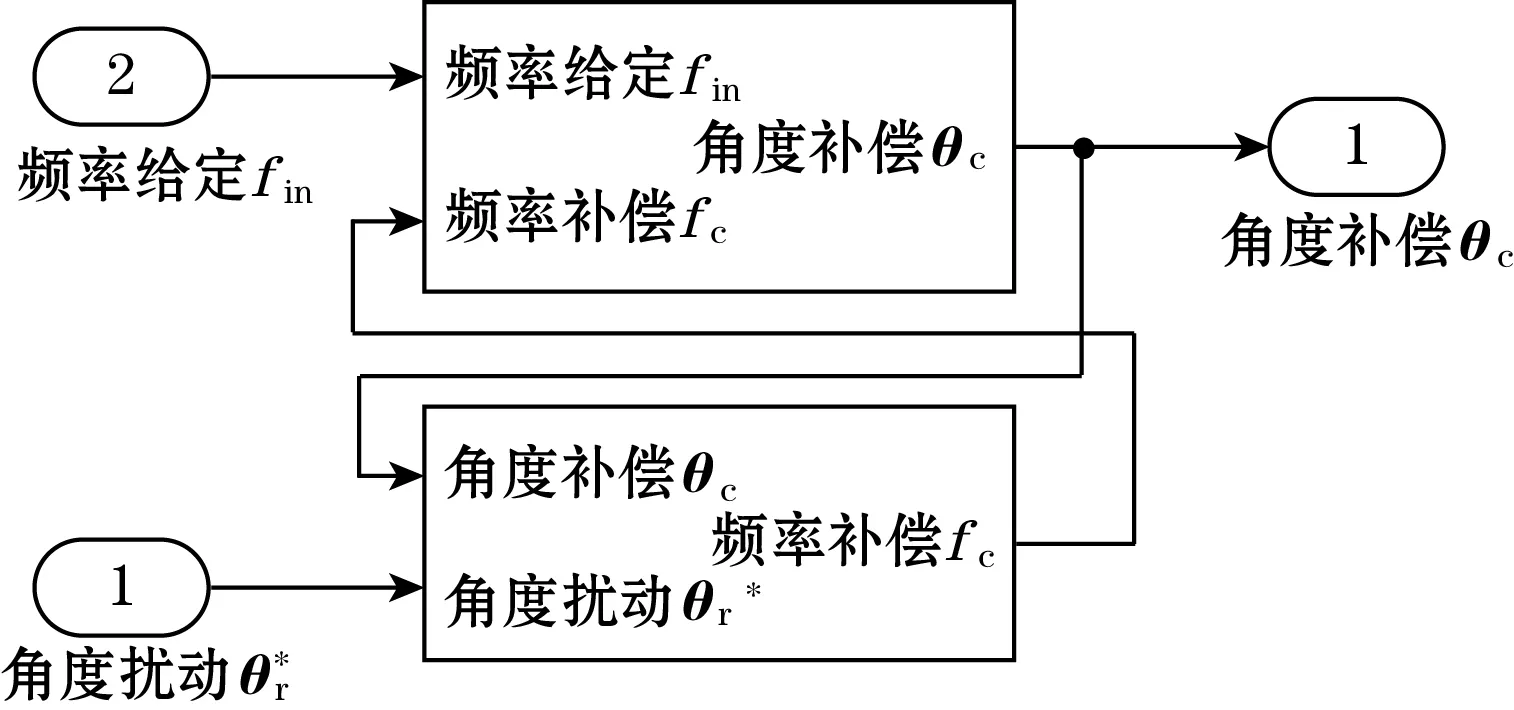
图14 子系统间逻辑示意图

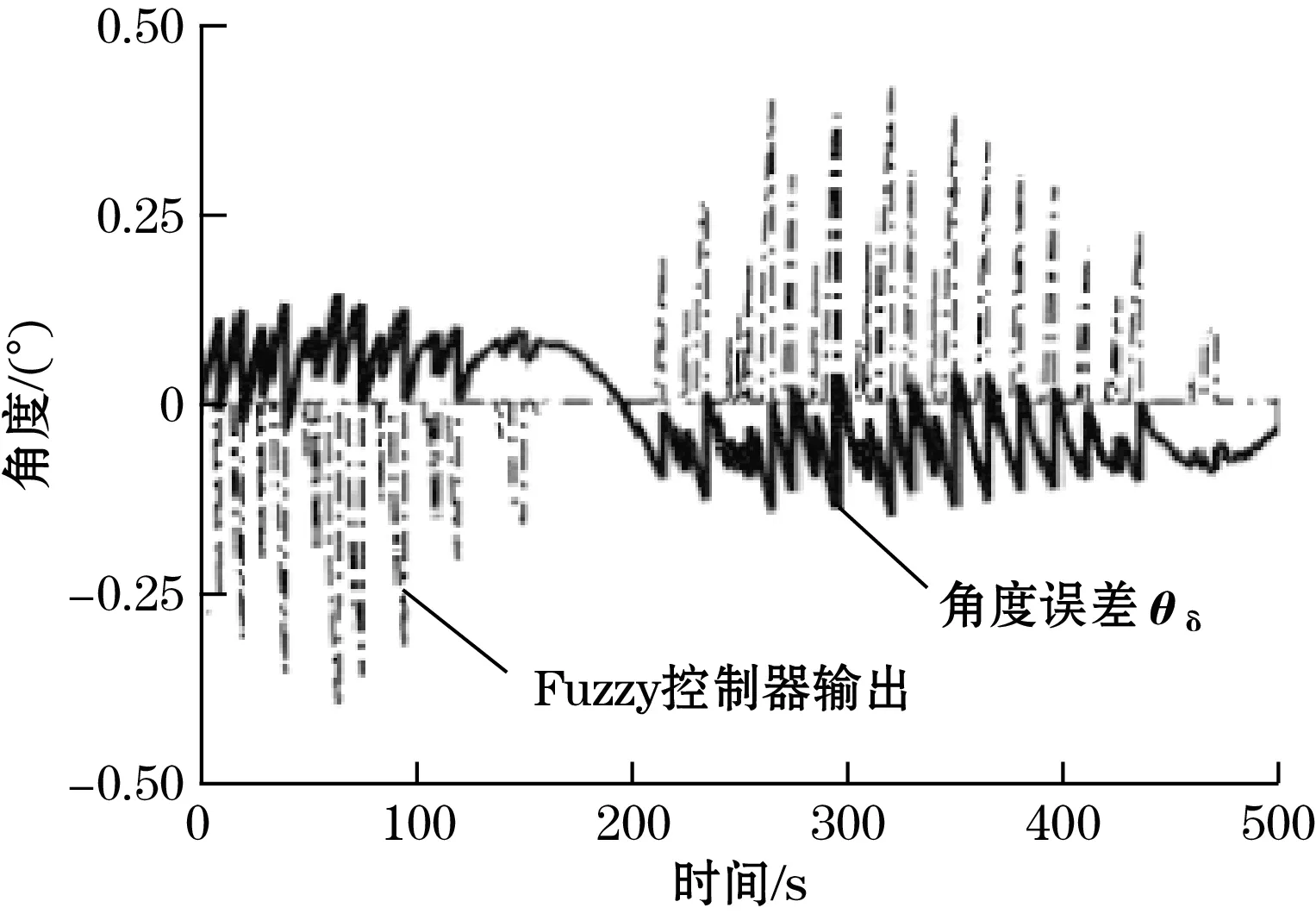
(a)角度误差和Fuzzy控制器输出

由图14、图16 所示，实际工程中，实时输入信号只有倾角传感器的角度信号，相当于角度扰动θr，角度补偿子系统的实时输入fc及输出θc只是过程量，针对某一时刻的角度扰动θr*，经过若干周期，最终将角度调整至模糊控制器“误差零点(ZO)”处。所以模型中频率限制范围为[5，50]，该频率区间一般对应恒转矩模式，相应感应电机机械特性曲线较“硬”，适合加减速及时变负载率情况的同步控制。

(a)Fuzzy子系统仿真模型

图16 角度补偿子系统仿真模型

如图17所示，经过限幅后的补偿频率fc为[-20，25]的一系列脉冲，对应上行电机工作频率在[5，50]之间调整。从补偿频率包络线来看，Fuzzy和PID控制器均能对图13 所示的角度误差做出准确的控制。相比PID控制器，Fuzzy控制器频率补偿曲线明显更稀疏。

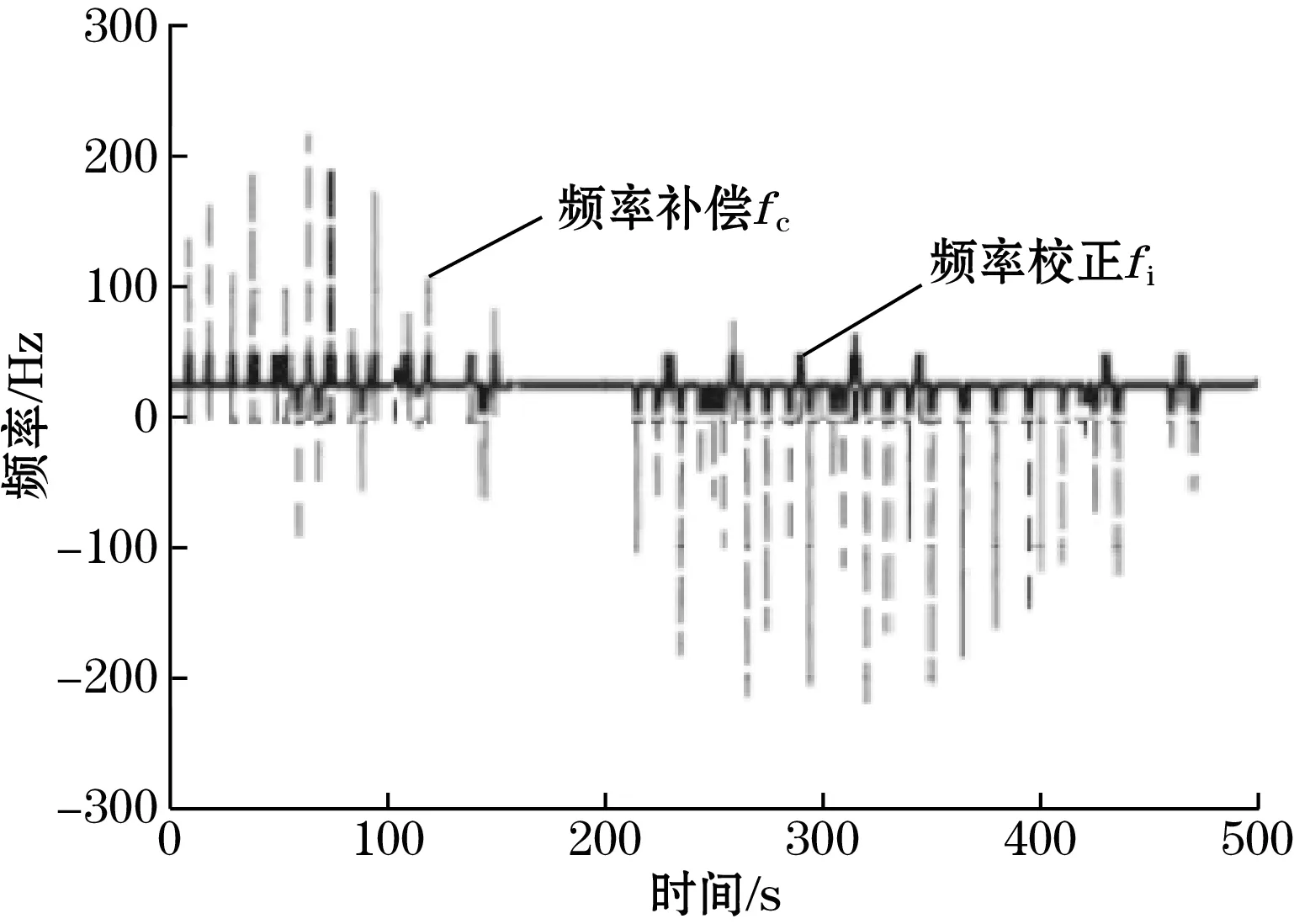
(a)Fuzzy控制器

为进一步比较Fuzzy和PID控制器的性能，将图14中用于位移累积的T0零阶保持器由5 s变更为2 s，如图17所示，PID控制器的变频周期与T0周期完全吻合。

而Fuzzy控制器能够以更少的频率补偿完成倾角在线校正。在倾角过零点处附近，PID控制器的频率幅值不发生改变，而反观Fuzzy控制器，当倾角最大时，频率幅值直接拉向最低，并不会如同PID控制器那样依然上下改变；而倾角在过零点附近时，和PID规则正好相反，Fuzzy变频效果明显。

5 结论

本文提出一种基于模糊逻辑控制的同步变频控制算法。在系统建模的基础上，分析上、下行电机位移与扰动角度之间的对应关系，根据感应电机机械特性，得出转速对频率及负载率的函数关系，建立系统模型，确定了系统控制策略。通过Simulink仿真，验证控制策略的可行性。对基于模糊逻辑控制的同步变频控制算法，通过分析得到以下结论。

(1)采用模糊逻辑控制算法，系统响应快速，且随控制器规则库增加，稳态误差有调整空间；

(2)采用模糊逻辑控制算法的系统，能够对扰动角度及其变化方向做出相对准确判断并快速调整，在扰动角度最大处及过零处，能够产生更合理的控制方式，有良好的鲁棒性和适应性。

(3)本文所提出的控制算法结构简单，检测参数少，对硬件电路要求较低，算法易于实现。在实现系统同步调节的前提下，提高了系统的响应速度，提升了稳定性。对大、中型变频调速系统的进一步复杂控制提供了借鉴。