基于改进DPC的多模型软测量建模方法及其应用

刘康康，戴 鹏，孙顺远

(1.江南大学物联网工程学院，江苏无锡 214000；2.山东东润仪表科技股份有限公司，山东烟台 264010)

0 引言

工业生产过程的复杂程度正在日益增加，通常存在多工况、非线性和时变性等特征，其相应的计算机控制系统也在不断地丰富和完善，同时推动了基于数据驱动理论软测量技术的发展[1]。针对实际的工业生产过程，建立单一软测量模型难以反映不同工况的特性，模型精度不能满足系统的要求，而多模型建模方法[2]能够更好地描述对象的复杂特性，提高模型精度和泛化能力。

在多模型建模过程中，将建模数据样本点进行准确聚类是保证所建模型预测性能的前提[3]。聚类分析是在对数据不进行任何假设的条件下，采用数学方法研究和处理所给对象的分类及各类之间亲疏程度[4]。常用的聚类算法如K均值聚类[5]、模糊C均值聚类[6]，需要人为设定聚类的数量，需要对数据有一定的先验知识。密度峰值聚类(density peaks clustering，DPC)算法是A. Rodriguez和A. Laio[7]提出的一种新型聚类算法。该算法无需预先给定聚类数目和初始聚类中心，自动给出样本的聚类中心，而且对数据集样本的形状没有严苛的要求，对任意形状的数据集样本都能实现高效的聚类。然而DPC算法也存在缺陷：局部密度的计算受截断距离影响，截断距离由人为设定，另外局部密度的不同计算方式也取决于数据集大小；剩余点的分配策略会产生多米诺效应，一旦一个局部密度较大的点类簇分配错误，可造成连环的分配错误。另一方面，在多模型软测量建模的最终预测输出时，需要对各个子模型的预测值进行组合。常见的组合方式主要有2种：开关切换方式和加权融合方式。其中，开关切换方式只是选择新来样本最有可能属于某个类簇模型进行预测输出，难以准确对全局模型进行描述，而加权融合方式可以根据新来的样本计算其隶属于某个子模型的概率，融合各个子模型的预测值得到比较准确的最终预测输出。因此，加权融合方式在实际建模过程中得到了广泛的研究与应用。

本文提出一种基于改进DPC的多模型软测量建模方法。首先，采用K近邻算法计算局部密度，避免截断距离人为选择的不足和局部密度计算方式受数据集大小的影响，并用K近邻算法和加权K近邻算法改进剩余点分配策略，避免连环的分配错误，划分得到更优的子数据集；然后，建立各个高斯过程回归(Gaussian process regression，GPR)子模型；最后，利用基于子模型预测性能并结合即时学习自适应地计算出新来样本隶属于各个子模型的后验概率，以此为权值融合各个GPR子模型的预测值得到最终输出，从而实现对一些复杂工业过程中的关键变量准确预测。

1 改进密度峰值聚类算法

1.1 密度峰值聚类算法

DPC算法是一种基于距离和密度的聚类算法，只需计算各个样本点之间的距离，具有速度快、精度高的特点。并且不需要人为给定聚类数目，适合工业生产过程中多工况、变量多等特点。理想的聚类中心应该有如下特点：它们被具有相对较低局部密度的邻居数据点包围着；它们与更高局部密度的数据点具有相对较大的距离。为了寻找理想的聚类中心，DPC算法引入数据点i的局部密度ρi和数据点i到具有更高局部密度点j之间的最短距离δi。

局部密度ρi定义为

(1)

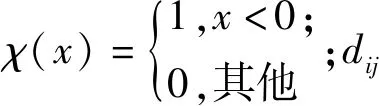
对于“小”数据集，难以对局部密度进行可靠计算，DPC算法采用高斯核函数计算ρi，表达式为

(2)

距离δi定义如下：

(3)

对于局部密度最大的点，有

(4)

DPC算法的核心是引入决策图来获取聚类中心，决策图建立在二维坐标系下，局部密度ρi为横坐标，距离δi为纵坐标，选择ρi、δi都较大的点作为聚类中心，即决策图右上方的数据点。确定聚类中心后，将剩余数据点分配到密度比其大且距其最近的类簇。

1.2 改进的密度峰值聚类算法

DPC算法能够简单高效地处理聚类问题，但却存在如下不足：

(1)局部密度计算有不同的方法，根据经验，“大”数据集采用式(1)，“小”数据集采用式(2)，然而对于数据集大小的划分没有标准，使用不同公式产生的聚类结果不同。此外2个公式中都有人为设定的截断距离，特别对于较小的数据集受截断距离影响较大。

(2)剩余点的分配策略可能会导致错误的传播，一旦一个局部密度较大的点类簇分配错误，可造成其周围局部密度较低的数据点分配连环错误。改进的DPC算法采用K近邻算法计算局部密度，并用K近邻算法和加权K近邻算法改进剩余点分配策略。

K近邻分类算法本质可以看作是对每一个测试数据找到其在训练数据中的k个邻近，并将这k个邻近中频率出现最高的类别作为该测试数据的类别。假设样本有标签可为Label=1,2,…，C，K近邻算法在数据点i的分类公式如下：

(5)

式中δ为克罗内克函数。

在传统的K近邻算法中，认为数据点的k个近邻是等权的，然而在实际意义中，各个k近邻对测试样本标签的贡献程度不同，贡献程度与特征距离有关。提出了加权K近邻算法如下：

(6)

改进的DPC算法采用K近邻算法重新定义了局部密度ρi的表达式：

(7)

该定义保证局部密度计算只与该数据点k近邻的分布有关，即独立于数据集的大小，又避免了人为选取截断距离经验的不足。

改进的分配策略先使用K近邻算法直接将聚类中心的标签直接传播到k个近邻定义如下：

(8)

式中peakj为j的聚类中心。

再使用加权K近邻算法分配还未分配的剩余点，定义权值wij如下：

(9)

考虑使用加权K近邻算法，可能存在数据点i的k个近邻可能存在未被分配，先找到还未被分配数据点中k个近邻已被分配标签最多的数据点，再使用加权K近邻算法提出的分配标签公式：

(10)

式中Label≠∅为该数据点已经被分配标签。

设输入：数据集为X，参数为k，输出：已标记聚类类别的数据集。改进的DPC算法实现步骤：

(1)对数据集数据作归一化预处理。

(2)采用K近邻算法重新定义的式(7)计算局部密度ρi，使用式(3)或式(4)计算距离δi。

(3)通过局部密度ρi和距离δi绘制决策图，获取聚类中心并标记标签为Label=1，2，…,C。

(4)使用式(8)将聚类中心的标签直接传播到k个近邻。

(5)找出还未被分配数据点中k个近邻已被分配标签最多的数据点，使用式(10)进行分配标签。

(6)若还有未被分配标签数据点，转至步骤(5)直至所有数据点都有标签，得到已标聚类类别的数据集。

2 多模型建模和融合方法

2.1 高斯过程回归

(11)

cov(f*)=K(x*,x*)-K(x*,X)C-1K(X，x*)

(12)

(13)

高斯过程回归中协方差矩阵是通过协方差函数确定，通常使用平方指数协方差函数：

(14)

(15)

2.2 基于子模型预测性能的贝叶斯自适应融合算法

为了得到最终的预测输出，需要融合各个子模型的预测值，因此，子模型的权值计算方法对软测量模型的精度至关重要。传统方法中，子模型的权值一般通过新来样本到各个子数据集聚类中心的距离计算得到[10]。近几年，基于子模型的预测能力或者预测值的不确定性计算后验概率的方法得到广泛应用[11]。

利用改进的DPC算法将训练样本划分为C个子数据集，并用GPR方法建立子模型分别为LMc,c=1,2，C。对于新样本xnew，基于贝叶斯定理得到最终的预测输出表示为

(16)

由贝叶斯定理可知，后验概率的计算公式如下：

(17)

式中：P(LMc)为第c个子模型的先验概率；P(xnew|LMc)为xnew隶属于第c个子模型的条件概率。

若子模型的先验概率和xnew隶属于该子模型的条件概率越大，则该子模型对xnew具有更准确的输出，基于此关系结合实时学习(just-in-time learning，JITL)[12]的思路，提出一种基于基于子模型预测性能的贝叶斯自适应融合算法。对于新来的样本，通过欧氏距离的相似度准则，在训练样本中找出与之相似度最大的Ns个样本构成相似样本集，并相应的计算在各个子模型中的均方根误差公式为

(18)

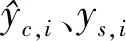
RMSEc反映了第c个子模型对相似样本集的预测性能，同时也反映了对新来样本的预测能力。因此，新来样本隶属于第c个子模型的条件概率P(xnew|LMc)可以定义为

(19)

同时第c个子模型的先验概率P(LMc)定义为

(20)

式中Ns,c为相似样本集在第c个子数据集中的个数。

对于新来的样本使用式(19)和式(20)分别计算各个子模型的条件概率和先验概率，在代入式(17)求出相应的后验概率，最终根据式(16)融合各个子模型的预测值得到最终预测输出。

3 基于改进DPC的多模型软测量建模步骤

本文提出的基于改进DPC的多模型软测量建模流程如图1所示。

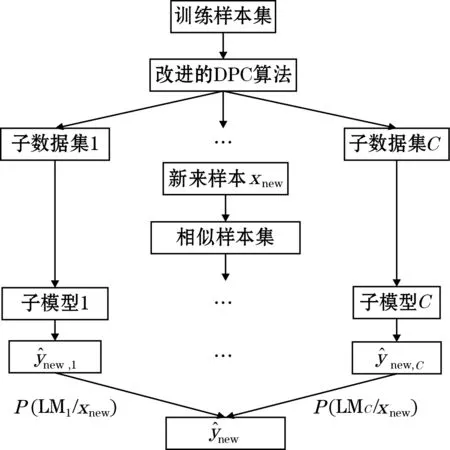
图1 基于改进DPC的多模型软测量建模

具体的执行步骤如下：

(1)利用改进的DPC算法对原始训练集进行聚类，得到C个子数据集。

(2)用GPR方法对子数据集建立各个子模型。

(3)对于新来样本预测各个子模型的输出值，并用基于子模型预测性能的贝叶斯融合自适应算法计算出新来样本隶属于各个子模型的后验概率。

(4)利用式(16)融合各个子模型的预测值得到最终预测输出。

4 仿真研究

4.1 标准数据的聚类仿真

选取6个UCI真实数据集对改进的DPC算法进行测试与评价，并与DPC、AP[3]、DBSCAN[13]、K-means的仿真结果进行对比，其中因为K-means算法选取初始聚类中心和聚类数目都具有随机性，所以本文采用20次重复实验的平均值作为其最终的仿真结果。本文选用的UCI真实数据集如表1所示。

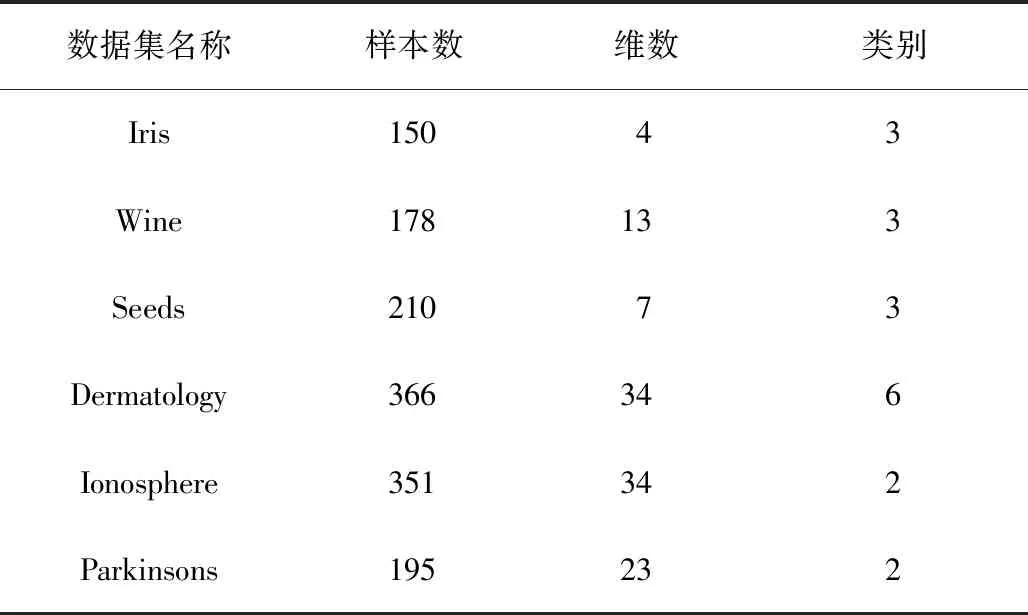
表1 本文选取的UCI数据集

采用聚类准确率(Acc)、调整的Rand指数(adjusted rand index，ARI)作为度量指标来对仿真结果进行评价。这两种指标作为最常用的评判聚类质量的指标，值越大说明聚类效果越好。

上述5个聚类算法6个UCI数据集上的聚类结果指标如表2所示。其中Par表示算法中所用的参数，加框的表示最优。

从表2可以看出，本文提出改进DPC算法的聚类指标都优于DPC、AP、DBSCAN、K-means，说明了改进的DPC算法进行聚类更加符合真实的类簇归属情况。另外当选取的聚类中心相同时，如在Seeds数据集改进的DPC算法和DPC算法都是取第29、92、183样本点作为聚类中心，但是聚类指标优于DPC算法，表明本文提出改进的分配策略在分配剩余数据点时更准确。

表2 UCI数据集在各个算法的评价指标

4.2 SRU软测量建模

为了验证本文所提软测量建模方法的有效性，对硫回收装置(sulfur recovery unit，SRU)中H2S浓度进行软测量建模。SRU装置用于含硫气体排入大气前硫的回收，以此来保护生态环境，其装置如图2所示。其装置主要处理酸性气体：一种是H2S气体(也称MEA气体)，另一种为来自含硫污水汽提设备(SWS)的气体，其中富含H2S、NH3气体(也称为SWS气体)。主要燃烧室在具有充足空气(AIR_MEA)时充分燃烧MEA气体，另一个燃烧室用于处理SWS气体，其进入的空气AIR_SWS[14]。其过程与H2S浓度有关的5个变量作为辅助变量用于软测量建模。从SRU装置过程数据中选取1 200组数据，其中2/3作为训练集，1/3作为测试集。

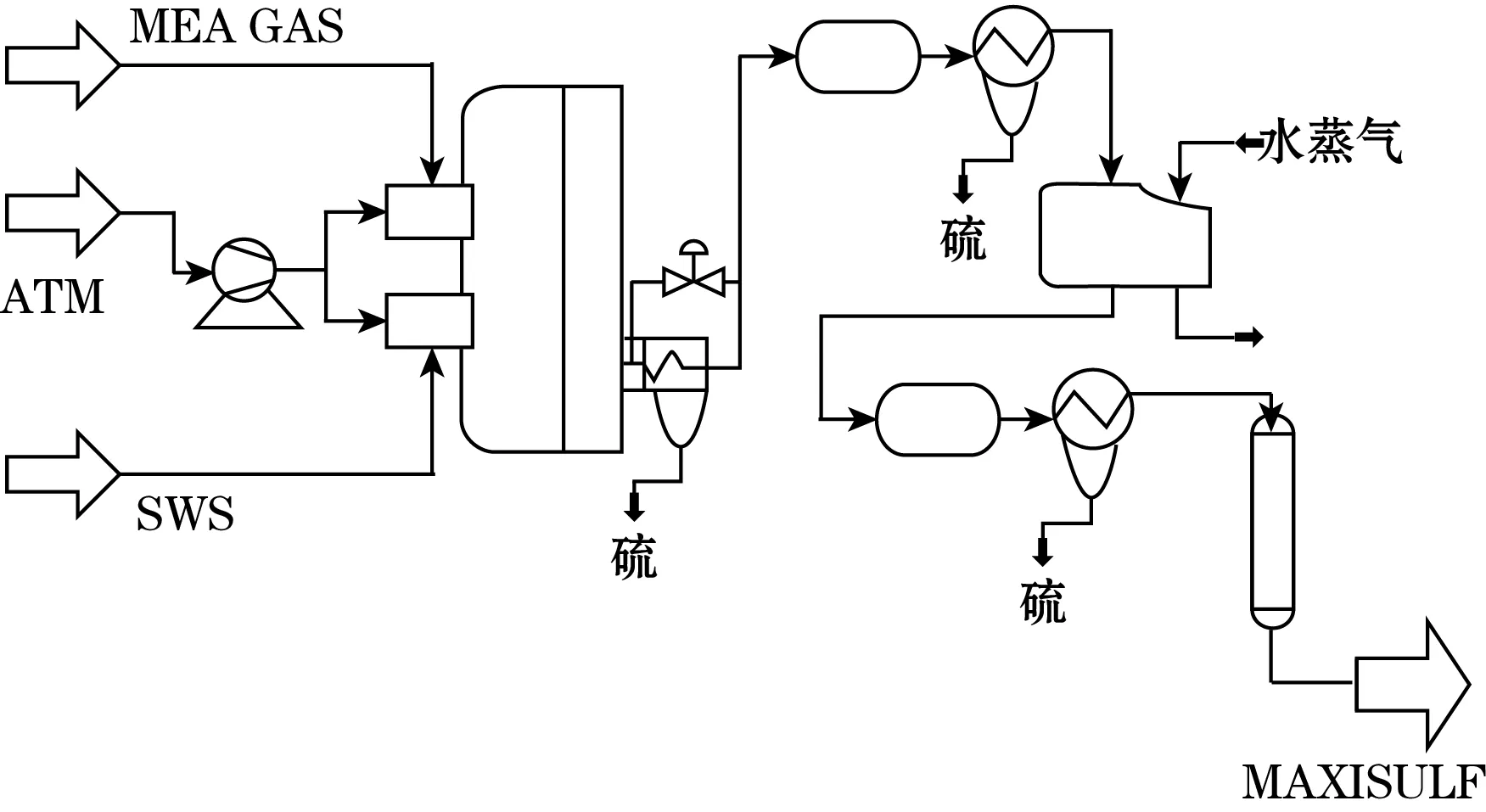
图2 硫回收装置

为了进一步对比分析本文所提建模方法的预测性能，将不同的聚类方法和融合方式进行组合。方法1为DPC-GPR-Bayesian方法，方法2为改进的DPC-GPR-开关切换(即新测试样本，到聚类中心最近的子模型对当前样本预测输出)，方法3为本文提出的方法即改进的DPC-GPR-bayesian。使用均方根误差(RMSE)和跟踪性能指标(TP)作为模型的性能评价指标：

(21)

(22)

图3为改进的DPC算法和DPC算法对SRU数据训练样本聚类的决策图。

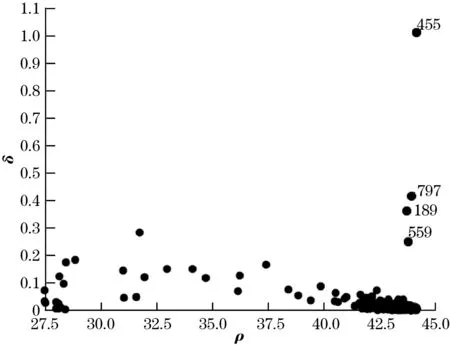
(a)改进的DPC算法决策图

改进的DPC算法参数k为45，DPC算法的参数为2(即dc取所有数据点的相互距离dij(i,j=1,2，…,n；i≠j)由小到大排序后2%位置的数值)。从图3可以看出，2种算法都取4个聚类中心，但聚类中心不同，改进的DPC算法选取第455、797、189、559样本点作为聚类中心，每类个数分别为339、254、69、14，DPC算法选取第91、797、189、588样本点作为聚类中心，每类个数分别为343、251、69、141。使用Silhouette[15]指标对2个聚类算法进行评价，指标值越大说明类内紧密程度越高，类间可分性越大，即聚类效果越好。改进的DPC算法Silhouette指标为0.731 3，优于DPC算法的0.730 1，说明在SRU数据上改进的DPC算法聚类效果优于DPC算法。

图4为3种软测量方法对SRU装置中的H2S浓度的预测值和真实值对比曲线，可以看出，方法2的预测效果较差，跟踪能力较弱，方法1和方法3的预测效果相近，预测效果比较好，跟踪性能更强。

(a)DPC-GPR-Bayesian方法预测结果

表3为3种方法预测结果的性能指标。

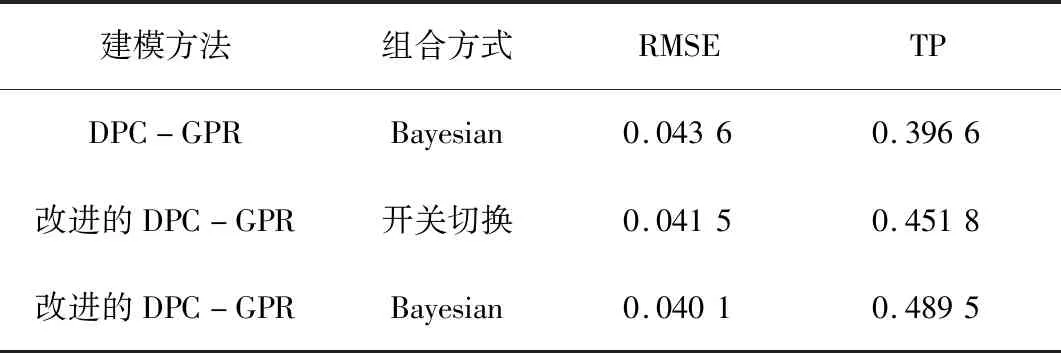
表3 不同建模方法的性能指标

图5为3种软测量建模方法对SRU装置中H2S浓度的预测的误差图。通过对比表3和图5可以看出，相对于开关切换方式，基于子模型预测性能的贝叶斯自适应融合方法可以有效地计算新来样本隶属各个子模型的权值，得到更加准确的预测值。相对于DPC算法，改进的DPC算法得到的子数据集具有较好的聚类结构，使得所建模型的预测结果更好。对于RMSE和TP指标，本文方法建立模型的预测误差均比其他方法更佳，能够对SRU装置中H2S浓度进行有效预测。

图5 H2S浓度预测的误差

5 结束语

针对具有多工况、非线性的复杂工业生产过程，本文提出了基于改进密度峰值聚类的多模型软测量建模方法。利用K近邻算法和加权K近邻算法对DPC算法进行改进，避免截断距离人为选择的不足和局部密度计算方式受数据集大小的影响，并解决了剩余点分配连环错误的问题；同时，利用基于子模型预测性能并结合即时学习自适应地计算出新样本隶属于各个子模型的后验概率，以此为权值融合各个GPR子模型，最终得到较准确的预测结果。仿真结果表明，本文提出的建模方法取得较好的预测效果。